1.2 Flash distillation
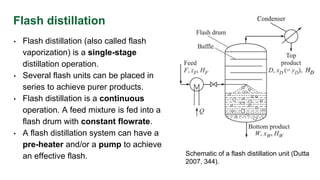
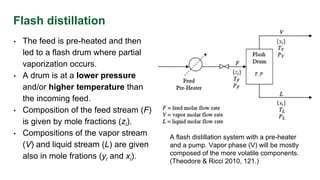
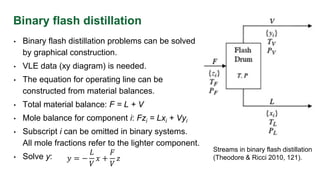
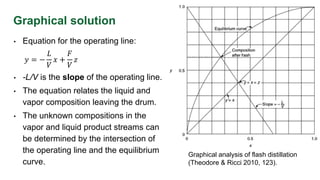
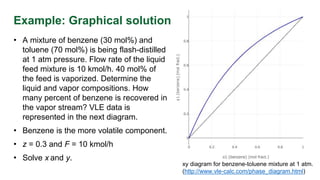
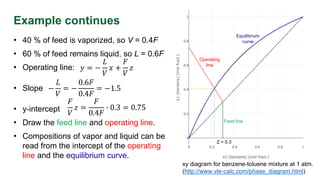
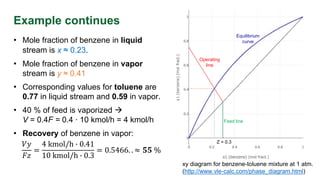
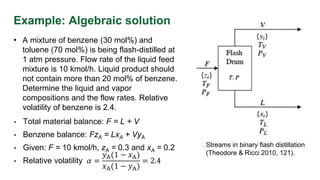
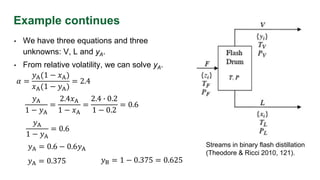
The document discusses flash distillation, a continuous distillation process involving partial vaporization, typically of feed mixtures. It covers both binary and multicomponent flash distillation, including calculations for vapor and liquid compositions and recovery rates using material balances and graphical methods. Additionally, it references key literature and educational videos for further understanding of the process.
More Related Content
Similar to 1.2 Flash distillation
More from South-Eastern Finland University of Applied Sciences
1.2 Flash distillation
- 1. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. Flash distillation
- 2. Flash distillation • Flashdistillation (also called flash vaporization) is a single-stage distillation operation. • Several flash units can be placed in series to achieve purer products. • Flash distillation is a continuous operation. A feed mixture is fed into a flash drum with constant flowrate. • A flash distillation system can have a pre-heater and/or a pump to achieve an effective flash. Schematic of a flash distillation unit (Dutta 2007, 344).
- 3. Flash distillation • Thefeed is pre-heated and then led to a flash drum where partial vaporization occurs. • A drum is at a lower pressure and/or higher temperature than the incoming feed. • Composition of the feed stream (F) is given by mole fractions (zi). • Compositions of the vapor stream (V) and liquid stream (L) are given also in mole frations (yi and xi). A flash distillation system with a pre-heater and a pump. Vapor phase (V) will be mostly composed of the more volatile components. (Theodore & Ricci 2010, 121.)
- 4. Binary flash distillation •Binary flash distillation problems can be solved by graphical construction. • VLE data (xy diagram) is needed. • The equation for operating line can be constructed from material balances. • Total material balance: F = L + V • Mole balance for component i: Fzi = Lxi + Vyi • Subscript i can be omitted in binary systems. All mole fractions refer to the lighter component. • Solve y: Streams in binary flash distillation (Theodore & Ricci 2010, 121). 𝑦 = − 𝐿 𝑉 𝑥 + 𝐹 𝑉 𝑧
- 5. Graphical solution • Equationfor the operating line: Graphical analysis of flash distillation (Theodore & Ricci 2010, 123). 𝑦 = − 𝐿 𝑉 𝑥 + 𝐹 𝑉 𝑧 • -L/V is the slope of the operating line. • The equation relates the liquid and vapor composition leaving the drum. • The unknown compositions in the vapor and liquid product streams can be determined by the intersection of the operating line and the equilibrium curve.
- 6. Example: Graphical solution •A mixture of benzene (30 mol%) and toluene (70 mol%) is being flash-distilled at 1 atm pressure. Flow rate of the liquid feed mixture is 10 kmol/h. 40 mol% of the feed is vaporized. Determine the liquid and vapor compositions. How many percent of benzene is recovered in the vapor stream? VLE data is represented in the next diagram. • Benzene is the more volatile component. • z = 0.3 and F = 10 kmol/h • Solve x and y. xy diagram for benzene-toluene mixture at 1 atm. (http://www.vle-calc.com/phase_diagram.html)
- 7. Example continues • 40% of feed is vaporized, so V = 0.4F • 60 % of feed remains liquid, so L = 0.6F • Operating line: • Slope • y-intercept • Draw the feed line and operating line. • Compositions of vapor and liquid can be read from the intercept of the operating line and the equilibrium curve. 𝑦 = − 𝐿 𝑉 𝑥 + 𝐹 𝑉 𝑧 xy diagram for benzene-toluene mixture at 1 atm. (http://www.vle-calc.com/phase_diagram.html) − 𝐿 𝑉 = − 0.6𝐹 0.4𝐹 = −1.5 𝐹 𝑉 𝑧 = 𝐹 0.4𝐹 ∙ 0.3 = 0.75 Z = 0.3 Operating line Feed line Equilibrium curve
- 8. Example continues • Molefraction of benzene in liquid stream is x ≈ 0.23. • Mole fraction of benzene in vapor stream is y ≈ 0.41 • Corresponding values for toluene are 0.77 in liquid stream and 0.59 in vapor. • 40 % of feed is vaporized V = 0.4F = 0.4 ∙ 10 kmol/h = 4 kmol/h • Recovery of benzene in vapor: xy diagram for benzene-toluene mixture at 1 atm. (http://www.vle-calc.com/phase_diagram.html) Z = 0.3 Operating line Feed line Equilibrium curve 𝑉𝑦 𝐹𝑧 = 4 kmol/h ∙ 0.41 10 kmol/h ∙ 0.3 = 0.5466. . ≈ 𝟓𝟓 %
- 9. Example: Algebraic solution •A mixture of benzene (30 mol%) and toluene (70 mol%) is being flash-distilled at 1 atm pressure. Flow rate of the liquid feed mixture is 10 kmol/h. Liquid product should not contain more than 20 mol% of benzene. Determine the liquid and vapor compositions and the flow rates. Relative volatility of benzene is 2.4. • Total material balance: F = L + V • Benzene balance: FzA = LxA + VyA • Given: F = 10 kmol/h, zA = 0.3 and xA = 0.2 • Relative volatility Streams in binary flash distillation (Theodore & Ricci 2010, 121). 𝛼 = 𝑦A(1 − 𝑥A) 𝑥A(1 − 𝑦A) = 2.4
- 10. Example continues • Wehave three equations and three unknowns: V, L and yA. • From relative volatility, we can solve yA. Streams in binary flash distillation (Theodore & Ricci 2010, 121). 𝛼 = 𝑦A(1 − 𝑥A) 𝑥A(1 − 𝑦A) = 2.4 𝑦A 1 − 𝑦A = 2.4𝑥A 1 − 𝑥A = 2.4 ∙ 0.2 1 − 0.2 = 0.6 𝑦A 1 − 𝑦A = 0.6 𝑦A = 0.6 − 0.6𝑦A 𝑦A = 0.375 𝑦B = 1 − 0.375 = 0.625
- 11. Example continues • Frommaterial balances: • F = L + V L = F - V • FzA = (F - V)xA + VyA • Solve 𝑉 = 𝐹𝑧𝐴−𝐹𝑥𝐴 𝑦𝐴−𝑥𝐴 • F = 10 kmol/h, zA = 0.3, xA = 0.2, yA = 0.375 • 𝑉 = 𝐹𝑧𝐴−𝐹𝑥𝐴 𝑦𝐴−𝑥𝐴 = 10∙0.3−10∙0.2 0.375−0.2 = 5.714 … ≈ 5.71 kmol/h • L = F – V = 10 – 5.7 = 4.29 kmol/h • Flow rates in vapor: Benzene VyA ≈ 2.14 kmol/h and toluene VyB ≈ 3.57 kmol/h • Flow rates in liquid: Benzene LxA ≈ 0.86 kmol/h and toluene LxB ≈ 3.43 kmol/h Streams in binary flash distillation (Theodore & Ricci 2010, 121).
- 12. Multicomponent flash distillation •Multicomponent flash distillation problems require an iterative procedure. • So called Rachford-Rice equation is needed: • If the feed composition is known, this eaquation can be used for calculation of Ψ at a given flash temperature and pressure. • After that, the compositions of the liquid and vapor streams are calculated by utilizing material balances and the resulting equations: • One example can be found in the video: https://youtu.be/On5UqiHDRd4 (6:31) Ψ = V/F = molar fraction of feed which leaves as vapor Ki = phase equilibrium constant 𝑓 ψ = 𝑖=1 𝑛 𝑧𝑖(𝐾𝑖 − 1) 1 + (𝐾𝑖 − 1)ψ = 0 𝑦𝑖 = 𝑧𝑖𝐾𝑖 1 + (𝐾𝑖 − 1)ψ 𝑥𝑖 = 𝑧𝑖 1 + (𝐾𝑖 − 1)ψ
- 13. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. References Dutta, B. K. 2007. Principles of mass transfer and separation processes. New Delhi: Prentice-Hall, pp. 344-347. Theodore, L. & Ricci, F. 2010. Mass Transfer Operations for the Practicing Engineer. John Wiley & Sons, Inc, pp. 120-126. Videos: • An introduction to flash distillation: https://youtu.be/cac5J273dJQ (7:06) • Flash distillation derivation: https://youtu.be/m7ZN2cU9tZU (6:51) • Multicomponent flash distillation: https://youtu.be/On5UqiHDRd4 (6:31)