Convective mass transfer
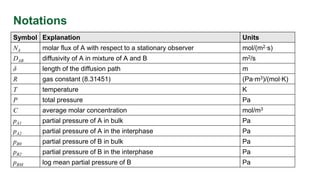
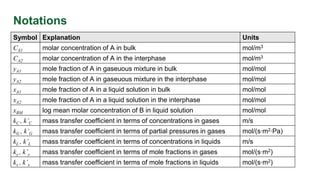
This document discusses convective mass transfer and mass transfer coefficients. It defines convective mass transfer as the rapid transfer of mass that occurs when there is motion in the transfer medium compared to the slower process of molecular diffusion. Mass transfer coefficients are introduced to simplify calculations of mass transfer rates. Different types of mass transfer coefficients are presented based on whether they are used for gases or liquids, and whether they are expressed in terms of concentrations, mole fractions, or partial pressures. Approximations for typical values of mass transfer coefficients in gas and liquid phases are provided.
More Related Content
![CHEE_220_Lecture_Fluidization_2021[1].pptx](https://cdn.slidesharecdn.com/ss_thumbnails/chee220lecturefluidization20211-230329153950-84712558-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Convective mass transfer
More from South-Eastern Finland University of Applied Sciences
Convective mass transfer
- 1. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. Convective mass transfer
- 2. Convective mass transfer •Molecular diffusion has a major role in a stagnant medium. It is extremely slow process. If there is motion in the medium, the rate of mass transfer increases dramatically. This is called convective mass transfer. • For example, if you add sugar in coffee, it will dissolve much more rapidly if you stir it with the spoon. • There is a ‘boundary layer’ or ‘film’ surrounding the sugar crystal which get saturated instantly. Dissolved sugar diffuses from the interface to the bulk through this ‘film’. Stirring decreases the thickness of the film and accelerates the rate of mass transfer.
- 3. Mass transfer coefficients •Theoretical calculations of the mass transfer rate in turbulent flow can become very complex. Mass transfer coefficients are here to simplify the calculations. • The idea of mass transfer coefficient is similar to heat transfer coefficient, although there are different types of mass transfer coefficients. • mass transfer in liquid or gas phase • choice of the driving force • equimolar counterdiffusion or diffusion of A through stagnant B • These are presented on the next slide. Heat transfer coefficient Mass transfer coefficient ℎ = 𝑞 ∆𝑇 𝑘𝑐 = 𝑁𝐴 ∆𝐶𝐴 q = heat flux ΔT = difference in temperature between the solid surface and surrounding area NA = molar flux ΔCA = difference in concentration between the interface and the bulk fluid Comparison of heat transfer coefficient and mass transfer coefficient
- 4. Different types ofmass transfer coefficients Equimolar counter diffusion Diffusion of A through non-diffusing B in G A S E S In terms of partial pressures In terms of mole fractions In terms of concentrations in L I Q U I D S In terms of concentrations In terms of mole fractions 𝑁𝐴 = 𝑘′𝐿 𝐶𝐴1 − 𝐶𝐴2 𝑁𝐴 = 𝑘′𝑥 𝑥𝐴1 − 𝑥𝐴2 𝑁𝐴 = 𝑘′𝑦 𝑦𝐴1 − 𝑦𝐴2 𝑁𝐴 = 𝑘′𝐺 𝑝𝐴1 − 𝑝𝐴2 𝑁𝐴 = 𝑘𝐿 𝐶𝐴1 − 𝐶𝐴2 𝑁𝐴 = 𝑘𝑥 𝑥𝐴1 − 𝑥𝐴2 𝑘𝐺 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝛿𝑝𝐵𝑀 𝑝𝐵𝑀 = 𝑝𝐵2 − 𝑝𝐵1 ln 𝑝𝐵2 𝑝𝐵1 𝑥𝐵𝑀 = 𝑥𝐵2 − 𝑥𝐵1 ln 𝑥𝐵2 𝑥𝐵1 𝑘′𝐺 = 𝐷𝐴𝐵 𝑅𝑇𝛿 𝑘′𝑦 = 𝐷𝐴𝐵𝑃 𝑅𝑇𝛿 𝑘′𝐿 = 𝐷𝐴𝐵 𝛿 𝑘′𝑥 = 𝐶𝐷𝐴𝐵 𝛿 𝑁𝐴 = 𝑘𝐺 𝑝𝐴1 − 𝑝𝐴2 𝑁𝐴 = 𝑘𝑦 𝑦𝐴1 − 𝑦𝐴2 𝑘𝑦 = 𝐷𝐴𝐵𝑃2 𝑅𝑇𝛿𝑝𝐵𝑀 𝑁𝐴 = 𝑘′𝑐 𝐶𝐴1 − 𝐶𝐴2 𝑘′𝐶 = 𝐷𝐴𝐵 𝛿 𝑁𝐴 = 𝑘𝑐 𝐶𝐴1 − 𝐶𝐴2 𝑘𝐶 = 𝐷𝐴𝐵𝑃 𝛿𝑝𝐵𝑀 𝑘𝐿 = 𝐷𝐴𝐵 𝛿𝑥𝐵𝑀 𝑘𝑥 = 𝐶𝐷𝐴𝐵 𝛿𝑥𝐵𝑀
- 5. Notations Symbol Explanation Units NAmolar flux of A with respect to a stationary observer mol/(m2∙s) DAB diffusivity of A in mixture of A and B m2/s δ length of the diffusion path m R gas constant (8.31451) (Pa∙m3)/(mol∙K) T temperature K P total pressure Pa C average molar concentration mol/m3 pA1 partial pressure of A in bulk Pa pA2 partial pressure of A in the interphase Pa pB0 partial pressure of B in bulk Pa pB2 partial pressure of B in the interphase Pa pBM log mean partial pressure of B Pa
- 6. Notations Symbol Explanation Units CA1molar concentration of A in bulk mol/m3 CA2 molar concentration of A in the interphase mol/m3 yA1 mole fraction of A in gaseuous mixture in bulk mol/mol yA2 mole fraction of A in gaseuous mixture in the interphase mol/mol xA1 mole fraction of A in a liquid solution in bulk mol/mol xA2 mole fraction of A in a liquid solution in the interphase mol/mol xBM log mean molar concentration of B in liquid solution mol/mol kC , k’C mass transfer coefficient in terms of concentrations in gases m/s kG , k’G mass transfer coefficient in terms of partial pressures in gases mol/(s∙m2∙Pa) kL , k’L mass transfer coefficient in terms of concentrations in liquids m/s ky , k’y mass transfer coefficient in terms of mole fractions in gases mol/(s∙m2) kx , k’x mass transfer coefficient in terms of mole fractions in liquids mol/(s∙m2)
- 7. Conversions • If theconcentration of A is expressed in the mole ratio unit: For the gas phase For the liquid phase Conversions between different types of mass transfer coefficients: 𝑁𝐴 = 𝑘𝑌 𝑌 𝐴1 − 𝑌 𝐴2 𝑁𝐴 = 𝑘𝑋 𝑋𝐴1 − 𝑋𝐴2 Equimolar counter diffusion Diffusion of A through non-diffusing B G A S L I Q U I D 𝑘𝐶 = 𝑘𝐺𝑅𝑇 = 𝑅𝑇 𝑃 𝑘𝑦 𝑘′𝐶 = 𝑘′𝐺𝑅𝑇 = 𝑅𝑇 𝑃 𝑘′𝑦 𝑘𝐿 = 𝑘𝑥 𝐶 𝑘′𝐿 = 𝑘′𝑥 𝐶 𝑘′𝑥 = 𝐶𝑘′𝐿 𝑘𝑥 = 𝐶𝑘𝐿 𝑘′𝐺 = 𝑘′𝑦 𝑃 = 𝑘′𝐶 𝑅𝑇 𝑘′𝑦 = 𝑃𝑘′𝐺 = 𝑃𝑘′𝐶 𝑅𝑇 𝑘𝐺 = 𝑘𝑦 𝑃 = 𝑘𝐶 𝑅𝑇 𝑘𝑦 = 𝑃𝑘𝐺 = 𝑃𝑘𝐶 𝑅𝑇
- 8. Approximations of masstransfer coefficients • There are approximations for mass transfer coefficients in a typical separation equipment: • Gas phase: kc ~ 10-2 m/s (film thickness l ~ 1 mm) • Liquid phase: kL ~ 10-5 m/s (film thickness l ~ 0.1 mm) • With these approximations it is easy to determine the orders of magnitude of other type of mass transfer coefficients. • For example, we can estimate the mass transfer coefficient in gaseous phase when A is diffusing through non-diffusing B in terms of mole fractions at 300 K and 3 bar at a low concentration: 𝑘𝑦 = 𝑃𝑘𝐶 𝑅𝑇 = 3 ∙ 105Pa ∙ 10−2m/s 8.31451 Pa ∙ m3 mol ∙ K ∙ 300K = 1.2 ∙ 10−10 mol m2 ∙ s
- 9. Dimensionless groups inmass transfer • Mass transfer coefficients and other important parameters (e.g. velocity, fluid properties, characteristic lengths) can also be expressed with so called dimensionless groups. • Dimensionless groups in mass transfer have many analogies to dimensional groups in heat transfer. • These are not covered more specifically in this course. Mass transfer Heat transfer Reynolds number Re The same Schmidt number Sc Prandtl number Pr Sherwood number Sh Nusselt number Nu Stanton number StM Stanton number StH Lewis number, Le = Sc/Pr Dimensionless numbers in mass transfer and heat transfer.
- 10. Mass transfer theories •There are several theories concerning the physical mechanism of convective mass transfer at a phase boundary. • These theories aim to determine the expressions for the mass transfer coefficients theoretically. • The most commonly used theories are: • Film theory (Film model) • Penetration theory • Surface renewal theory • Boundary layer theory • Film-penetration theory • These theories are not covered in this module.
- 11. Summary • When theturbulent flow has a significant role in mass transfer, it is called convective mass transfer. It is much more rapid than diffusion. • Convective mass transfer is a combination of diffusion and advection (the transport of a substance by bulk motion). • Mass transfer by convection involves the transport of material between a boundary surface and a moving fluid. • Mass transfer coefficients are used to simplify the calculations. • They are determined separetarly for gas and liquid phases. • They can be expressed in terms of concentrations, mole fractions or partial pressures (for gases). • There are several theories which aim to determine the mass transfer coefficients theoretically.
- 12. This project hasreceived funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869993. References Benitez, J. 2016. Principles and Modern Applications of Mass Transfer Operations. Wiley, pp. 91-96. Dutta, B. K. 2007. Principles of mass transfer and separation processes. New Delhi: Prentice-Hall, pp. 74-117. Treybal, R. E. 1980. Mass-transfer operations. 3rd ed. Auckland: McGraw-Hill, pp. 45-71. Videos: • Mass transfer coefficients: https://youtu.be/cYNqJU65oNo • Mass transfer coefficients in equimolar counter diffusion: https://youtu.be/cPUCKrdWGtE