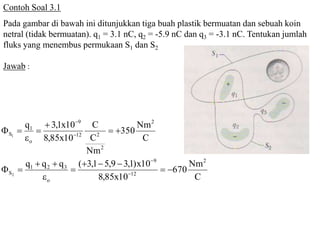
Bab 3 membahas hukum Gauss tentang fluks medan listrik yang melewati permukaan tertutup. Hukum Gauss menyatakan bahwa jumlah fluks medan listrik yang melewati permukaan tertutup sebanding dengan jumlah muatan di dalam permukaan tersebut. Bab ini juga menjelaskan konsep fluks dan hubungan antara hukum Gauss dengan hukum Coulomb, serta penerapan hukum Gauss pada berbagai simetri permukaan tertutup.

1. BAB 3 HUKUM GAUSS
 PENGERTIAN FLUKS
 FLUKS MEDAN LISTRIK
 HUKUM GAUSS
 HUBUNGAN HUKUM GAUSS DAN HUKUM COULOMB
 SIMETRI SILINDER
 SIMETRI BIDANG DATAR
 SIMETRI BOLA

2.  PENGERTIAN FLUKS
• Misalkan terdapat aliran udara yang mengalir
melalui suatu lup tertutup seluas A dengan
kecepatan v
• Didefinisikan vektor luas A sebagai vektor
yang normal/tegak lurus pada permukaan lup
• Bila vektor kecepatan v searah dengan vektor
A, maka debit aliran udaranya adalah  = vA
dengan satuan [(m/s) (m 2) = m3 /s], debit
volume ini disebut fluks
• Flux berasal dari bahasa Latin yang berarti
mengalir
• Bila vektor kecepatan v membentuk sudut 
dengan vektor luas A, maka debitnya adalah
 = vAcos 
• Bila dinyatakan dengan notasi vektor
 = v ● A
• Pengertian fluks kemudian dapat diperluas
untuk besaran lain yang tidak ada
hubungannya dengan kecepatan

3.  FLUKS MEDAN LISTRIK
• Misalkan suatu permukaan tertutup A
berada di dalam medan listrik E
• Permukaan tertutup ini dibagi-bagi
menjadi ΔA yang kecil sekali sehingga
dapat dianggap bidang datar, sehingga
fluksnya adalah ΔA●E
• Jumlah total fluks yang menembus
permukaan tertutup menjadi :
• Fluks yang keluar dapat dianggap
positip sedangkan fluks yang masuk
dianggap negatip
   dAEAdE


4.  HUKUM GAUSS
• Hukum Gauss menyatakan
bahwa jumlah fluks medan
listrik yang menembus suatu
permukaan tertutup sebanding
dengan jumlah muatan yang
ada di dalam permukaan
tertutup tersebut
qAdEq oo  

• Permukaan tertutup tersebut sering disebut sebagai permukaan Gauss
• Jumlah fluks yang menembus permukaan S1 positip (ada muatan positip)
• Jumlah fluks yang menembus permukaan S2 negaitip (ada muatan negatip)
• Jumlah fluks yang menembus permukaan S3 nol (tidak ada muatan)
• Jumlah fluks yang menembus permukaan S4 nol (jumlah muatan nol)

5. Contoh Soal 3.1
Pada gambar di bawah ini ditunjukkan tiga buah plastik bermuatan dan sebuah koin
netral (tidak bermuatan). q1 = 3.1 nC, q2 = -5.9 nC dan q3 = -3.1 nC. Tentukan jumlah
fluks yang menembus permukaan S1 dan S2
Jawab :
C
Nm
670
10x85,8
10x)1,39,51,3(qqq
C
Nm
350
Nm
C
C
10x85,8
10x1,3q
2
12
9
o
321
S
2
2
212
9
o
1
S
2
1
















6.  HUBUNGAN HUKUM GAUSS DAN HUKUM COULOMB
•Misalkan terdapat sebuah muatan
titik q dan sebuah permukaan
tertutup berupa bola berjari-jari r
• Dari hukum Gauss diperoleh :
•Karena simetris, E konstan
diseluruh permukaan sehingga :
• Dengan demikian :
•Hukum Gauss adalah cara lain
untuk menyatakan hukum Coulomb
qAdEo  

q)r4(E
qEAdAE
2
o
oo

 
2
o r
q
4
1
E



7.  SIMETRI SILINDER
• Misalkan terdapat muatan garis tak hingga
dengan rapat muatan 
• Dipilih permukaan Gauss berupa silinder
setinggi h dan berjari-jari r dengan sumbu
yang terletak pada muatan garis
• Medan listrik seragam menembus selimut
silinder dan tidak ada fluks yang menembus
tutup atas dan tutup bawah silinder
• Dari hukum Gauss diperoleh :
r2
1
E
h
q
)r2(E
qh)r2(E
qEAdAEAdE
o
i
o
io
i
o
utlimse
oo





  


8.  SIMETRI BIDANG DATAR
• Misalkan terdapat muatan bidang tak hingga (non konduktor) dengan rapat muatan 
• Dipilih permukaan Gauss berupa silinder dengan luas tutup kiri dan kanan sebesar A
• Medan listrik seragam di kiri dan kanan bidang yang arahnya keluar
• Tidak ada fluks yang menembus selimut silinder
• Dari hukum Gauss diperoleh :
o
i
o
ioo
kanan
io
kiri
o
io
2
E
A
q
E2
qEAEA
qAdEAdE
qAdE












9.  SIMETRI BOLA
• Misalkan terdapat sebuah kulit bola bermuatan q yang terdistribusi seragam diseluruh
permukaannya
• Dipilih dua permukaan Gauss berupa bola S1 yang berjari-jari < R dan bola S2 yang
berjari-jari  R
• Dari hukum Gauss diperoleh :
Rr
r
q
4
1
E
q)r4(E
qqAdE
Rr0E
0qAdE
2
o
2
o
S,i
S
o
S,i
S
o
2
2
1
1












10. Contoh Soal 3.2
Sebuah muatan titik sebesar 1,8 µC terletak di tengah-tengah
sebuah kubus berjari-jari 55 cm. Hitung fluks listrik yang
menembus permukaan kubus tersebut
Jawab :
C
Nm
10x034.2
10x85.8
10x8.1q
qdA.EdA.E
2
5
12
6
o
o








11. Contoh Soal 3.3
Sebuah muatan titik q terletak pada jarak d/2 dari pusat sebuah bujur
sangkar bersisi d seperti terlihat pada gambar di bawah ini. Hitung fluks
listrik yang menembus bujur sangkar tersebut
Jawab :
o
sangkarbujur
sangkarbujur
sangkarbujuroo
kubus
kubusoo
o
6
q
EA
6
q
EAdA.E
qEAdA.E
qdA.EdA.E









12. Contoh Soal 3.4
Medan listrik di sekitar permukaan bumi mempunyai arah vertikal ke
bawah. Pada ketinggian 200 m medan listrik terukur sebesar 100 N/C
sedangkan pada ketinggian 300 m medan listrik terukur sebesar 60 N/C.
Berapa jumlah muatan yang terdapat di dalam kubus bersisi 100 m
dengan permukaan horisontalnya terletak pada ketinggian 200 m dan
300 m.
Jawab :
C54.3)100)(10060)(10x85.8(
AEAEq
qdAEdAEdAE
A)EE(qqdA.E
212
bawahbawahoatasataso
bawah
o
atas
o
kubus
o
21oo








13. Contoh Soal 3.5
Sebuah bola isolator bermuatan q dan berjari-jari R mempunyai rapat
muatan volume seragam. Dengan menggunakan hukum Gauss tentukan
medan listrik di dalam dan diluar bola.
Jawab :
3
o
3
3
2
o
3
3
S
o
S
ro
3
3
3
3
rr
3
R
qr
4
1
E
R
qr
)r4(E
R
qr
dAEqdAE
R
qr
r
3
4
R
3
4
q
Vq
R
3
4
q
).a
11









r
R
r
).b
2
o
2
o
S
o
S
o
r
q
4
1
Eq)r4(E
qdAEqdAE).b
11


 
Seperti muatan titik
S1
S2

14. Contoh Soal 3.6
Bola konduktor pejal berongga
mempunyai jari-jari dalam R1 dan jari-
jari luar R2 di beri muatan sebesar -2q.
Dipusat bola berongga ini terdapat
muatan titik sebesar +q. Tentukan
medan listrik dimana-mana dengan
menggunakan hukum Gauss.
Jawab :
2
o
2
o
S
o1
r
q
4
1
Eq)r4(EqdAERr
1

 
r
R2
R1
r
q)q(q2''qq'q0'qqq0dAE
0ERrR
2S
io
21



Di dalam konduktor
-q
-q
2
o
2
o
S
io2
r
q
4
1
Eqq2q)r4(EqdAERr
3

 
S3
S2
S1

15. Soal Latihan 3.1
Sebuah konduktor yang berbentuk silinder sepanjang L dan
bermuatan sebesar +q dikelilingi oleh konduktor lain berbentuk
silinder berongga juga sepanjang L yang bermuatan – 2q seperti
terlihat pada gambar di bawah ini. Dengan menggunakan hukum
Gauss tentukan :
a). Medan listrik diluar silinder berongga
b). Distribusi muatan pada silinder berongga
c). Medan listrik diantara kedua konduktor
rL2
q
E).a
o


rL2
q
E).c
o


-q pada dinding dalam
-q pada dinding luar

16. Soal Latihan 3.2
Sebuah bola isolator pejal dengan jari-jari R1 dikelilingi oleh oleh
bola berongga konduktor netral berjari-jari dalam R2 dan berjari-
jari luar R3. Bola isolator mempunyai rapat muatan volume
sebesar (r)=br dimana b adalah konstan dan r adalah jarak dari
pusat bola. Hitung medan listrik di :
a). r <R1
b). R1< r < R2
c). R2< r < R3
d). R>R3
Hitung juga rapat muatan induksi di dinding dalam bola berongga
2
2
4
1
2
4
1
o
2
4
1
o
2
o
R4
bR
'
r
bR
4
1
E).d0E).c
r
bR
4
1
E).bbr
4
1
E).a








17. Soal Latihan 3.3
Sebuah bola berongga non konduktor mempunyai jari-jari dalam a
dan jari-jari luar b serta mempunyai rapat muatan volume =A/r,
dimana A suatu konstanta dan r adalah jarak dari pusat bola
berongga. Berapa harga A agar medan listrik di dalam bola
berongga akan uniform.
2
a2
q
A

