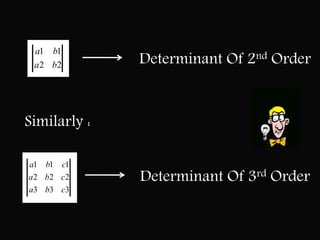
This document discusses determinants of matrices. It begins by defining determinants of 2nd and 3rd order matrices, then defines the determinant of an nth order matrix as an n×n array with numbers arranged in n rows and columns. It explains that the leading diagonal runs from the top left to bottom right. The document then provides more details on calculating 2nd and 3rd order determinants using cofactors. It introduces Laplace's expansion method for calculating determinants by expanding along rows or columns. Finally, it lists some properties of determinants.

2. What Really It Is ?

3. Determinant Of 2nd Order
Similarly :
Determinant Of 3rd Order
333
222
111
cba
cba
cba
22
11
ba
ba

4. In General :
Determinant Of nth Order
A block of n2 arranged in form of
n-rows and n-columns
Diagnol through left-hand top corner is
called Leading or Principal Diagnol
ln...
.
.
.
...
...
...
.
.
.
.
.
.
.
.
.
.
.
.
4...4444
3...3333
2...2222
1...1111
dncnbnan
ldcba
ldcba
ldcba
ldcba

5. • For 2nd Order determinant:
•
• For 3rd Order determinant:
• Co-factor is obtained by deleting the row &
column which intersect in that element with
proper sign.
• The sign of an element in the ith row and jth
column is (-1)i+j :The Co-factor of b3 i,e., B3 =
(-1)3+2 22
11
ca
ca
a1b2 – a2b122
11
ba
ba
333
222
111
cba
cba
cba
Co-Factors

6. Laplace’s Expansion
• A determinant can be expanded in terms of
any row( or column) as follows:












333
222
111
cba
cba
cba
Expanding by R1 (
i.e., 1st Row):
= a1A1 +b1B1 +c1C1
= a1
33
22
cb
cb
-b1 33
22
ca
ca
+
c1 33
22
ba
ba
Expanding by C2 ( i.e., 2nd
Column):
= -b1B1 +b2B2 –b3B3= -b1
33
22
ca
ca
+b2 33
11
ca
ca
-b3
22
11
ca
ca
1
2

7. Solution To is:
a1( b2c3 - b3c2) –b1( a2c3 – a3c2) + c1( a2b3 – a3b2)
1
Solution To is:
–b1( a2c3 – a3c2) +b2( a1c3 – a3c1) –b3( a1c2 – a2c1)
2

8. For Example: Find The Determinant Of
=
987
654
321
Expanding by R1 (
i.e., 1st Row):
= a1A1 +b1B1 +c1C1
= 1 98
65 -2
97
64 +3
87
54
= 1((5*9) – (6*8)) –2((4*9) – (6*7)) +3((4*8) – (5*7))
= 1(45 – 48) -2(36 – 42) +3(32 – 35)
= -3 +12 -3
=6

9. Properties Of Determinant :
1. A determinant remains unaltered by changing
its rows into columns and columns into rows.
2. If two parallel lines of a determinant are
interchanged, the determinant retains its
numerical value but changes in sign.
3. A determinant vanishes if two parallel lines are
identical.
4. If each element of a line be multiplied by same
factor, the whole detreminant is multiplied by
that factor.
5. If each element of a line consists of m terms,

10. Thank You