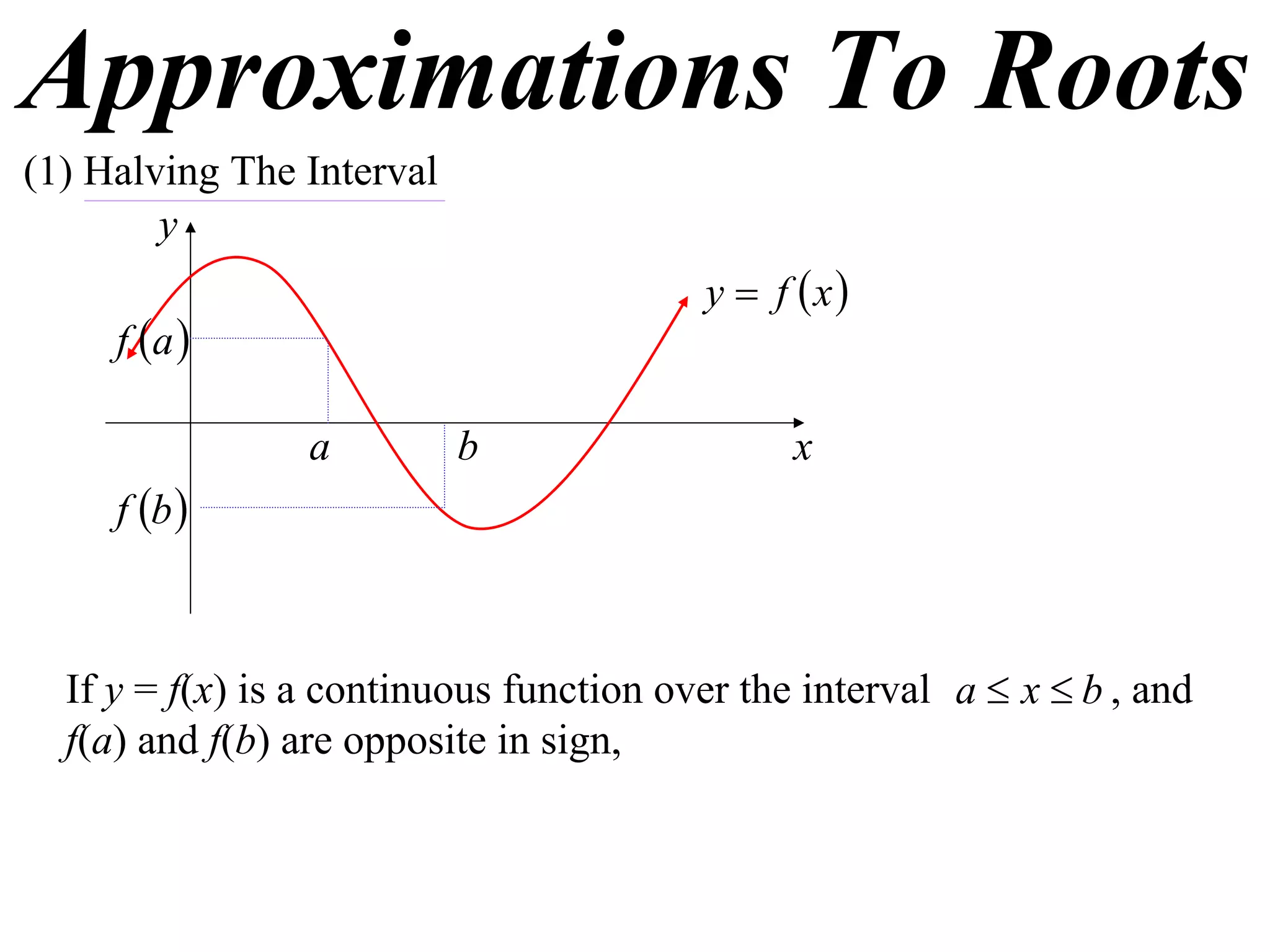
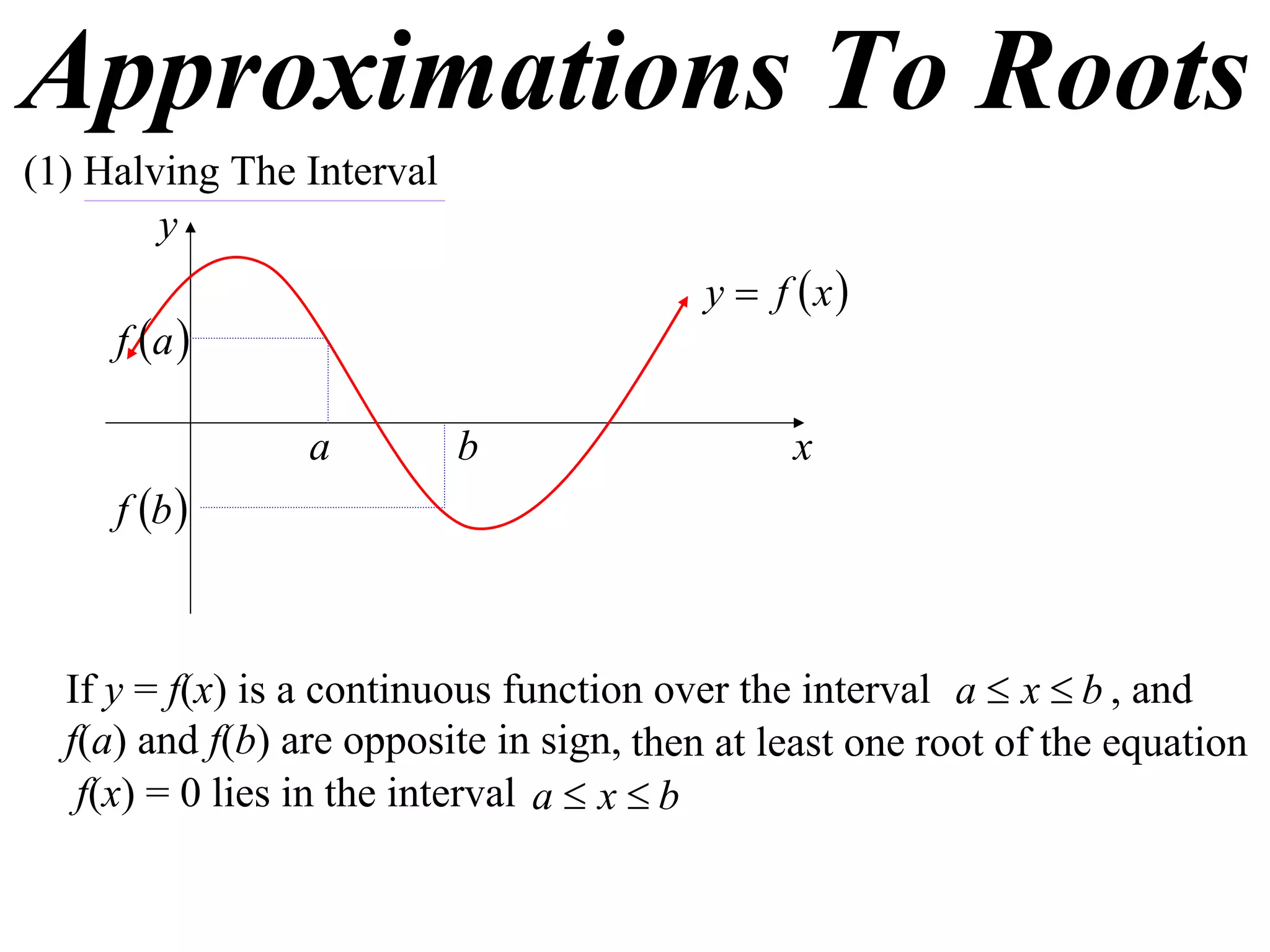
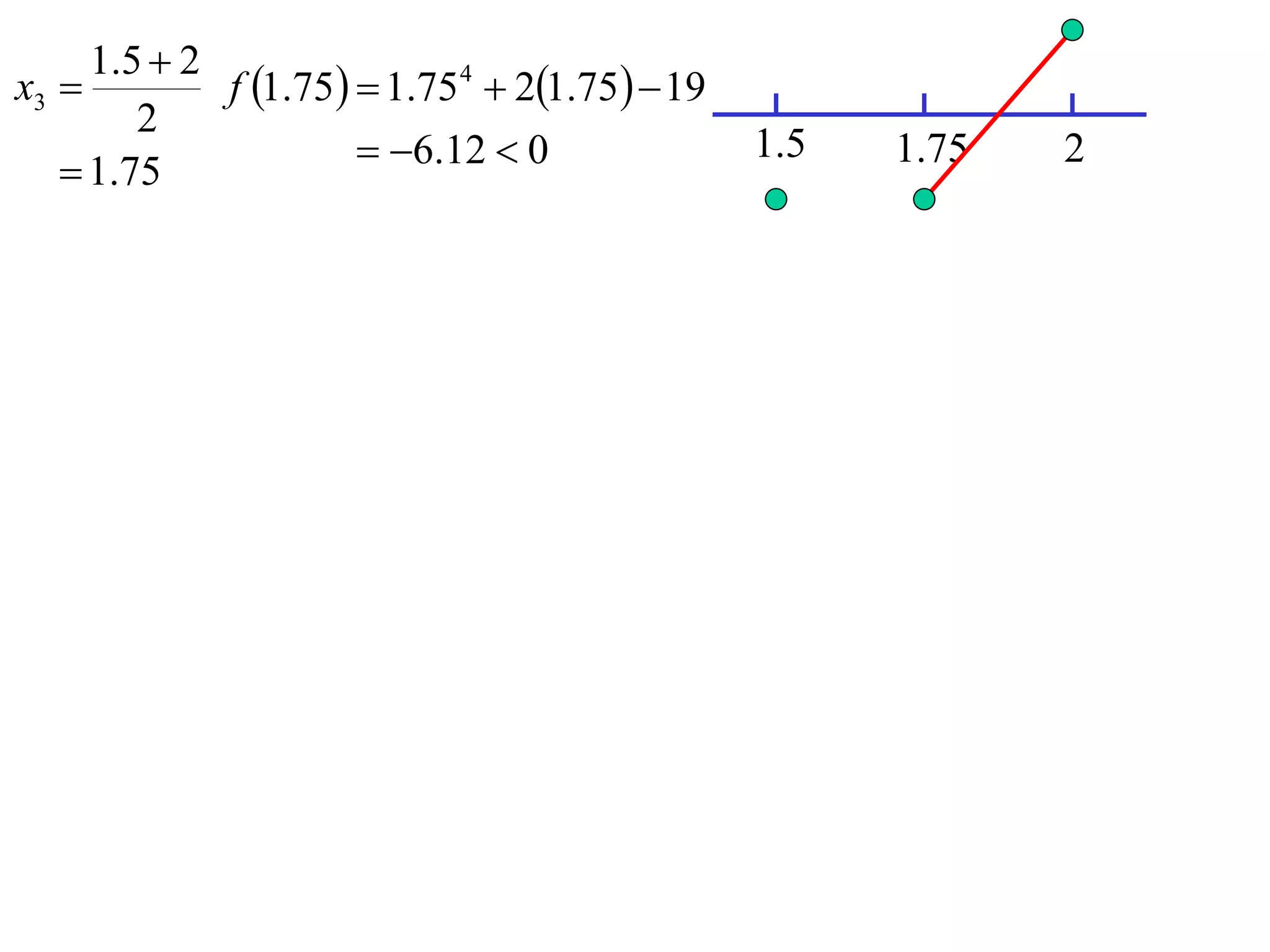
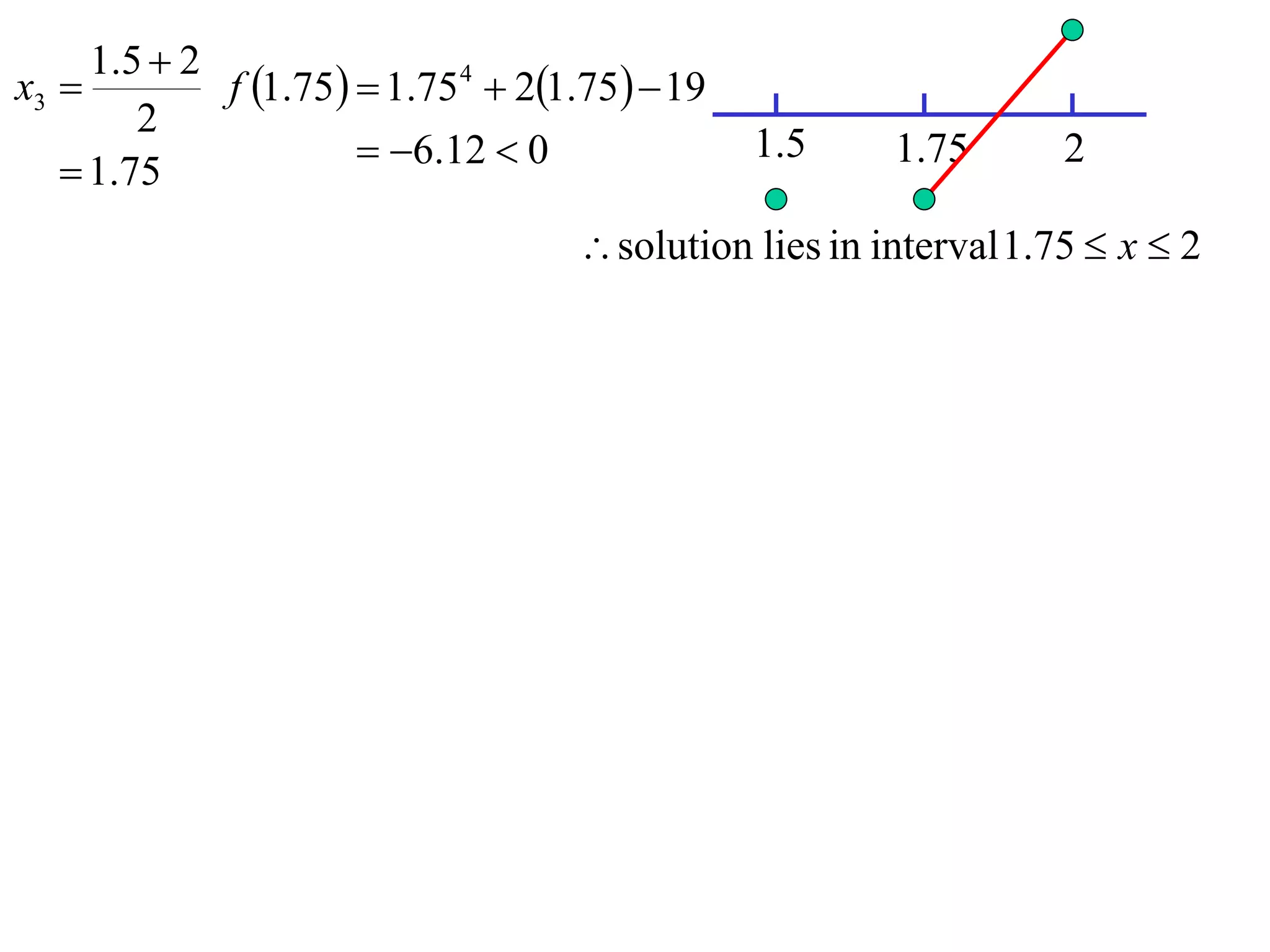
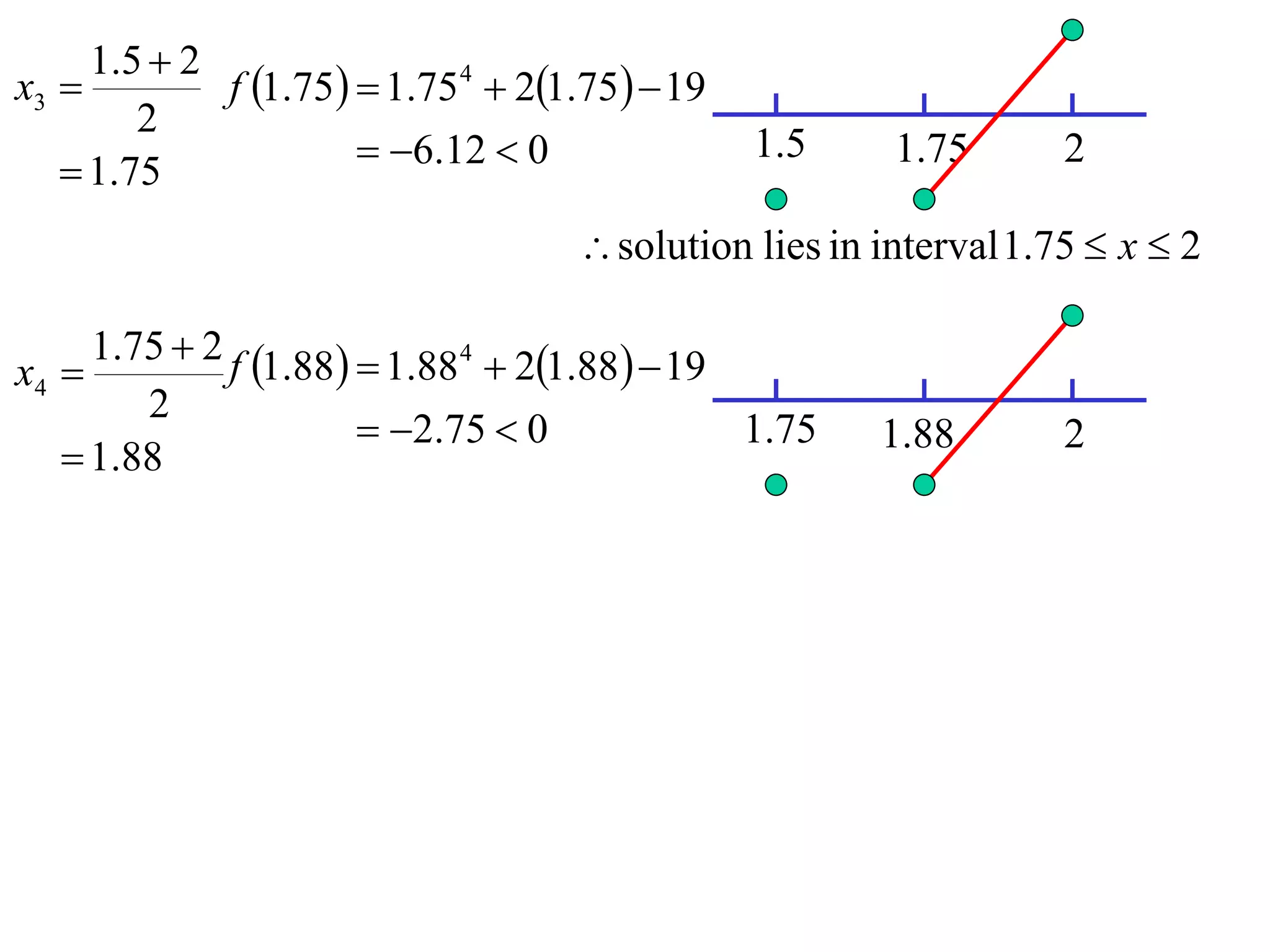
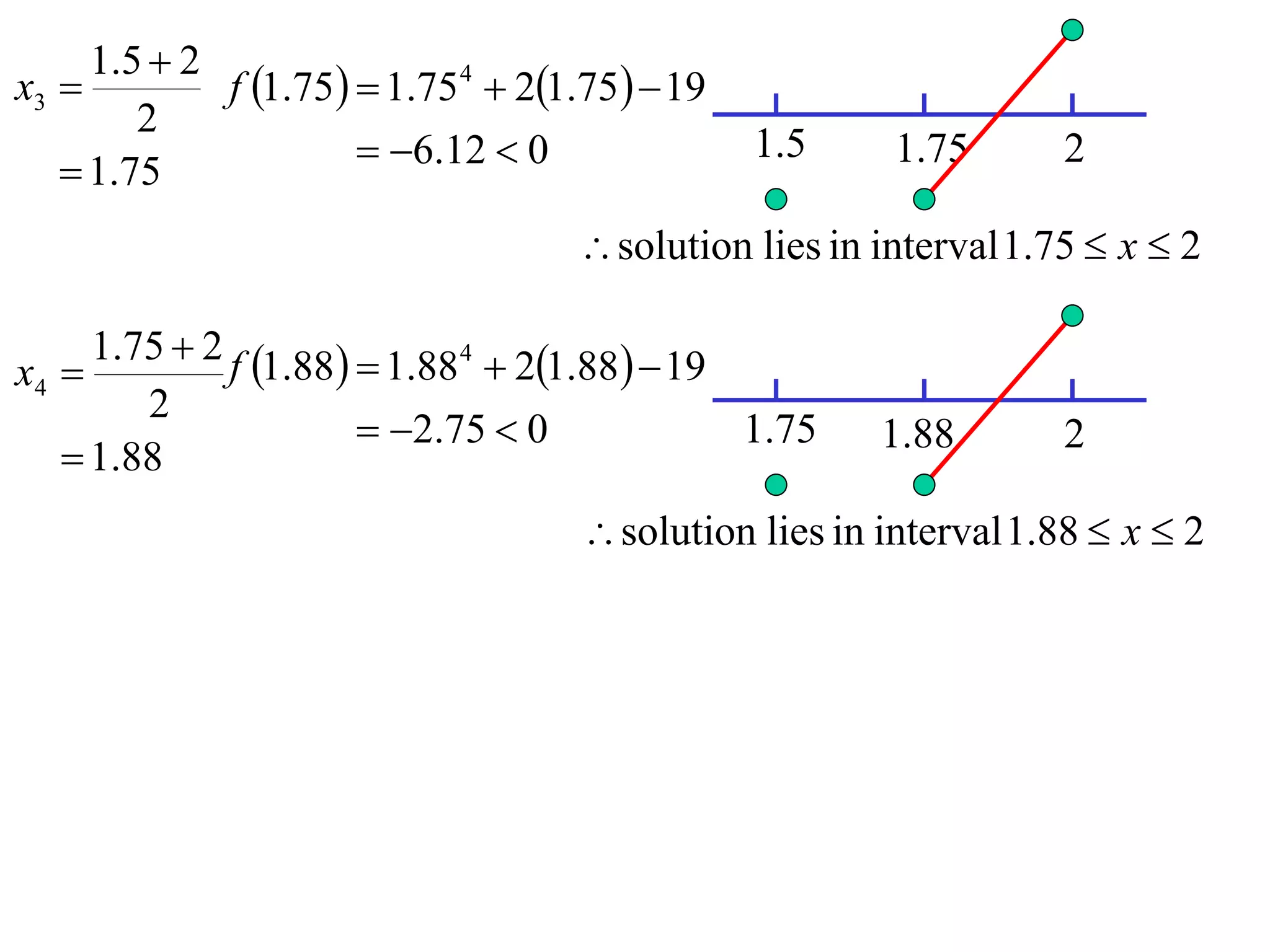
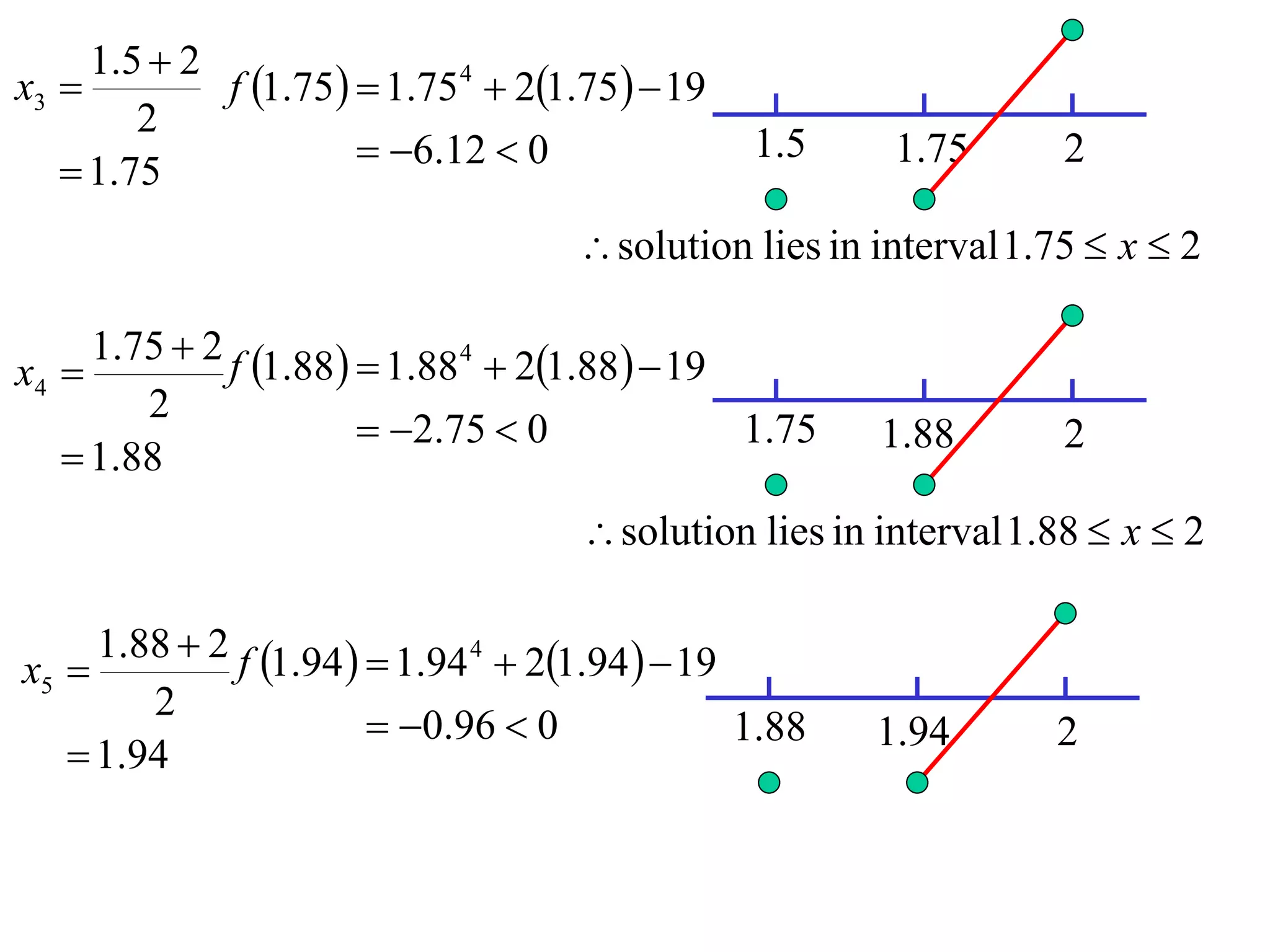
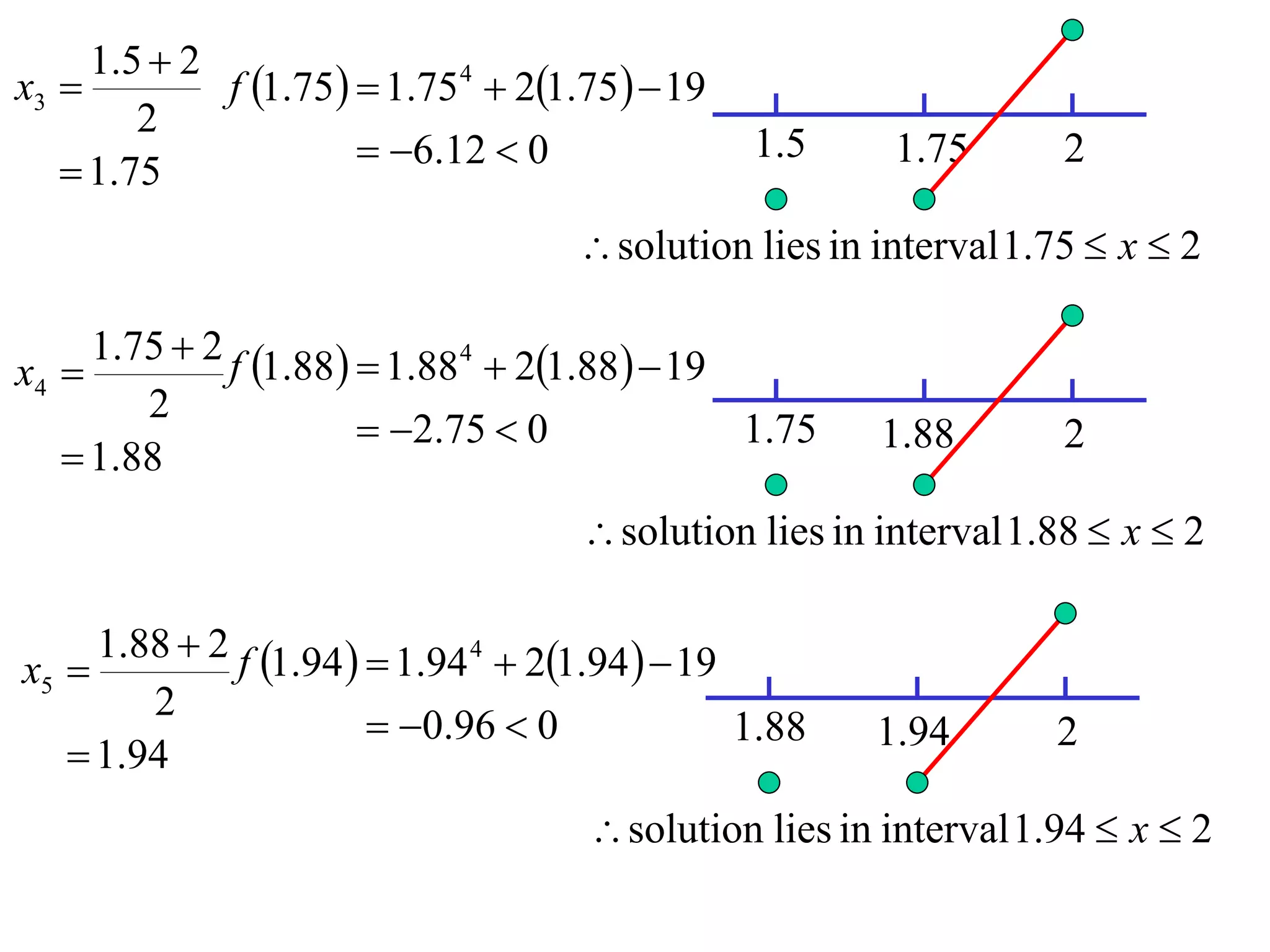
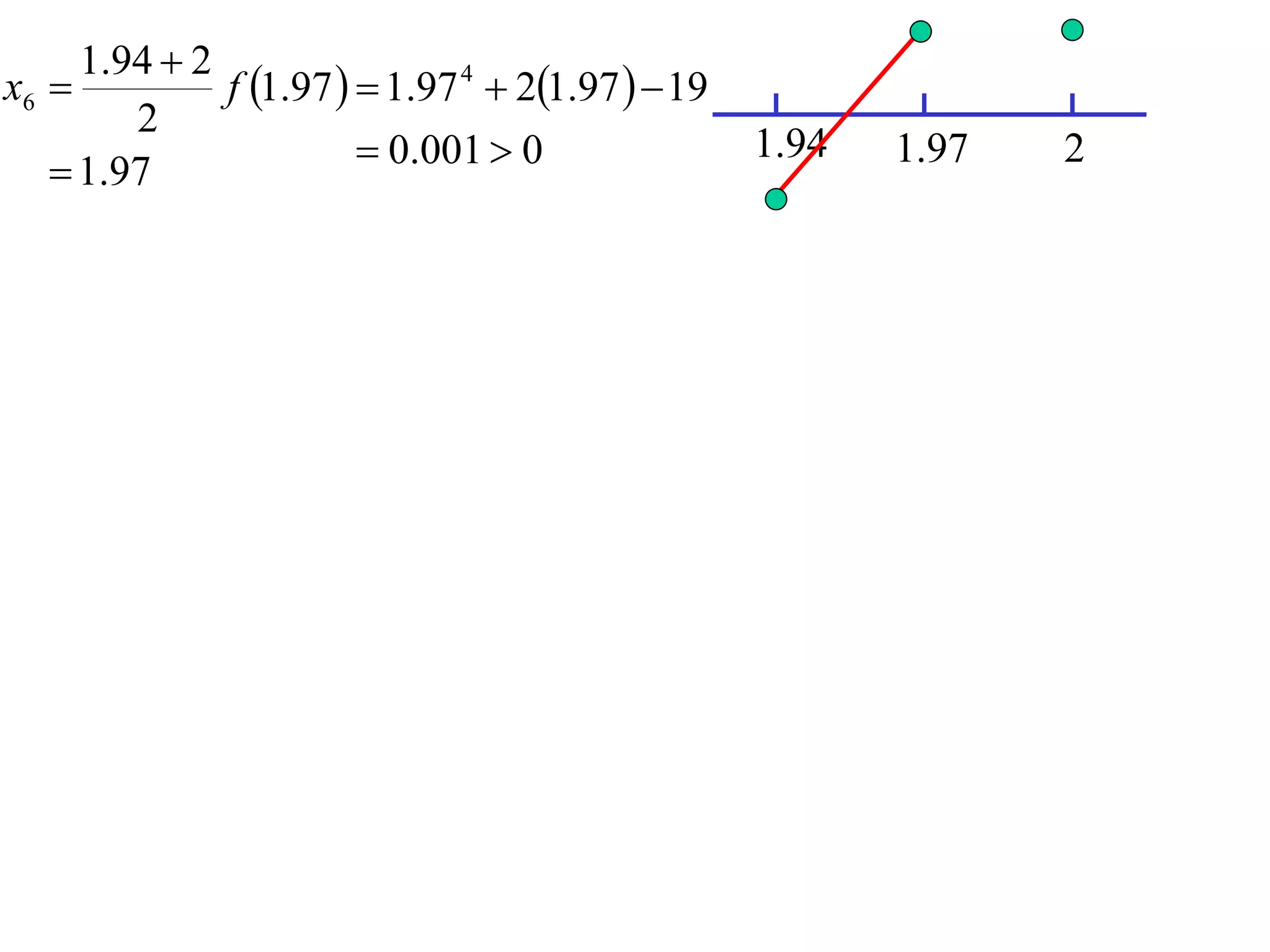
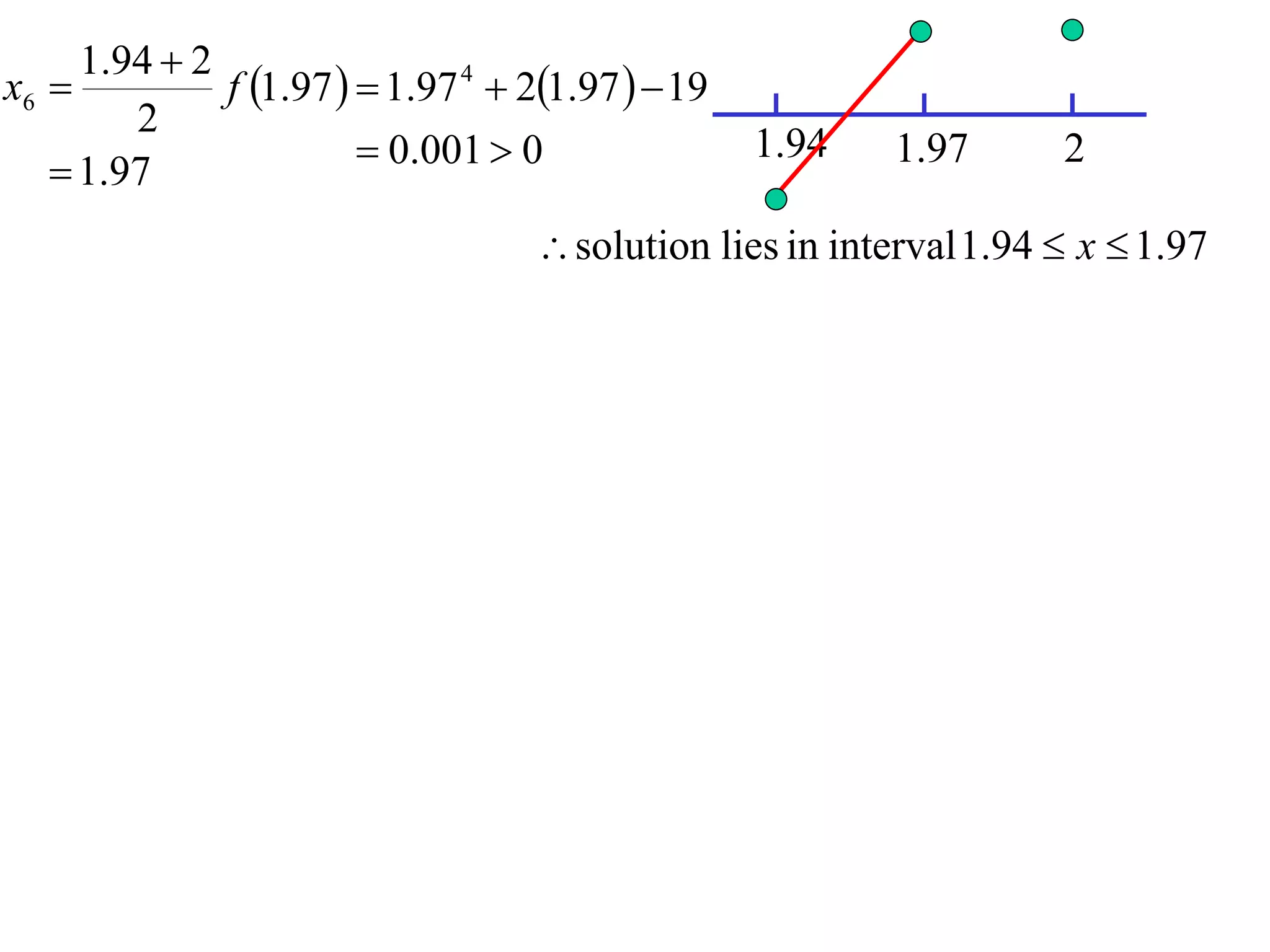
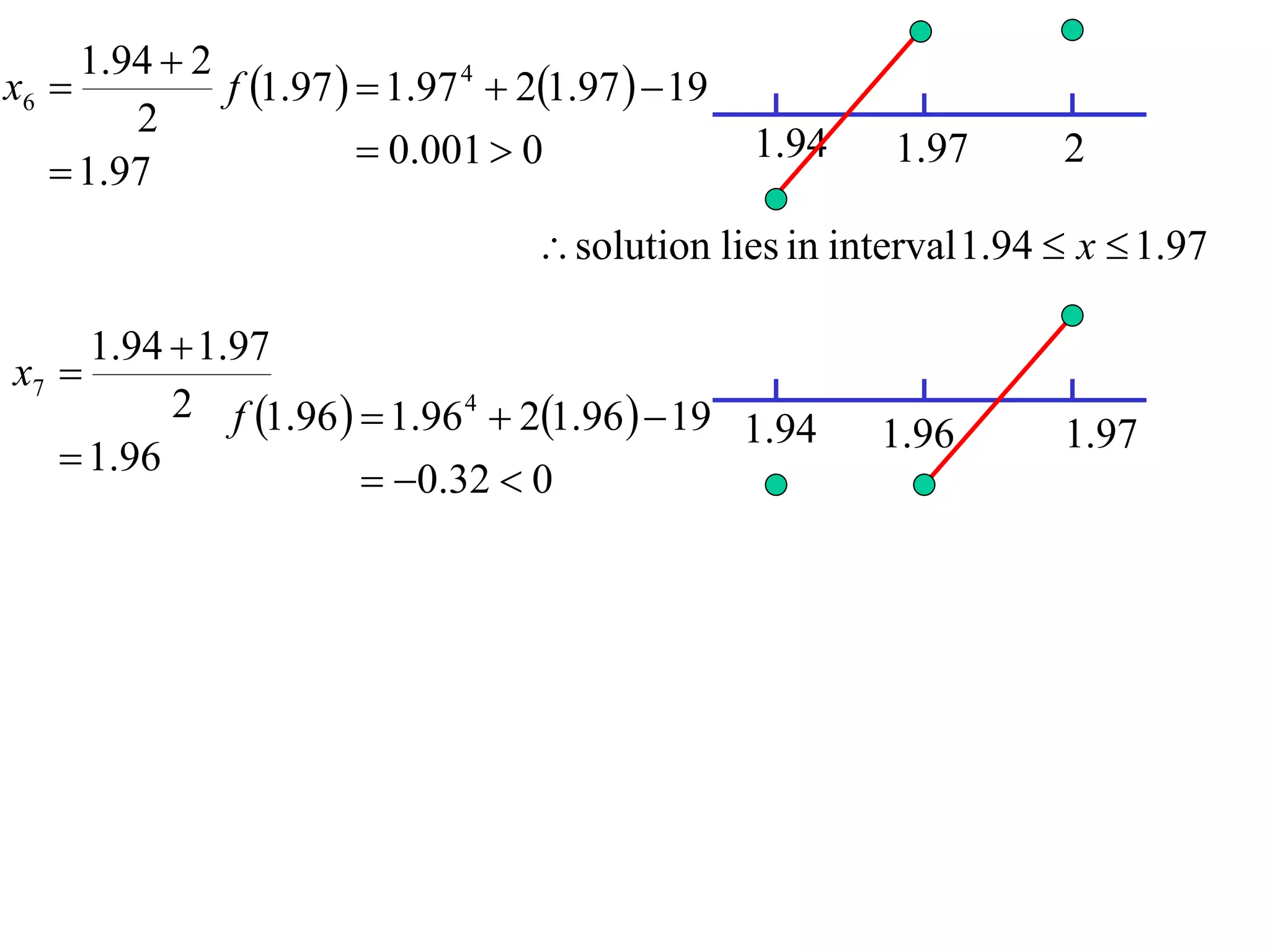
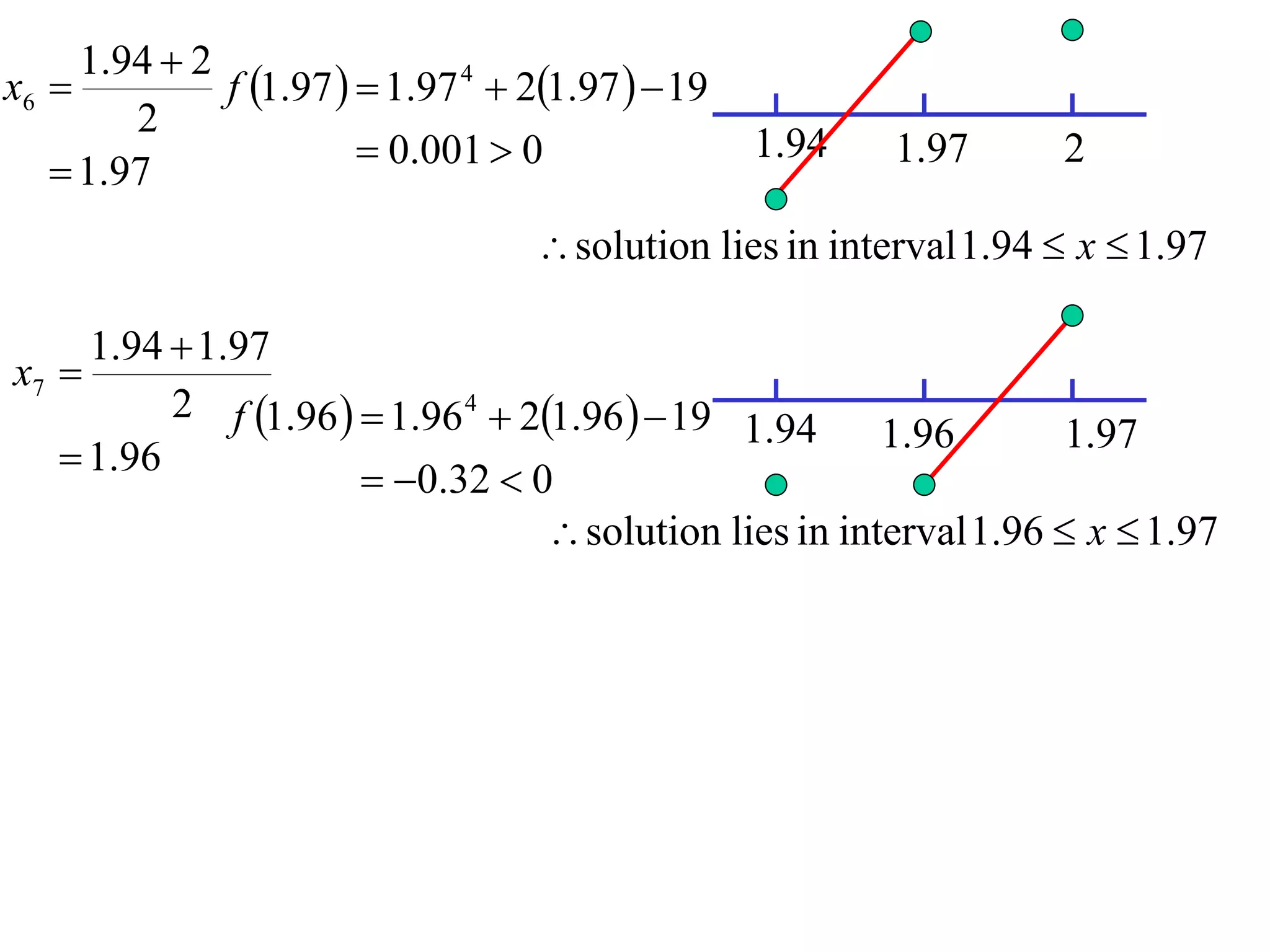
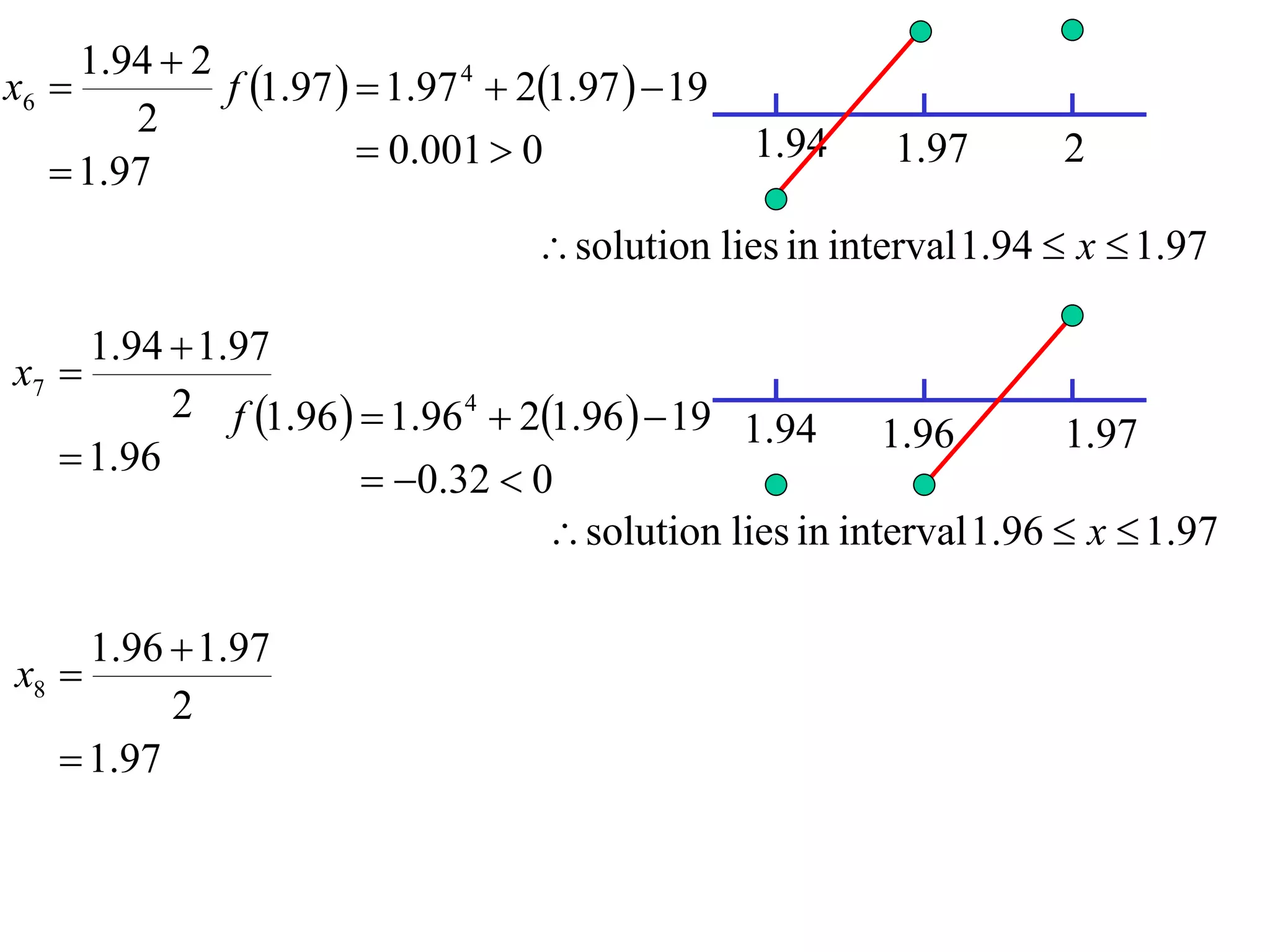
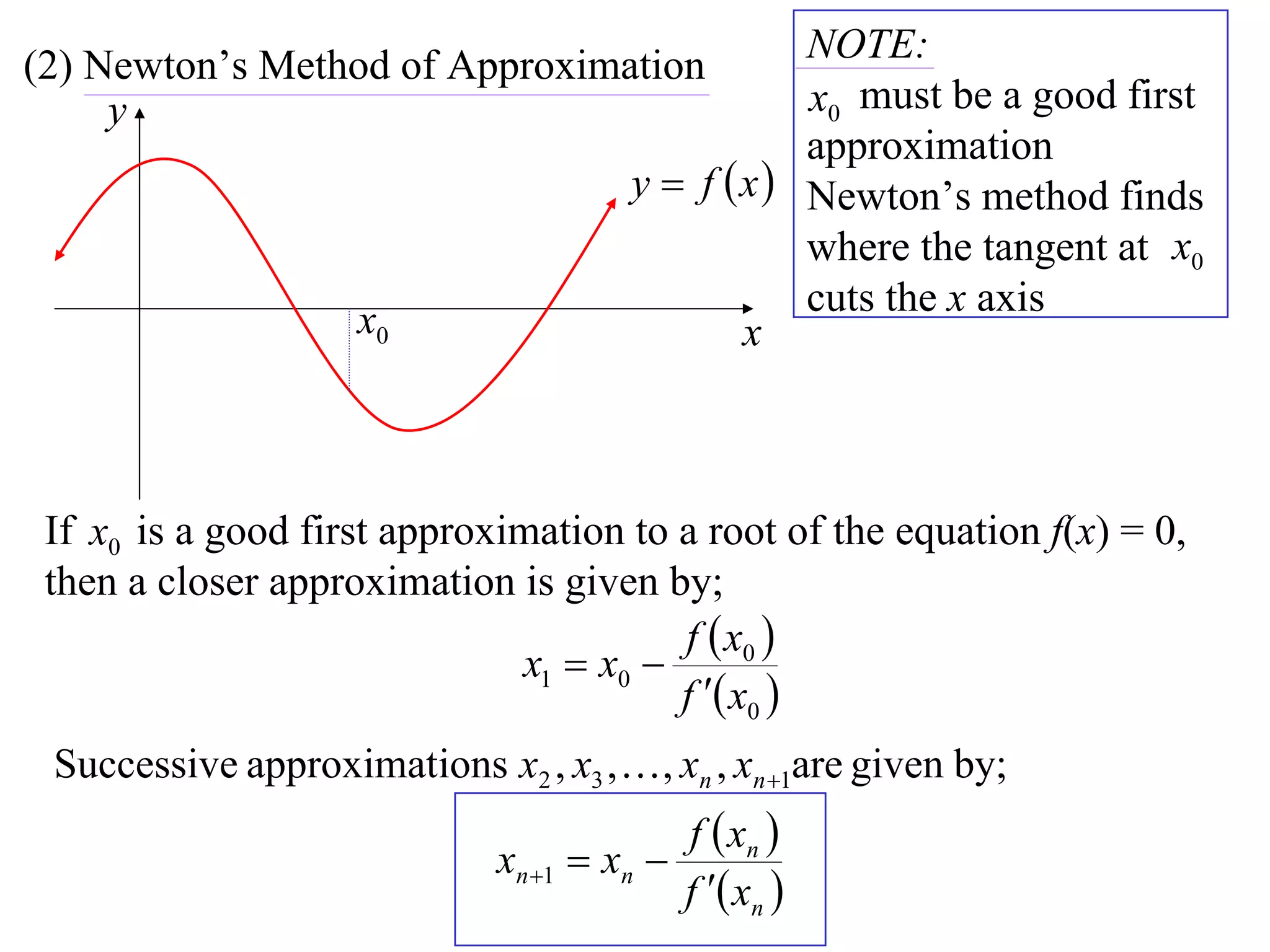
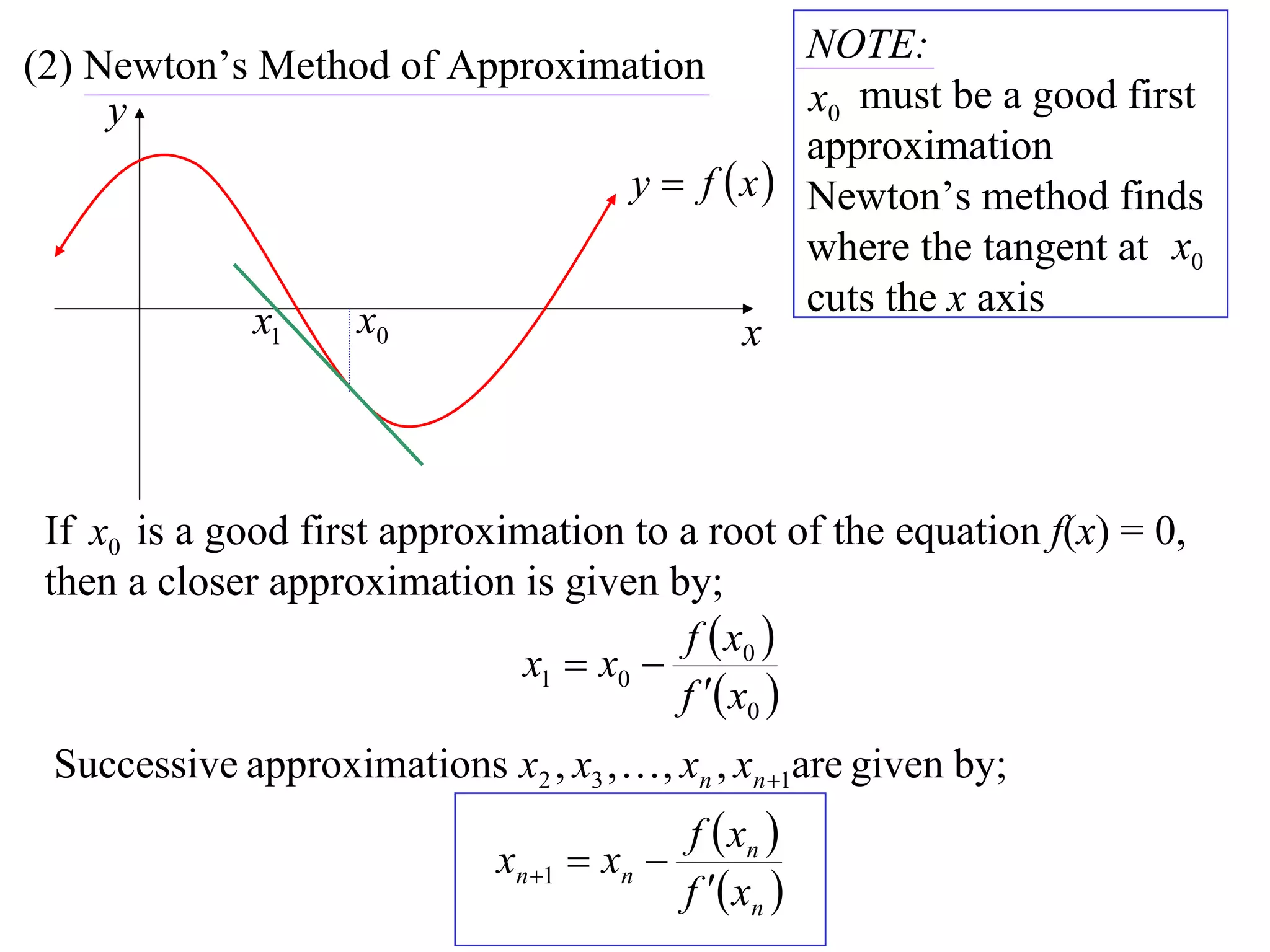
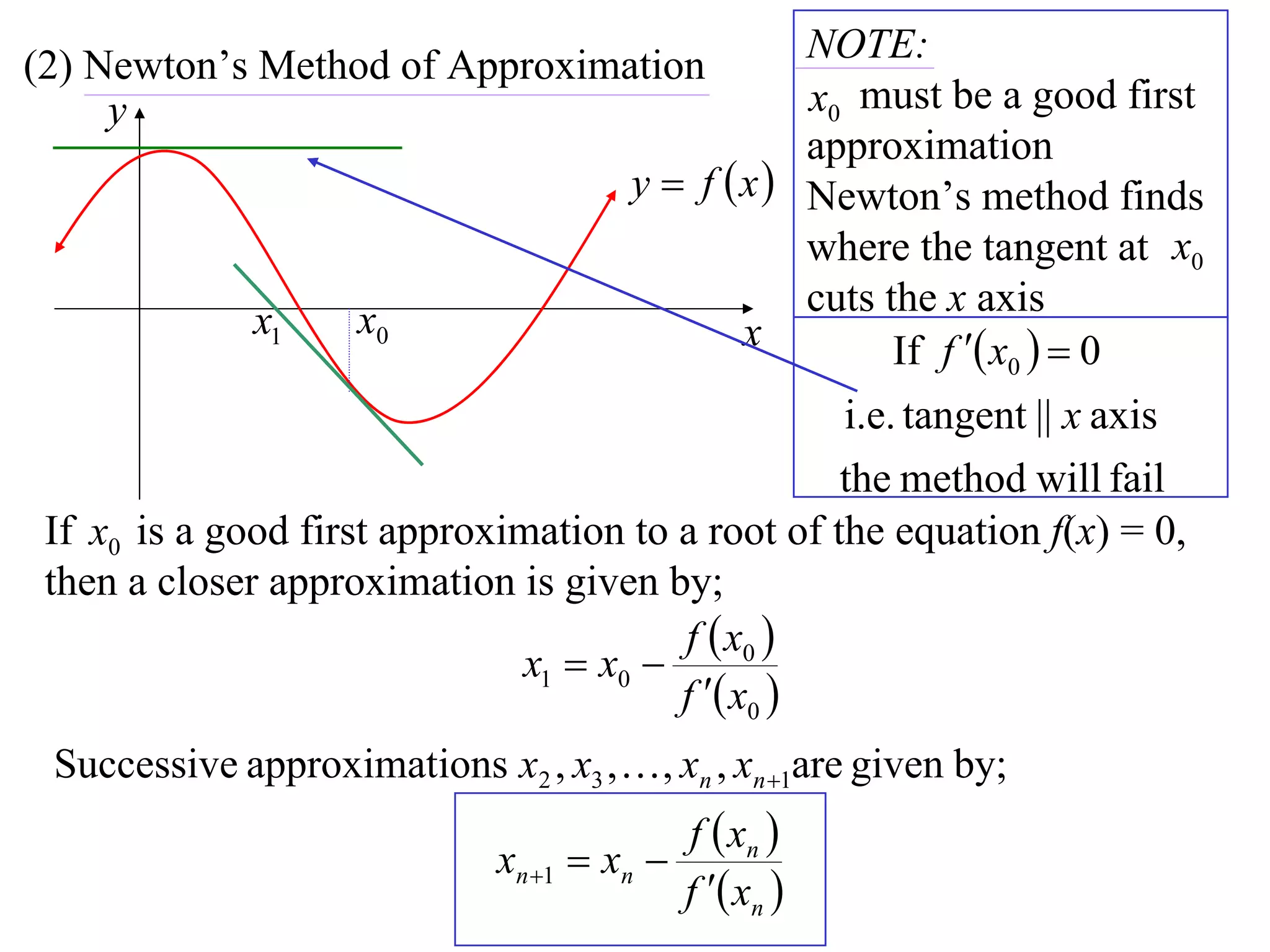
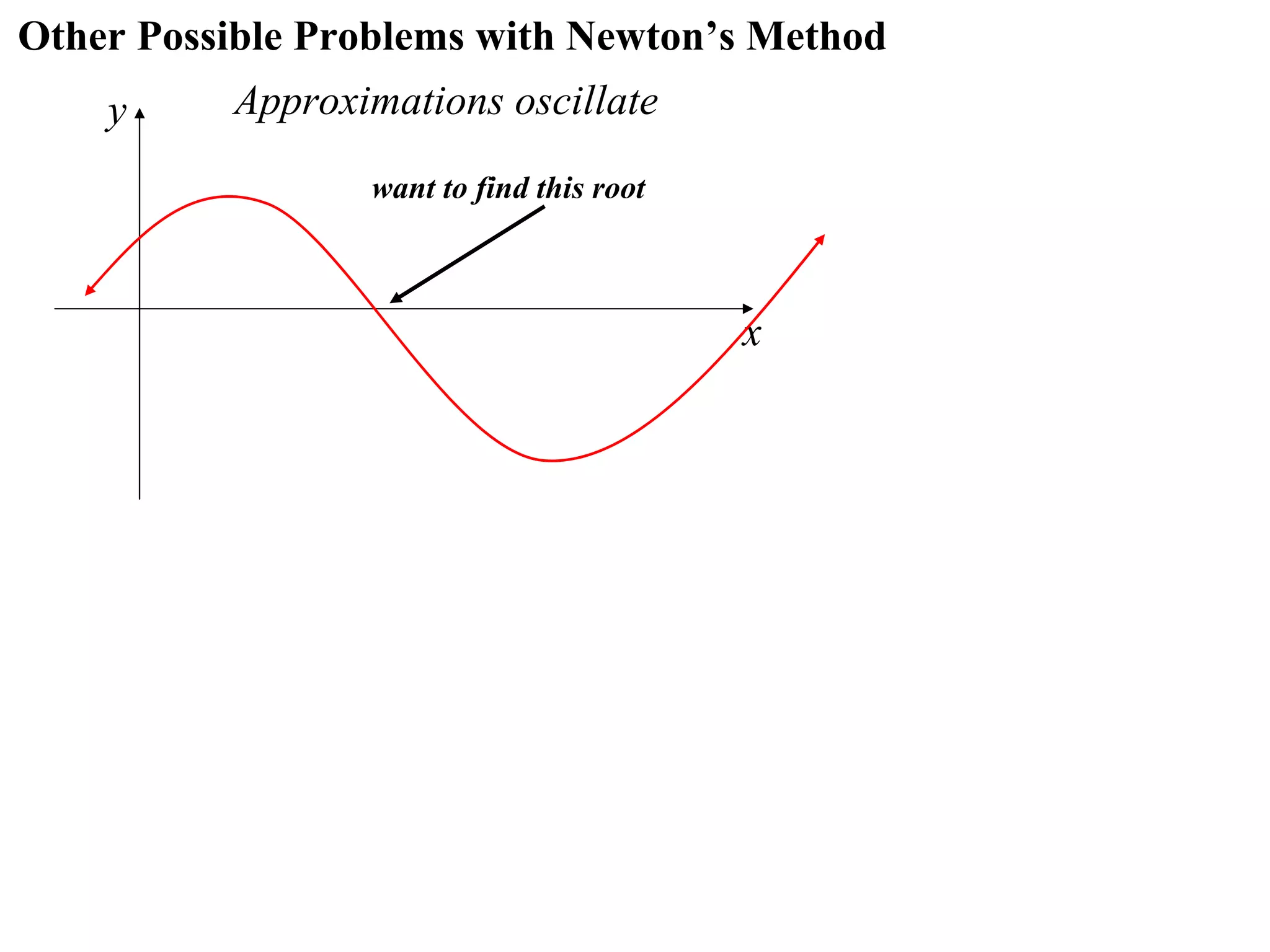
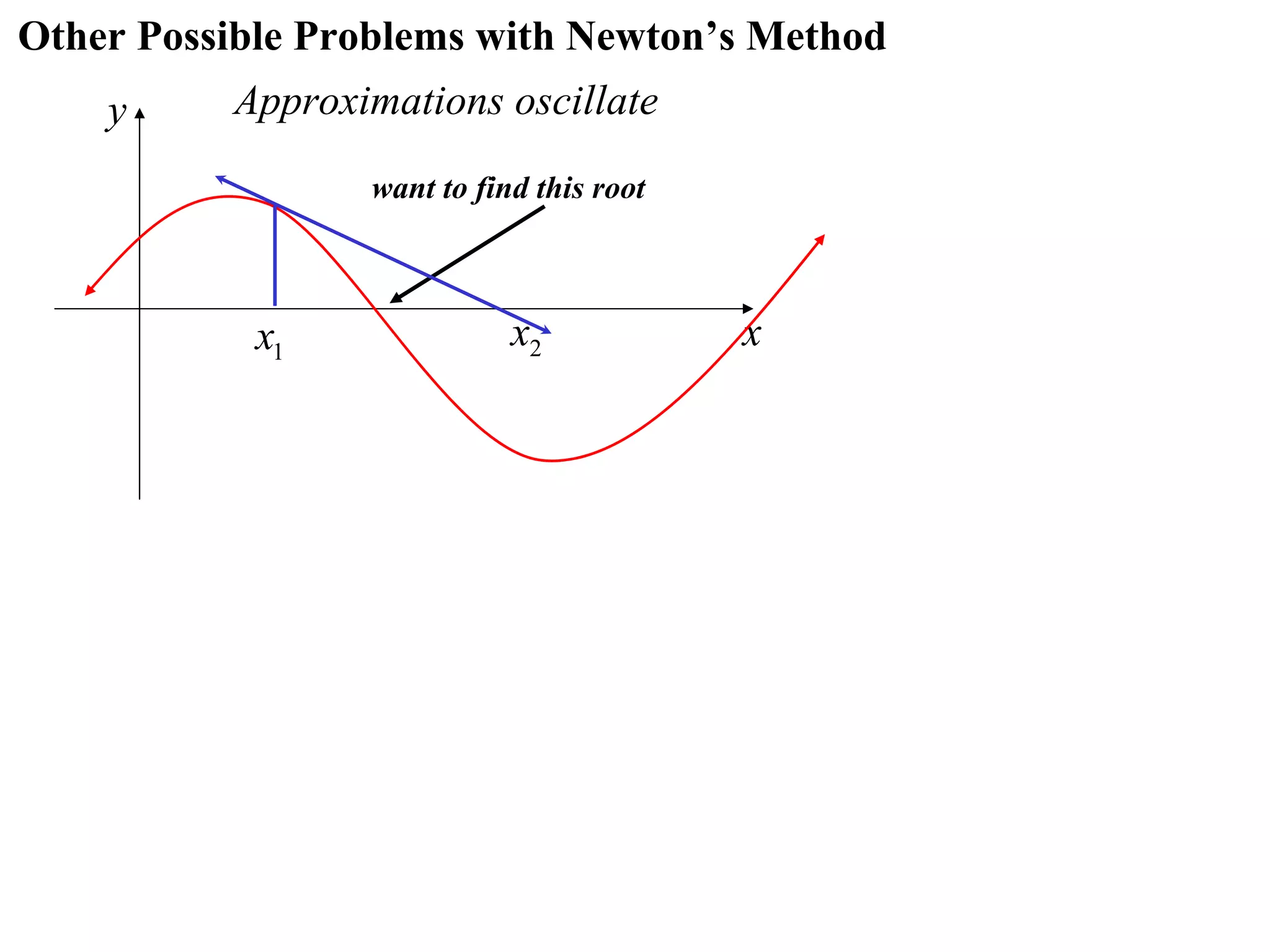
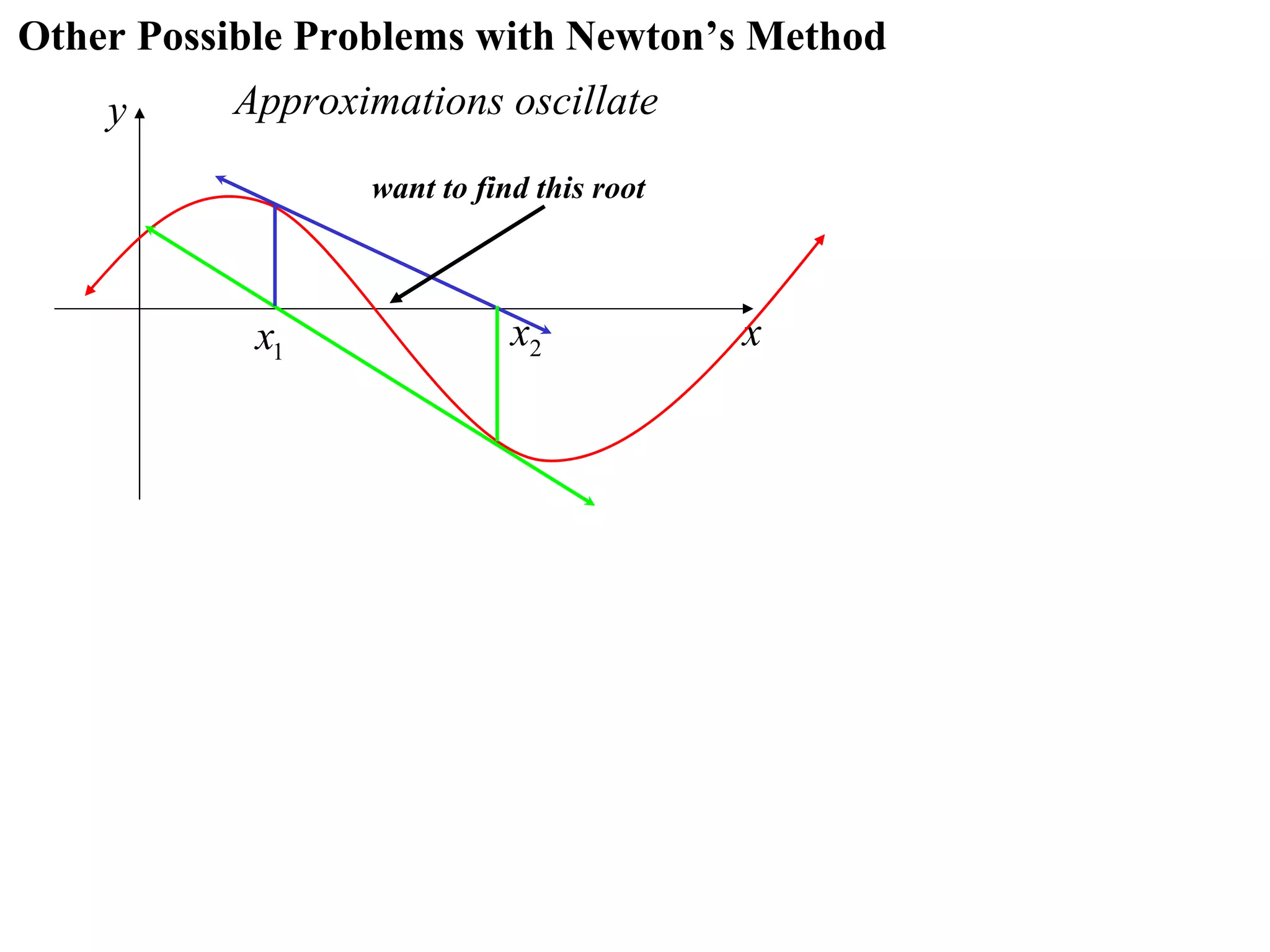
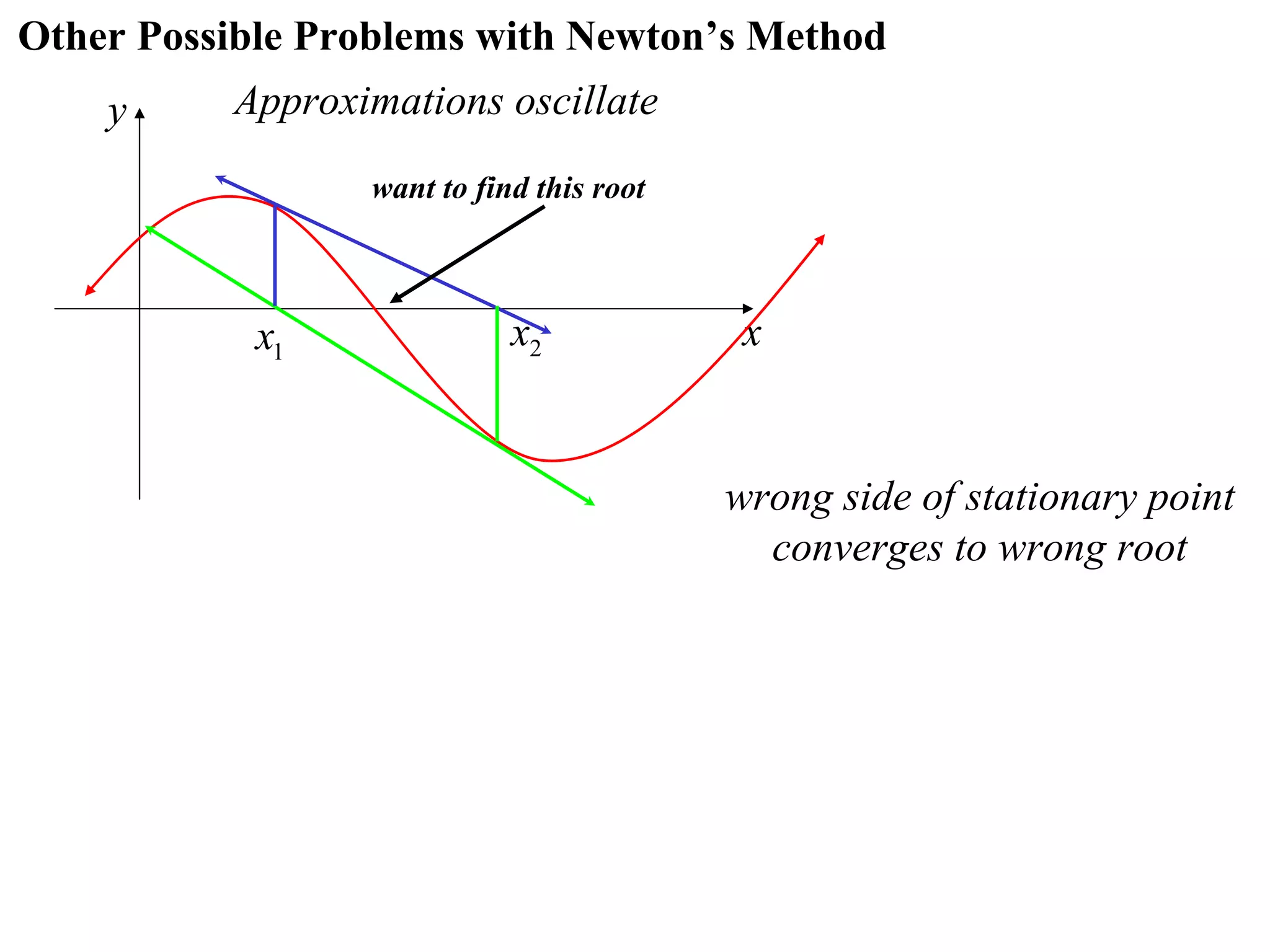
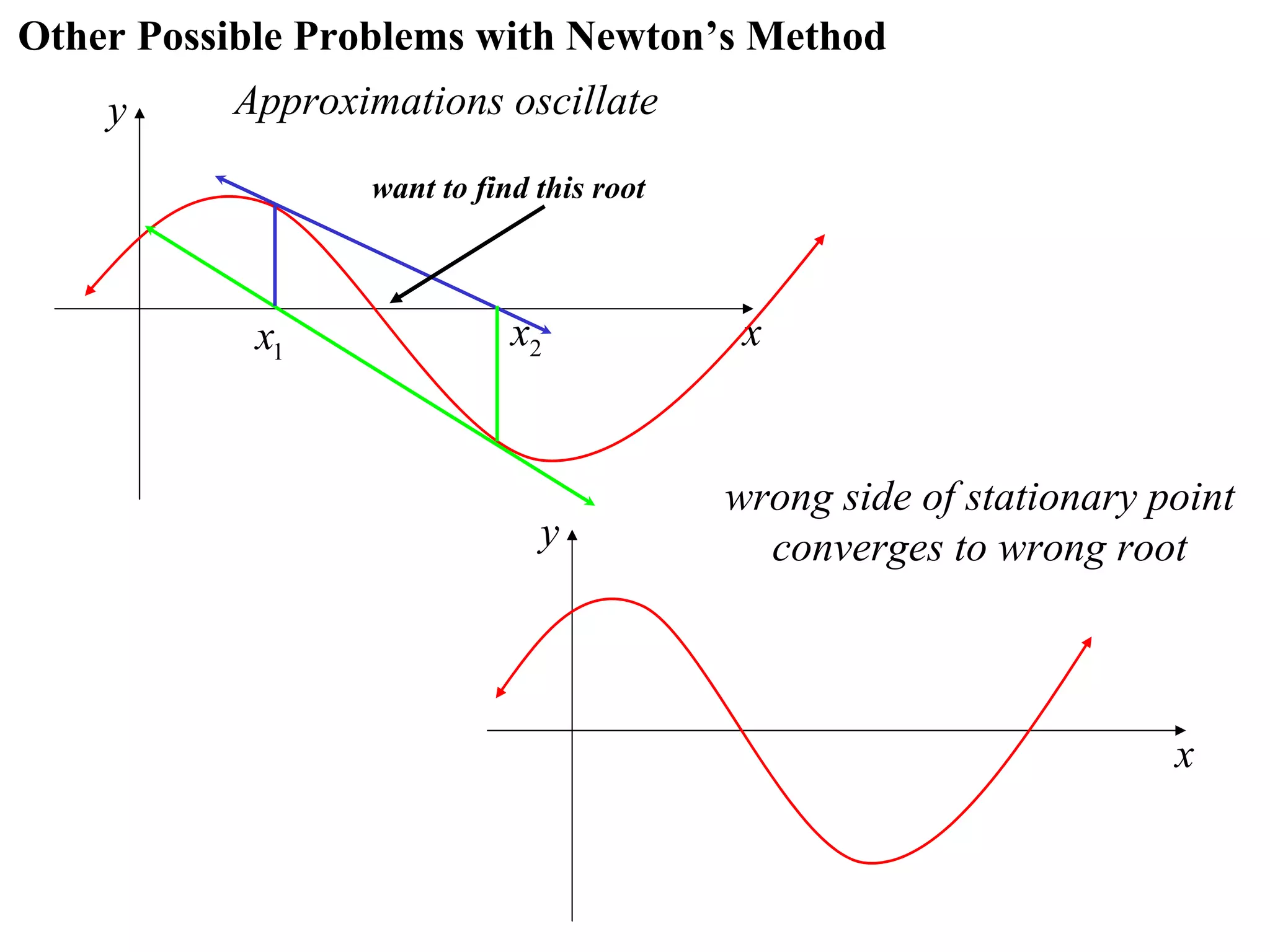
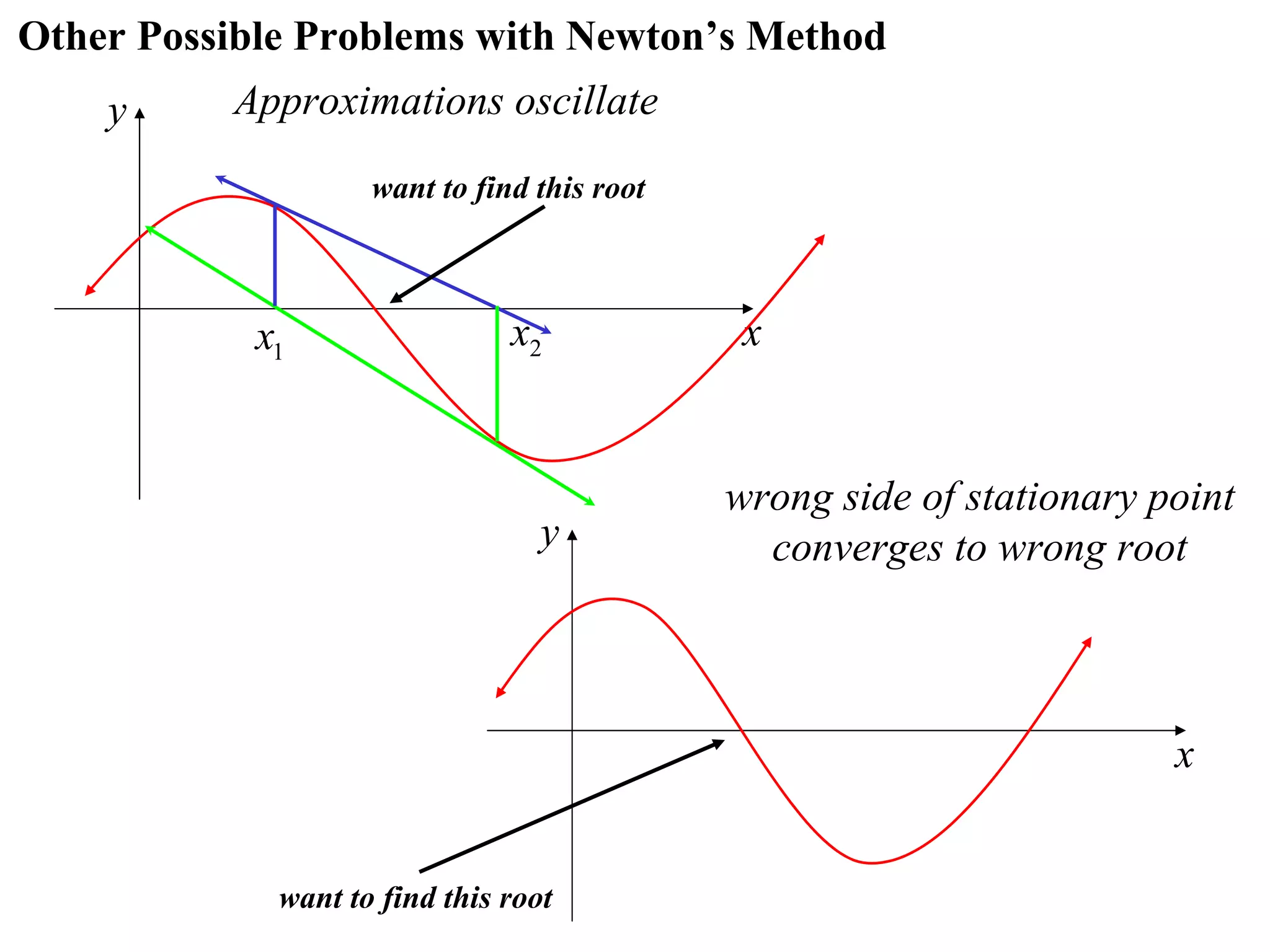
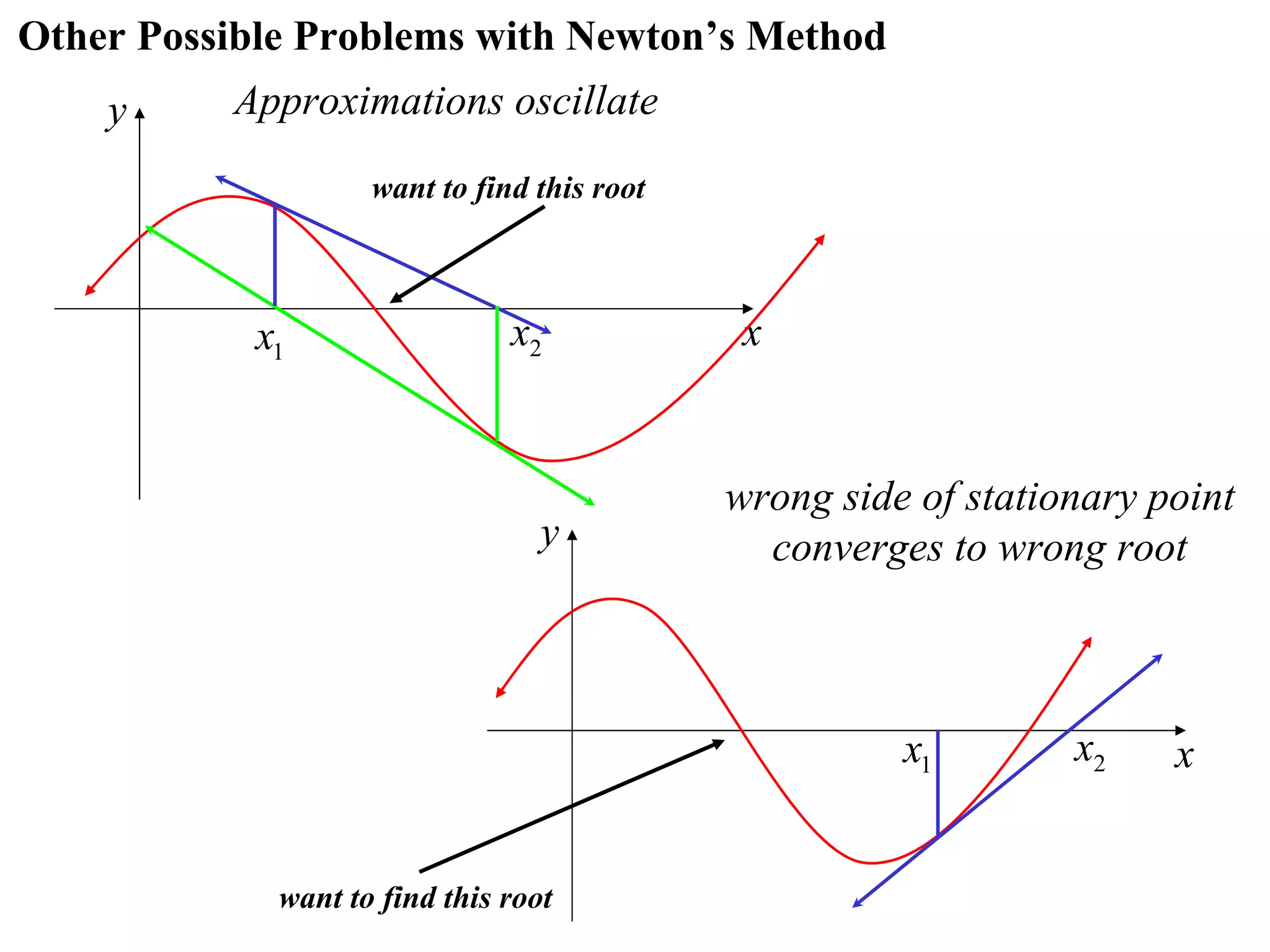
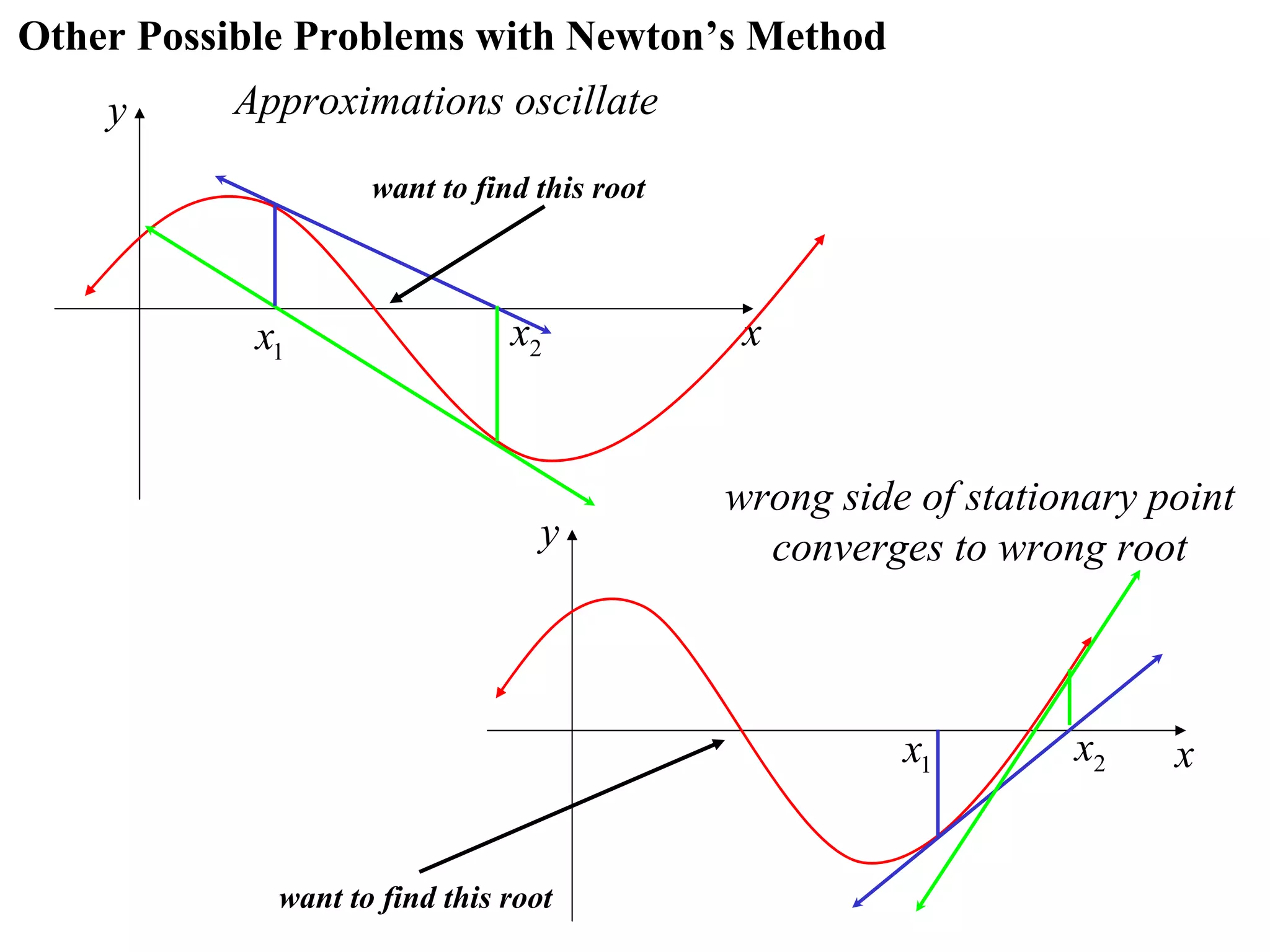
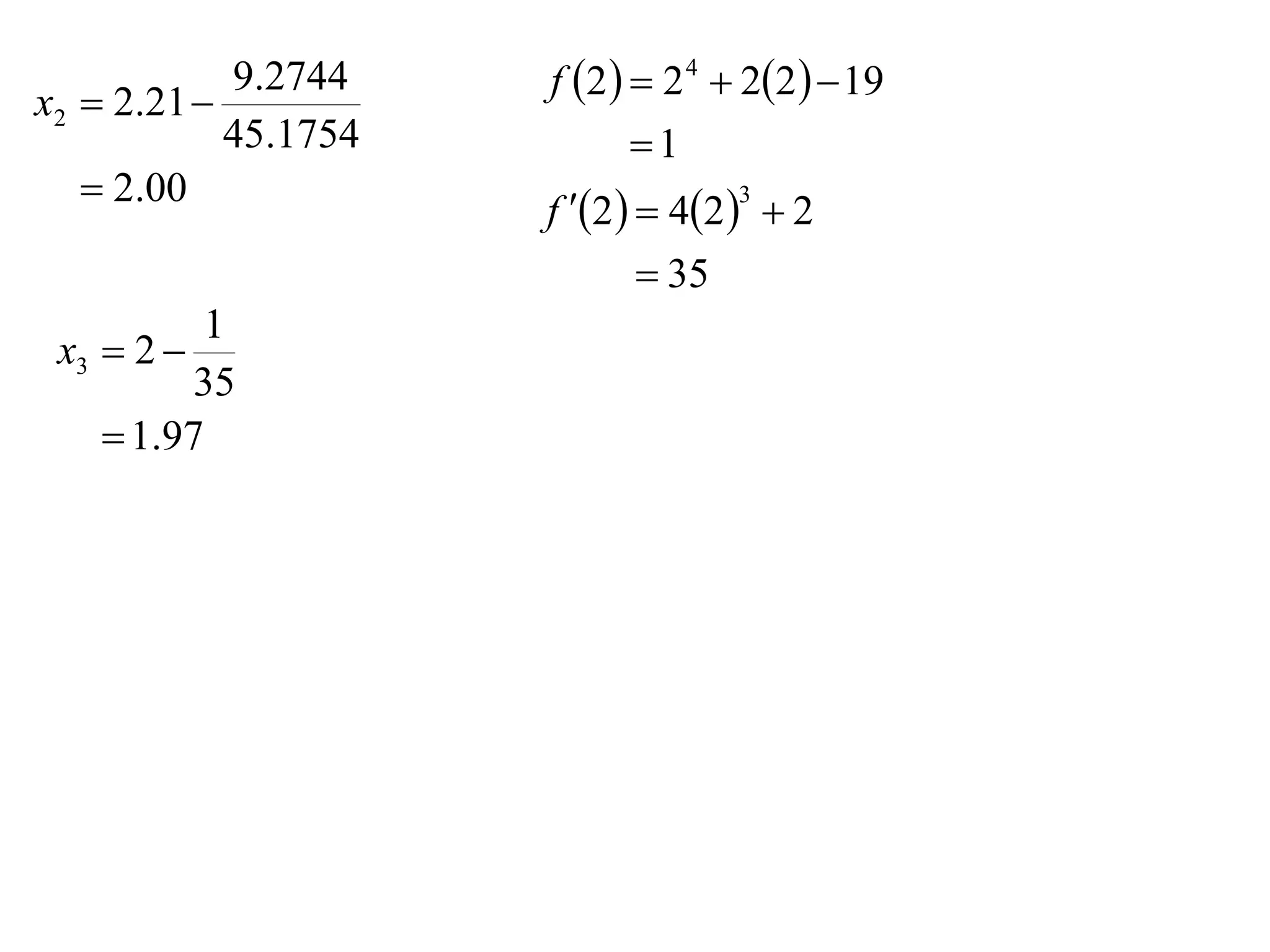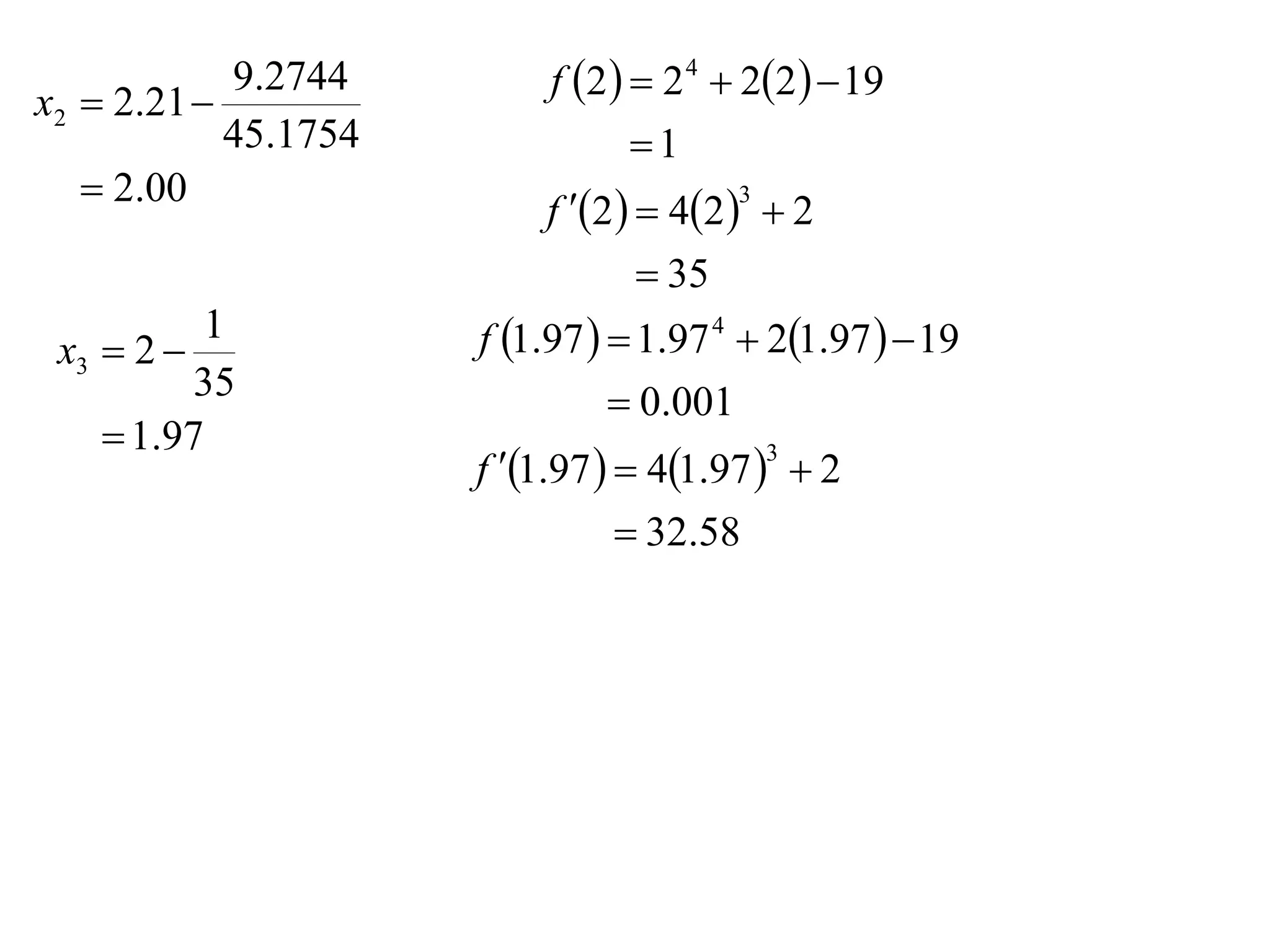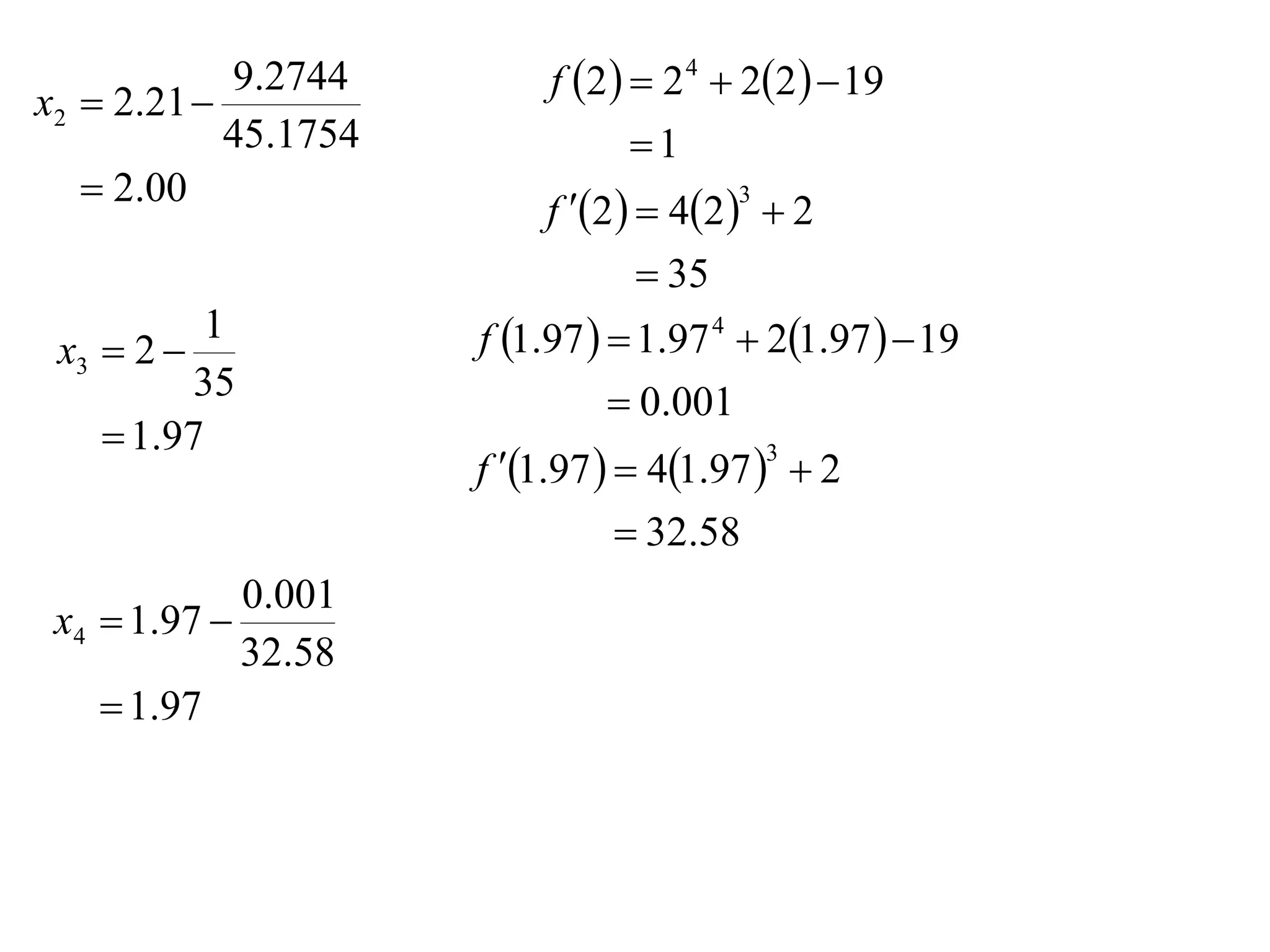The document describes the method of halving intervals to find approximations of roots. It begins by stating if a function f(x) is continuous on an interval [a,b] where f(a) and f(b) have opposite signs, then there exists a root between a and b. It then works through an example of finding the root of x4 + 2x - 19 = 0 between 1 and 3 by repeatedly halving intervals and evaluating the function at the midpoint until reaching an approximation of 1.96 to two decimal places.

1. Approximations To Roots
(1) Halving The Interval

2. Approximations To Roots
(1) Halving The Interval
y
y  f x
x
If y = f(x) is a continuous function over the interval a  x  b , and
f(a) and f(b) are opposite in sign,

3. Approximations To Roots
(1) Halving The Interval
y
y  f x
f a 
a b x
f b 
If y = f(x) is a continuous function over the interval a  x  b , and
f(a) and f(b) are opposite in sign,

4. Approximations To Roots
(1) Halving The Interval
y
y  f x
f a 
a b x
f b 
If y = f(x) is a continuous function over the interval a  x  b , and
f(a) and f(b) are opposite in sign, then at least one root of the equation
f(x) = 0 lies in the interval a  x  b

5. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3

6. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3
f  x   x 4  2 x  19 f 1  14  2  19 f 3  34  23  19
 16  0  68  0

7. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3
f  x   x 4  2 x  19 f 1  14  2  19 f 3  34  23  19
 16  0  68  0
1 3
x1  f 2   2 4  22   19
2
1 0 1 2 3
2

8. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3
f  x   x 4  2 x  19 f 1  14  2  19 f 3  34  23  19
 16  0  68  0
1 3
x1  f 2   2 4  22   19
2
1 0 1 2 3
2
 solution lies in interval 1  x  2

9. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3
f  x   x 4  2 x  19 f 1  14  2  19 f 3  34  23  19
 16  0  68  0
1 3
x1  f 2   2 4  22   19
2
1 0 1 2 3
2
 solution lies in interval 1  x  2
1 2
x2  f 1.5  1.54  21.5  19
2
 10.9  0 1 1.5 2
 1 .5

10. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0 in the interval 1  x  3
f  x   x 4  2 x  19 f 1  14  2  19 f 3  34  23  19
 16  0  68  0
1 3
x1  f 2   2 4  22   19
2
1 0 1 2 3
2
 solution lies in interval 1  x  2
1 2
x2  f 1.5  1.54  21.5  19
2
 10.9  0 1 1.5 2
 1 .5
 solution lies in interval 1.5  x  2

11. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75

12. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75
 solution lies in interval 1.75  x  2

13. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75
 solution lies in interval 1.75  x  2
1.75  2 f 1.88  1.88 4  21.88  19
x4 
2
 2.75  0 1.75 1.88 2
 1.88

14. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75
 solution lies in interval 1.75  x  2
1.75  2 f 1.88  1.88 4  21.88  19
x4 
2
 2.75  0 1.75 1.88 2
 1.88
 solution lies in interval 1.88  x  2

15. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75
 solution lies in interval 1.75  x  2
1.75  2 f 1.88  1.88 4  21.88  19
x4 
2
 2.75  0 1.75 1.88 2
 1.88
 solution lies in interval 1.88  x  2
1.88  2 f 1.94   1.94 4  21.94   19
x5 
2
 0.96  0 1.88 1.94 2
 1.94

16. 1 .5  2
x3  f 1.75  1.75 4  21.75  19
2
 6.12  0 1.5 1.75 2
 1.75
 solution lies in interval 1.75  x  2
1.75  2 f 1.88  1.88 4  21.88  19
x4 
2
 2.75  0 1.75 1.88 2
 1.88
 solution lies in interval 1.88  x  2
1.88  2 f 1.94   1.94 4  21.94   19
x5 
2
 0.96  0 1.88 1.94 2
 1.94
 solution lies in interval 1.94  x  2

17. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97

18. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97
 solution lies in interval 1.94  x  1.97

19. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97
 solution lies in interval 1.94  x  1.97
1.94  1.97
x7 
2 f 1.96   1.96 4  21.96   19
1.94 1.96 1.97
 1.96
 0.32  0

20. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97
 solution lies in interval 1.94  x  1.97
1.94  1.97
x7 
2 f 1.96   1.96 4  21.96   19
1.94 1.96 1.97
 1.96
 0.32  0
 solution lies in interval 1.96  x  1.97

21. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97
 solution lies in interval 1.94  x  1.97
1.94  1.97
x7 
2 f 1.96   1.96 4  21.96   19
1.94 1.96 1.97
 1.96
 0.32  0
 solution lies in interval 1.96  x  1.97
1.96  1.97
x8 
2
 1.97

22. 1.94  2
x6  f 1.97   1.97 4  21.97   19
2
 0.001  0 1.94 1.97 2
 1.97
 solution lies in interval 1.94  x  1.97
1.94  1.97
x7 
2 f 1.96   1.96 4  21.96   19
1.94 1.96 1.97
 1.96
 0.32  0
 solution lies in interval 1.96  x  1.97
1.96  1.97
x8 
2
 1.97
 an approximation for the root is x  1.97

23. (2) Newton’s Method of Approximation

24. (2) Newton’s Method of Approximation
y
x

25. (2) Newton’s Method of Approximation
y
x
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 

26. (2) Newton’s Method of Approximation
y
x
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 
Successive approximations x2 , x3 ,  , xn , xn 1are given by;
f  xn 
xn 1  xn 
f  xn 

27. NOTE:
(2) Newton’s Method of Approximation
y x0 must be a good first
approximation
Newton’s method finds
where the tangent at x0
cuts the x axis
x
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 
Successive approximations x2 , x3 ,  , xn , xn 1are given by;
f  xn 
xn 1  xn 
f  xn 

28. NOTE:
(2) Newton’s Method of Approximation
y x0 must be a good first
approximation
y  f x Newton’s method finds
where the tangent at x0
cuts the x axis
x0 x
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 
Successive approximations x2 , x3 ,  , xn , xn 1are given by;
f  xn 
xn 1  xn 
f  xn 

29. NOTE:
(2) Newton’s Method of Approximation
y x0 must be a good first
approximation
y  f x Newton’s method finds
where the tangent at x0
cuts the x axis
x1 x0 x
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 
Successive approximations x2 , x3 ,  , xn , xn 1are given by;
f  xn 
xn 1  xn 
f  xn 

30. NOTE:
(2) Newton’s Method of Approximation
y x0 must be a good first
approximation
y  f x Newton’s method finds
where the tangent at x0
cuts the x axis
x1 x0 x If f  x0   0
i.e. tangent || x axis
the method will fail
If x0 is a good first approximation to a root of the equation f(x) = 0,
then a closer approximation is given by;
f  x0 
x1  x0 
f  x0 
Successive approximations x2 , x3 ,  , xn , xn 1are given by;
f  xn 
xn 1  xn 
f  xn 

31. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0

32. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0
f  x   x 4  2 x  19
f  x   4 x 3  2

33. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0
f  x   x 4  2 x  19
f  x   4 x 3  2
x0  1.5 f 1.5  1.54  21.5  19 f 1.5  41.53  2
 10.9375  15.5

34. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0
f  x   x 4  2 x  19
f  x   4 x 3  2
x0  1.5 f 1.5  1.54  21.5  19 f 1.5  41.53  2
 10.9375  15.5
f  x0 
x1  x0 
f  x0 
 10.9375
 1 .5 
15.5
 2.21

35. e.g Find an approximation to two decimal places for a root of
x 4  2 x  19  0
f  x   x 4  2 x  19
f  x   4 x 3  2
x0  1.5 f 1.5  1.54  21.5  19 f 1.5  41.53  2
 10.9375  15.5
f  x0 
x1  x0  f 2.21  2.214  22.21  19
f  x0 
 9.2744
 10.9375
 1 .5  f 2.21  42.21  2
3
15.5
 2.21  45.1754

36. 9.2744
x2  2.21 
45.1754
 2.00

37. 9.2744 f 2   2 4  22   19
x2  2.21 
45.1754 1
 2.00
f 2   42   2
3
 35

38. 9.2744 f 2   2 4  22   19
x2  2.21 
45.1754 1
 2.00
f 2   42   2
3
 35
1
x3  2 
35
 1.97

39. 9.2744 f 2   2 4  22   19
x2  2.21 
45.1754 1
 2.00
f 2   42   2
3
 35
x3  2 
1 f 1.97   1.97 4  21.97   19
35  0.001
 1.97
f 1.97   41.97   2
3
 32.58

40. 9.2744 f 2   2 4  22   19
x2  2.21 
45.1754 1
 2.00
f 2   42   2
3
 35
x3  2 
1 f 1.97   1.97 4  21.97   19
35  0.001
 1.97
f 1.97   41.97   2
3
 32.58
0.001
x4  1.97 
32.58
 1.97

41. 9.2744 f 2   2 4  22   19
x2  2.21 
45.1754 1
 2.00
f 2   42   2
3
 35
x3  2 
1 f 1.97   1.97 4  21.97   19
35  0.001
 1.97
f 1.97   41.97   2
3
 32.58
0.001
x4  1.97 
32.58
 1.97
 x  1.97 is a better approximation for the root

42. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places

43. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
f  x   x 2  23

44. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
f  x   x 2  23
f  x  2x

45. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
xn12  23
f  x   x  23
2
xn  xn1 
2 xn1
f  x  2x
xn12  23

2 xn1

46. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
xn12  23
f  x   x  23
2
xn  xn1 
2 xn1
f  x  2x
xn12  23

2 xn1
x0  5

47. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
xn12  23
f  x   x  23
2
xn  xn1 
2 xn1
f  x  2x
xn12  23

2 xn1
x0  5
52  23
x1 
2 5
x1  4.8

48. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
xn12  23
f  x   x  23
2
xn  xn1 
2 xn1
f  x  2x
xn12  23

2 xn1
x0  5
52  23 4.82  23
x1  x2 
2 5 2  4.8 
x1  4.8 x2  4.795833333
x2  4.80 (to 2 dp)

49. (ii ) Use Newton's Method to obtain an approximation to 23
correct to two decimal places
xn12  23
f  x   x  23
2
xn  xn1 
2 xn1
f  x  2x
xn12  23

2 xn1
x0  5
52  23 4.82  23
x1  x2 
2 5 2  4.8 
x1  4.8 x2  4.795833333
x2  4.80 (to 2 dp)
 23  4.80 (to 2 dp)

50. Other Possible Problems with Newton’s Method

51. Other Possible Problems with Newton’s Method
Approximations oscillate

52. Other Possible Problems with Newton’s Method
y Approximations oscillate
x

53. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x

54. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x

55. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x

56. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x
wrong side of stationary point
converges to wrong root

57. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x
wrong side of stationary point
y converges to wrong root
x

58. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x
wrong side of stationary point
y converges to wrong root
x
want to find this root

59. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x
wrong side of stationary point
y converges to wrong root
x1 x2 x
want to find this root

60. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
x1 x2 x
wrong side of stationary point
y converges to wrong root
x1 x2 x
want to find this root

61. Other Possible Problems with Newton’s Method
y Approximations oscillate
want to find this root
Exercise 6E; 1, 3ac,
6adf, 8a, 10, 12
x1 x2 x
wrong side of stationary point
y converges to wrong root
x1 x2 x
want to find this root