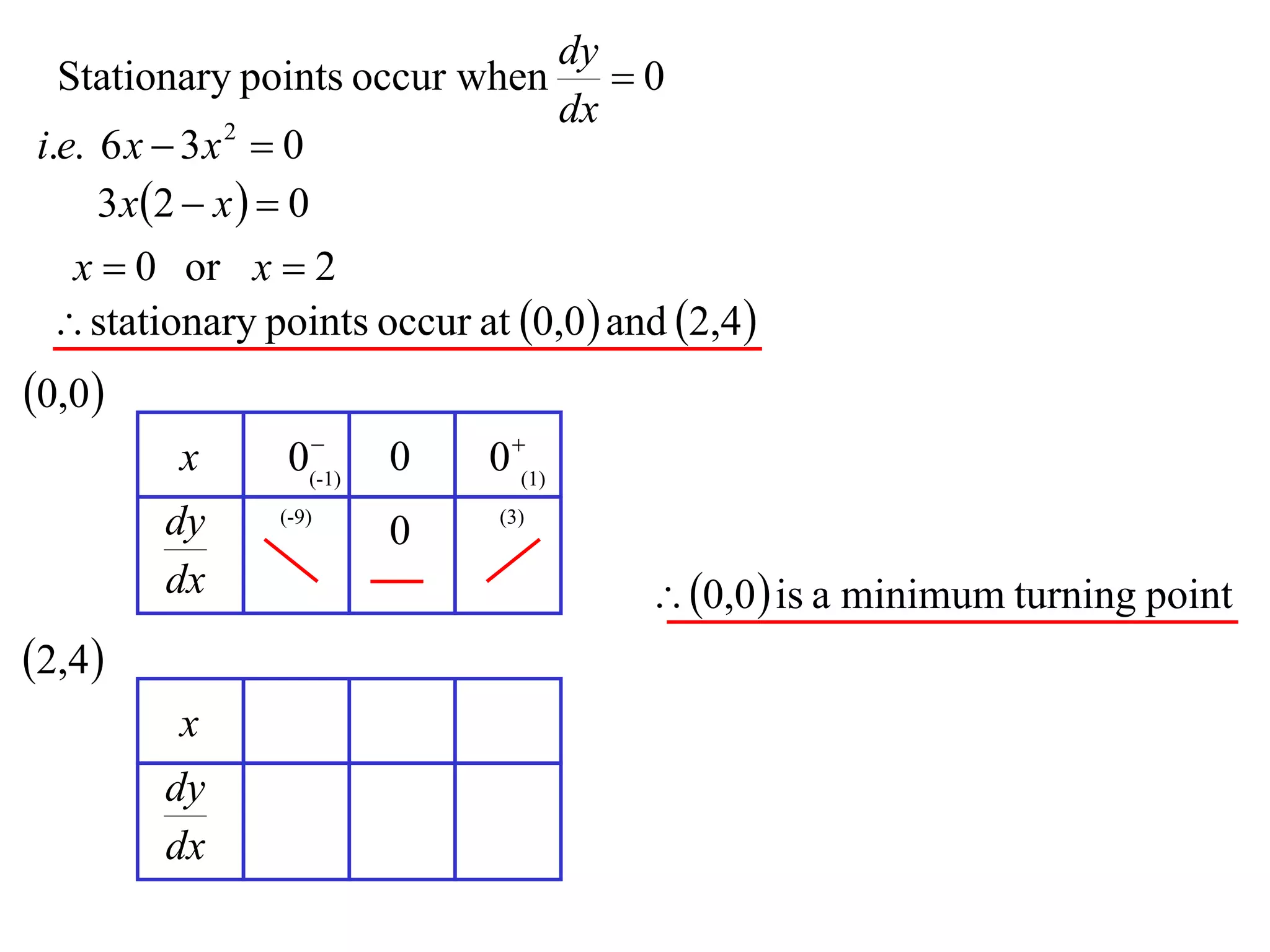
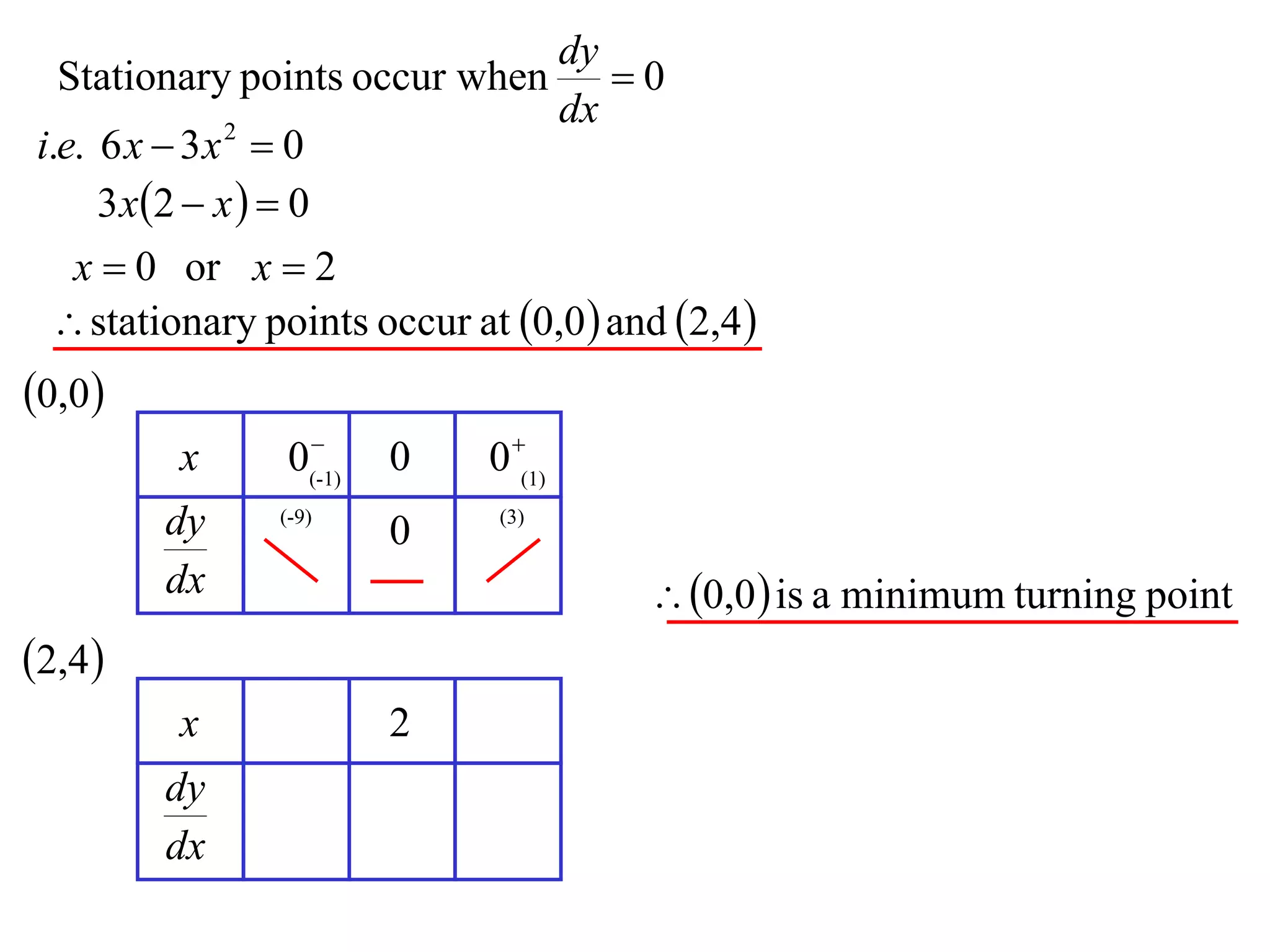
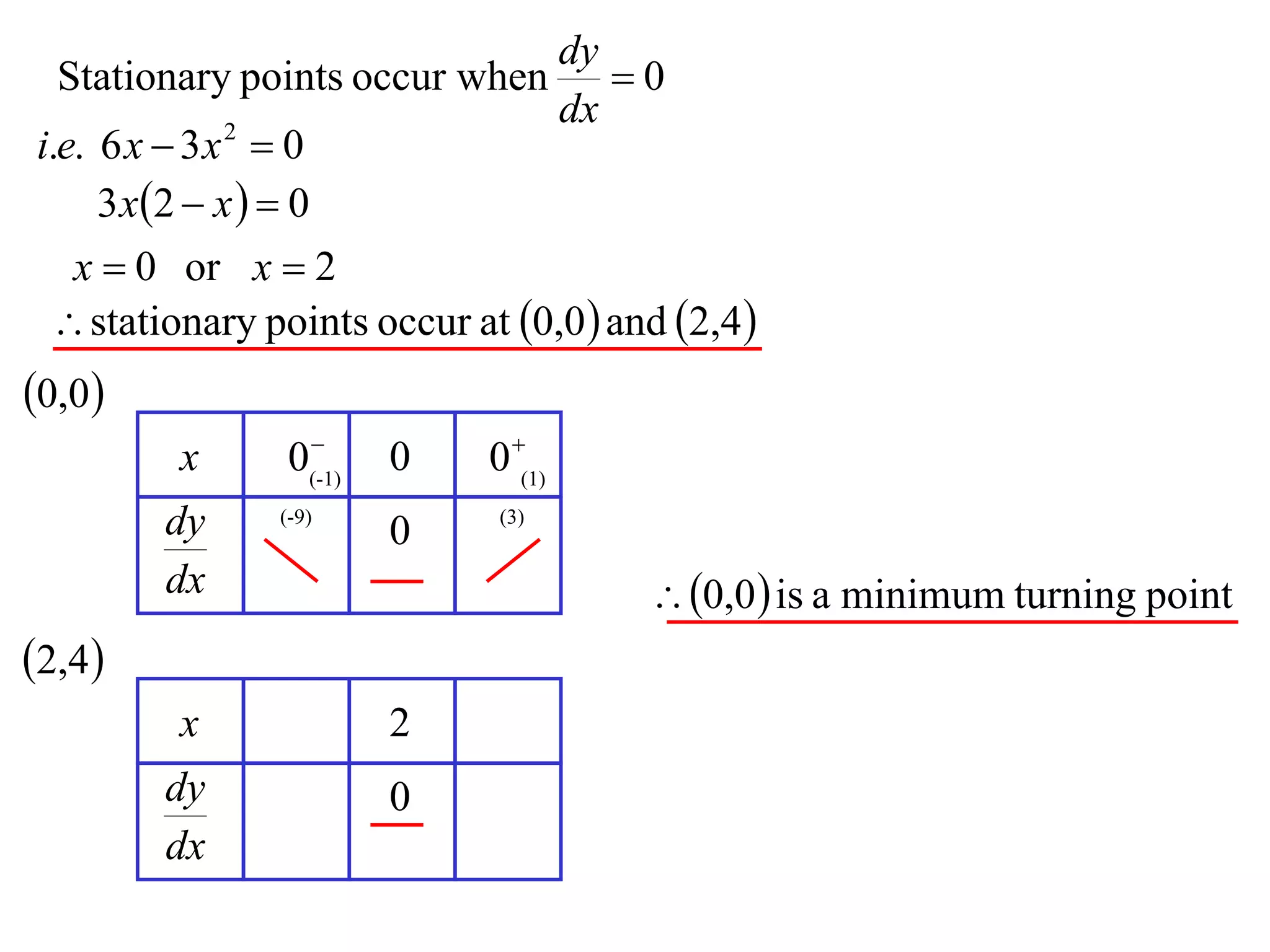
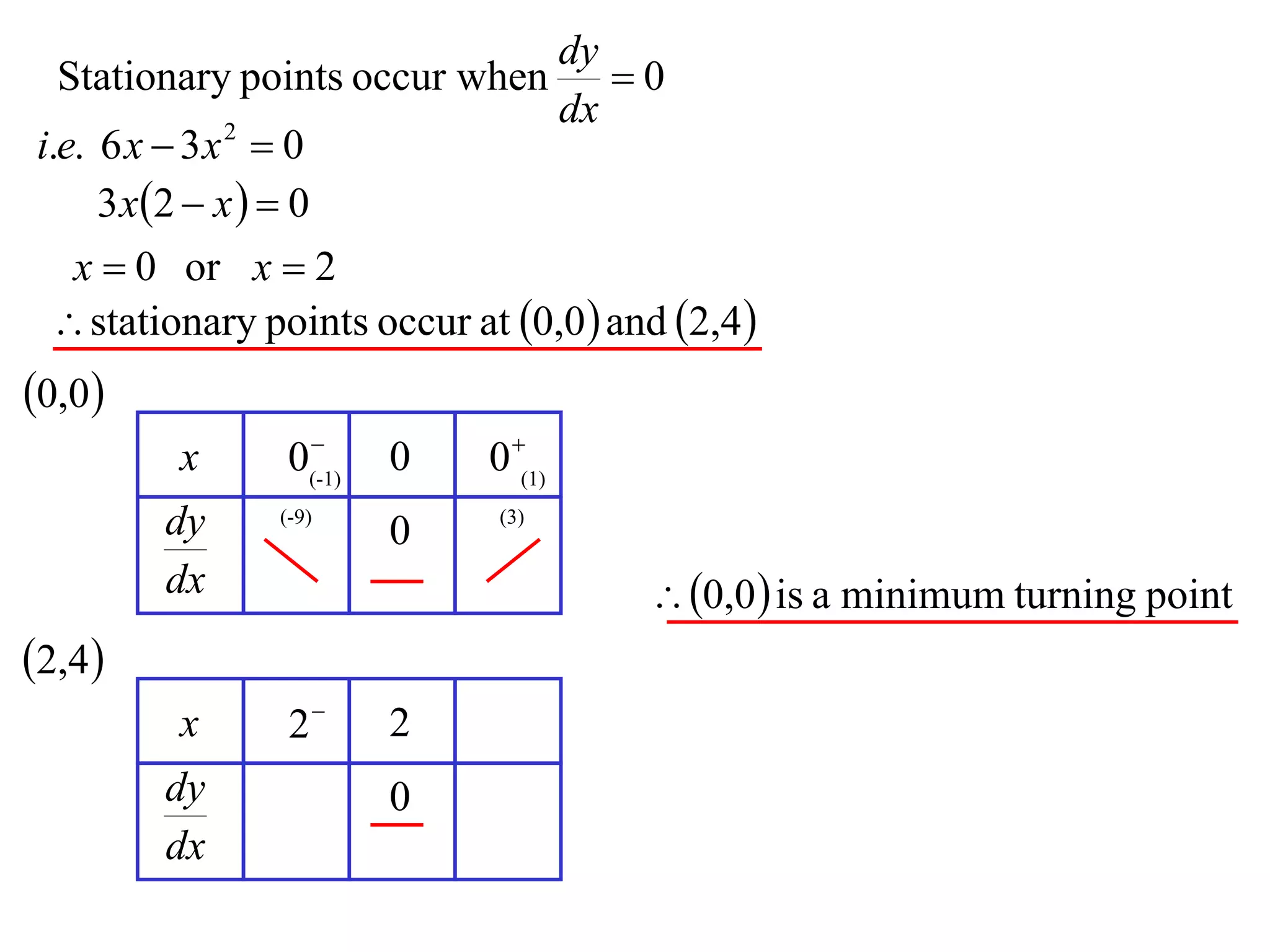
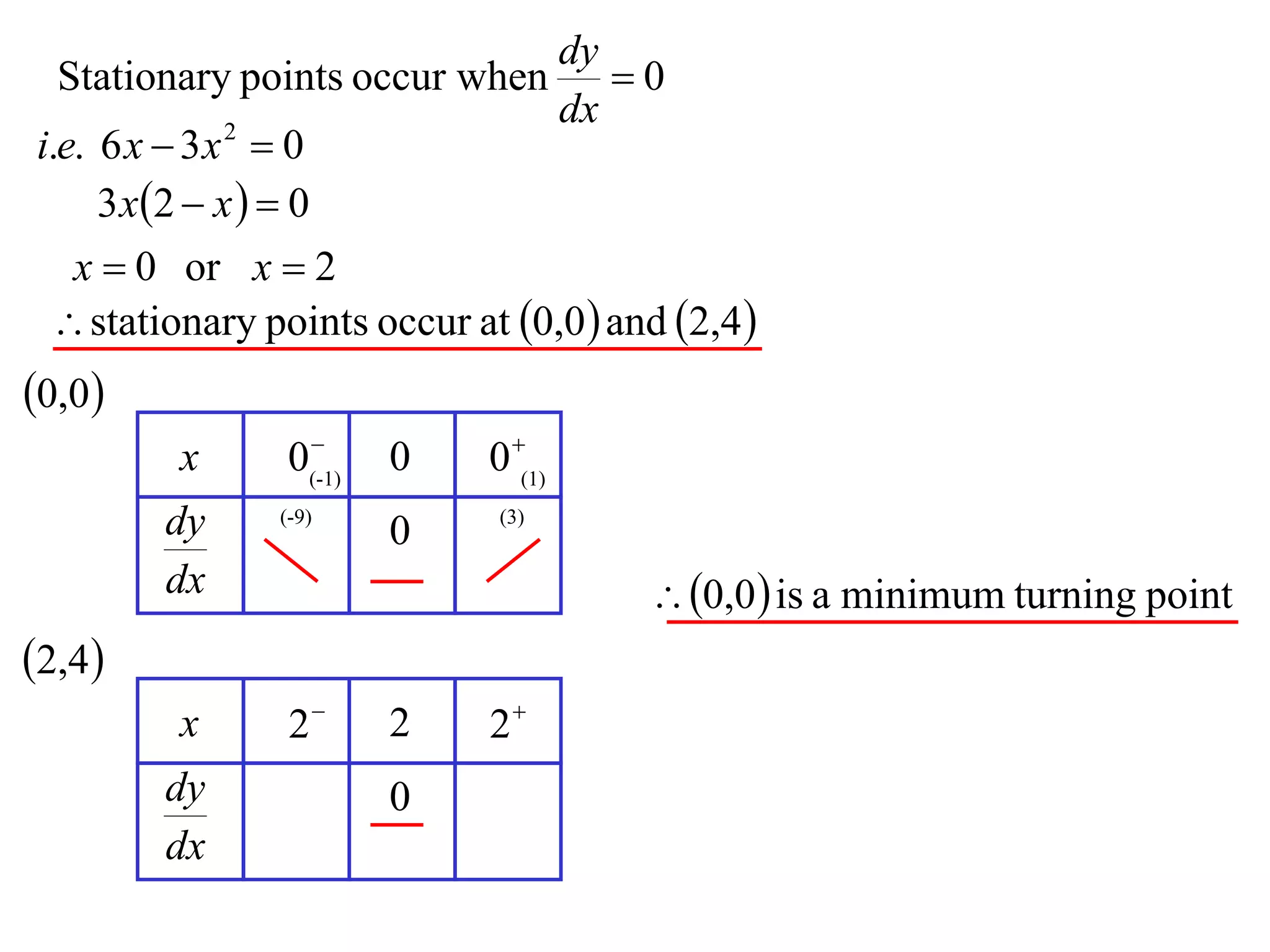
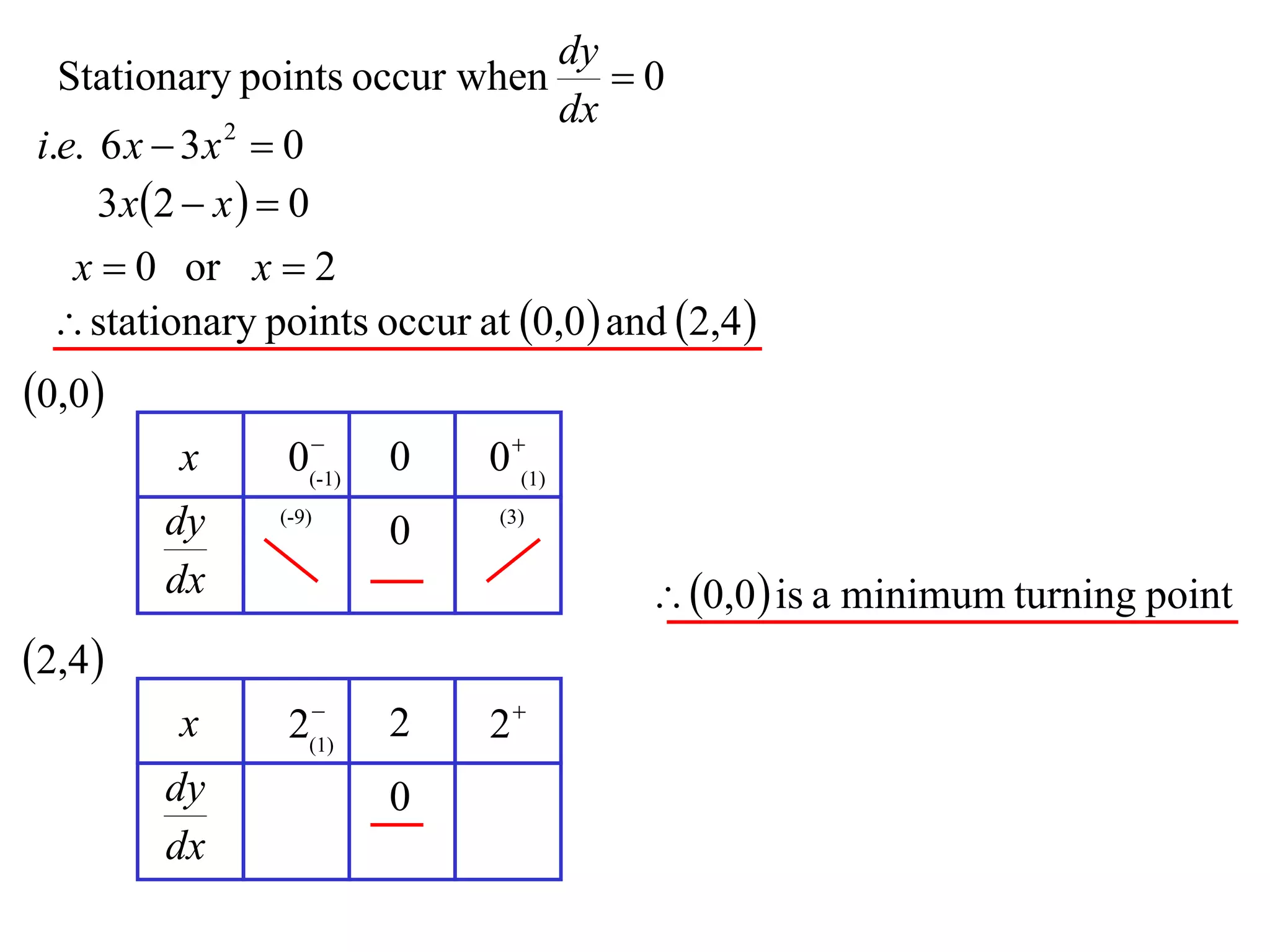
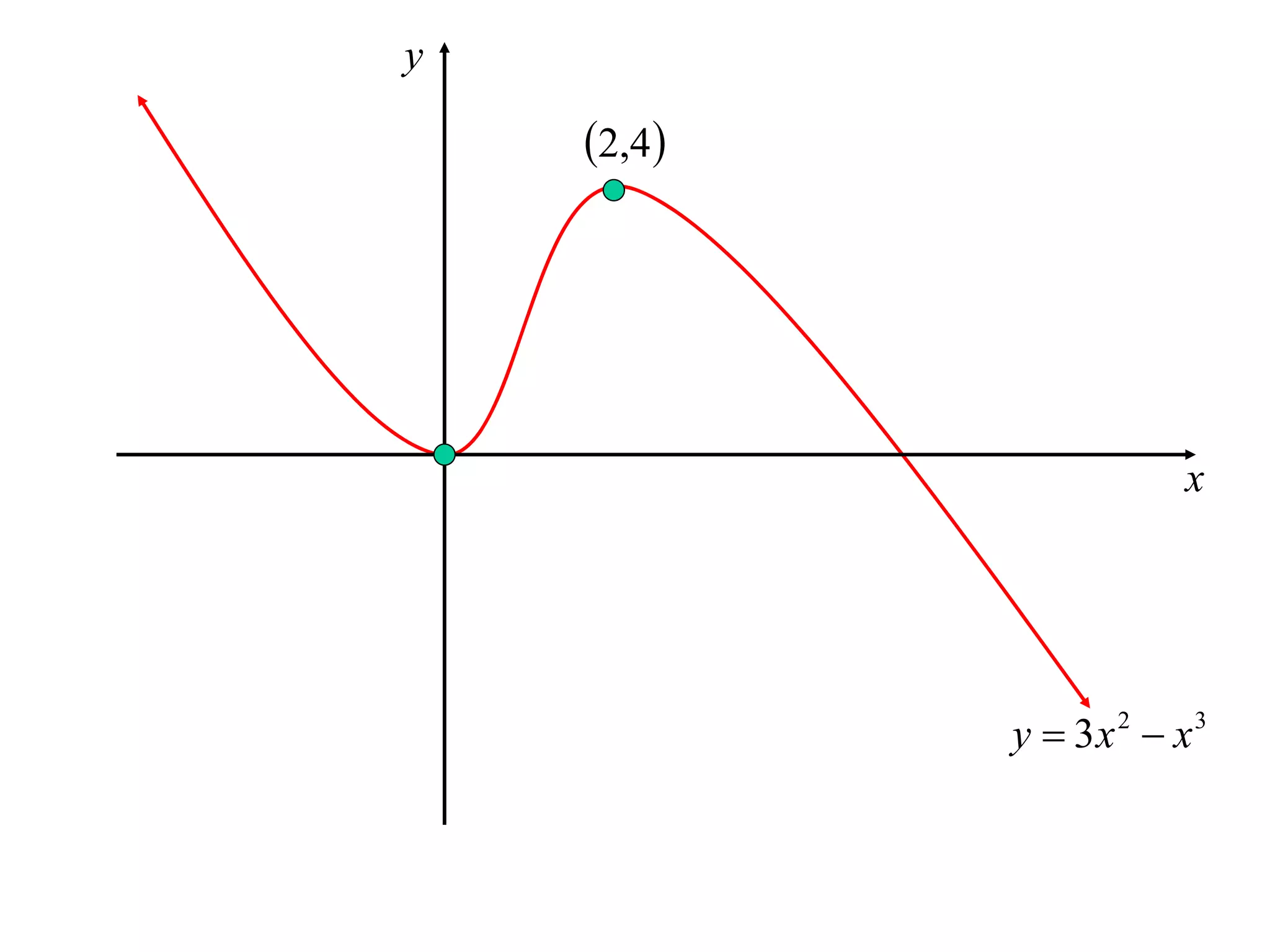
The document discusses the use of derivatives to analyze curves geometrically. It states that the derivative measures the slope of the tangent line to a curve. If the derivative is positive, the curve is increasing; if negative, decreasing; if zero, the curve is stationary. For the example curve y = 3x^2 - x^3, it finds the stationary points at (0,0) and (2,4) by setting the derivative equal to zero. It determines that (0,0) is a minimum turning point and (2,4) is a stationary point.

1. Geometrical Applications
of Differentiation
The First Derivative

2. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx

3. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx

4. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx
If f  x   0, the curve is increasing

5. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx
If f  x   0, the curve is increasing
If f  x   0, the curve is decreasing

6. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx
If f  x   0, the curve is increasing
If f  x   0, the curve is decreasing
If f  x   0, the curve is stationary

7. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx
If f  x   0, the curve is increasing
If f  x   0, the curve is decreasing
If f  x   0, the curve is stationary
e.g. For the curve y  3 x 2  x 3 , find all of the stationary points
and determine their nature.
Hence sketch the curve

8. Geometrical Applications
of Differentiation d dy
The First Derivative y, f  x ,  f  x ,
dx dx
dy
measures the slope of the tangent to a curve
dx
If f  x   0, the curve is increasing
If f  x   0, the curve is decreasing
If f  x   0, the curve is stationary
e.g. For the curve y  3 x 2  x 3 , find all of the stationary points
and determine their nature.
Hence sketch the curve
dy
 6 x  3x 2
dx

9. dy
Stationary points occur when  0
dx

10. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2

11. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2

12. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 

13. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

14. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0
x
dy
dx

15. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0
x 0
dy
dx

16. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0
x 0
dy 0
dx

17. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0
x 0 0
dy 0
dx

18. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0
x 0 0 0
dy 0
dx

19. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0
dy 0
dx

20. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0
dy (-9)
0
dx

21. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0
dx

22. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx

23. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point

24. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

25. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4
x
dy
dx

26. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4
x 2
dy
dx

27. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4
x 2
dy 0
dx

28. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4
x 2 2
dy 0
dx

29. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4
x 2 2 2
dy 0
dx

30. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

x 2(1) 2 2
dy 0
dx

31. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

x 2(1) 2 2
dy (3)
0
dx

32. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

x 2(1) 2 2 (3)
dy (3)
0
dx

33. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

x 2(1) 2 2 (3)
dy (3)
0 (-9)
dx

34. dy
Stationary points occur when  0
dx
i.e. 6 x  3 x  0
2
3 x 2  x   0
x  0 or x  2
 stationary points occur at 0,0  and 2,4 
0,0

x 0(-1) 0 0 (1)
dy (-9)
0 (3)
dx  0,0  is a minimum turning point
2,4

x 2(1) 2 2 (3)
dy (3)
0 (-9)
dx  2,4  is a maximum turning point

35. y
x

36. y
x

37. y
2,4
x

38. y
2,4
x
y  3x 2  x 3

39. Exercise 10A; 1, 2ace, 4, 5, 6ac, 7, 8, 9ace etc,
11, 12, 13, 15ace, 16, 17
Exercise 10B; 1ad, 2ac, 3ac, 5, 6, 7ac, 8, 10, 12