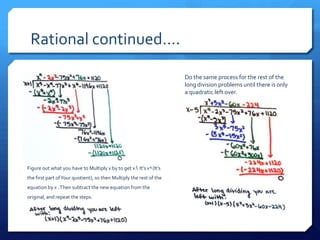
The document summarizes reflections from Patrick Hyatt and Quincie McCalla on a project where they created complex math problems to review concepts they had learned. Both note that while the project provided some review, it took a significant amount of time to develop the problems and stretched their understanding too far at times. They suggest modifying the format of the project to have students work in pairs and take responsibility for specific concepts, then present problems to each other, for a more focused review that clarifies misunderstandings.

1. Developing Expert Voice
Patrick Hyatt and Quincie McCalla
The Sexy Simplifiers

2. Cubic Conundrum
Solve for “x”, given: x = -5
3 2 5 4 3 2
 PROBLEM: x +4x -7x -10 x +6x -2x -36x + x +30
 Solution:
 Step 1: Long divide
Figure out what you have to Multiply x 3 to get x 5.
It’s x2(first part of Your quotient), so then Multiply
the rest of the polynomial by x2 Then subtract
.
the new polynomial from the original, and repeat
the steps.

3. Cubic Conundrum continued…
Solve for “x”, given: x = -5
3 2 5 4 3 2
 PROBLEM: x +4x -7x -10 x +6x -2x -36x + x +30
 Solution:
 Step 2: Long divide with x+5 (you were given it)
Factor by
finding the
multiples of “c”
that add up to
“b”. (ax+bx+c)
Solve for “x” by setting each factor equal to zero
X= -5, 2, -1, -3, 1

4. LOGs “lets hit each other with them!”
log x2- 4(x+2) + log x2- 4(x-2) + log x2- 4(x+4) = 2 SOLVE FOR “X”
Simplify the log. Log x + log x = log (x)(x)
Find greatest common factor, in this case “x”
and factor it out.
Change the log into an exponential.
Take the log base
and set it to the
power of what
the log is equal to. Then factor by grouping.
Turn in to standard form by
multiplying out the factors.
Set the formula equal to zero.

5. LOG continued…
log x2- 4(x+2) + log x2- 4(x-2) + log x2- 4(x+4) = 2 SOLVE FOR “X”
Simplify the , then plug it back into the problem.
Factor out a “-1” so the “a” value is positive.
(ax+bx+c) = standard form
Then use difference in squares:
2 2
a – b = (a + b)(a – b)
Then plug it back into the problem.
Solve for “x” by setting it equal to zero.

6. Funception
We put in each equation one at a
time, replacing “x”, so you could
see each step.

7. Funception
Cross off the equal values and simplify.
This is what's left over.
Combine like terms, distribute the 3,
And combine like terms again.
Next you multiply what is
Inside the parentheses.
You are left with…

8. Funception
Multiply both sides by 5 to get
rid of the denominator.
Factor the remaining quadratic.
Factor by finding the multiples
of -8 that add up to 2.
Solve for “x” by setting the
factor equal to zero.

9. MY rational > your rational
 Solve for “x”, graph and give the domain.
Now you can set the polynomial
equal to zero.
First, you have to make all the denominators equal.
To do this you have to find a common denominator
that all of them can go into. In this case it is 7x 2
.
Multiply each fraction by the faction that will make
You are left with this polynomial
the denominator equal to 7x .
2 and to solve you must long divide
using the x-values you were given.
Now that all of the denominators are equal you
2
can multiply both sides by 7x . And cancel out all
of the denominators.

10. Rational continued….
Do the same process for the rest of the
long division problems until there is only
a quadratic left over.
Figure out what you have to Multiply x by to get x 5. It’s x 4 (It’s
the first part of Your quotient), so then Multiply the rest of the
equation by x . Then subtract the new equation from the
original, and repeat the steps.

11. Rational never ending….
Long divide one last time. To finish find the x-intercepts by setting it equal t zero.
Now graph!
(keep in mind that this is an odd powered polynomial)
State the domain by telling where the graph is positive.
Factor by finding factors of -32 that add up to -4.

12. Long Division, difficulty: 5/5
Solve for “x”, graph, and find the domain, given: x = 2, -5, -3
Figure out what you have to Multiply x by to get x 5. It’s x 4 (It’s
the first part of Your quotient), so then Multiply the rest of the
equation by x . Then subtract the new equation from the
original, and repeat the steps.
Continue using the
same methods for long
diving the rest of the
problem.

13. Long Division, difficulty: 5/5
Solve for “x”, graph, and find the domain, given: x = 2, -5, -3
Continue to long divide. Solve for “x” by setting the
factors equal to zero.
Graph using the
x-intercepts, degree, and whether it
is positive or negative.
After all the long division you are left with. The domain of this
polynomial is when
the graph is positive
Which can be simplified to…. because you cannot
take a square root of
a negative.

14. Patrick’s Reflection
I chose the concepts of the problems I created because I already knew the
material. I did not pick a concept that I did not understand well. However, by
making the problems very complex, I ended up using the skills I needed practice
with. This helped me review the things I learned this trimester. For the sake of
review, this project worked well, but I did not get review on the concepts I really
need to. This is because I used the concepts I understood fully for the
problems. I would rather review all the concepts I need reinforcement on
instead of doing hours of busy work. Figuring out how to create a problem that
works took a majority of the time. Rather than taking my time to show you
what I know, I had to learn an almost useless skill. I suggest changing the
format of the entire project. Set up as follows: 1) groups of 2, or 1 person if
need be. 2) combined the pair has to have a problem for each unit. 3) divvy up
the problems between the pair. For simplicity lets say P1 takes unit A,B, and
C, and P2 takes unit D, E, and F. 4) P1 makes unit A, B, and C problems and
presents unit D, E, and F problems that P2 made. Visa versa. 5) present them in
class. This will give everyone a lot of review and if they do something wrong you
can clarify the issue.

15. Quincie’s Reflection
We chose our problems based on what we knew and what we could make more complicated
and still understand. The problems we chose expanded what we already knew and made us
look deeper into the inner workings of each unit. The problems we chose show that we know
more than what we were taught and that we can apply what we learned. This assignment took
forever and was a lot of time just brain storming what to do. I learned that I will never be a
math teacher because it is extremely complicated to come up with problems that work. It is
much harder to come up with a problem that works than it is to solve it. I got a little bit of
knowledge from this project. This project was good for review but I still didn't understand
everything. I learned that it takes a lot more than just solving problems to truly understand
how each unit woks. However, this project also confused me. It made me second guess what I
learned and made it very difficult to do. It stretched my brain a little too far at times. Over all I
learned quite a bit from this assigned. The only thing I would recommend is to make the
project a little less open ended. I almost didn't know where to start and it was frustrating. I
think that there is a way to do this project that will make it more enjoyable. It was. Little too
time consuming and tedious.