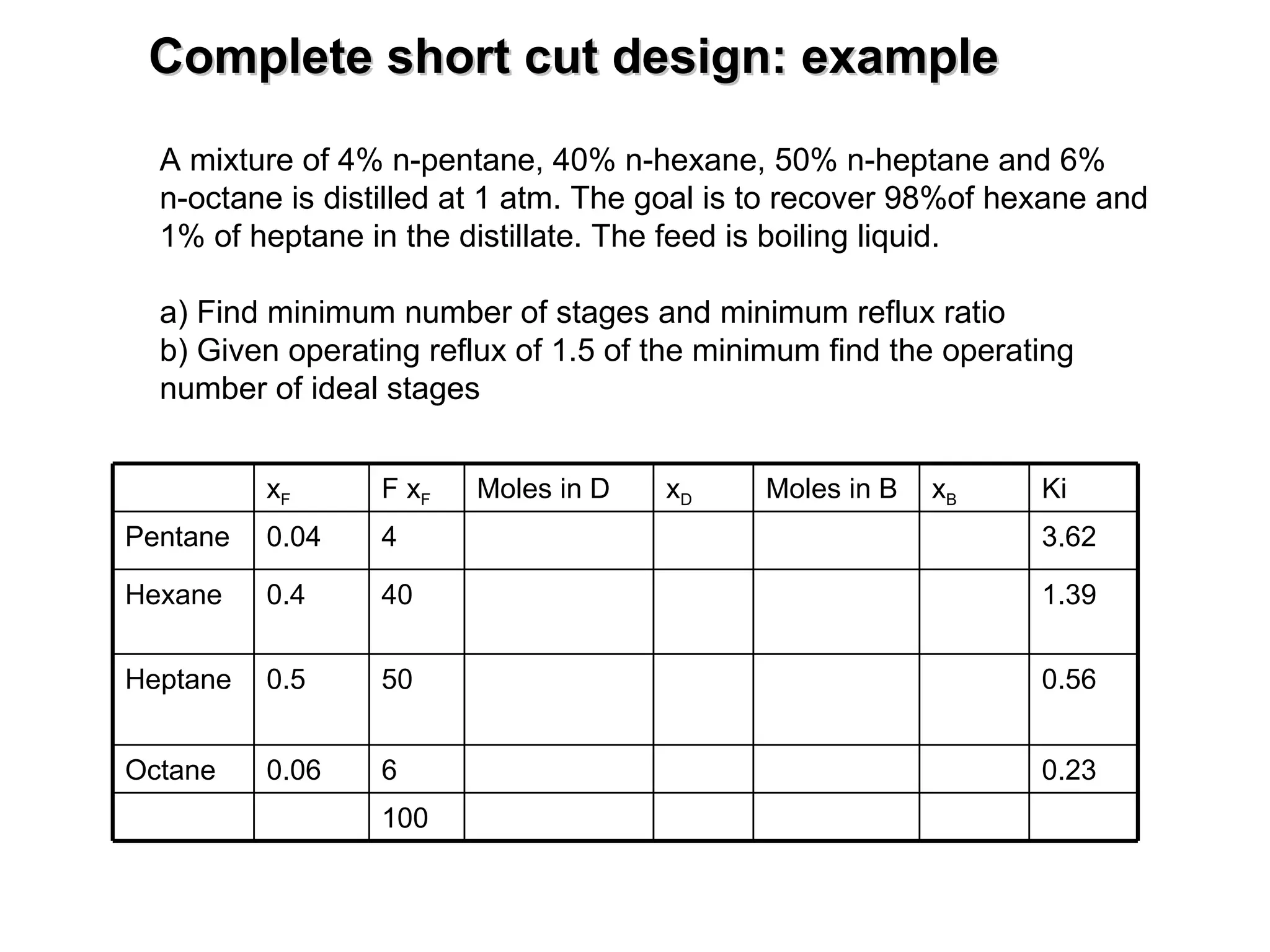
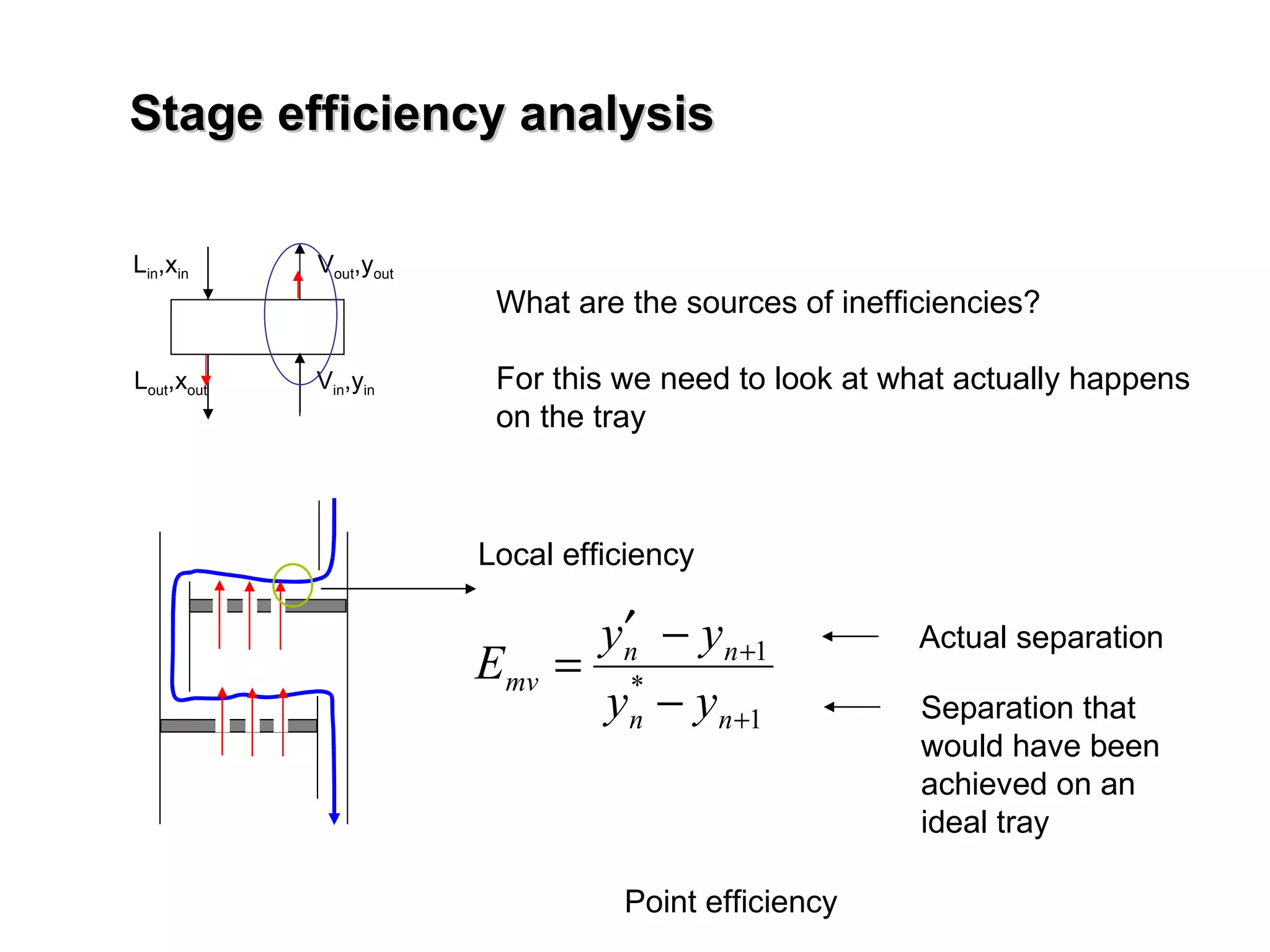
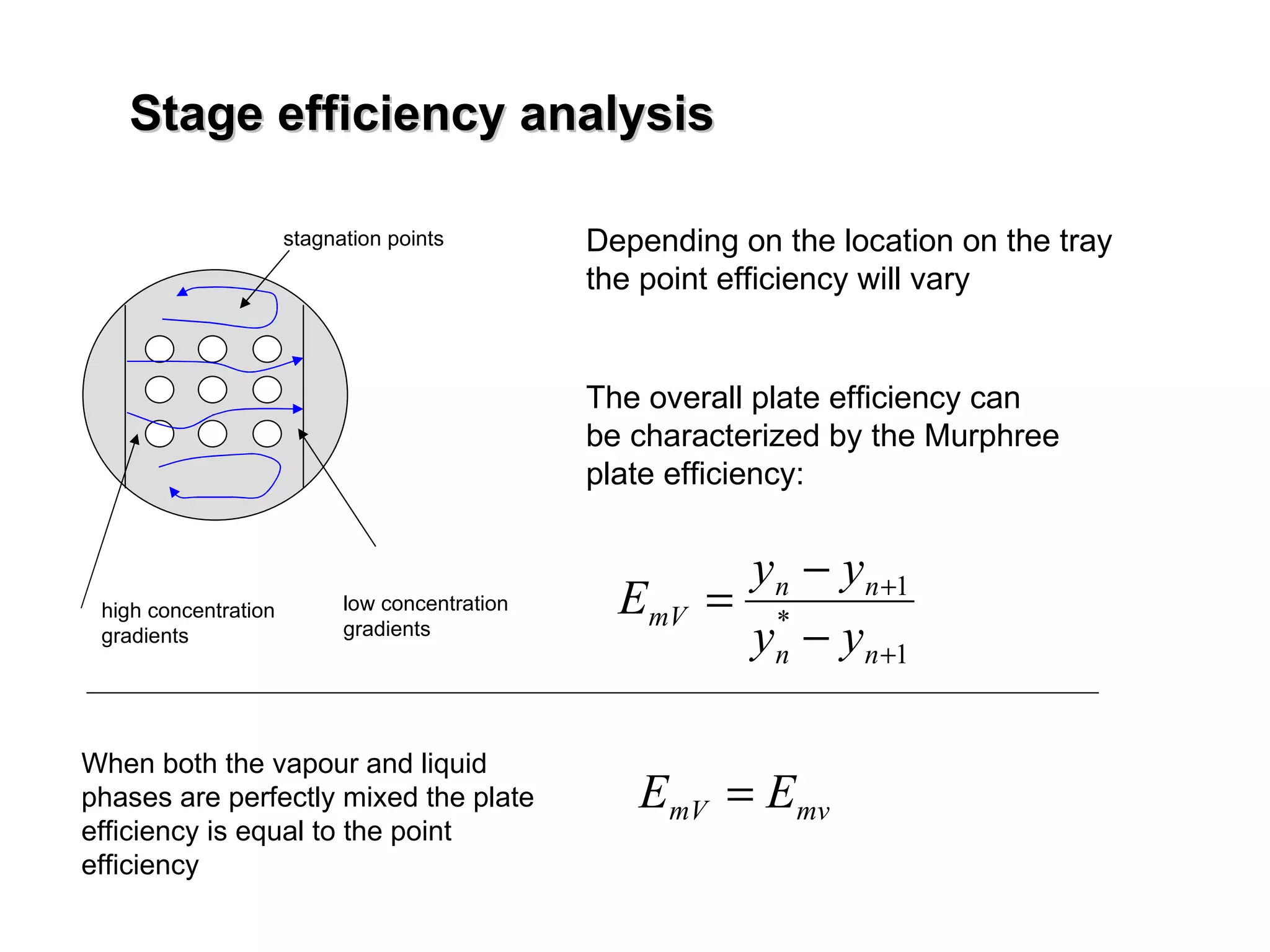
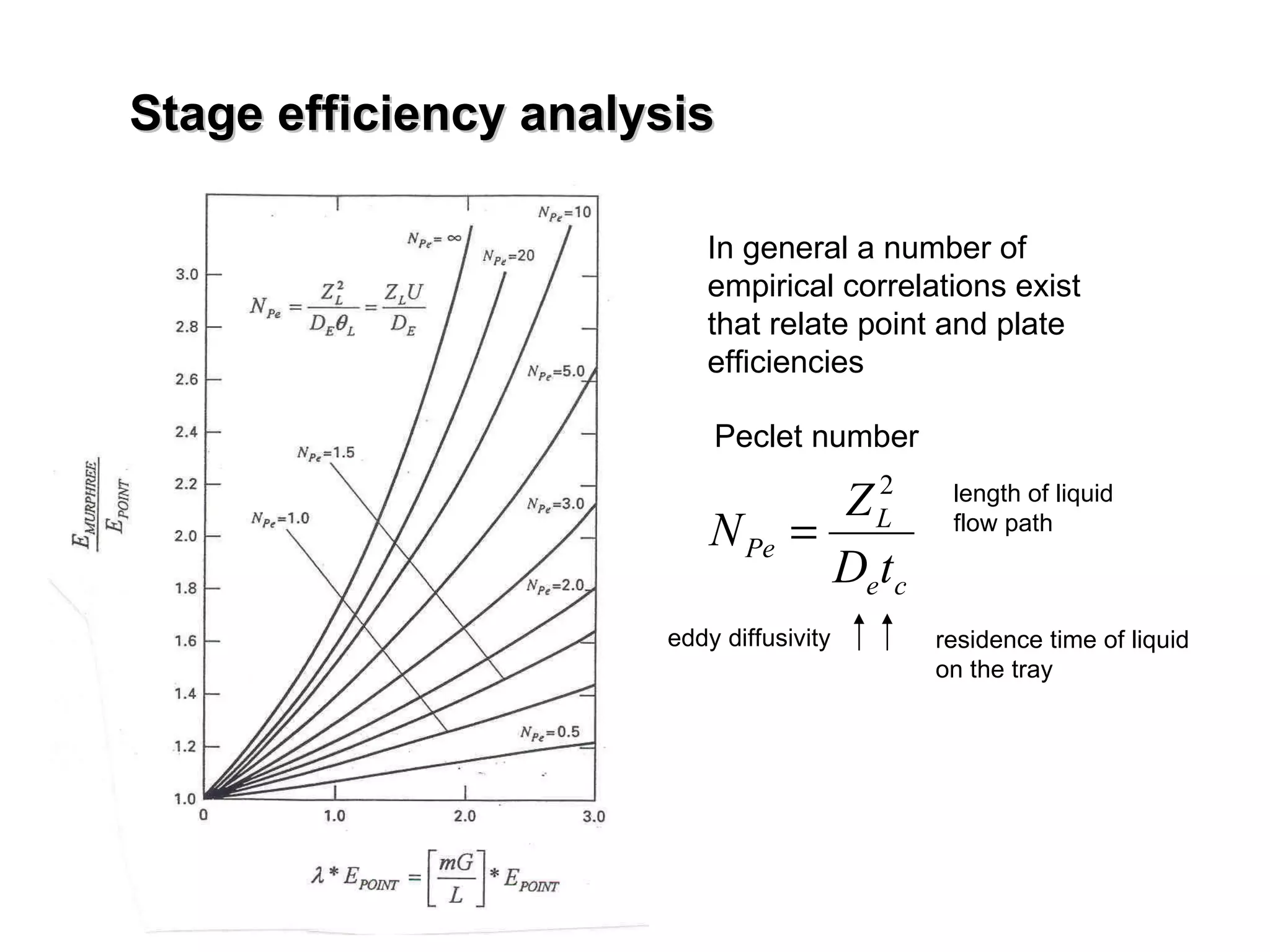
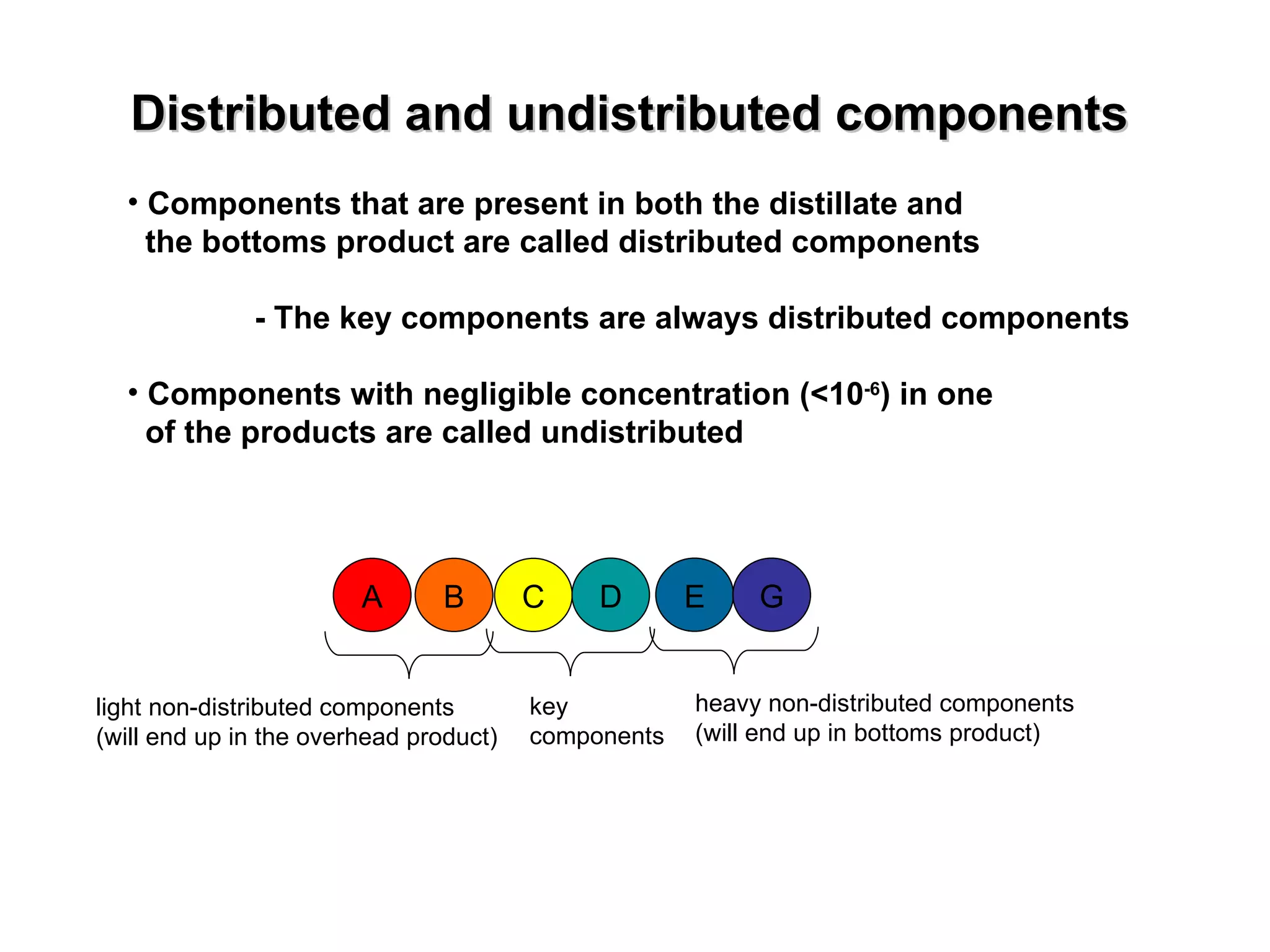
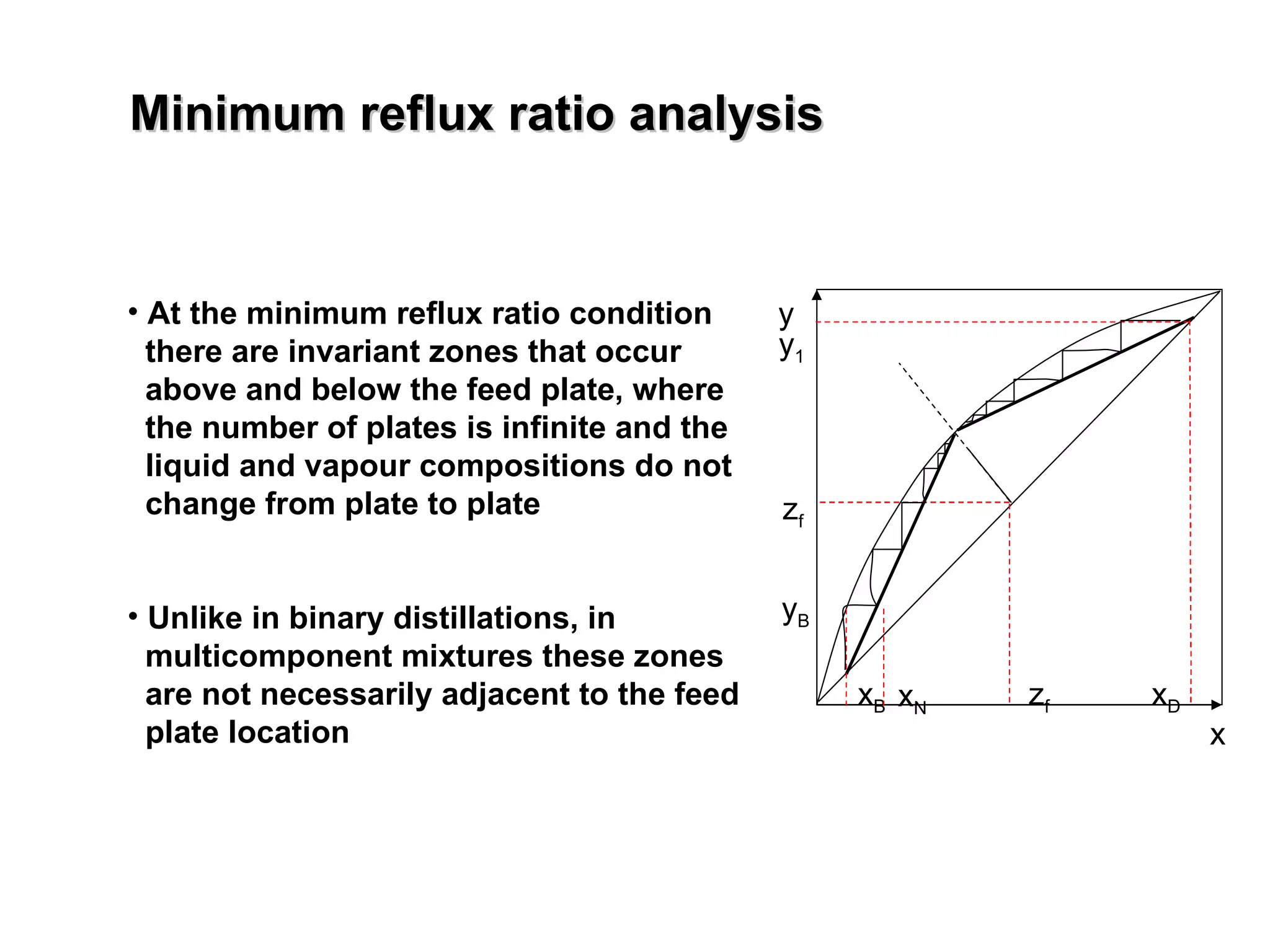
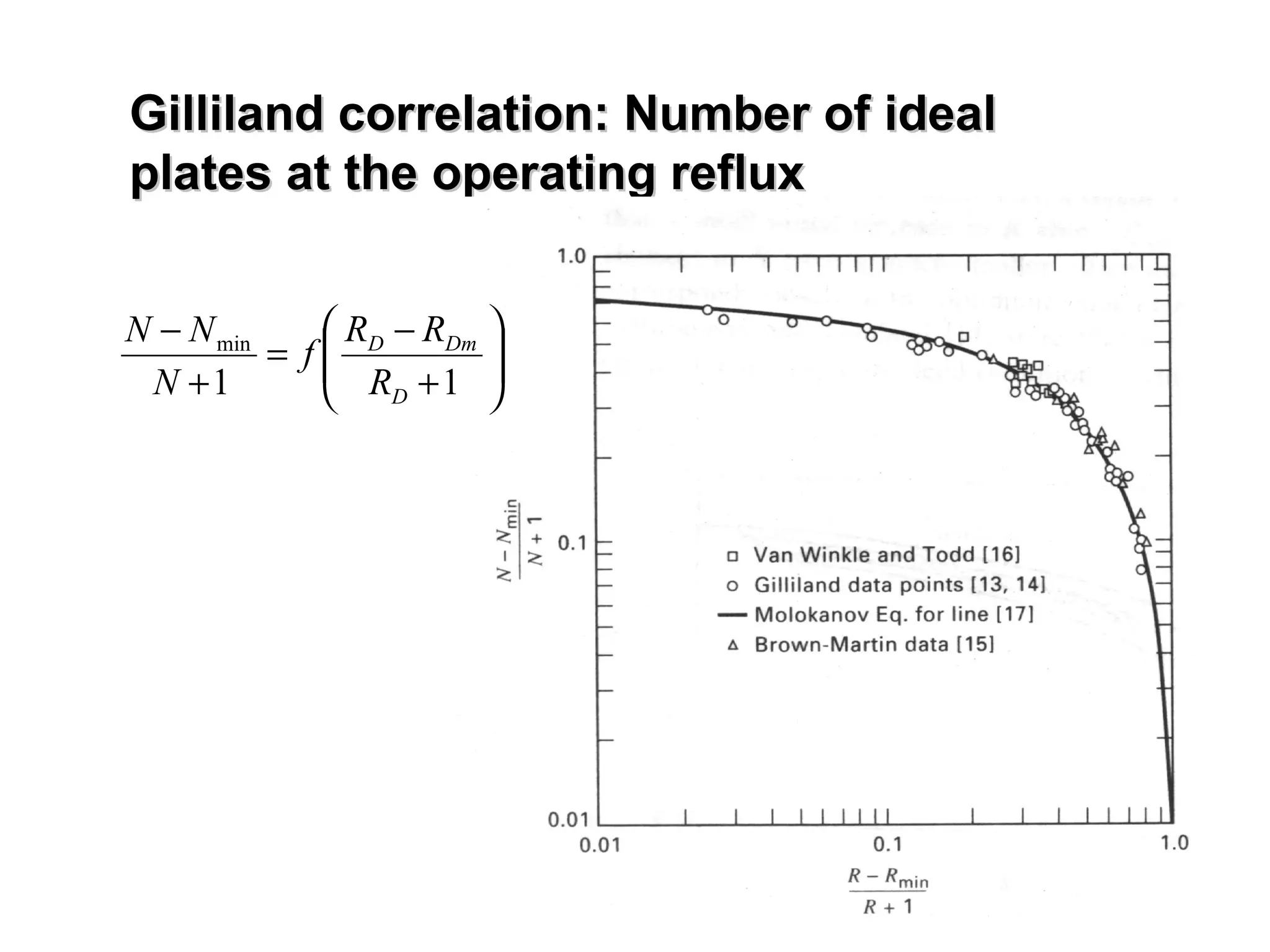
The document discusses key concepts in multicomponent distillation including: - Key components are chosen to indicate separation and are always distributed between products. - The Fenske equation is used to determine minimum number of stages assuming constant relative volatility, while the Underwood method determines minimum reflux ratio. - The Gilliland correlation estimates actual number of stages given operating reflux from minimum values.

1. Introduction to multicomponent distillation Most of the distillation processes deal with multicomponent mixtures Multicomponent phase behaviour is much more complex than that for the binary mixtures Rigorous design requires computers Short cut methods exist to outline the scope and limitations of a particular process

2. Multicomponent distillation in tray towers Objective of any distillation process is to recover pure products In case of multicomponent mixtures we may be interested in one, two or more components Unlike in binary distillation, fixing mole fraction of one of the components in a product does not fix the mole fraction of other components On the other hand fixing compositions of all the components in the distillate and the bottoms product, makes almost impossible to meet specifications exactly D B y 1 ,y 2 ,y 3 ,y 4 …

3. Key components In practice we usually choose two components separation of which serves as an good indication that a desired degree of separation is achieved These two components are called key components - light key - heavy key There are different strategies to select these key components Choosing two components that are next to each other on the relative volatility scale often leads to all the components lighter then the light key components accumulating in the distillate and all the components heavier then the heavy key component accumulating in the bottoms product: sharp separation

4. Distributed and undistributed components Components that are present in both the distillate and the bottoms product are called distributed components - The key components are always distributed components Components with negligible concentration (<10 -6 ) in one of the products are called undistributed A B C D E G key components heavy non-distributed components (will end up in bottoms product) light non-distributed components (will end up in the overhead product)

5. Fenske equation for multicomponent distillations Assumption : relative volatilities of components remain constant throughout the column LK – light component HK – heavy component

6. Fenske equation for multicomponent distillations Choices for relative volatility: D B T 1) Relative volatility at saturated feed condition 2) Geometric mean relative volatility why geometric mean?

7. Non key component distribution from the Fenske equation Convince yourself and derive for

8. Minimum reflux ratio analysis At the minimum reflux ratio condition there are invariant zones that occur above and below the feed plate, where the number of plates is infinite and the liquid and vapour compositions do not change from plate to plate Unlike in binary distillations, in multicomponent mixtures these zones are not necessarily adjacent to the feed plate location y x z f z f x B x D y 1 y B x N

9. * Relative volatility of each component has to be the same for each invariant zone * Constant molar overflow * α i =K i /K ref (Usually K ref =K HK ) The operating line equations for each section of the column become: Underwood method rectifying section stripping section Minimum reflux ratio analysis

10. rectifying section stripping section In the invariant zones: Underwood method Minimum reflux ratio analysis

11. We are looking for a condition where this is correct. In general there are multiple solutions But consider the following Underwood method Minimum reflux ratio analysis

12. In other words: Under Underwood conditions: A= Ā, Underwood method Minimum reflux ratio analysis

13. Minimum reflux ratio analysis: Underwood equations For a given q, and the feed composition we are looking for A satisfies this equation (usually A is between α LK and α HK . Once A is found, we can calculate the minimum reflux ratio

14. Gilliland correlation: Number of ideal plates at the operating reflux

15. Kirkbride equation: Feed stage location

16. Complete short cut design: Fenske-Underwood-Gilliland method Given a multicomponent distillation problem: a) Identify light and heavy key components b) Guess splits of the non-key components and compositions of the distillate and bottoms products c) Calculate d) Use Fenske equation to find Nmin e) Calculate distribution of non key components f) Use Underwood method to find R Dm g) Use Gilliland correlation to find actual number of ideal stages given operating reflux h) Use Kirkbride equation to locate the feed stage

17. Complete short cut design: example A mixture of 4% n-pentane, 40% n-hexane, 50% n-heptane and 6% n-octane is distilled at 1 atm. The goal is to recover 98%of hexane and 1% of heptane in the distillate. The feed is boiling liquid. a) Find minimum number of stages and minimum reflux ratio b) Given operating reflux of 1.5 of the minimum find the operating number of ideal stages 0.23 6 0.06 Octane 100 0.56 50 0.5 Heptane 1.39 40 0.4 Hexane 3.62 4 0.04 Pentane Ki x B Moles in B x D Moles in D F x F x F

18. Stage efficiency analysis Step 1: Thermodynamics data and methods to predict equilibrium phase compositions Step 2: Design of equilibrium stage separation Step 3: Develop an actual design by applying the stage efficiency analysis to equilibrium stage design

19. Stage efficiency analysis In general the overall efficiency will depend: 1) Geometry and design of contact stages 2) Flow rates and patterns on the tray 3) Composition and properties of vapour and liquid streams

20. Stage efficiency analysis Local efficiency Actual separation Separation that would have been achieved on an ideal tray What are the sources of inefficiencies? For this we need to look at what actually happens on the tray Point efficiency L in ,x in L out ,x out V out ,y out V in ,y in

21. Stage efficiency analysis Depending on the location on the tray the point efficiency will vary high concentration gradients low concentration gradients stagnation points The overall plate efficiency can be characterized by the Murphree plate efficiency: When both the vapour and liquid phases are perfectly mixed the plate efficiency is equal to the point efficiency

22. Stage efficiency analysis In general a number of empirical correlations exist that relate point and plate efficiencies Peclet number length of liquid flow path eddy diffusivity residence time of liquid on the tray

23. Stage efficiency analysis: O’Connell (1946)

24. Stage efficiency analysis: Van Winkle (1972)

25. Stage efficiency analysis - AICHE method - Fair-Chan Chan, H., J.R. Fair,” Prediction of Point Efficiencies for Sieve Trays, 1. Binary Systems”, Ind Eng. Chem. .Process Des. Dev., 23 , 814-819 (1984) Chan, H., J.R. Fair, ,” Prediction of Point Efficiencies for Sieve Trays, 1. Multi-component Systems”, Ind Eng. Chem. .Process Des. Dev., 23 , 820-827 (1984)

26. Stage efficiency analysis In addition we need to take in account effects of entrainment Entrained liquid droplets Dry Murphree efficiency can be corrected for the entrainment effects by Colburn equation: entrainment fraction = entrained liquid/gross liquid flow

27. Stage efficiency analysis

28. Stage efficiency analysis Finally the overall efficiency of the process defined as

29. Types of trays 1. Sieve plates 2. Bubble-cap plates 3. Valve plates

30. Types of trays