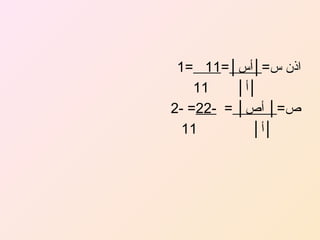يتناول الوثيقة مفهوم المحددات في الرياضيات، حيث يتم تعريف محدد مصفوفة معينة وكيفية حسابه، مع التركيز على المصوفات المربعة. كما توضح أمثلة متعددة لحساب محددات مختلف الرتب وتشرح طريقة كريمر لحل المعادلات الخطية باستخدام المحددات. الوثيقة تشمل أيضًا أمثلة على كيفية التعامل مع مصفوفات أكثر تعقيدًا وتطبيقات على محددات الرتبة الثالثة.