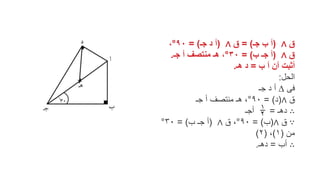
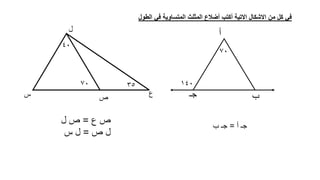
يتناول الوثيقة مفاهيم أساسية في الجبر، مثل العمليات على المجموعات والفترات العددية، بما في ذلك الاتحاد، والتقاطع، والفرق. كما يتضمن الواجبات المتعلقة بحساب الفترات، وتطبيقات الأعداد والعمليات، بالإضافة إلى مسائل هندسية وأرقام متفاوتة في مختلف السياقات. الوثيقة تقدم أيضًا طرقًا لحل المعادلات الرياضية وإنجاز بعض التمارين المتعلقة بالأشكال الهندسية.

1. ‫الجبر‬

2. ‫االس‬ ‫ويمكن‬ ‫المكملة‬ ‫و‬ ‫والفرق‬ ‫والتقاطع‬ ‫االتحاد‬ ‫هي‬ ‫الفترات‬ ‫على‬ ‫العمليات‬
‫تعانة‬
‫بالتمثيل‬
‫البيانى‬
‫العمليات‬ ‫تلك‬ ‫لتمثيل‬ ‫األعداد‬ ‫خط‬ ‫على‬ ‫للفترات‬
∩
‫بين‬ ‫المشتركة‬ ‫العناصر‬ ‫مجموعة‬
∪
‫الموجودة‬ ‫العناصر‬ ‫مجموعة‬
‫فى‬
،
‫تكرار‬ ‫دون‬
-
‫الموجودة‬ ‫العناصر‬ ‫مجموعة‬
‫فى‬
‫موجودة‬ ‫وغير‬
‫فى‬
-
‫الموجودة‬ ‫العناصر‬ ‫مجموعة‬
‫فى‬
‫موجودة‬ ‫وغير‬
‫فى‬
‫س‬
‫س‬
‫س‬
‫س‬
‫ص‬
‫س‬
‫س‬
‫س‬
‫س‬
‫ص‬
‫ص‬
‫ص‬
‫ص‬
‫ص‬
‫ص‬
‫ص‬

3. ‫كانت‬ ‫إذا‬
‫س‬
=
]
-
٣
،
٣
[
‫ص‬
=
]
-
١
،
٥
]
‫األعداد‬ ‫بخط‬ ‫ا‬ً‫ن‬‫مستعي‬ ‫اوجد‬
:
‫س‬
U
‫ص‬
-
١ ٥
-
٣ ٣
‫س‬
U
‫ص‬
=
]
-
٣
،
٥
]

4. ‫كانت‬ ‫إذا‬
‫س‬
=
]
-
٣
،
٣
[
‫ص‬
=
]
-
١
،
٥
]
‫األعداد‬ ‫بخط‬ ‫ا‬ً‫ن‬‫مستعي‬ ‫اوجد‬
:
‫س‬
∩
‫ص‬
-
١ ٥
-
٣ ٣
‫س‬
∩
‫ص‬
=
[ -
١
،
٣ ]

5. ‫كانت‬ ‫إذا‬
‫س‬
=
]
-
٣
،
٣
[
‫ص‬
=
]
-
١
،
٥
]
‫األعداد‬ ‫بخط‬ ‫ا‬ً‫ن‬‫مستعي‬ ‫اوجد‬
:
‫س‬
-
‫ص‬
-
١ ٥
-
٣ ٣
‫س‬
-
‫ص‬
=
] -
٣
،
-
١ ]

6. ‫كانت‬ ‫إذا‬
‫س‬
=
]
-
٣
،
٣
[
‫ص‬
=
]
-
١
،
٥
]
‫األعداد‬ ‫بخط‬ ‫ا‬ً‫ن‬‫مستعي‬ ‫اوجد‬
:
‫ص‬
-
‫س‬
-
١ ٥
-
٣ ٣
‫ص‬
-
‫س‬
=
] ٣
،
٥ [

7. ‫أكمل‬
:
1
-
٢٧
+
-
٦٤
=
2
-
٤
...... =
3
-
٢١٦
+
1
..........=
4
-
‫كان‬ ‫اذا‬
٢٥
=
‫س‬ ‫فان‬ ‫س‬
.....=
5
-
+ .......
٩
=
٢٥
6
-
‫حجمه‬ ‫الذي‬ ‫المكعب‬
٦٤
‫سم‬
٣
‫حرفه‬ ‫طول‬ ‫يكون‬
....... =
‫سم‬
3
3
3
3
3
3
‫ن‬
...... = U 7
-
‫ن‬
8
-
‫ح‬
+
∩
‫ح‬
-
=

8. ‫بين‬ ‫تنحصر‬ ‫نسبية‬ ‫غير‬ ‫أعداد‬ ‫أربعة‬ ‫أوجد‬
٤
,
٥
‫العددين‬ ‫بتربيع‬
(
٤
= )
١٦
‫و‬
(
٥
=)
٢٥
‫بين‬ ‫أعداد‬ ‫أربعة‬ ‫نختار‬
١٦
‫و‬
٢٥
١٧
‫و‬
١٨
‫و‬
١٩
‫و‬
٢٠
‫لألعداد‬ ‫التربيعي‬ ‫الجذر‬ ‫نأخذ‬ ‫ثم‬
١٧
١٨
١٩
٢٠

9. ‫نسب‬ ‫غير‬ ‫أيها‬ ‫و‬ ‫نسبي‬ ‫االتية‬ ‫االعداد‬ ‫من‬ ‫أي‬ ‫بين‬
‫ي‬
:
٠.٢٥
١.٢
٠.٩
٥
+

10. ‫مثال‬
:
‫النسبي‬ ‫غير‬ ‫للعدد‬ ‫تقريبية‬ ‫قيمة‬ ‫أوجد‬
‫العدد‬
٥
‫العددين‬ ‫بين‬ ‫ينحصر‬
٤
،
٩
(
‫كامل‬ ‫مربع‬ ‫منهما‬ ‫كل‬ ‫ألن‬ ‫للعددين‬ ‫اختيارنا‬ ‫وسبب‬
)
‫منهما‬ ‫كل‬ ‫نسبيين‬ ‫عددين‬ ‫نختار‬
‫العدد‬ ‫يحصران‬ ‫كامل‬ ‫مربع‬
٥
٩ > ٥ > ٤
‫التربي‬ ‫الجذر‬ ‫وبأخذ‬
‫عي‬
>
>
٣ > > ٢
‫أن‬ ‫أي‬
=
٢
+
‫الصحيح‬ ‫الواحد‬ ‫من‬ ‫أقل‬ ‫كسر‬

11. ‫بين‬ ‫ينحصر‬ ‫ان‬ ‫اثبت‬
1.7
،
1.8
‫الحل‬
(
1.7
= )
٢.٨٩
(
1.8
= )
٣.٢٤
= ) (
٣
‫الجذر‬ ‫بأخذ‬
‫بالتربيع‬
‫ترتيب‬
٣.٢٤ > ٣ > ٢.٨٩
١.٨ > > ١.٧

12. ‫يأتي‬ ‫مما‬ ‫كال‬ ‫اوجد‬
1
-
١٠٠٠
2
-
٠.٠٦٤
3
3

13. ‫األتية‬ ‫المعادالت‬ ‫من‬ ‫كل‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬
:
(
١
)
١٢٥
‫س‬
٣
-
٢٧
=
٠
١٢٥
‫س‬
٣
=
-
٢٧
‫س‬
٣
=
-
٢٧
١٢٥
‫س‬
٣
=
-
٢٧
١٢٥
3

14. (
٢
( )
‫س‬
٢
+
٢
)
(
‫س‬
٣
+
1
=)
0
‫اما‬
(
‫س‬
٢
+
٢
= )
٠
‫او‬
(
‫س‬
٣
+
١
=)
٠
‫س‬
٢
=
-
٢
‫س‬
=
-
٢
‫م‬
.
‫ح‬
=
Ø
‫س‬
٣
=
-
١
‫س‬
=
-
١
3
‫م‬
.
‫ح‬
=
}
-
١
{

15. ‫االعداد‬ ‫تنازليا‬ ‫رتب‬
٢
‫الجذور‬ ‫رتبة‬ ‫نفس‬ ‫لهم‬ ‫يكون‬ ‫ان‬ ‫يجب‬ ‫األعداد‬ ‫لترتيب‬
‫األعداد‬ ‫بترتيب‬
٢
=
=
٣
=
٢

16. ‫أكمل‬
:
= { ٣
،
٤ } U ] ٣
،
٤ ] 1
-
٣ ٤
= { ٣
،
٤ } - ] ٣
،
٤ ] 2
-
٣ ٤

17. ‫الهندسة‬

18. ‫أكمل‬
:
1
-
‫بنسبة‬ ‫المتوسط‬ ‫تقسم‬ ‫المثلث‬ ‫متوسطات‬ ‫تقاطع‬ ‫نقطة‬
.... : ....
‫الرأس‬ ‫جهة‬ ‫من‬
2
-
‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫متوسطات‬ ‫عدد‬
......
‫متوسط‬
3
-
‫الزاوية‬ ‫قائم‬ ‫المثلث‬ ‫في‬ ‫الوتر‬ ‫طول‬
.... =
‫للزاوية‬ ‫المقابل‬ ‫الضلع‬ ‫طول‬
٣٠
4
-
‫الزاوية‬ ‫القائم‬ ‫المثلث‬ ‫في‬ ‫القائمة‬ ‫الزاوية‬ ‫من‬ ‫الخارج‬ ‫المتوسط‬ ‫طول‬
... =
‫طول‬
‫الوتر‬

19. ‫أ‬
‫ب‬ ‫جـ‬
‫د‬
‫فى‬
‫المقابل‬ ‫الشكل‬
:
‫ق‬ ،‫ب‬ ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫أ‬
(
‫جـ‬
= )
٣٠
‫منتصف‬ ‫د‬
‫أجـ‬ ‫وكان‬ ،‫جـ‬ ‫أ‬
=
١٢
‫سم‬
.
‫د‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫أحسب‬
.
‫الحل‬
:
∵
‫أجـ‬ ‫منتصف‬ ‫د‬
∴
‫أد‬
=
٦
‫سم‬
∵
‫القائمة‬ ‫الرأس‬ ‫من‬ ‫خارج‬ ‫متوسط‬ ‫د‬ ‫ب‬
∵
‫د‬ ‫ب‬
‫أجـ‬ ‫طول‬ ‫نصف‬ ‫يساوي‬
∴
‫د‬ ‫ب‬
=
٦
‫سم‬
∴
‫للزاوية‬ ‫مقابل‬ ‫ضلع‬ ‫ب‬ ‫أ‬
٣٠
‫أب‬
=
‫جـ‬ ‫أ‬
‫ب‬ ‫أ‬
=
٦
‫سم‬
‫المحيط‬
=
٦
+
٦
+
٦
=
١٨
‫سم‬

20. ‫أ‬
‫ب‬ ‫جـ‬
‫د‬
‫هـ‬
‫فى‬
‫المقابل‬ ‫الشكل‬
:
‫ق‬ ،‫ب‬ ‫في‬ ‫الزاوية‬ ‫قائم‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫أ‬
(
‫هـ‬
= )
٣٠
‫ق‬
(
‫هـ‬ ‫د‬ ‫ب‬
= )
٩٠
‫منتصف‬ ‫د‬
،‫جـ‬ ‫أ‬
‫أجـ‬ ‫ان‬ ‫أثبت‬
=
‫هـ‬ ‫ب‬
.
‫الحل‬
:
∵
‫أجـ‬ ‫منتصف‬ ‫د‬
∵
‫القائمة‬ ‫الرأس‬ ‫من‬ ‫خارج‬ ‫متوسط‬ ‫د‬ ‫ب‬
∵
‫د‬ ‫ب‬
=
‫أجـ‬
∴
‫للزاوية‬ ‫مقابل‬ ‫ضلع‬ ‫د‬ ‫ب‬
٣٠
‫د‬ ‫ب‬
=
‫جـ‬ ‫أ‬
‫أجـ‬
=
‫د‬ ‫ب‬

21. ‫ق‬
∧
(
‫جـ‬ ‫ب‬ ‫أ‬
)
=
‫ق‬
∧
(
‫جـ‬ ‫د‬ ‫أ‬
)
=
٩٠
°
،
‫ق‬
∧
(
‫ب‬ ‫جـ‬ ‫أ‬
)
=
٣٠
°
‫منتصف‬ ‫هـ‬ ،
‫جـ‬ ‫أ‬
.
‫ب‬ ‫أ‬ ‫أن‬ ‫أثبت‬
=
‫هـ‬ ‫د‬
.
‫الحل‬
:
‫فى‬
∆
‫جـ‬ ‫د‬ ‫أ‬
‫ق‬
∧
(
‫د‬
)
=
٩٠
°
‫منتصف‬ ‫هـ‬ ،
‫جـ‬ ‫أ‬
∴
‫دهـ‬
=
‫أجـ‬
∵
‫ق‬
∧
(
‫ب‬
)
=
٩٠
°
،
‫ق‬
∧
(
‫ب‬ ‫جـ‬ ‫أ‬
)
=
٣٠
°
‫من‬
(
١
)
،
(
٢
)
∴
‫أب‬
=
‫دهـ‬
.

22. ‫الضلعين‬ ‫متطابق‬ ‫د‬ ‫ع‬ ‫س‬
.
‫الرأس‬ ‫زاوية‬ ‫قياس‬
‫س‬
=
٦٠
.
‫أن‬ ‫أثبت‬
‫ق‬
(
‫ع‬
)
=
‫ق‬
(
‫د‬
)
=
٦٠
‫الحل‬
:
‫زوايا‬ ‫قياسات‬ ‫مجموع‬ ‫ألن‬
‫ه‬
=
١٨٠
‫الضلعين‬ ‫متطابق‬ ‫المثلث‬ ‫ألن‬
.

23. ‫أ‬
‫جـ‬ ‫ب‬
‫أ‬
‫ب‬
‫جـ‬
‫أ‬
‫ب‬
‫جـ‬
‫د‬
‫س‬
٧٠
‫س‬
‫ص‬
٧٤ ٨٠
‫س‬
‫الزاوي‬ ‫قياس‬ ‫في‬ ‫المستخدم‬ ‫الرمز‬ ‫قيمة‬ ‫أوجد‬ ‫االتية‬ ‫االشكال‬ ‫من‬ ‫كل‬ ‫في‬
‫ة‬
‫س‬
=
٥٥
‫س‬
=
٤٥
‫ص‬
=
٤٥
‫س‬
=
٥٠
+
٧٤
=
١٢٤

24. ‫المعطيات‬
:
‫أب‬ ‫فيه‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫أ‬
=
‫جـ‬ ‫ب‬ ‫دن‬ ، ‫جـ‬ ‫أ‬
‫المطلوب‬
:
‫الساقين‬ ‫متساوي‬ ‫ن‬ ‫د‬ ‫أ‬ ‫المثلث‬ ‫أن‬ ‫اثبات‬
‫البرهان‬
:
‫أب‬
=
‫أجـ‬
‫ق‬
(
‫جـ‬ ‫أب‬
= )
‫ق‬
(
‫ب‬ ‫جـ‬ ‫أ‬
( )
1
)
‫لهما‬ ‫قاطع‬ ‫ب‬ ‫أ‬ ‫جـ‬ ‫ب‬ ‫دن‬
‫ق‬
(
‫جـ‬ ‫أب‬
= )
‫ق‬
(
‫ن‬ ‫د‬ ‫أ‬
)
‫بالتناظر‬
(
2
)
‫لهما‬ ‫قاطع‬ ‫ب‬ ‫أ‬ ‫جـ‬ ‫ب‬ ‫دن‬
‫ق‬
(
‫ب‬ ‫أجـ‬
= )
‫ق‬
(
‫د‬ ‫ن‬ ‫أ‬
)
‫بالتناظر‬
(
3
)
‫من‬
(
1
)
،
(
2
)
،
(
3
)
‫ان‬ ‫ينتج‬
:
‫ق‬
(
‫ن‬ ‫د‬ ‫أ‬
= )
‫ق‬
(
‫د‬ ‫ن‬ ‫أ‬
)
‫أد‬
=
‫أن‬
‫الساقين‬ ‫متساوي‬ ‫ن‬ ‫د‬ ‫أ‬ ‫المثلث‬
‫أ‬
‫ب‬
‫د‬
‫جـ‬
‫أب‬ ‫المقابل‬ ‫الشكل‬ ‫في‬
=
‫الساقين‬ ‫متساوي‬ ‫ن‬ ‫د‬ ‫أ‬ ‫المثلث‬ ‫ان‬ ‫أثبت‬ ‫جـ‬ ‫ب‬ ‫ن‬ ‫د‬ ، ‫أجـ‬
‫ن‬

25. ٧٠
١٤٠
٣٥
‫ل‬
‫ع‬
‫س‬
‫ع‬ ‫ص‬
=
‫ل‬ ‫ص‬
‫ص‬ ‫ل‬
=
‫س‬ ‫ل‬
‫أ‬
‫جـ‬ ‫ب‬
‫ص‬
‫أ‬ ‫جـ‬
=
‫ب‬ ‫جـ‬
٧٠
٤٠
‫الطول‬ ‫في‬ ‫المتساوية‬ ‫المثلث‬ ‫أضالع‬ ‫أكتب‬ ‫االتية‬ ‫االشكال‬ ‫من‬ ‫كل‬ ‫في‬