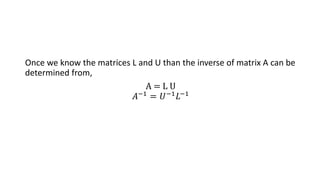This document describes the triangularization method for solving systems of linear equations. It involves decomposing the coefficient matrix A into the product of a lower triangular matrix L and an upper triangular matrix U. This decomposition is done by calculating the elements of L and U such that their product equals the original matrix A. The system of linear equations can then be solved through back substitution by first solving the system LUx=B as two separate systems involving L and U. The triangularization method is preferable to Gaussian elimination as it requires fewer operations and can also be used to find the inverse of a matrix. However, it fails if any diagonal elements of L or U are zero.

1. Triangularization Method
- Kamran Ansari
6th Semester

2. Contents
• Introduction
• Formula and method
• Limitations of Triangularizatoin method
• Advantages of Triangularization Method

3. Introduction
• Triangularization Method is also known as decomposition method or
the factorization method.
• It is a type of direct method of solving linear simultaneous equations.
• It is also useful for determining the inverse of matrix.

4. Formula and method
Consider the linear equations,
𝑎11 𝑥 + 𝑎12 𝑦 + 𝑎13 𝑧 = 𝑏1
𝑎21 𝑥 + 𝑎22 𝑦 + 𝑎23 𝑧 = 𝑏2
𝑎31 𝑥 + 𝑎32 𝑦 + 𝑎33 𝑧 = 𝑏3
can be written as AX = B ……(1)
𝐴 =
𝑎11 𝑎12 𝑎13
𝑎21 𝑎22 𝑎23
𝑎31 𝑎32 𝑎33
𝑋 =
𝑥
𝑦
𝑧
and B =
𝑏1
𝑏2
𝑏3

5. The concept behind this method is that any matrix A can be expressed
as the product of a lower triangular matrix L and an upper triangular
matrix U provided all the principal minors of A is non singular.
A = L U
To produce a unique solution, it is convenient to choose either,
1. 𝑙𝑖𝑖 = 1, the method is called the Doolittle’s method, or
2. 𝑢𝑖𝑖 = 1, the method is called the Crout’s method.

6. By using Doolittle’s method, A = L U ……(2)
where 𝐿 =
1 0 0
𝑙21 1 0
𝑙31 𝑙32 1
and 𝑈 =
𝑢11 𝑢12 𝑢13
0 𝑢22 𝑢23
0 0 𝑢33
We can calculate the elements of matrices L and U to use the equality of
matrices.
By equation (1) becomes, L U X = B
write as the following two systems of equations,
U X = V ……(3)
L V = B ……(4)
using equation (4), by substitution we can calculate the matrix V,
and at last by back substitution, matrix X can be obtained.

7. Once we know the matrices L and U than the inverse of matrix A can be
determined from,
A = L U
𝐴−1
= 𝑈−1
𝐿−1

8. Limitations of Triangularizatoin Method
• This method fails if any of the diagonal elements of matrices
L and U (e.g. 𝑙𝑖𝑖 or 𝑢𝑖𝑖) is zero.
• All the principal minors of A is non singular.

9. Advantages of Triangularization Method
• This method is superior to Gauss elimination method and used for the
solution of linear systems and finding the inverse of the matrix.
• The number of operations involved in terms of multiplication for a
system of linear equations by triangularization method is less than
Gauss method.
• Among the direct methods, factorization method is also preferred as
the software for computers.

10. Thank you