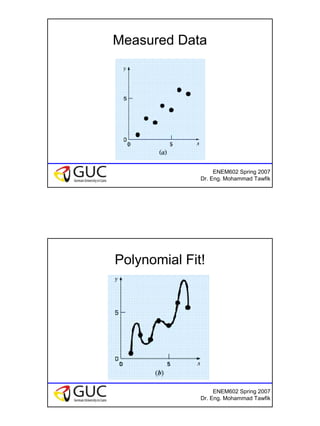
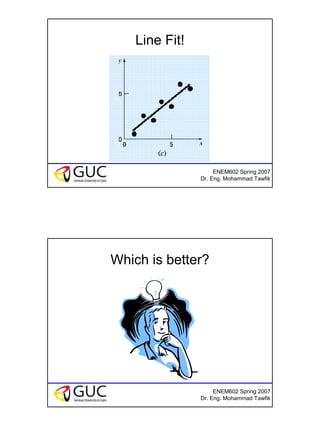
The document discusses curve fitting and regression analysis techniques. It explains the difference between interpolation and regression, and how polynomials and lines can be fitted to a set of data points. The objectives are to understand interpolation vs regression, how to fit polynomials to data, and how to use polynomials for interpolation. Examples are provided on finding the best fit line and parabola to given data sets. The key steps of determining constants that minimize the error in the fit are shown.




![8
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
For every point
nn xaay
xaay
xaay
10
2102
1101
+≠
+≠
+≠
M
≠
1
02
1
2
1
1
1
1
a
a
x
x
x
y
y
y
nn
MMM
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
So, we may write the error vector
−
=
1
02
1
2
1
2
1
1
1
1
a
a
x
x
x
y
y
y
e
e
e
nnn
MMMM
{ } { } [ ] { } 1*22*1*1* aAye nnn −=](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-8-320.jpg)
![9
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Square the error
{ } { } [ ]{ }aAye −=
{ } { } { } { } { } [ ]{ }
{ } [ ] { } { } [ ] [ ]{ } 2
eaAAayAa
aAyyyee
TTTT
TTT
=+−
−=
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Note: this is a scalar equation!
{ } { } { } { } { } [ ]{ }
{ } [ ] { } { } [ ] [ ]{ } 2
eaAAayAa
aAyyyee
TTTT
TTT
=+−
−=
{ } [ ]{ } { } [ ] { }yAaaAy
TTT
=
{ } { } { } [ ] { } { } [ ] [ ]{ }aAAayAayye
TTTTT
+−= 2
2](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-9-320.jpg)
![10
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Note: this is a quadratic equation in {a}!!!
{ } { } { } [ ] { } { } [ ] [ ]{ }aAAayAayye
TTTTT
+−= 2
2
To minimize the error in the above equation, we need to
differentiate with respect to the parameters
{ }
[ ] { } [ ] [ ]{ } 022
2
=+−= aAAyA
ad
ed TT
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solving the equation
We get:
{ }
[ ] { } [ ] [ ]{ } 022
2
=+−= aAAyA
ad
ed TT
[ ] [ ] { } [ ] { } 1**21*22**2 n
T
nn
T
n yAaAA =
[ ] { } { } 1*21*22*2 yaA = { } [ ] { }yAa
1−
=](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-10-320.jpg)
![11
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example
• If you are given the
data.
• Find the equation of
the “best-fit” line.
y=a1+a2x
5.57
66
3.55
44
23
2.52
0.51
yx
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
=
5.5
6
5.3
4
2
5.2
5.0
71
61
51
41
31
21
11
1
0
a
a
[ ] { }
=
=
5.5
6
5.3
4
2
5.2
5.0
&
71
61
51
41
31
21
11
yA](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-11-320.jpg)
![12
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
[ ] [ ]
=
=
14028
287
71
61
51
41
31
21
11
7654321
1111111
AA
T
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
[ ] { }
=
=
5.119
24
5.5
6
5.3
4
2
5.2
5.0
7654321
1111111
yA
T](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-12-320.jpg)
![13
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
=
5.119
24
14028
287
1
0
a
a
[ ] [ ]{ } [ ] { }yAaAA
TT
=
=
8393.0
0714.0
1
0
a
a
0714.08393.0 += xy
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Example
• If you are given the
data.
• Find the equation of
the “best-fit” parabola.
y=a0+a1x+a2x2
5.57
66
3.55
44
23
2.52
0.51
yx](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-13-320.jpg)
![14
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
=
5.5
6
5.3
4
2
5.2
5.0
49
36
25
16
9
4
1
71
61
51
41
31
21
11
2
1
0
a
a
a
[ ] { }
=
=
5.5
6
5.3
4
2
5.2
5.0
&
49
36
25
16
9
4
1
71
61
51
41
31
21
11
yA
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
[ ] [ ]
=
=
4676784140
78414028
140287
49
36
25
16
9
4
1
71
61
51
41
31
21
11
49362516941
7654321
1111111
AA
T](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-14-320.jpg)
![15
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
[ ] { }
=
=
5.665
5.119
24
5.5
6
5.3
4
2
5.2
5.0
49362516941
7654321
1111111
yA
T
ENEM602 Spring 2007
Dr. Eng. Mohammad Tawfik
Solution
[ ] [ ]{ } [ ] { }yAaAA
TT
=
−
−
=
0298.0
0774.1
2857.0
2
1
0
a
a
a
2857.00774.10298.0 2
−+−= xxy](https://image.slidesharecdn.com/06regression-101108031229-phpapp01/85/06-regression-15-320.jpg)
