Download to read offline
Uploaded byMohammad Tawfik
04 gaussmethods
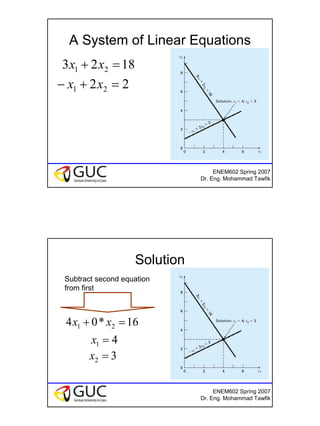
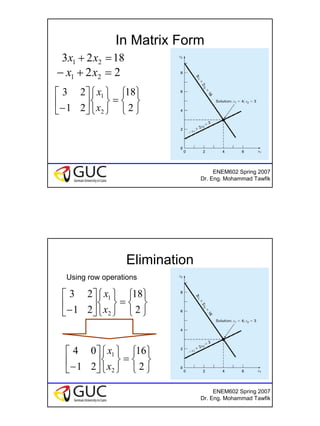
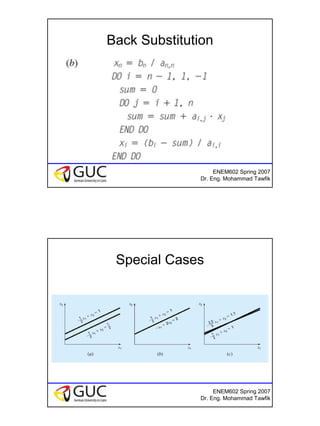
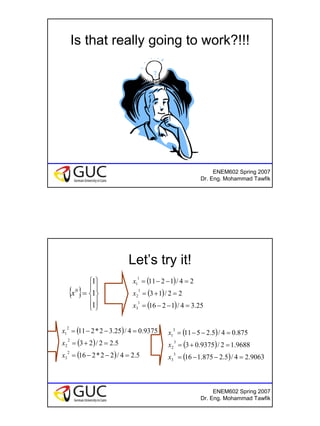
This document discusses iterative methods for solving systems of linear equations. It introduces the Gauss-Jacobi and Gauss-Seidel methods. For Gauss-Jacobi, each new approximation is calculated from the previous approximations. For Gauss-Seidel, the most recent approximation is used. The document provides examples of applying each method and discusses conditions for convergence. As homework, students are asked to use the two methods to approximate solutions for a given system of equations.
More Related Content
04 gaussmethods
- 1. 1 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Linear Algebraic Equations Gauss Elimination ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Objectives • Knowing how to solve a system of linear equations • Understanding how to implement Gauss elimination method • Understanding the concepts of singularity and ill-conditioning
- 2. 2 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik A System of Linear Equations 1823 21 =+ xx 22 21 =+− xx ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Solution Subtract second equation from first 16*04 21 =+ xx 41 =x 32 =x
- 3. 3 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik In Matrix Form = − 2 18 21 23 2 1 x x 1823 21 =+ xx 22 21 =+− xx ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Elimination = − 2 18 21 23 2 1 x x Using row operations = − 2 16 21 04 2 1 x x
- 4. 4 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Elimination Using row operations = − 2 16 21 04 2 1 x x = 6 16 20 04 2 1 x x ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Naïve Elimination Routine!
- 5. 5 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Back Substitution ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Special Cases
- 6. 6 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Conclusions • In this lecture, we revised the process of Gauss elimination • A clear algorithm for the elimination process and the back substitution was presented • The different cases of no solution, infinite number of solutions, and ill conditioning were graphically presented ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Linear Algebraic Equations Iterative Solutions
- 7. 7 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Objectives • Recognize the need for iterative solutions • Understand the difference between different iterative methods for solving systems of linear equations • Apply iterative methods to solve a system of linear equations ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Why Iterative Methods? • When system of equations is sparse; too many zero elements. Such systems are produced when approximately solving differential equations; finite difference, finite element, etc… • We already have sources of error in the solution; model errors, approximation errors, truncation errors, etc…, so why not use approximate method any way • Saves on time!
- 8. 8 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Gauss-Jacobi ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Gauss-Jacobi: Example 1642 302 1124 321 21 321 =++ =++− =++ xxx xx xxx ( ) ( ) ( ) 4/216 2/3 4/211 213 12 321 xxx xx xxx −−= += −−= ( ) ( ) ( ) 4/216 2/3 4/211 21 1 3 1 1 2 32 1 1 kkk kk kkk xxx xx xxx −−= += −−= + + +
- 9. 9 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Is that really going to work?!!! ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Let’s try it! { } = 1 1 1 0 x ( ) ( ) ( ) 25.34/1216 22/13 24/1211 1 3 1 2 1 1 =−−= =+= =−−= x x x ( ) ( ) ( ) 5.24/22*216 5.22/23 9375.04/25.32*211 2 3 2 2 2 1 =−−= =+= =−−= x x x ( ) ( ) ( ) 9063.24/5.2875.116 9688.12/9375.03 875.04/5.2511 3 3 3 2 3 1 =−−= =+= =−−= x x x
- 10. 10 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik In General! ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik A system of linear equations = nnnnnn n n b b b x x x aaa aaa aaa MM L MOMM L L 2 1 2 1 21 22221 11211 Let’s examine one equation! 11212111 ... bxaxaxa nn =+++ ( ) 11 12121 1 ... a xaxab x nn++− =
- 11. 11 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik For any equation −−= ∑∑ += − = + n ij k jij i j k jiji ii k i xaxab a x 1 1 1 1 1 ( ) ii niniiiiiiii i a xaxaxaxab x +++++− = ++−− ...... 11,11,11 ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Can it be any better?
- 12. 12 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Gauss-Seidel −−= ∑∑ += − = + n ij k jij i j k jiji ii k i xaxab a x 1 1 1 1 1 −−= ∑∑ += − = ++ n ij k jij i j k jiji ii k i xaxab a x 1 1 1 11 1 ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Gauss-Seidel: Example 1642 302 1124 321 21 321 =++ =++− =++ xxx xx xxx ( ) ( ) ( ) 4/216 2/3 4/211 213 12 321 xxx xx xxx −−= += −−= ( ) ( ) ( ) 4/216 2/3 4/211 1 2 1 1 1 3 1 1 1 2 32 1 1 +++ ++ + −−= += −−= kkk kk kkk xxx xx xxx
- 13. 13 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Let’s try it! { } = 1 1 1 0 x ( ) ( ) ( ) 375.24/5.22*216 5.22/23 24/1211 1 3 1 2 1 1 =−−= =+= =−−= x x x ( ) ( ) ( ) 0586.34/9531.1906.0*216 9531.12/90625.03 90625.04/375.2511 2 3 2 2 2 1 =−−= =+= =−−= x x x ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Convergence Condition • For the iterative solutions presented to converge, the matrix must be diagonally dominant. ∑ ≠ = > n ij j ijii aa 1
- 14. 14 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Error! { } { } { }kkk xxe −= −1 k i k ik a x e max=ε ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Algorithm 1. If the system is not diagonally dominant; end 2. Start with any initial solution {x} 3. Apply the steps for Gauss-Seidal method to evaluate the next iteration 4. If the maximum approximate relative error < εs; end 5. Let the old solution vector equal the new solution vector 6. Goto step 3
- 15. 15 ENEM602 Spring 2007 Dr.Eng. Mohammad Tawfik Homework #3 • For the given system of simultaneous equations • Write down the system of equation in a form that can be used for iterative methods for solving systems of equations • Use four iterations using Gauss-Jacobi method to find an approximate solution using initial values {0,0,0} • Use four iterations using Gauss-Seidel method to find an approximate solution using initial values {0,0,0} 1642 1124 32 321 321 21 =++ =++ =+− xxx xxx xx ENEM602 Spring 2007 Dr. Eng. Mohammad Tawfik Homework #3 cont’d • Chapter 11, p 303, numbers: 11.8,11.9,11.10 • Due Next week