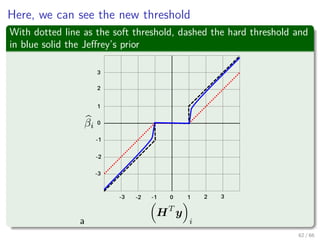
This document discusses Maximum A Posteriori (MAP) estimation for machine learning and data mining. It begins by introducing the Bayesian rule and defining the MAP as the value of Θ that maximizes the posterior p(Θ|X). It then shows how to develop the MAP solution by taking the logarithm of the posterior and finding the value of Θ that maximizes it. The MAP allows prior beliefs about parameter values to be incorporated into the estimation. An example application to binary classification with a Bernoulli model is provided. It derives the maximum likelihood solution and then extends it to the MAP by specifying a Beta prior distribution over the parameter.

























![Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0,1] interval.
Within the [0,1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
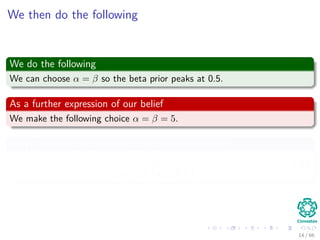
We assume the following
The state of Colima has traditionally voted PRI in presidential elections.
However, on account of the prevailing economic conditions, the voters are
more likely to vote PAN in the election in question.
12 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-27-320.jpg)
![Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0,1] interval.
Within the [0,1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential elections.
However, on account of the prevailing economic conditions, the voters are
more likely to vote PAN in the election in question.
12 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-28-320.jpg)
![Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0,1] interval.
Within the [0,1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential elections.
However, on account of the prevailing economic conditions, the voters are
more likely to vote PAN in the election in question.
12 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-29-320.jpg)
![Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0,1] interval.
Within the [0,1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential elections.
However, on account of the prevailing economic conditions, the voters are
more likely to vote PAN in the election in question.
12 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-30-320.jpg)
![Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0,1] interval.
Within the [0,1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential elections.
However, on account of the prevailing economic conditions, the voters are
more likely to vote PAN in the election in question.
12 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-31-320.jpg)






![Now, our MAP estimate for p...
We have then
pMAP = argmax
Θ
xi∈X
log p (xi|q) + log p (q)
(11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI ) log (1 − q) + log p (q)] (12)
Where
log P (p) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
16 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-40-320.jpg)
![Now, our MAP estimate for p...
We have then
pMAP = argmax
Θ
xi∈X
log p (xi|q) + log p (q)
(11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI ) log (1 − q) + log p (q)] (12)
Where
log P (p) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
16 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-41-320.jpg)
![Now, our MAP estimate for p...
We have then
pMAP = argmax
Θ
xi∈X
log p (xi|q) + log p (q)
(11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI ) log (1 − q) + log p (q)] (12)
Where
log P (p) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
16 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-42-320.jpg)
















![Introduction: Linear Regression with Gaussian Prior
We consider regression functions that are linear with respect to the
parameter vector β
f (x, β) =
k
i=1
βih (x) = βT
h (x)
Where
h (x) = [h1 (x) , ..., hk (x)]T
is a vector of k fixed function of the input,
often called features.
26 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-60-320.jpg)
![Introduction: Linear Regression with Gaussian Prior
We consider regression functions that are linear with respect to the
parameter vector β
f (x, β) =
k
i=1
βih (x) = βT
h (x)
Where
h (x) = [h1 (x) , ..., hk (x)]T
is a vector of k fixed function of the input,
often called features.
26 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-61-320.jpg)
![Actually, it can be...
Linear Regression
Linear regression, in which h (x) = [1, x1, ..., xd]T
i; in this case, k = d + 1.
Non-Linear Regression
Here, you have a fixed basis function where
h (x) = [φ1 (x) , φ2 (x) , ..., φ1 (x)]T
with φ1 (x) = 1.
Kernel Regression
Here h (x) = [1, K (x, x1) , K (x, x2) , ..., K (x, xn)]T
where K (x, xi) is
some kernel function.
27 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-62-320.jpg)
![Actually, it can be...
Linear Regression
Linear regression, in which h (x) = [1, x1, ..., xd]T
i; in this case, k = d + 1.
Non-Linear Regression
Here, you have a fixed basis function where
h (x) = [φ1 (x) , φ2 (x) , ..., φ1 (x)]T
with φ1 (x) = 1.
Kernel Regression
Here h (x) = [1, K (x, x1) , K (x, x2) , ..., K (x, xn)]T
where K (x, xi) is
some kernel function.
27 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-63-320.jpg)
![Actually, it can be...
Linear Regression
Linear regression, in which h (x) = [1, x1, ..., xd]T
i; in this case, k = d + 1.
Non-Linear Regression
Here, you have a fixed basis function where
h (x) = [φ1 (x) , φ2 (x) , ..., φ1 (x)]T
with φ1 (x) = 1.
Kernel Regression
Here h (x) = [1, K (x, x1) , K (x, x2) , ..., K (x, xn)]T
where K (x, xi) is
some kernel function.
27 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-64-320.jpg)

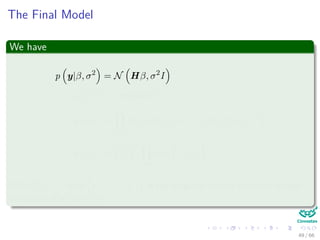
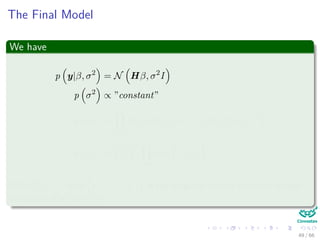
![Gaussian Noise
We assume that the training set is contaminated by additive white
Gaussian Noise
yi = f (xi, β) + ωi (17)
for i = 1, ..., N where [ω1, ..., ωN ] is a set of independent zero-mean
Gaussian samples with variance σ2
Thus, for [y1, ..., yN ], we have the following likelihood
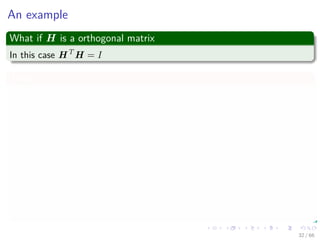
p (y|β) = N Hβ, σ2
I (18)
The posterior p (β|y) is still Gaussian and the mode is given by
β = σ2
I + HT
H
−1
HT
y (19)
Remark: The Ridge regression.
29 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-66-320.jpg)
![Gaussian Noise
We assume that the training set is contaminated by additive white
Gaussian Noise
yi = f (xi, β) + ωi (17)
for i = 1, ..., N where [ω1, ..., ωN ] is a set of independent zero-mean
Gaussian samples with variance σ2
Thus, for [y1, ..., yN ], we have the following likelihood
p (y|β) = N Hβ, σ2
I (18)
The posterior p (β|y) is still Gaussian and the mode is given by
β = σ2
I + HT
H
−1
HT
y (19)
Remark: The Ridge regression.
29 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-67-320.jpg)
![Gaussian Noise
We assume that the training set is contaminated by additive white
Gaussian Noise
yi = f (xi, β) + ωi (17)
for i = 1, ..., N where [ω1, ..., ωN ] is a set of independent zero-mean
Gaussian samples with variance σ2
Thus, for [y1, ..., yN ], we have the following likelihood
p (y|β) = N Hβ, σ2
I (18)
The posterior p (β|y) is still Gaussian and the mode is given by
β = σ2
I + HT
H
−1
HT
y (19)
Remark: The Ridge regression.
29 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-68-320.jpg)


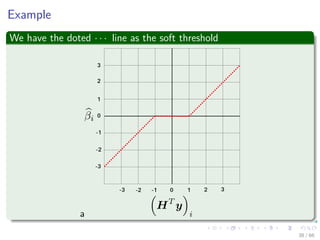
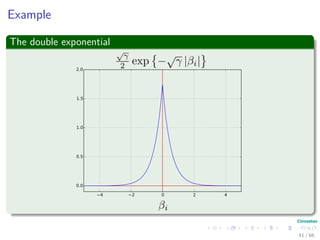
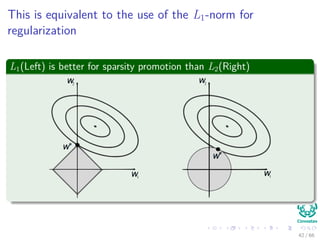
![Remark
This criterion is know as the LASSO
This norm l1 induces sparsity in the weight terms.
How?
For example, [1, 0]T
2
= [1/
√
2, 1/
√
2]T
2
= 1.
In the other case, [1, 0]T
1
= 1 < [1/
√
2, 1/
√
2]T
2
=
√
2.
31 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-71-320.jpg)
![Remark
This criterion is know as the LASSO
This norm l1 induces sparsity in the weight terms.
How?
For example, [1, 0]T
2
= [1/
√
2, 1/
√
2]T
2
= 1.
In the other case, [1, 0]T
1
= 1 < [1/
√
2, 1/
√
2]T
2
=
√
2.
31 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-72-320.jpg)
![Remark
This criterion is know as the LASSO
This norm l1 induces sparsity in the weight terms.
How?
For example, [1, 0]T
2
= [1/
√
2, 1/
√
2]T
2
= 1.
In the other case, [1, 0]T
1
= 1 < [1/
√
2, 1/
√
2]T
2
=
√
2.
31 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-73-320.jpg)




















![The EM trick
How do we do this?
This is done by regarding τ = [τ1, ..., τk] as the hidden/missing data
Then, if we could observe τ, complete log-posterior log p (β, σ2
|y, τ)
can be easily calculated
p β, σ2
|y, τ ∝ p y|β, σ2
p (β|τ) p σ2
(30)
Where
p y|β, σ2 ∼ N β, σ2
p (β|0, τ) ∼ N (0, τ)
44 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-99-320.jpg)
![The EM trick
How do we do this?
This is done by regarding τ = [τ1, ..., τk] as the hidden/missing data
Then, if we could observe τ, complete log-posterior log p (β, σ2
|y, τ)
can be easily calculated
p β, σ2
|y, τ ∝ p y|β, σ2
p (β|τ) p σ2
(30)
Where
p y|β, σ2 ∼ N β, σ2
p (β|0, τ) ∼ N (0, τ)
44 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-100-320.jpg)
![The EM trick
How do we do this?
This is done by regarding τ = [τ1, ..., τk] as the hidden/missing data
Then, if we could observe τ, complete log-posterior log p (β, σ2
|y, τ)
can be easily calculated
p β, σ2
|y, τ ∝ p y|β, σ2
p (β|τ) p σ2
(30)
Where
p y|β, σ2 ∼ N β, σ2
p (β|0, τ) ∼ N (0, τ)
44 / 66](https://image.slidesharecdn.com/04-151212035438/85/08-Machine-Learning-Maximum-Aposteriori-101-320.jpg)