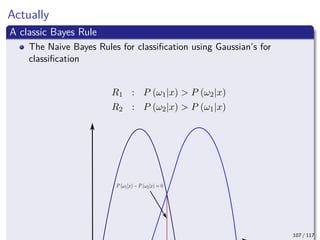
This document outlines an introduction to Bayesian estimation. It discusses key concepts like the likelihood principle, sufficiency, and Bayesian inference. The likelihood principle states that all experimental information about an unknown parameter is contained within the likelihood function. An example is provided testing the fairness of a coin using different data collection scenarios to illustrate how the likelihood function remains the same. The document also discusses the history of the likelihood principle and provides an outline of topics to be covered.

1. Introduction to Mathematics for AI
Bayesian Estimation
Andres Mendez-Vazquez
May 22, 2020
1 / 117

2. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
2 / 117

3. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
3 / 117

4. The Basis of Bayesian Inference
A Basic setup
Let f(x|θ) be a conditional distribution for X given the unknown
parameter θ.
For the observed data, X = x, the function (θ) = f(x|θ)
It is called the likelihood function!!!
The name likelihood implies that, given x, the value of θ
It is more likely to be the true parameter than θ , if
f (x|θ) > f x|θ
4 / 117

5. The Basis of Bayesian Inference
A Basic setup
Let f(x|θ) be a conditional distribution for X given the unknown
parameter θ.
For the observed data, X = x, the function (θ) = f(x|θ)
It is called the likelihood function!!!
The name likelihood implies that, given x, the value of θ
It is more likely to be the true parameter than θ , if
f (x|θ) > f x|θ
4 / 117

6. The Basis of Bayesian Inference
A Basic setup
Let f(x|θ) be a conditional distribution for X given the unknown
parameter θ.
For the observed data, X = x, the function (θ) = f(x|θ)
It is called the likelihood function!!!
The name likelihood implies that, given x, the value of θ
It is more likely to be the true parameter than θ , if
f (x|θ) > f x|θ
4 / 117

7. Basically
We are talking about optimization functions
Where optimals are being loked upon...
Definition
An optimal solution to an optimization poroblems is the feasible
solution with the largest objective function value (for a maximization
problem).
5 / 117

8. Basically
We are talking about optimization functions
Where optimals are being loked upon...
Definition
An optimal solution to an optimization poroblems is the feasible
solution with the largest objective function value (for a maximization
problem).
5 / 117

9. Likelihood Principle
Remarks
In the inference about θ, after x is observed, all relevant
experimental information is contained in the likelihood function
for the observed x.
There is an interesting example quoted by Lindley and Phillips in
1976 [1]
Originally by Leonard Savage
Leonard Savage
Leonard Jimmie Savage (born Leonard Ogashevitz; 20 November
1917 – 1 November 1971) was an American mathematician and
statistician.
Economist Milton Friedman said Savage was "one of the few people I
have met whom I would unhesitatingly call a genius.
6 / 117

10. Likelihood Principle
Remarks
In the inference about θ, after x is observed, all relevant
experimental information is contained in the likelihood function
for the observed x.
There is an interesting example quoted by Lindley and Phillips in
1976 [1]
Originally by Leonard Savage
Leonard Savage
Leonard Jimmie Savage (born Leonard Ogashevitz; 20 November
1917 – 1 November 1971) was an American mathematician and
statistician.
Economist Milton Friedman said Savage was "one of the few people I
have met whom I would unhesitatingly call a genius.
6 / 117

11. Likelihood Principle
Remarks
In the inference about θ, after x is observed, all relevant
experimental information is contained in the likelihood function
for the observed x.
There is an interesting example quoted by Lindley and Phillips in
1976 [1]
Originally by Leonard Savage
Leonard Savage
Leonard Jimmie Savage (born Leonard Ogashevitz; 20 November
1917 – 1 November 1971) was an American mathematician and
statistician.
Economist Milton Friedman said Savage was "one of the few people I
have met whom I would unhesitatingly call a genius.
6 / 117

12. History
Something Notable
The likelihood principle was first identified by that name in print in
1962 (Barnard et al., Birnbaum, and Savage et al.),
However Fisher
It was already using a version of it in 1920’s.
However, versions of it can be tracked to
To the mid-1700s
It seems to have become a commonplace among natural philosophers
that problems of observational error were susceptible to mathematical
description.
7 / 117

13. History
Something Notable
The likelihood principle was first identified by that name in print in
1962 (Barnard et al., Birnbaum, and Savage et al.),
However Fisher
It was already using a version of it in 1920’s.
However, versions of it can be tracked to
To the mid-1700s
It seems to have become a commonplace among natural philosophers
that problems of observational error were susceptible to mathematical
description.
7 / 117

14. History
Something Notable
The likelihood principle was first identified by that name in print in
1962 (Barnard et al., Birnbaum, and Savage et al.),
However Fisher
It was already using a version of it in 1920’s.
However, versions of it can be tracked to
To the mid-1700s
It seems to have become a commonplace among natural philosophers
that problems of observational error were susceptible to mathematical
description.
7 / 117

15. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
8 / 117

16. Testing Fairness
Basic Setup
Suppose we are interested in testing θ, the unknown probability of
heads for possibly biased coin.
Suppose the following Hypothesis
H0 : θ = 1/2 v.s. H1 : θ > 1/2
Then
An experiment is conducted and 9 heads and 3 tails are observed.
Not enough information to fully specify f (x|θ)
9 / 117

17. Testing Fairness
Basic Setup
Suppose we are interested in testing θ, the unknown probability of
heads for possibly biased coin.
Suppose the following Hypothesis
H0 : θ = 1/2 v.s. H1 : θ > 1/2
Then
An experiment is conducted and 9 heads and 3 tails are observed.
Not enough information to fully specify f (x|θ)
9 / 117

18. Testing Fairness
Basic Setup
Suppose we are interested in testing θ, the unknown probability of
heads for possibly biased coin.
Suppose the following Hypothesis
H0 : θ = 1/2 v.s. H1 : θ > 1/2
Then
An experiment is conducted and 9 heads and 3 tails are observed.
Not enough information to fully specify f (x|θ)
9 / 117

19. Scenario 1
Based on rashomonian analysis
The classic Akira Kurosawa film Rashomon has become a shorthand
for the lie of objective truth—what you see, basically, depends on
where you stand.
Number of flips, n = 12 is predetermined
Then number of heads X is binomial B(n, θ), with probability mass
function:
Pθ (X = x) = f (x|θ) =
n
x
θx
(1 − θ)n−x
10 / 117

20. Scenario 1
Based on rashomonian analysis
The classic Akira Kurosawa film Rashomon has become a shorthand
for the lie of objective truth—what you see, basically, depends on
where you stand.
Number of flips, n = 12 is predetermined
Then number of heads X is binomial B(n, θ), with probability mass
function:
Pθ (X = x) = f (x|θ) =
n
x
θx
(1 − θ)n−x
10 / 117

21. Therefore
We have
Pθ (X = x) =
12
9
θ9
(1 − θ)3
Thus
We can use the p − value for testing the hypothesis.
11 / 117

22. Therefore
We have
Pθ (X = x) =
12
9
θ9
(1 − θ)3
Thus
We can use the p − value for testing the hypothesis.
11 / 117

23. Then if we use the following p − value analysis
Definition [2, 3]
The p-value is defined as the probability, under the null hypothesis H0
about the unknown distribution F of the random variable X.
Very Unlike
Observation
Very Unlike
Observation
P-Value
More Likely Observation
Set of Possible Results
ProbabilityDensity
Observed
Data Point
12 / 117

24. Therefore
For a frequentist, the p − value of the test is
P (X ≥ 9|H0) =
12
x=9
12
x
1
2
x
1
2
12−x
= 0.073
Given an α = 0.05
Then, H0 is not rejected...
13 / 117

25. Therefore
For a frequentist, the p − value of the test is
P (X ≥ 9|H0) =
12
x=9
12
x
1
2
x
1
2
12−x
= 0.073
Given an α = 0.05
Then, H0 is not rejected...
13 / 117

26. Scenario 2
Number of tails (successes) 3 is predetermined
i.e, the flipping is continued until 3 tails are observed.
Then you have a Negative Binomial with r the number of failures
f (x|θ) =
k + r − 1
k − 1
(1 − θ)k
θr
Thus, we have
f (x|θ) =
3 + 9 − 1
3 − 1
(1 − θ)3
θ9
= 55 (1 − θ)3
θ9
14 / 117

27. Scenario 2
Number of tails (successes) 3 is predetermined
i.e, the flipping is continued until 3 tails are observed.
Then you have a Negative Binomial with r the number of failures
f (x|θ) =
k + r − 1
k − 1
(1 − θ)k
θr
Thus, we have
f (x|θ) =
3 + 9 − 1
3 − 1
(1 − θ)3
θ9
= 55 (1 − θ)3
θ9
14 / 117

28. Scenario 2
Number of tails (successes) 3 is predetermined
i.e, the flipping is continued until 3 tails are observed.
Then you have a Negative Binomial with r the number of failures
f (x|θ) =
k + r − 1
k − 1
(1 − θ)k
θr
Thus, we have
f (x|θ) =
3 + 9 − 1
3 − 1
(1 − θ)3
θ9
= 55 (1 − θ)3
θ9
14 / 117

29. In a similar way
We have
P (X ≥ 9|H0) =
∞
x=9
3 + x − 1
3 − 1
1
2
x
1
2
3
= 0.0327
Thus, the hypothesis H0 is rejected
But this change in decision is not caused by observations.
However, all relevant information is in the likelihood!!!
(θ) ∝ θ9
(1 − θ)3
15 / 117

30. In a similar way
We have
P (X ≥ 9|H0) =
∞
x=9
3 + x − 1
3 − 1
1
2
x
1
2
3
= 0.0327
Thus, the hypothesis H0 is rejected
But this change in decision is not caused by observations.
However, all relevant information is in the likelihood!!!
(θ) ∝ θ9
(1 − θ)3
15 / 117

31. In a similar way
We have
P (X ≥ 9|H0) =
∞
x=9
3 + x − 1
3 − 1
1
2
x
1
2
3
= 0.0327
Thus, the hypothesis H0 is rejected
But this change in decision is not caused by observations.
However, all relevant information is in the likelihood!!!
(θ) ∝ θ9
(1 − θ)3
15 / 117

32. Remark
Edwards, Lindman, and Savage remarked
The likelihood principle emphasized in Bayesian statistics implies,
among other things, that the rules governing when data collection
stops are irrelevant to data interpretation.
Therefore
It is entirely appropriate to collect data until a point has been proven
or disproven, or until the data collector runs out of time, money, or
patience.
16 / 117

33. Remark
Edwards, Lindman, and Savage remarked
The likelihood principle emphasized in Bayesian statistics implies,
among other things, that the rules governing when data collection
stops are irrelevant to data interpretation.
Therefore
It is entirely appropriate to collect data until a point has been proven
or disproven, or until the data collector runs out of time, money, or
patience.
16 / 117

34. Thus
Likelihood Principle [4]
The Likelihood principle (LP) asserts that for inference on an
unknown quantity θ, all of the evidence from any observation X = x
with distribution X ∼ f (x|θ) lies in the likelihood function
L (θ|x) ∝ f (x|θ) , θ ∈ Θ
17 / 117

35. Thus
Something Notable
The interpretation of LP hinges on the rather subtle point of allowing
any observable X to draw conclusions about θ.
Therefore
If there two ways to gather infromation about theta, wither
X ∼ f (x|θ) or with Y ∼ g (x|θ)
with X = x and Y = y then
L (θ|x) = η × L (θ|y) , ∀θ ∈ Θ
18 / 117

36. Thus
Something Notable
The interpretation of LP hinges on the rather subtle point of allowing
any observable X to draw conclusions about θ.
Therefore
If there two ways to gather infromation about theta, wither
X ∼ f (x|θ) or with Y ∼ g (x|θ)
with X = x and Y = y then
L (θ|x) = η × L (θ|y) , ∀θ ∈ Θ
18 / 117

37. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
19 / 117

38. In the case of Learning
Yes, we use the principle, but we add the idea of independence
A trick to assume a set of samples x1, x2, ..., xN such that
xi ∼ f (X|θ)
Then, as we have seen it
L (θ) = f (x1, x2, ..., xN |θ) =
N
i=1
f (xi|θ)
20 / 117

39. In the case of Learning
Yes, we use the principle, but we add the idea of independence
A trick to assume a set of samples x1, x2, ..., xN such that
xi ∼ f (X|θ)
Then, as we have seen it
L (θ) = f (x1, x2, ..., xN |θ) =
N
i=1
f (xi|θ)
20 / 117

40. Example, p (x|ωj) ∼ N µj, Σj
L (θj) = log n
j=1 p (xj|θj)
21 / 117

41. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
22 / 117

42. The Basics
Sufficiency Principle
An statistic is sufficient with respect to a statistical model and its
associated unknown parameter if
"no other statistic that can be calculated from the same sample
provides any additional information as to the value of the parameter"[5]
However, as always
We want a definition to build upon it... as always
23 / 117

43. The Basics
Sufficiency Principle
An statistic is sufficient with respect to a statistical model and its
associated unknown parameter if
"no other statistic that can be calculated from the same sample
provides any additional information as to the value of the parameter"[5]
However, as always
We want a definition to build upon it... as always
23 / 117

44. A Basic Definition
Definition
A statistic t = T(X) is sufficient for underlying parameter θ precisely
if the conditional probability distribution of the data X, given the
statistic t = T(X), does not depend on the parameter θ [6].
Something Notable
This agreement is non-philosophical, it is rather a consequence of
mathematics (measure theoretic considerations).
24 / 117

45. A Basic Definition
Definition
A statistic t = T(X) is sufficient for underlying parameter θ precisely
if the conditional probability distribution of the data X, given the
statistic t = T(X), does not depend on the parameter θ [6].
Something Notable
This agreement is non-philosophical, it is rather a consequence of
mathematics (measure theoretic considerations).
24 / 117

46. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
25 / 117

47. Fisher’s Factorization Theorem
Theorem
Let f (x|θ) be the density or mass function for the random vector x,
parametrized by the vector theta. The statistic t = T (x) is sufficient
for θ if and only if there exist functions a (x) (not depending on θ)
and b (t|θ) such that ()
f (x|θ) = a (x) b (t, θ)
for all possible values of x.
26 / 117

48. Proof
First ⇒ (We will look only to the discrete case [7])
Suppose t = T (x) is sufficient for θ. Then, by definition
f (x|θ, T (x) = t) is independient of θ
Let f (x, t|θ) denote the joint density function or mass function for
(X, T (X))
Observe f (x|θ) = f (x, t|θ) then we have
f (x|θ) = f (x, t|θ)
= f (x|θ, t) f (t|θ) Bayesian
= a (x)
f (x|t)
b (t, θ)
f (t|θ)
Independence
27 / 117

49. Proof
First ⇒ (We will look only to the discrete case [7])
Suppose t = T (x) is sufficient for θ. Then, by definition
f (x|θ, T (x) = t) is independient of θ
Let f (x, t|θ) denote the joint density function or mass function for
(X, T (X))
Observe f (x|θ) = f (x, t|θ) then we have
f (x|θ) = f (x, t|θ)
= f (x|θ, t) f (t|θ) Bayesian
= a (x)
f (x|t)
b (t, θ)
f (t|θ)
Independence
27 / 117

50. Proof
First ⇒ (We will look only to the discrete case [7])
Suppose t = T (x) is sufficient for θ. Then, by definition
f (x|θ, T (x) = t) is independient of θ
Let f (x, t|θ) denote the joint density function or mass function for
(X, T (X))
Observe f (x|θ) = f (x, t|θ) then we have
f (x|θ) = f (x, t|θ)
= f (x|θ, t) f (t|θ) Bayesian
= a (x)
f (x|t)
b (t, θ)
f (t|θ)
Independence
27 / 117

51. Proof
First ⇒ (We will look only to the discrete case [7])
Suppose t = T (x) is sufficient for θ. Then, by definition
f (x|θ, T (x) = t) is independient of θ
Let f (x, t|θ) denote the joint density function or mass function for
(X, T (X))
Observe f (x|θ) = f (x, t|θ) then we have
f (x|θ) = f (x, t|θ)
= f (x|θ, t) f (t|θ) Bayesian
= a (x)
f (x|t)
b (t, θ)
f (t|θ)
Independence
27 / 117

52. Proof
First ⇒ (We will look only to the discrete case [7])
Suppose t = T (x) is sufficient for θ. Then, by definition
f (x|θ, T (x) = t) is independient of θ
Let f (x, t|θ) denote the joint density function or mass function for
(X, T (X))
Observe f (x|θ) = f (x, t|θ) then we have
f (x|θ) = f (x, t|θ)
= f (x|θ, t) f (t|θ) Bayesian
= a (x)
f (x|t)
b (t, θ)
f (t|θ)
Independence
27 / 117

53. Now, for the case ⇐
Suppose the probability mass function for x can be written
f (x|θ) = a (x) b (x|θ) where t = T (x)
The probability mass function for t is obtained by summing fθ (x, t)
over all x such that T (x) = t
f (t|θ) =
T(x)=t
f (x, t|θ)
=
T(x)=t
f (x|θ) ← independence over t
=
T(x)=t
a (x) bθ (x)
28 / 117

54. Now, for the case ⇐
Suppose the probability mass function for x can be written
f (x|θ) = a (x) b (x|θ) where t = T (x)
The probability mass function for t is obtained by summing fθ (x, t)
over all x such that T (x) = t
f (t|θ) =
T(x)=t
f (x, t|θ)
=
T(x)=t
f (x|θ) ← independence over t
=
T(x)=t
a (x) bθ (x)
28 / 117

55. Now, for the case ⇐
Suppose the probability mass function for x can be written
f (x|θ) = a (x) b (x|θ) where t = T (x)
The probability mass function for t is obtained by summing fθ (x, t)
over all x such that T (x) = t
f (t|θ) =
T(x)=t
f (x, t|θ)
=
T(x)=t
f (x|θ) ← independence over t
=
T(x)=t
a (x) bθ (x)
28 / 117

56. Now, for the case ⇐
Suppose the probability mass function for x can be written
f (x|θ) = a (x) b (x|θ) where t = T (x)
The probability mass function for t is obtained by summing fθ (x, t)
over all x such that T (x) = t
f (t|θ) =
T(x)=t
f (x, t|θ)
=
T(x)=t
f (x|θ) ← independence over t
=
T(x)=t
a (x) bθ (x)
28 / 117

57. Therefore, we have that
The conditional mass function of x given t
f (x|θ, t) =
f (x, t|θ)
f (t|θ)
=
f (x|θ)
f (t|θ)
=
a (x) bθ (x)
T(x)=t a (x) bθ (x)
=
a (x)
T(x)=t a (x)
This last expression does not depend on θ
t is a sufficient statistic for θ.
29 / 117

58. Therefore, we have that
The conditional mass function of x given t
f (x|θ, t) =
f (x, t|θ)
f (t|θ)
=
f (x|θ)
f (t|θ)
=
a (x) bθ (x)
T(x)=t a (x) bθ (x)
=
a (x)
T(x)=t a (x)
This last expression does not depend on θ
t is a sufficient statistic for θ.
29 / 117

59. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
30 / 117

60. Using the Bernoulli Distribution
xn ∼Bernoulli(θ) are i.d.d. ∀n = 1, ..., N
f (x1, .., xN |θ) =
N
n=1
θxn
(1 − θ)1−xn
= θk
(1 − θ)N−k
k = N
n=1 xn
Now, if we have the following choices
a (x) = 1 and bθ (k) = θk
(1 − θ)N−k
31 / 117

61. Using the Bernoulli Distribution
xn ∼Bernoulli(θ) are i.d.d. ∀n = 1, ..., N
f (x1, .., xN |θ) =
N
n=1
θxn
(1 − θ)1−xn
= θk
(1 − θ)N−k
k = N
n=1 xn
Now, if we have the following choices
a (x) = 1 and bθ (k) = θk
(1 − θ)N−k
31 / 117

62. Therefore
Then choosing
T (x1, .., xN ) = N
n=1 xn = k
By the Fisher-Neyman Factorization Theorem
k is sufficient for θ
32 / 117

63. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
33 / 117

64. Something Quite Interesting
The Fisher-Neyman factorization lemma states
The likelihood can be represented as
(θ) = f (x|θ) = a (x) bθ (T (x))
34 / 117

65. If the likelihood principle is adopted
All inference about θ should depend on sufficient statistics
Since (θ) ∝ bθ (T (x))
Sufficiency Principle
Let the two different observations x and y have the same values
T (x) = T (y), of a statistics sufficient for family f (·|θ). Then the
inferences about θ based on x and y should be the same.
35 / 117

66. If the likelihood principle is adopted
All inference about θ should depend on sufficient statistics
Since (θ) ∝ bθ (T (x))
Sufficiency Principle
Let the two different observations x and y have the same values
T (x) = T (y), of a statistics sufficient for family f (·|θ). Then the
inferences about θ based on x and y should be the same.
35 / 117

67. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
36 / 117

68. Conditionality Perspective
We have that
Conditional perspective concerns reporting data specific measures
of accuracy.
In contrast to the frequentist approach
Performance of statistical procedures are judged looking at the
observed data.
37 / 117

69. Conditionality Perspective
We have that
Conditional perspective concerns reporting data specific measures
of accuracy.
In contrast to the frequentist approach
Performance of statistical procedures are judged looking at the
observed data.
37 / 117

70. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
38 / 117

71. Example
Consider estimating θ in the model
P (X = θ − 1|θ) = P (X = θ + 1|θ) with θ ∈ R
on basis of two observations, X1 and X2 .
The procedure suggested is
δ (X) =
X1+X2
2 if X1 = X2
X1 − 1 if X1 = X2
39 / 117

72. Example
Consider estimating θ in the model
P (X = θ − 1|θ) = P (X = θ + 1|θ) with θ ∈ R
on basis of two observations, X1 and X2 .
The procedure suggested is
δ (X) =
X1+X2
2 if X1 = X2
X1 − 1 if X1 = X2
39 / 117

73. Therefore
To a frequentist, this procedure has confidence
To a frequentist, this procedure has confidence of 75% for all θ, i.e.,
P (δ (X) = θ) = 0.75.
The conditionalist would report the confidence
100% if observed data in hand are different
50% if the observations coincide
40 / 117

74. Therefore
To a frequentist, this procedure has confidence
To a frequentist, this procedure has confidence of 75% for all θ, i.e.,
P (δ (X) = θ) = 0.75.
The conditionalist would report the confidence
100% if observed data in hand are different
50% if the observations coincide
40 / 117

75. Then
Conditionality Principle
If an experiment concerning the inference about θ is chosen from a
collection of possible experiments, independently of θ, then any
experiment not chosen is irrelevant to the inference.
41 / 117

76. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
42 / 117

77. Not a good idea to integrate with respect to sample space
What?
A perfectly valid hypothesis can be rejected because the
test failed to account for unlikely data that had not been
observed...
43 / 117

78. The Lindley Paradox
Suppose y|θ ∼ N θ, 1
n
We wish to test H0 : θ = 0 vs the two sided alternative.
Suppose a Bayesian puts the prior P (θ = 0) = P (θ = 0) = 1
2
The 1
2 is uniformly spread over the interval [−M/2, M/2].
Suppose n = 40, 000 and y = 0.01 are observed
So,
√
ny = 2
44 / 117

79. The Lindley Paradox
Suppose y|θ ∼ N θ, 1
n
We wish to test H0 : θ = 0 vs the two sided alternative.
Suppose a Bayesian puts the prior P (θ = 0) = P (θ = 0) = 1
2
The 1
2 is uniformly spread over the interval [−M/2, M/2].
Suppose n = 40, 000 and y = 0.01 are observed
So,
√
ny = 2
44 / 117

80. The Lindley Paradox
Suppose y|θ ∼ N θ, 1
n
We wish to test H0 : θ = 0 vs the two sided alternative.
Suppose a Bayesian puts the prior P (θ = 0) = P (θ = 0) = 1
2
The 1
2 is uniformly spread over the interval [−M/2, M/2].
Suppose n = 40, 000 and y = 0.01 are observed
So,
√
ny = 2
44 / 117

81. Therefore
Classical statistician
She/he rejects H0 at level α = 0.05
Posterior odds in favor of H0 are 11 if M = 1
We will look at this... no worries, but Bayesian Statistician will
choose H0
45 / 117

82. Therefore
Classical statistician
She/he rejects H0 at level α = 0.05
Posterior odds in favor of H0 are 11 if M = 1
We will look at this... no worries, but Bayesian Statistician will
choose H0
45 / 117

83. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
46 / 117

84. Using our likelihood
We have our function
(θ) = f (x|θ)
Here
The parameter θ is supported by the parameter space Θ and
considered a random variable.
The random variable θ has a distribution π (θ) that is called the prior.
47 / 117

85. Using our likelihood
We have our function
(θ) = f (x|θ)
Here
The parameter θ is supported by the parameter space Θ and
considered a random variable.
The random variable θ has a distribution π (θ) that is called the prior.
47 / 117

86. Not only that
We have the following
We can play a hierarchy game
θ ∼ π (θ|τ) where τ is called a hyperparameter
This give us an idea about the marginals
m (x) =
Θ
f (x, θ) =
Θ
f (x|θ) π (θ) dθ
48 / 117

87. Not only that
We have the following
We can play a hierarchy game
θ ∼ π (θ|τ) where τ is called a hyperparameter
This give us an idea about the marginals
m (x) =
Θ
f (x, θ) =
Θ
f (x|θ) π (θ) dθ
48 / 117

88. What about the posterior?
We have the following
f (θ|x) =
f (x, θ)
m (x)
=
f (x|θ) π (θ)
m (x)
=
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
49 / 117

89. What about the posterior?
We have the following
f (θ|x) =
f (x, θ)
m (x)
=
f (x|θ) π (θ)
m (x)
=
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
49 / 117

90. What about the posterior?
We have the following
f (θ|x) =
f (x, θ)
m (x)
=
f (x|θ) π (θ)
m (x)
=
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
49 / 117

91. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
50 / 117

92. An interesting case
Suppose that the observations are coming from N (θ, σ2
1)
Assume prior on θ is N (σ2, σ2)
Then, under this setup
the normal/normal model, the posterior is f (θ|X1, ..., Xn) = f θ|X
51 / 117

93. An interesting case
Suppose that the observations are coming from N (θ, σ2
1)
Assume prior on θ is N (σ2, σ2)
Then, under this setup
the normal/normal model, the posterior is f (θ|X1, ..., Xn) = f θ|X
51 / 117

94. The connection
Lemma
Suppose the sufficient statistics T = T (X1, ..., Xn) exist. Then
f (θ|X1, ..., Xn) = f (θ|T) .
52 / 117

95. Proof
Factorization theorem for sufficient statistics is
f (x|θ) = bθ (t) a (x)
Where
t = T (x) and a (x) do not depend on θ.
53 / 117

96. Proof
Factorization theorem for sufficient statistics is
f (x|θ) = bθ (t) a (x)
Where
t = T (x) and a (x) do not depend on θ.
53 / 117

97. Furhtermore
Thus
π (θ|x) =
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
=
bθ (t) a (x) π (θ)
Θ bθ (t) a (x) π (θ) dθ
=
bθ (t) π (θ)
Θ bθ (t) π (θ) dθ
54 / 117

98. Furhtermore
Thus
π (θ|x) =
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
=
bθ (t) a (x) π (θ)
Θ bθ (t) a (x) π (θ) dθ
=
bθ (t) π (θ)
Θ bθ (t) π (θ) dθ
54 / 117

99. Furhtermore
Thus
π (θ|x) =
f (x|θ) π (θ)
Θ f (x|θ) π (θ) dθ
=
bθ (t) a (x) π (θ)
Θ bθ (t) a (x) π (θ) dθ
=
bθ (t) π (θ)
Θ bθ (t) π (θ) dθ
54 / 117

100. The
Multiply and divide by φ (t)
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
π (θ) f (t|θ)
Θ π (θ) f (t|θ) dθ
= π (θ|t)
55 / 117

101. The
Multiply and divide by φ (t)
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
π (θ) f (t|θ)
Θ π (θ) f (t|θ) dθ
= π (θ|t)
55 / 117

102. The
Multiply and divide by φ (t)
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
bθ (t) π (θ) φ (t)
Θ bθ (t) π (θ) φ (t) dθ
=
π (θ) f (t|θ)
Θ π (θ) f (t|θ) dθ
= π (θ|t)
55 / 117

103. Here, we have
The following equations
f (t|θ) =
x:T(x)=t
f (x|θ) dx =
x:T(x)=t
bθ (t) a (x) dx
Then
x:T(x)=t
bθ (t) a (x) dx = bθ (t)
x:T(x)=t
a (x) dx = bθ (t) φ (t)
56 / 117

104. Here, we have
The following equations
f (t|θ) =
x:T(x)=t
f (x|θ) dx =
x:T(x)=t
bθ (t) a (x) dx
Then
x:T(x)=t
bθ (t) a (x) dx = bθ (t)
x:T(x)=t
a (x) dx = bθ (t) φ (t)
56 / 117

105. Then
We have the following definition
Definition
The statistics T = T(X) is sufficient (in the Bayesian sense) if for
any prior the resulting posterior satisfies
π (θ|X) = π (θ|T)
This is equivalent to the classic definition on sufficient statistics
Theorem
T is sufficient in the Bayesian sense if and only if it is sufficient in the
usual sense.
57 / 117

106. Then
We have the following definition
Definition
The statistics T = T(X) is sufficient (in the Bayesian sense) if for
any prior the resulting posterior satisfies
π (θ|X) = π (θ|T)
This is equivalent to the classic definition on sufficient statistics
Theorem
T is sufficient in the Bayesian sense if and only if it is sufficient in the
usual sense.
57 / 117

107. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
58 / 117

108. Something quite important
Something Notable
The posterior is the ultimate experimental summary for a Bayesian.
Not only that
The location measures (especially the mean) of the posterior are of
importance.
There is an important idea
The posterior mode and median are also Bayes estimators under
different loss functions!!!
59 / 117

109. Something quite important
Something Notable
The posterior is the ultimate experimental summary for a Bayesian.
Not only that
The location measures (especially the mean) of the posterior are of
importance.
There is an important idea
The posterior mode and median are also Bayes estimators under
different loss functions!!!
59 / 117

110. Something quite important
Something Notable
The posterior is the ultimate experimental summary for a Bayesian.
Not only that
The location measures (especially the mean) of the posterior are of
importance.
There is an important idea
The posterior mode and median are also Bayes estimators under
different loss functions!!!
59 / 117

111. Furthermore
Generalized Maximum Likelihood Estimator AKA MAP (Maximum
Aposteriori)
The generalized MLE is the largest mode of the π (θ|x).
60 / 117

112. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
61 / 117

113. What can we do?
We can specify a distribution
Then, learn the parameters
Remember the Bayesian Rule
p (Θ|X) =
p (X|Θ) p (Θ)
p (X)
(1)
We seek that value for Θ, called ΘMAP
It allows to maximize the posterior p (Θ|X)
62 / 117

114. What can we do?
We can specify a distribution
Then, learn the parameters
Remember the Bayesian Rule
p (Θ|X) =
p (X|Θ) p (Θ)
p (X)
(1)
We seek that value for Θ, called ΘMAP
It allows to maximize the posterior p (Θ|X)
62 / 117

115. What can we do?
We can specify a distribution
Then, learn the parameters
Remember the Bayesian Rule
p (Θ|X) =
p (X|Θ) p (Θ)
p (X)
(1)
We seek that value for Θ, called ΘMAP
It allows to maximize the posterior p (Θ|X)
62 / 117

116. Therefore
We can use this idea of maximizing the posterior
To obtain the distribution through the Maximum a Posteriori
63 / 117

117. Development of the solution
We look to maximize ΘMAP
ΘMAP = argmax
Θ
p (Θ|X)
= argmax
Θ
p (X|Θ) p (Θ)
P (X)
≈ argmax
Θ
p (X|Θ) p (Θ)
= argmax
Θ xi∈X
p (xi|Θ) p (Θ)
P (X) can be removed because it has no functional relation with Θ.
64 / 117

118. Development of the solution
We look to maximize ΘMAP
ΘMAP = argmax
Θ
p (Θ|X)
= argmax
Θ
p (X|Θ) p (Θ)
P (X)
≈ argmax
Θ
p (X|Θ) p (Θ)
= argmax
Θ xi∈X
p (xi|Θ) p (Θ)
P (X) can be removed because it has no functional relation with Θ.
64 / 117

119. Development of the solution
We look to maximize ΘMAP
ΘMAP = argmax
Θ
p (Θ|X)
= argmax
Θ
p (X|Θ) p (Θ)
P (X)
≈ argmax
Θ
p (X|Θ) p (Θ)
= argmax
Θ xi∈X
p (xi|Θ) p (Θ)
P (X) can be removed because it has no functional relation with Θ.
64 / 117

120. Development of the solution
We look to maximize ΘMAP
ΘMAP = argmax
Θ
p (Θ|X)
= argmax
Θ
p (X|Θ) p (Θ)
P (X)
≈ argmax
Θ
p (X|Θ) p (Θ)
= argmax
Θ xi∈X
p (xi|Θ) p (Θ)
P (X) can be removed because it has no functional relation with Θ.
64 / 117

121. Development of the solution
We look to maximize ΘMAP
ΘMAP = argmax
Θ
p (Θ|X)
= argmax
Θ
p (X|Θ) p (Θ)
P (X)
≈ argmax
Θ
p (X|Θ) p (Θ)
= argmax
Θ xi∈X
p (xi|Θ) p (Θ)
P (X) can be removed because it has no functional relation with Θ.
64 / 117

122. We can make this easier
Use logarithms
ΘMAP = argmax
Θ


xi∈X
log p (xi|Θ) + log p (Θ)

 (2)
65 / 117

123. What Does the MAP Estimate Get?
Something Notable
The MAP estimate allows us to inject into the estimation calculation our
prior beliefs regarding the parameters values in Θ.
For example
Let’s conduct N independent trials of the following Bernoulli experiment
with q parameter:
We will ask each individual we run into in the hallway whether they
will vote PRI or PAN in the next presidential election.
With probability q to vote PRI
Where the values of xi is either PRI or PAN.
66 / 117

124. What Does the MAP Estimate Get?
Something Notable
The MAP estimate allows us to inject into the estimation calculation our
prior beliefs regarding the parameters values in Θ.
For example
Let’s conduct N independent trials of the following Bernoulli experiment
with q parameter:
We will ask each individual we run into in the hallway whether they
will vote PRI or PAN in the next presidential election.
With probability q to vote PRI
Where the values of xi is either PRI or PAN.
66 / 117

125. What Does the MAP Estimate Get?
Something Notable
The MAP estimate allows us to inject into the estimation calculation our
prior beliefs regarding the parameters values in Θ.
For example
Let’s conduct N independent trials of the following Bernoulli experiment
with q parameter:
We will ask each individual we run into in the hallway whether they
will vote PRI or PAN in the next presidential election.
With probability q to vote PRI
Where the values of xi is either PRI or PAN.
66 / 117

126. What Does the MAP Estimate Get?
Something Notable
The MAP estimate allows us to inject into the estimation calculation our
prior beliefs regarding the parameters values in Θ.
For example
Let’s conduct N independent trials of the following Bernoulli experiment
with q parameter:
We will ask each individual we run into in the hallway whether they
will vote PRI or PAN in the next presidential election.
With probability q to vote PRI
Where the values of xi is either PRI or PAN.
66 / 117

127. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
67 / 117

128. First the Maximum Likelihood Estimate
Samples
X = xi =
PAN
PRI
i = 1, ..., N (3)
The log likelihood function
log p (X|q) =
N
i=1
log p (xi|q)
=
i
log p (xi = PRI|q) + ...
i
log p (xi = PAN|1 − q)
=nPRI log (q) + (N − nPRI) log (1 − q)
Where nPRI are the numbers of individuals who are planning to vote PRI
this fall 68 / 117

129. First the Maximum Likelihood Estimate
Samples
X = xi =
PAN
PRI
i = 1, ..., N (3)
The log likelihood function
log p (X|q) =
N
i=1
log p (xi|q)
=
i
log p (xi = PRI|q) + ...
i
log p (xi = PAN|1 − q)
=nPRI log (q) + (N − nPRI) log (1 − q)
Where nPRI are the numbers of individuals who are planning to vote PRI
this fall 68 / 117

130. First the Maximum Likelihood Estimate
Samples
X = xi =
PAN
PRI
i = 1, ..., N (3)
The log likelihood function
log p (X|q) =
N
i=1
log p (xi|q)
=
i
log p (xi = PRI|q) + ...
i
log p (xi = PAN|1 − q)
=nPRI log (q) + (N − nPRI) log (1 − q)
Where nPRI are the numbers of individuals who are planning to vote PRI
this fall 68 / 117

131. First the Maximum Likelihood Estimate
Samples
X = xi =
PAN
PRI
i = 1, ..., N (3)
The log likelihood function
log p (X|q) =
N
i=1
log p (xi|q)
=
i
log p (xi = PRI|q) + ...
i
log p (xi = PAN|1 − q)
=nPRI log (q) + (N − nPRI) log (1 − q)
Where nPRI are the numbers of individuals who are planning to vote PRI
this fall 68 / 117

132. First the Maximum Likelihood Estimate
Samples
X = xi =
PAN
PRI
i = 1, ..., N (3)
The log likelihood function
log p (X|q) =
N
i=1
log p (xi|q)
=
i
log p (xi = PRI|q) + ...
i
log p (xi = PAN|1 − q)
=nPRI log (q) + (N − nPRI) log (1 − q)
Where nPRI are the numbers of individuals who are planning to vote PRI
this fall 68 / 117

133. We use our classic tricks
By setting
L = log p (X|q) (4)
We have that
∂L
∂q
= 0 (5)
Thus
nPRI
q
−
(N − nPRI)
(1 − q)
= 0 (6)
69 / 117

134. We use our classic tricks
By setting
L = log p (X|q) (4)
We have that
∂L
∂q
= 0 (5)
Thus
nPRI
q
−
(N − nPRI)
(1 − q)
= 0 (6)
69 / 117

135. We use our classic tricks
By setting
L = log p (X|q) (4)
We have that
∂L
∂q
= 0 (5)
Thus
nPRI
q
−
(N − nPRI)
(1 − q)
= 0 (6)
69 / 117

136. Final Solution of ML
We get
qPRI =
nPRI
N
(7)
Thus
If we say that N = 20 and if 12 are going to vote PRI, we get qPRI = 0.6.
70 / 117

137. Final Solution of ML
We get
qPRI =
nPRI
N
(7)
Thus
If we say that N = 20 and if 12 are going to vote PRI, we get qPRI = 0.6.
70 / 117

138. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

139. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

140. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

141. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

142. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

143. Building the MAP estimate
Obviously we need a prior belief distribution
We have the following constraints:
The prior for q must be zero outside the [0, 1] interval.
Within the [0, 1] interval, we are free to specify our beliefs in any way
we wish.
In most cases, we would want to choose a distribution for the prior
beliefs that peaks somewhere in the [0, 1] interval.
We assume the following
The state of Colima has traditionally voted PRI in presidential
elections.
However, on account of the prevailing economic conditions, the voters
are more likely to vote PAN in the election in question.
71 / 117

144. What prior distribution can we use?
We could use a Beta distribution being parametrized by two values α
and β
p (q) =
1
B (α, β)
qα−1
(1 − q)β−1
. (8)
Where
We have B (α, β) = Γ(α)Γ(β)
Γ(α+β) is the beta function where Γ is the
generalization of the notion of factorial in the case of the real numbers.
Properties
When both the α, β > 0 then the beta distribution has its mode
(Maximum value) at
α − 1
α + β − 2
. (9)
72 / 117

145. What prior distribution can we use?
We could use a Beta distribution being parametrized by two values α
and β
p (q) =
1
B (α, β)
qα−1
(1 − q)β−1
. (8)
Where
We have B (α, β) = Γ(α)Γ(β)
Γ(α+β) is the beta function where Γ is the
generalization of the notion of factorial in the case of the real numbers.
Properties
When both the α, β > 0 then the beta distribution has its mode
(Maximum value) at
α − 1
α + β − 2
. (9)
72 / 117

146. What prior distribution can we use?
We could use a Beta distribution being parametrized by two values α
and β
p (q) =
1
B (α, β)
qα−1
(1 − q)β−1
. (8)
Where
We have B (α, β) = Γ(α)Γ(β)
Γ(α+β) is the beta function where Γ is the
generalization of the notion of factorial in the case of the real numbers.
Properties
When both the α, β > 0 then the beta distribution has its mode
(Maximum value) at
α − 1
α + β − 2
. (9)
72 / 117

147. We then do the following
We do the following
We can choose α = β so the beta prior peaks at 0.5.
As a further expression of our belief
We make the following choice α = β = 5.
Why? Look at the variance of the beta distribution
αβ
(α + β)2
(α + β + 1)
. (10)
73 / 117

148. We then do the following
We do the following
We can choose α = β so the beta prior peaks at 0.5.
As a further expression of our belief
We make the following choice α = β = 5.
Why? Look at the variance of the beta distribution
αβ
(α + β)2
(α + β + 1)
. (10)
73 / 117

149. We then do the following
We do the following
We can choose α = β so the beta prior peaks at 0.5.
As a further expression of our belief
We make the following choice α = β = 5.
Why? Look at the variance of the beta distribution
αβ
(α + β)2
(α + β + 1)
. (10)
73 / 117

150. Thus, we have the following nice properties
We have a variance with α = β = 5
V ar (q) ≈ 0.025
Thus, the standard deviation
sd ≈ 0.16 which is a nice dispersion at the peak point!!!
74 / 117

151. Thus, we have the following nice properties
We have a variance with α = β = 5
V ar (q) ≈ 0.025
Thus, the standard deviation
sd ≈ 0.16 which is a nice dispersion at the peak point!!!
74 / 117

152. Now, our MAP estimate for pMAP ...
We have then
pMAP = argmax
Θ


xi∈X
log p (xi|q) + log p (q)

 (11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI) log (1 − q) + log p (q)] (12)
Where
log p (q) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
75 / 117

153. Now, our MAP estimate for pMAP ...
We have then
pMAP = argmax
Θ


xi∈X
log p (xi|q) + log p (q)

 (11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI) log (1 − q) + log p (q)] (12)
Where
log p (q) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
75 / 117

154. Now, our MAP estimate for pMAP ...
We have then
pMAP = argmax
Θ


xi∈X
log p (xi|q) + log p (q)

 (11)
Plugging back the ML
pMAP = argmax
Θ
[nPRI log q + (N − nPRI) log (1 − q) + log p (q)] (12)
Where
log p (q) = log
1
B (α, β)
qα−1
(1 − q)β−1
(13)
75 / 117

155. The log of p (q)
We have that
log p (q) = (α − 1) log q + (β − 1) log (1 − q) − log B (α, β) (14)
Now taking the derivative with respect to q, we get
nPRI
q
−
(N − nPRI)
(1 − q)
−
β − 1
1 − q
+
α − 1
q
= 0 (15)
Thus
qMAP =
nPRI + α − 1
N + α + β − 2
(16)
76 / 117

156. The log of p (q)
We have that
log p (q) = (α − 1) log q + (β − 1) log (1 − q) − log B (α, β) (14)
Now taking the derivative with respect to q, we get
nPRI
q
−
(N − nPRI)
(1 − q)
−
β − 1
1 − q
+
α − 1
q
= 0 (15)
Thus
qMAP =
nPRI + α − 1
N + α + β − 2
(16)
76 / 117

157. The log of p (q)
We have that
log p (q) = (α − 1) log q + (β − 1) log (1 − q) − log B (α, β) (14)
Now taking the derivative with respect to q, we get
nPRI
q
−
(N − nPRI)
(1 − q)
−
β − 1
1 − q
+
α − 1
q
= 0 (15)
Thus
qMAP =
nPRI + α − 1
N + α + β − 2
(16)
76 / 117

158. Now
With N = 20 with nPRI = 12 and α = β = 5
qMAP = 0.571
77 / 117

159. Another Example
Let X1, ..., Xn given θ are Poisson P (θ) with probability
f (xi|θ) = θxi
xi!
e−θ
Assume θ ∼ Γ (α, β) given by π (θ) ∝ θα−1e−βθ
The MAP is equal to
π (θ|X1, X2, ..., Xn) = π θ| Xi ∝ θ Xi+α−1
e−(n+β)θ
Basically Γ ( Xi + α − 1, n + β)
The mean is
E [θ|X] =
Xi + α
n + β
78 / 117

160. Another Example
Let X1, ..., Xn given θ are Poisson P (θ) with probability
f (xi|θ) = θxi
xi!
e−θ
Assume θ ∼ Γ (α, β) given by π (θ) ∝ θα−1e−βθ
The MAP is equal to
π (θ|X1, X2, ..., Xn) = π θ| Xi ∝ θ Xi+α−1
e−(n+β)θ
Basically Γ ( Xi + α − 1, n + β)
The mean is
E [θ|X] =
Xi + α
n + β
78 / 117

161. Another Example
Let X1, ..., Xn given θ are Poisson P (θ) with probability
f (xi|θ) = θxi
xi!
e−θ
Assume θ ∼ Γ (α, β) given by π (θ) ∝ θα−1e−βθ
The MAP is equal to
π (θ|X1, X2, ..., Xn) = π θ| Xi ∝ θ Xi+α−1
e−(n+β)θ
Basically Γ ( Xi + α − 1, n + β)
The mean is
E [θ|X] =
Xi + α
n + β
78 / 117

162. Now, given the mean of the Γ
We can rewrite the mean as
E [θ|X] =
n
n + β
×
Xi
n
+
β
β + n
×
α
β
Given that the means are
Mean of MLE
Xi
n
Mean of the prior α
β
79 / 117

163. Now, given the mean of the Γ
We can rewrite the mean as
E [θ|X] =
n
n + β
×
Xi
n
+
β
β + n
×
α
β
Given that the means are
Mean of MLE
Xi
n
Mean of the prior α
β
79 / 117

164. Remarks
Something Notable
The standard MLE maximizes π (θ|x), while the generalized MLE
maximizes π(θ) (θ).
Quite funny we call that Maximum Aposteriori (MAP) estimator!!!
The MAP estimator is since it is often simpler to calculate given that
arg max
θ
π (θ|x) = arg max
θ
f (x|θ) π (θ)
Given that the normalization factor is a constant
80 / 117

165. Remarks
Something Notable
The standard MLE maximizes π (θ|x), while the generalized MLE
maximizes π(θ) (θ).
Quite funny we call that Maximum Aposteriori (MAP) estimator!!!
The MAP estimator is since it is often simpler to calculate given that
arg max
θ
π (θ|x) = arg max
θ
f (x|θ) π (θ)
Given that the normalization factor is a constant
80 / 117

166. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
81 / 117

167. Properties
First
MAP estimation “pulls” the estimate toward the prior.
Second
The more focused our prior belief, the larger the pull toward the prior.
Example
If α = β =equal to large value
It will make the MAP estimate to move closer to the prior.
82 / 117

168. Properties
First
MAP estimation “pulls” the estimate toward the prior.
Second
The more focused our prior belief, the larger the pull toward the prior.
Example
If α = β =equal to large value
It will make the MAP estimate to move closer to the prior.
82 / 117

169. Properties
First
MAP estimation “pulls” the estimate toward the prior.
Second
The more focused our prior belief, the larger the pull toward the prior.
Example
If α = β =equal to large value
It will make the MAP estimate to move closer to the prior.
82 / 117

170. Properties
Third
In the expression we derived for qMAP , the parameters α and β play a
“smoothing” role vis-a-vis the measurement nPRI.
Fourth
Since we referred to q as the parameter to be estimated, we can refer to α
and β as the hyper-parameters in the estimation calculations.
83 / 117

171. Properties
Third
In the expression we derived for qMAP , the parameters α and β play a
“smoothing” role vis-a-vis the measurement nPRI.
Fourth
Since we referred to q as the parameter to be estimated, we can refer to α
and β as the hyper-parameters in the estimation calculations.
83 / 117

172. Beyond simple derivation
In the previous technique
We took an logarithm of the likelihood × the prior to obtain a function
that can be derived in order to obtain each of the parameters to be
estimated.
What if we cannot derive?
For example when we have something like |θi|.
We can try the following
EM + MAP to be able to estimate the sought parameters.
84 / 117

173. Beyond simple derivation
In the previous technique
We took an logarithm of the likelihood × the prior to obtain a function
that can be derived in order to obtain each of the parameters to be
estimated.
What if we cannot derive?
For example when we have something like |θi|.
We can try the following
EM + MAP to be able to estimate the sought parameters.
84 / 117

174. Beyond simple derivation
In the previous technique
We took an logarithm of the likelihood × the prior to obtain a function
that can be derived in order to obtain each of the parameters to be
estimated.
What if we cannot derive?
For example when we have something like |θi|.
We can try the following
EM + MAP to be able to estimate the sought parameters.
84 / 117

175. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
85 / 117

176. Imagine an action space and a ∈ A
For example
In estimation problems, A is the set of real numbers and a is a
number, say a = 2 is adopted as an estimator of θ ∈ Θ.
Another One
In testing problems, the action space is A = {accept, reject}
86 / 117

177. Imagine an action space and a ∈ A
For example
In estimation problems, A is the set of real numbers and a is a
number, say a = 2 is adopted as an estimator of θ ∈ Θ.
Another One
In testing problems, the action space is A = {accept, reject}
86 / 117

178. Everytime you make a decision you have a Loss
Actually
Statisticians are pessimistic creatures that replaced nicely coined term
utility to a more somber term loss!!!
How do we denote such losses?
A classic one L (θ, a)
representing the payoff by a decision maker (statistician) if he takes
any action a ∈ A in certina state of nature θ
87 / 117

179. Everytime you make a decision you have a Loss
Actually
Statisticians are pessimistic creatures that replaced nicely coined term
utility to a more somber term loss!!!
How do we denote such losses?
A classic one L (θ, a)
representing the payoff by a decision maker (statistician) if he takes
any action a ∈ A in certina state of nature θ
87 / 117

180. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
88 / 117

181. Examples
Squared Error Loss
L (θ, a) = (θ − a)2
Absolute Loss
L (θ, a) = |θ − a|
0-1 Loss example
L (θ, a) = I [|θ − a| > m]
89 / 117

182. Examples
Squared Error Loss
L (θ, a) = (θ − a)2
Absolute Loss
L (θ, a) = |θ − a|
0-1 Loss example
L (θ, a) = I [|θ − a| > m]
89 / 117

183. Examples
Squared Error Loss
L (θ, a) = (θ − a)2
Absolute Loss
L (θ, a) = |θ − a|
0-1 Loss example
L (θ, a) = I [|θ − a| > m]
89 / 117

184. Clearly the easiest mathematically SEL
Additionally, it is linked with
EX|θ [θ − δ (X)]2
= V ar (δ (X)) + [bias (δ (X))]2
Where bias (δ (X)) = EX|θ [δ (X)] − θ
90 / 117

185. In another example
The median, m, of random variable X is defined as
P (X ≥ m) ≥
1
2
,
P (X ≤ m) ≤
1
2
Assuming the absolute loss
ϕ (a) =Eθ|X [|θ − a|]
=
θ≥a
(θ − a) π (θ|X) dθ +
θ≤a
(a − θ) π (θ|X) dθ
=
∞
a
(θ − a) π (θ|X) dθ +
a
∞
(a − θ) π (θ|X) dθ
91 / 117

186. In another example
The median, m, of random variable X is defined as
P (X ≥ m) ≥
1
2
,
P (X ≤ m) ≤
1
2
Assuming the absolute loss
ϕ (a) =Eθ|X [|θ − a|]
=
θ≥a
(θ − a) π (θ|X) dθ +
θ≤a
(a − θ) π (θ|X) dθ
=
∞
a
(θ − a) π (θ|X) dθ +
a
∞
(a − θ) π (θ|X) dθ
91 / 117

187. In another example
The median, m, of random variable X is defined as
P (X ≥ m) ≥
1
2
,
P (X ≤ m) ≤
1
2
Assuming the absolute loss
ϕ (a) =Eθ|X [|θ − a|]
=
θ≥a
(θ − a) π (θ|X) dθ +
θ≤a
(a − θ) π (θ|X) dθ
=
∞
a
(θ − a) π (θ|X) dθ +
a
∞
(a − θ) π (θ|X) dθ
91 / 117

188. In another example
The median, m, of random variable X is defined as
P (X ≥ m) ≥
1
2
,
P (X ≤ m) ≤
1
2
Assuming the absolute loss
ϕ (a) =Eθ|X [|θ − a|]
=
θ≥a
(θ − a) π (θ|X) dθ +
θ≤a
(a − θ) π (θ|X) dθ
=
∞
a
(θ − a) π (θ|X) dθ +
a
∞
(a − θ) π (θ|X) dθ
91 / 117

189. Then
Using the following equivalence
∂
∂x
g(x)
f(x)
φ (x, t) dt =
g(x)
f(x)
∂
∂x
φ (x, t) dt + φ (x, g (x))
∂g (x)
∂x
− ...
φ (x, f (x))
∂f (x)
∂x
Then
∂ϕ (a)
∂a
= −
∞
a
π (θ|X) dθ + 0 − 0 +
a
∞
π (θ|X) dθ + 0 − 0
92 / 117

190. Then
Using the following equivalence
∂
∂x
g(x)
f(x)
φ (x, t) dt =
g(x)
f(x)
∂
∂x
φ (x, t) dt + φ (x, g (x))
∂g (x)
∂x
− ...
φ (x, f (x))
∂f (x)
∂x
Then
∂ϕ (a)
∂a
= −
∞
a
π (θ|X) dθ + 0 − 0 +
a
∞
π (θ|X) dθ + 0 − 0
92 / 117

191. Therefore
We have then
∂ϕ (a)
∂a
= −Pθ|X (θ ≥ a) + Pθ|X (θ ≤ a) = 0
The value of a for which Pθ|X (θ ≥ a) = Pθ|X (θ ≤ a) is the median
Since ∂2ϕ(a)
∂a2 = 2π (a|X) > 0 by the Fundamental theorem of calculus
93 / 117

192. Therefore
We have then
∂ϕ (a)
∂a
= −Pθ|X (θ ≥ a) + Pθ|X (θ ≤ a) = 0
The value of a for which Pθ|X (θ ≥ a) = Pθ|X (θ ≤ a) is the median
Since ∂2ϕ(a)
∂a2 = 2π (a|X) > 0 by the Fundamental theorem of calculus
93 / 117

193. Finally
The Median Minimize
ϕ (a)
94 / 117

194. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
95 / 117

195. Bayesian Expected Loss
Definition
Bayesian expected loss is the expectation of the loss function with
respect to posterior measure,
ρ (a, π) = Eθ|X [L (a, θ)] =
Θ
L (θ, a) π (θ|x) dθ
Here, we have an important principle
Referring to the less possible loss!!!
96 / 117

196. Bayesian Expected Loss
Definition
Bayesian expected loss is the expectation of the loss function with
respect to posterior measure,
ρ (a, π) = Eθ|X [L (a, θ)] =
Θ
L (θ, a) π (θ|x) dθ
Here, we have an important principle
Referring to the less possible loss!!!
96 / 117

197. The Expected Loss Principle
Definition
In comparing two actions a1 = δ1(X) and a2 = δ2(X), after data X
had been observed, preferred action is the one for which the posterior
expected loss is smaller.
Therefore
An action a∗ that minimizes the posterior expected loss is called
Bayes action.
97 / 117

198. The Expected Loss Principle
Definition
In comparing two actions a1 = δ1(X) and a2 = δ2(X), after data X
had been observed, preferred action is the one for which the posterior
expected loss is smaller.
Therefore
An action a∗ that minimizes the posterior expected loss is called
Bayes action.
97 / 117

199. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
98 / 117

200. Example
If the loss is squared error
The Bayes action a∗ is found by minimizing
ϕ (a) = Eθ|X (θ − a)2
= a2
− 2Eθ|X [θ] a + Eθ|Xθ2
Then, we want ϕ (a) = 0
Solving for it, we have a = Eθ|X [θ]
Additionally
ϕ (a) < 0 then a∗ = Eθ|X [θ] is a Bayesian Action.
99 / 117

201. Example
If the loss is squared error
The Bayes action a∗ is found by minimizing
ϕ (a) = Eθ|X (θ − a)2
= a2
− 2Eθ|X [θ] a + Eθ|Xθ2
Then, we want ϕ (a) = 0
Solving for it, we have a = Eθ|X [θ]
Additionally
ϕ (a) < 0 then a∗ = Eθ|X [θ] is a Bayesian Action.
99 / 117

202. Example
If the loss is squared error
The Bayes action a∗ is found by minimizing
ϕ (a) = Eθ|X (θ − a)2
= a2
− 2Eθ|X [θ] a + Eθ|Xθ2
Then, we want ϕ (a) = 0
Solving for it, we have a = Eθ|X [θ]
Additionally
ϕ (a) < 0 then a∗ = Eθ|X [θ] is a Bayesian Action.
99 / 117

203. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
100 / 117

204. Given X ∈ {Pθ, θ ∈ Θ}
A family which is indexed by a parameter (random variable) θ
Here, we change our Bayesian hat to the frequentist one
This allows to make inferences about θ
A solution is a decision procedure (decision rule) δ (x), that identifies
particular inference for each value of x that can be observed.
101 / 117

205. Given X ∈ {Pθ, θ ∈ Θ}
A family which is indexed by a parameter (random variable) θ
Here, we change our Bayesian hat to the frequentist one
This allows to make inferences about θ
A solution is a decision procedure (decision rule) δ (x), that identifies
particular inference for each value of x that can be observed.
101 / 117

206. A be the class of all possible realizations of δ(x), i.e.
actions
The Loss function L (θ, a) maps Θ × A −→ R
Defining a cost to the statistician when he takes the action a and the
true value of the parameter is θ.
Then we can define a decision function called Risk
R (θ, δ) = EX|θ [L (θ|δ (X))] =
X
L (θ|δ (X)) f (x|θ) dx
A frequentist risk on the performance of δ.
102 / 117

207. A be the class of all possible realizations of δ(x), i.e.
actions
The Loss function L (θ, a) maps Θ × A −→ R
Defining a cost to the statistician when he takes the action a and the
true value of the parameter is θ.
Then we can define a decision function called Risk
R (θ, δ) = EX|θ [L (θ|δ (X))] =
X
L (θ|δ (X)) f (x|θ) dx
A frequentist risk on the performance of δ.
102 / 117

208. Therefore
Since the risk function is defined as an average loss with respect to a
sample space
it is called the frequentist risk.
Let D be the collection of all measurable decision rules
There are several ways for assigning the preference among the rules in
D.
103 / 117

209. Therefore
Since the risk function is defined as an average loss with respect to a
sample space
it is called the frequentist risk.
Let D be the collection of all measurable decision rules
There are several ways for assigning the preference among the rules in
D.
103 / 117

210. Furthermore
Some of them are
The Minimax Principle
Γ-minimax Principle
Minimax Principle
etc
The one we are interested is
The Bayes principle
104 / 117

211. Furthermore
Some of them are
The Minimax Principle
Γ-minimax Principle
Minimax Principle
etc
The one we are interested is
The Bayes principle
104 / 117

212. Furthermore
Some of them are
The Minimax Principle
Γ-minimax Principle
Minimax Principle
etc
The one we are interested is
The Bayes principle
104 / 117

213. Furthermore
Some of them are
The Minimax Principle
Γ-minimax Principle
Minimax Principle
etc
The one we are interested is
The Bayes principle
104 / 117

214. Furthermore
Some of them are
The Minimax Principle
Γ-minimax Principle
Minimax Principle
etc
The one we are interested is
The Bayes principle
104 / 117

215. Under the Bayes principle
Bayes risk
r (π, δ) = R (θ, δ) π (dθ) = EθR (θ, δ)
Where there is a δπ , called Bayes rule, minimizing the risk
δπ = arg inf
δ∈D
r (π, δ)
Bayes risk of the prior distribution π (Bayes envelope function) is
r (π) = r (π, δπ)
105 / 117

216. Under the Bayes principle
Bayes risk
r (π, δ) = R (θ, δ) π (dθ) = EθR (θ, δ)
Where there is a δπ , called Bayes rule, minimizing the risk
δπ = arg inf
δ∈D
r (π, δ)
Bayes risk of the prior distribution π (Bayes envelope function) is
r (π) = r (π, δπ)
105 / 117

217. Under the Bayes principle
Bayes risk
r (π, δ) = R (θ, δ) π (dθ) = EθR (θ, δ)
Where there is a δπ , called Bayes rule, minimizing the risk
δπ = arg inf
δ∈D
r (π, δ)
Bayes risk of the prior distribution π (Bayes envelope function) is
r (π) = r (π, δπ)
105 / 117

218. Bayes Envelope Function Definition
Definition
The Bayes Envelope is the maximal reward rate a player could achieve
had he known in advance the relative frequencies of the other players.
In particular, we define the following function as
r (π, δ) = Eθ EX|θ [L (θ, δ (X))]
Therefore the Bayes action as Bayes Rules looks like
δ∗
(x) = arg min
δ∈D
r (π, δ)
106 / 117

219. Bayes Envelope Function Definition
Definition
The Bayes Envelope is the maximal reward rate a player could achieve
had he known in advance the relative frequencies of the other players.
In particular, we define the following function as
r (π, δ) = Eθ EX|θ [L (θ, δ (X))]
Therefore the Bayes action as Bayes Rules looks like
δ∗
(x) = arg min
δ∈D
r (π, δ)
106 / 117

220. Bayes Envelope Function Definition
Definition
The Bayes Envelope is the maximal reward rate a player could achieve
had he known in advance the relative frequencies of the other players.
In particular, we define the following function as
r (π, δ) = Eθ EX|θ [L (θ, δ (X))]
Therefore the Bayes action as Bayes Rules looks like
δ∗
(x) = arg min
δ∈D
r (π, δ)
106 / 117

221. Actually
A classic Bayes Rule
The Naive Bayes Rules for classification using Gaussian’s for
classification
R1 : P (ω1|x) > P (ω2|x)
R2 : P (ω2|x) > P (ω1|x)
107 / 117

222. Outline
1 Introduction
Likelihood Principle
Example, Testing Fairness
Independence Influence
Sufficiency
Fisher-Neyman Characterization
Example
Sufficiency Principle
Conditionality Perspective
Example
Sins of Being non-Bayesian
2 Bayesian Inference
Introduction
Connection with Sufficient Statistics
Generalized Maximum Likelihood Estimator
The Maximum A Posteriori (MAP)
Maximum Likelihood Vs Maximum A Posteriori
Properties of the MAP
3 Loss, Posterior Risk, Bayes Action
Bayes Principle in the Frequentist Decision Theoretic Setup
Examples of Loss Functions
Bayesian Expected Loss Principle
Example
The Empirical Risk
The Fubini’s Theorem
108 / 117

223. The Fubini’s Theorem (Informal Version)
Theorem
Suppose X and Y are σ-finite measure spaces, and suppose that
X × Y is given the product measure:
(µ × ν) (E) = inf



∞
j=1
µ (Aj) ν (Bj) |E ⊂ ∪∞
j=1Aj × Bj



With any non-negative µ × ν-measurable function f, then
X×Y
f (x, y) d (µ × ν) (x, y) =
Y X
f (x, y) dµ (x) dν (y)
109 / 117

224. The Fubini’s Theorem (Informal Version)
Theorem
Suppose X and Y are σ-finite measure spaces, and suppose that
X × Y is given the product measure:
(µ × ν) (E) = inf



∞
j=1
µ (Aj) ν (Bj) |E ⊂ ∪∞
j=1Aj × Bj



With any non-negative µ × ν-measurable function f, then
X×Y
f (x, y) d (µ × ν) (x, y) =
Y X
f (x, y) dµ (x) dν (y)
109 / 117

225. Implications with the Expected Value
We have by the Fubini’s Theorem
r (π, δ) = Eθ EX|θ [L (θ, δ (X))]
= EX Eθ|X [L (θ, δ (X))]
Where the posterior expected loss
ρ (π, δ) = Eθ|X [L (θ, δ (X))]
110 / 117

226. Implications with the Expected Value
We have by the Fubini’s Theorem
r (π, δ) = Eθ EX|θ [L (θ, δ (X))]
= EX Eθ|X [L (θ, δ (X))]
Where the posterior expected loss
ρ (π, δ) = Eθ|X [L (θ, δ (X))]
110 / 117

227. Therefore
r (π, δ) is minimized for any fixed x
When ρ (π, δ) is minimized, for any fixed x, δB (x) = a∗ (x) where *
represent the optimal action.
Basically
This result links the conditional Bayesian and decision theoretic
frequentist inference:
The frequentist Bayes rule conditional on X is the Bayes action.
111 / 117

228. Therefore
r (π, δ) is minimized for any fixed x
When ρ (π, δ) is minimized, for any fixed x, δB (x) = a∗ (x) where *
represent the optimal action.
Basically
This result links the conditional Bayesian and decision theoretic
frequentist inference:
The frequentist Bayes rule conditional on X is the Bayes action.
111 / 117

229. What happens when we have the Squared Loss?
The Bayes rule is the posterior expectation
δB (x) = Θ θf (x|θ) π (θ) dθ
Θ f (x|θ) π (θ) dθ
Not only that, in the case of
L (θ, a) = w (θ) (θ − a)2
112 / 117

230. What happens when we have the Squared Loss?
The Bayes rule is the posterior expectation
δB (x) = Θ θf (x|θ) π (θ) dθ
Θ f (x|θ) π (θ) dθ
Not only that, in the case of
L (θ, a) = w (θ) (θ − a)2
112 / 117

231. We have
The following Bayes Rule
δB (x) = Θ w (θ) θf (x|θ) π (θ) dθ
Θ w (θ) f (x|θ) π (θ) dθ
113 / 117

232. Furthermore
According to a Bayes principle
A rule δ1 (X) is preferred to δ2 (X) if r (π, δ1) < r (π, δ2)
The frequentists use Bayes principle
to compare frequentist risks of the rules R (θ, δ1) and R (θ, δ2).
114 / 117

233. Furthermore
According to a Bayes principle
A rule δ1 (X) is preferred to δ2 (X) if r (π, δ1) < r (π, δ2)
The frequentists use Bayes principle
to compare frequentist risks of the rules R (θ, δ1) and R (θ, δ2).
114 / 117

234. Analysis of frequentist risk
It leads to various concepts as
1 minimaxity,
2 admissibility,
3 unbiasedness,
4 equivariance,
5 etc.
115 / 117

235. D. V. Lindley and L. D. Phillips, “Inference for a bernoulli process (a
bayesian view),” The American Statistician, vol. 30, no. 3,
pp. 112–119, 1976.
C. Aschwanden, “Not even scientists can easily explain p-values.”
https://fivethirtyeight.com/features/not-even-scientists-can-easily-
explain-p-values.
Online; accessed 24 Noviembre 2015.
K. P. F.R.S., “X. on the criterion that a given system of deviations
from the probable in the case of a correlated system of variables is
such that it can be reasonably supposed to have arisen from random
sampling,” The London, Edinburgh, and Dublin Philosophical
Magazine and Journal of Science, vol. 50, no. 302, pp. 157–175, 1900.
116 / 117

236. P. Bickel and K. Doksum, Mathematical Statistics: Basic Ideas and
Selected Topics.
No. v. 1 in Mathematical Statistics: Basic Ideas and Selected Topics,
Prentice Hall, 2001.
R. A. Fisher, “On the mathematical foundations of theoretical
statistics,” Philosophical Transactions of the Royal Society of London.
Series A, Containing Papers of a Mathematical or Physical Character,
vol. 222, no. 594-604, pp. 309–368, 1922.
G. Casella and R. L. Berger, Statistical inference, vol. 2.
Duxbury Pacific Grove, CA, 2002.
S. M. Kay, Fundamentals of statistical signal processing.
Prentice Hall PTR, 1993.
117 / 117