Mohammed Ahmed, profile picture
Uploaded byMohammed Ahmed
PPTX, PDF2,497 views

statics

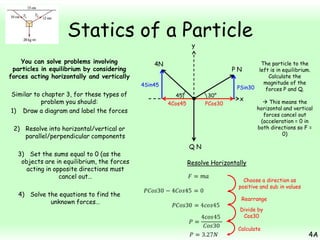
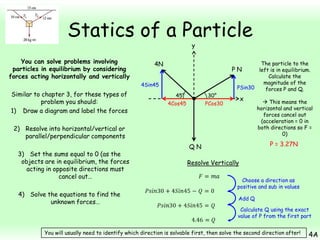
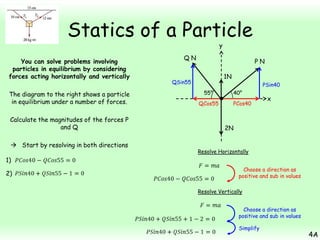
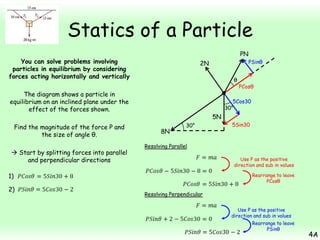
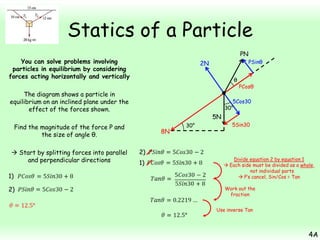
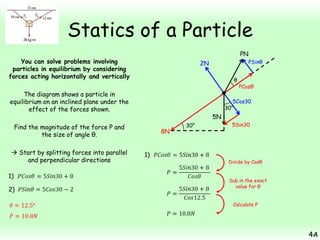
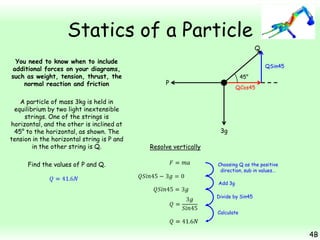
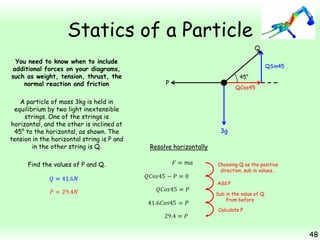
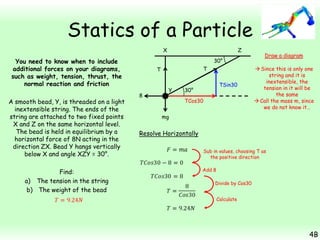
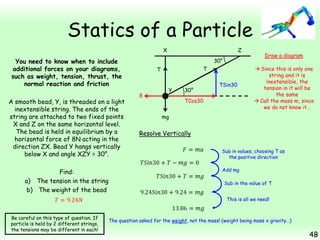
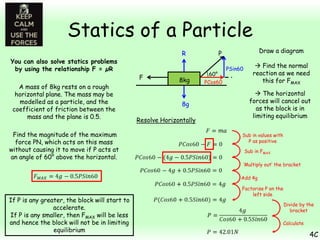
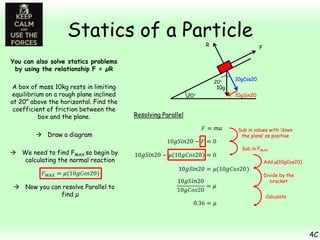
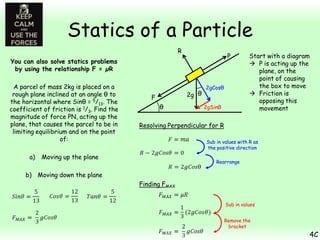
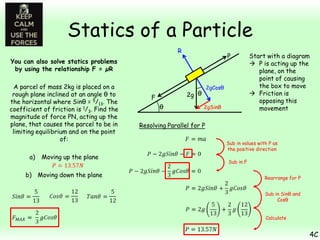
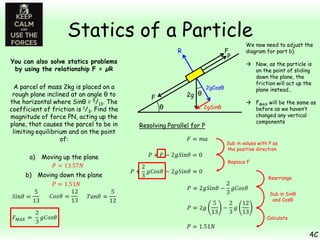
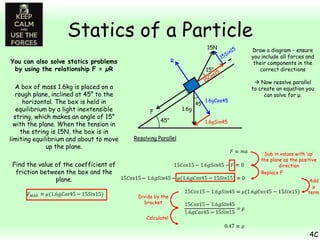
This chapter focuses on objects in static equilibrium, where the net force and net torque on the object are both zero. Solving static equilibrium problems involves drawing free body diagrams showing all external forces acting on the object, then resolving forces into components and setting the sums of forces in each direction equal to zero. Three examples are given of solving static equilibrium problems involving particles under the influence of multiple forces. The problems are solved by resolving forces into horizontal and vertical or parallel and perpendicular components, setting the component force equations equal to zero, and solving the equations to determine the magnitudes of unknown forces. Key steps include drawing diagrams, resolving forces, setting force sums to zero, and solving the resulting equations.

Embed presentation

Downloaded 80 times
Introduction • This chapter builds on chapter 3 and focuses on objects in equilibrium, ie) On the point of moving but actually remaining stationary • As in chapter 3 it involves resolving forces in different directions • Statics is important in engineering for calculating whether structures are stable
Statics of a Particle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically 4N 4Sin45 Similar to chapter 3, for these types of problem you should: 1) Draw a diagram and label the forces 45° 4Cos45 30° PCos30 The particle to the PN left is in equilibrium. Calculate the magnitude of the PSin30 forces P and Q. x 2) Resolve into horizontal/vertical or parallel/perpendicular components 3) Set the sums equal to 0 (as the objects are in equilibrium, the forces acting in opposite directions must cancel out… 4) Solve the equations to find the unknown forces…  This means the horizontal and vertical forces cancel out (acceleration = 0 in both directions so F = 0) QN Resolve Horizontally Choose a direction as positive and sub in values Rearrange Divide by Cos30 Calculate 4A
Statics of a Particle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically 4N 4Sin45 Similar to chapter 3, for these types of problem you should: 1) Draw a diagram and label the forces 45° 4Cos45 30° PCos30 The particle to the PN left is in equilibrium. Calculate the magnitude of the PSin30 forces P and Q. x 2) Resolve into horizontal/vertical or parallel/perpendicular components 3) Set the sums equal to 0 (as the objects are in equilibrium, the forces acting in opposite directions must cancel out… 4) Solve the equations to find the unknown forces…  This means the horizontal and vertical forces cancel out (acceleration = 0 in both directions so F = 0) P = 3.27N QN Resolve Vertically Choose a direction as positive and sub in values Add Q Calculate Q using the exact value of P from the first part You will usually need to identify which direction is solvable first, then solve the second direction after! 4A
Statics of a Particle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically The diagram to the right shows a particle in equilibrium under a number of forces. Calculate the magnitudes of the forces P and Q  Start by resolving in both directions QN PN 1N QSin55 PSin40 55° QCos55 40° PCos40 x 2N Resolve Horizontally 1) 2) Choose a direction as positive and sub in values Resolve Vertically Choose a direction as positive and sub in values Simplify 4A
Statics of a Particle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically QN PN 1N QSin55 PSin40 55° The diagram to the right shows a particle in equilibrium under a number of forces. QCos55 Calculate the magnitudes of the forces P and Q  Start by resolving in both directions 40° PCos40 x 2N 2) Replace P with the Q equivalent 1) Multiply all terms by Cos40 2) Add Cos40  You can now solve these by rearranging one and subbing it into the other! Divide by  Q = 0.769N the bracket Factorise Q on the left side Calculate 4A
Statics of a Particle y QN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically PN 1N QSin55 PSin40 55° The diagram to the right shows a particle in equilibrium under a number of forces. QCos55 Calculate the magnitudes of the forces P and Q 40° PCos40 x 2N  Start by resolving in both directions 1) 1) Sub in Q (use the exact value) 2)  You can now solve these by rearranging one and subbing it into the other!  Q = 0.769N  P = 0.576N Calculate 4A
Statics of a Particle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PCosθ 5Cos30 30° 5N 8N 30° 5Sin30 Resolving Parallel Use P as the positive direction and sub in values 1) 2) PSinθ 2N Rearrange to leave PCosθ Resolving Perpendicular Use P as the positive direction and sub in values Rearrange to leave PSinθ 4A
Statics of a Particle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. 1) 2) PCosθ 5Cos30 30° 5N Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PSinθ 2N 8N 2) 1) 30° 5Sin30 Divide equation 2 by equation 1  Each side must be divided as a whole, not individual parts  P’s cancel, Sin/Cos = Tan Work out the fraction Use inverse Tan 4A
Statics of a Particle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. 1) 2) PCosθ 5Cos30 30° 5N Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PSinθ 2N 8N 1) 30° 5Sin30 Divide by Cosθ Sub in the exact value for θ Calculate P 4A
Statics of a Particle Q You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A particle of mass 3kg is held in equilibrium by two light inextensible strings. One of the strings is horizontal, and the other is inclined at 45° to the horizontal, as shown. The tension in the horizontal string is P and in the other string is Q. Find the values of P and Q. QSin45 45° P QCos45 3g Resolve vertically Choosing Q as the positive direction, sub in values… Add 3g Divide by Sin45 Calculate 4B
Statics of a Particle Q You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A particle of mass 3kg is held in equilibrium by two light inextensible strings. One of the strings is horizontal, and the other is inclined at 45° to the horizontal, as shown. The tension in the horizontal string is P and in the other string is Q. Find the values of P and Q. QSin45 45° P QCos45 3g Resolve horizontally Choosing Q as the positive direction, sub in values… Add P Sub in the value of Q from before Calculate P 4B
Statics of a Particle X You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A smooth bead, Y, is threaded on a light inextensible string. The ends of the string are attached to two fixed points X and Z on the same horizontal level. The bead is held in equilibrium by a horizontal force of 8N acting in the direction ZX. Bead Y hangs vertically below X and angle XZY = 30°. Find: a) The tension in the string b) The weight of the bead Z 30° T T 8 Y TSin30 30° TCos30 Draw a diagram  Since this is only one string and it is inextensible, the tension in it will be the same  Call the mass m, since we do not know it… mg Resolve Horizontally Sub in values, choosing T as the positive direction Add 8 Divide by Cos30 Calculate 4B
Statics of a Particle X You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A smooth bead, Y, is threaded on a light inextensible string. The ends of the string are attached to two fixed points X and Z on the same horizontal level. The bead is held in equilibrium by a horizontal force of 8N acting in the direction ZX. Bead Y hangs vertically below X and angle XZY = 30°. Find: a) The tension in the string b) The weight of the bead Z 30° T T 8 Y 30° TSin30 TCos30 Draw a diagram  Since this is only one string and it is inextensible, the tension in it will be the same  Call the mass m, since we do not know it… mg Resolve Vertically Sub in values, choosing T as the positive direction Add mg Sub in the value of T This is all we need! Be careful on this type of question. If particle is held by 2 different strings, the tensions may be different in each! The question asked for the weight, not the mass! (weight being mass x gravity…) 4B
Statics of a Particle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. Calculate: a) The tension in AC b) The tension in BC A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60  The strings are separate so use T1 and T2 as the tensions 10g Resolving Horizontally Sub in values, choosing T2 as the positive direction Add T1Cos30 Divide by Cos60 4B
Statics of a Particle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60 Resolving Vertically  The strings are separate so use T1 and T2 as the tensions 10g Sub in values, choosing T2 as the positive direction Replace T2 with the expression involving T1 Calculate: a) The tension in AC b) The tension in BC Multiply all terms by Cos60 Add 10gCos60 and factorise left side Divide by the bracket Calculate! 4B
Statics of a Particle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. Calculate: a) The tension in AC b) The tension in BC A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60  The strings are separate so use T1 and T2 as the tensions 10g Find T2 by using the original equation… Sub in the value of T1 Calculate! 4B
Statics of a Particle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. 9.8N T T 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Find the tension using the 1kg mass Resolve in the direction of T and sub in values Add 1g By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 4B
Statics of a Particle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 9.8N 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Resolve Parallel to find P Choose P as the positive direction and sub in values Rearrange Divide by Cos45 Calculate 4B
Statics of a Particle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. 9.8N 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Resolve Perpendicular to find R Choose R as the positive direction and sub in values Rearrange Calculate By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 4B
Statics of a Particle You can also solve statics problems by using the relationship F = µR We have seen before that FMAX is the maximum frictional force possible between two surfaces, and that it will resist any force up to this amount Remember that the frictional force can be lower than this and still prevent movement In statics, FMAX is reached when a body is in limiting equilibrium, ie) on the point of moving A block of mass 3kg rests on a rough horizontal plane. The coefficient of friction between the block and the plane is 0.4. When a horizontal force PN is applied to the block, the block remains in equilibrium. a) Find the value for P for which the equilibrium is limiting b) Find the value of F when P = 8N 3g R F 3kg Resolve vertically for R 3g P Find FMAX Sub in values with R as positive Sub in values It is important to consider which Add 3g Calculate direction the object is about to move as this affects the direction the friction is acting… So if P = 11.76N, then the block is in limiting equilibrium on the point of moving For part b), if P = 8N then equilibrium is not limiting, and P will be matched by a frictional force of 8N 4C
Statics of a Particle You can also solve statics problems by using the relationship F = µR A mass of 8kg rests on a rough horizontal plane. The mass may be modelled as a particle, and the coefficient of friction between the mass and the plane is 0.5. R F 8kg Draw a diagram P 60° PCos60 PSin60  Find the normal reaction as we need this for FMAX 8g Resolve Vertically Find the magnitude of the maximum force PN, which acts on this mass without causing it to move if P acts at an angle of 60° above the horizontal. Sub in values with R as positive Rearrange to find R in terms of P Find FMAX Sub in values Multiply bracket out 4C
Statics of a Particle You can also solve statics problems by using the relationship F = µR A mass of 8kg rests on a rough horizontal plane. The mass may be modelled as a particle, and the coefficient of friction between the mass and the plane is 0.5. Find the magnitude of the maximum force PN, which acts on this mass without causing it to move if P acts at an angle of 60° above the horizontal. R F 8kg 8g Resolve Horizontally Draw a diagram P 60° PCos60 PSin60  Find the normal reaction as we need this for FMAX  The horizontal forces will cancel out as the block is in limiting equilibrium Sub in values with P as positive Sub in FMAX ‘Multiply out’ the bracket Add 4g If P is any greater, the block will start to accelerate. If P is any smaller, then FMAX will be less and hence the block will not be in limiting equilibrium Factorise P on the left side Divide by the bracket Calculate 4C
Statics of a Particle R F You can also solve statics problems by using the relationship F = µR A box of mass 10kg rests in limiting equilibrium on a rough plane inclined at 20° above the horizontal. Find the coefficient of friction between the box and the plane. 10gCos20 10g 10gSin20 Resolving Perpendicular Sub in values with R as positive  Draw a diagram Rearrange  We need to find FMAX so begin by calculating the normal reaction Finding FMAX Sub in R and leave µ 4C
Statics of a Particle R F You can also solve statics problems by using the relationship F = µR A box of mass 10kg rests in limiting equilibrium on a rough plane inclined at 20° above the horizontal. Find the coefficient of friction between the box and the plane.  Draw a diagram  We need to find FMAX so begin by calculating the normal reaction  Now you can resolve Parallel to find µ 10gCos20 10g 10gSin20 Resolving Parallel Sub in values with ‘down the plane’ as positive Sub in FMAX Add µ(10gCos20) Divide by the bracket Calculate 4C
Statics of a Particle You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane Find the other trig ratios – this will be useful later! Hyp 13 5 Opp θ 12 Adj So the opposite side is 5 and the hypotenuse is 13  Use Pythagoras to find the missing side!  Now you can work out the other 2 trig ratio… 4C
Statics of a Particle R P You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) 2g θ F θ 2gCosθ 2gSinθ Start with a diagram  P is acting up the plane, on the point of causing the box to move  Friction is opposing this movement Resolving Perpendicular for R Sub in values with R as the positive direction Moving up the plane Rearrange b) Moving down the plane Finding FMAX Sub in values Remove the bracket 4C
Statics of a Particle R P You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2gCosθ 2g θ F θ 2gSinθ Start with a diagram  P is acting up the plane, on the point of causing the box to move  Friction is opposing this movement Resolving Parallel for P Sub in values with P as the positive direction Sub in F Rearrange for P Sub in Sinθ and Cosθ Calculate 4C
Statics of a Particle F P R You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2gCosθ 2g θ F θ 2gSinθ Resolving Parallel for P We now need to adjust the diagram for part b)  Now, as the particle is on the point of sliding down the plane, the friction will act up the plane instead…  FMAX will be the same as before as we haven’t changed any vertical components Sub in values with P as the positive direction Replace F Rearrange Sub in Sinθ and Cosθ Calculate 4C
Statics of a Particle F P R You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2g θ θ 2gCosθ 2gSinθ We now need to adjust the diagram for part b)  Now, as the particle is on the point of sliding down the plane, the friction will act up the plane instead…  FMAX will be the same as before as we haven’t changed any vertical components A force of 13.57N up the plane is enough to bring the parcel to the point of moving in that direction. Any more will overcome the combination of gravity and friction and the parcel will start moving up A force of 1.51N up the plane is enough, when combined with friction, to prevent the parcel from slipping down the plane and hold it in place. Any less and the parcel will start moving down. 4C
Statics of a Particle 15N You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. Draw a diagram – ensure you include all forces and their components in the correct directions R 15° 1.6g F 45° 45° 1.6gCos45 1.6gSin45  The box is on the point of moving up, so friction is acting down the plane  Find the normal reaction and use it to find FMAX Resolving Perpendicular Sub in values with R as the positive direction Find the value of the coefficient of friction between the box and the plane. Rearrange Finding FMAX Sub in values 4C
Statics of a Particle 15N You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. R 15° 1.6g F 45° 45° 1.6gCos45 Draw a diagram – ensure you include all forces and their components in the correct directions  Now resolve parallel to create an equation you can solve for μ. 1.6gSin45 Resolving Parallel Sub in values with ‘up’ the plane as the positive direction Replace F Find the value of the coefficient of friction between the box and the plane. Divide by the bracket Add μ term Calculate! 4C
Statics of a Particle 10N 15N 15° You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane.  Calculate the new FMAX, first finding the new R… R 1.6g F 45° 45° 1.6gCos45 1.6gSin45 Resolving Perpendicular Sub in values with R as the positive direction Find the value of the coefficient of friction between the box and the plane.  The tension is reduced to 10N. Determine the magnitude and direction of the frictional force in this case Update the diagram (or re-draw it!) Rearrange Finding FMAX Sub in values Calculate 4C
Statics of a Particle 10N 15° You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. Find the value of the coefficient of friction between the box and the plane.  The tension is reduced to 10N. Determine the magnitude and direction of the frictional force in this case Update the diagram (or re-draw it!)  Calculate the new FMAX, first finding the new R… R 1.6g F 45° 45° 1.6gCos45 1.6gSin45  Add up the forces acting parallel to the plane (ignoring friction for now) Resolving Parallel (without friction) The force up the plane will be given by: As this is negative, then without friction, there is an overall force of 1.428N acting down the plane  Therefore, friction will oppose this by acting up the plane  As FMAX = 4.012N, the box will not move and is not in limiting equilibrium 4C
Summary • We have learnt about resolving forces when a particle is in limiting equilibrium • We have seen when and how to include additional forces such as tension and friction • We have looked at situations where friction acts in different directions

More Related Content

PPT
Free body diagram
byChandresh Suthar
 
PPTX
Moment of inertia
byসাফকাত অরিন
 
PPT
Moment of inertia
byUsman Sajid
 
PDF
Unit 1. force system, solved problems on force system.pdf
byVrushali Nalawade
 
PPT
Free body diagrams
byTekZeno
 
PDF
Engineering Mechanics Pdf
byEkeeda
 
PPSX
Basics and statics of particles unit i - GE6253 PPT
byTHANGA KASI RAJAN S
 
PDF
engineering statics :equilibrium
bymusadoto
 
Free body diagram
byChandresh Suthar
 
Moment of inertia
byসাফকাত অরিন
 
Moment of inertia
byUsman Sajid
 
Unit 1. force system, solved problems on force system.pdf
byVrushali Nalawade
 
Free body diagrams
byTekZeno
 
Engineering Mechanics Pdf
byEkeeda
 
Basics and statics of particles unit i - GE6253 PPT
byTHANGA KASI RAJAN S
 
engineering statics :equilibrium
bymusadoto
 

What's hot

PPTX
Unit 5 rigid body dynamics
byTHANGA KASI RAJAN S
 
PPTX
Rigid body equilibrium
byTaral Soliya
 
PDF
Chapter 2
bykrishn_desai
 
PPTX
Lecture 1 Introduction to statics Engineering Mechanics hibbeler 14th edition
byAhmed Mohamed Hassan (Baasaay)
 
PPTX
Equilibrium
byNestor Enriquez
 
PPTX
Diploma i em u iv centre of gravity & moment of inertia
byRai University
 
PPTX
Lecture notes on trusses
byPUP Lopez College of Civil Engg.
 
PDF
Engineering Mechanics 1st Year
byEkeeda
 
PDF
6161103 10.9 mass moment of inertia
byetcenterrbru
 
PDF
Lesson 04, shearing force and bending moment 01
byMsheer Bargaray
 
DOCX
ROTATION OF RIGID BODIES
byshahzadebaujiti
 
PPT
Engineering Mechanics Ch 1 Force System.ppt
byVrushali Nalawade
 
PPT
Resultant of forces
byHUSSAIN SHAIK
 
PDF
Relative velocity method, velocity & acceleration analysis of mechanism
byKESHAV
 
PDF
Engineering Mechanics
byKrishna Chaitanya Mummareddy
 
PPT
moments couples and force couple systems by ahmad khan
bySelf-employed
 
PPTX
LAWS FOR THE RESULTANT FORCE
byMr.Ramesh Chandra Panda
 
PPT
Free body diagram Concept in Mechanics
byphysicscatalyst
 
PPTX
Lami's Theorem | Mechanical Engineering
byTransweb Global Inc
 
PPT
Moment
bymuniryaseen
 
Unit 5 rigid body dynamics
byTHANGA KASI RAJAN S
 
Rigid body equilibrium
byTaral Soliya
 
Chapter 2
bykrishn_desai
 
Lecture 1 Introduction to statics Engineering Mechanics hibbeler 14th edition
byAhmed Mohamed Hassan (Baasaay)
 
Equilibrium
byNestor Enriquez
 
Diploma i em u iv centre of gravity & moment of inertia
byRai University
 
Lecture notes on trusses
byPUP Lopez College of Civil Engg.
 
Engineering Mechanics 1st Year
byEkeeda
 
6161103 10.9 mass moment of inertia
byetcenterrbru
 
Lesson 04, shearing force and bending moment 01
byMsheer Bargaray
 
ROTATION OF RIGID BODIES
byshahzadebaujiti
 
Engineering Mechanics Ch 1 Force System.ppt
byVrushali Nalawade
 
Resultant of forces
byHUSSAIN SHAIK
 
Relative velocity method, velocity & acceleration analysis of mechanism
byKESHAV
 
Engineering Mechanics
byKrishna Chaitanya Mummareddy
 
moments couples and force couple systems by ahmad khan
bySelf-employed
 
LAWS FOR THE RESULTANT FORCE
byMr.Ramesh Chandra Panda
 
Free body diagram Concept in Mechanics
byphysicscatalyst
 
Lami's Theorem | Mechanical Engineering
byTransweb Global Inc
 
Moment
bymuniryaseen
 

Viewers also liked

PPT
Basic Principles of Statics
byUTM International Campus
 
PPT
Statics
byRamasubbu .P
 
PDF
Static Equilibrium, Reactions, and Supports
byMohammad Tawfik
 
PPT
Chapter4: Statics - Torques and equilibrium
bySaid Azar
 
PPS
Statics free body diagram
byGourav Kapoor
 
PPT
Static equilibrium chartres
byNikki Ting
 
PPT
Chap1 open channel flow
byUTM International Campus
 
PPTX
Introduction of system of coplanar forces (engineering mechanics)
bymashnil Gaddapawar
 
PPT
Structures and Materials- Section 5 Major Structural Materials for Aeronautic...
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPT
Structures and Materials- Outline and Introduction
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPT
Structures and Materials- Section 2 Tension
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPT
Structures and Materials- Section 6 Axially Loaded Structural Members
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPT
Structures and Materials- Section 3 Stress-Strain Relationships
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPT
truses and frame
byUnikl MIMET
 
PPT
Structures and Materials- Section 1 Statics
byThe Engineering Centre for Excellence in Teaching and Learning
 
PDF
Dymanics of open channel flow
byMohsin Siddique
 
PPT
Structures and Materials- Section 4 Behaviour of Materials
byThe Engineering Centre for Excellence in Teaching and Learning
 
PPTX
FORCE, TYPES, & SYSTEM OF FORCES
byManish Jha
 
PPT
Structures and Materials- Section 7 Stress Concentration
byThe Engineering Centre for Excellence in Teaching and Learning
 
DOC
Yearly scheme of work physics lower 6 2010
bymasyati
 
Basic Principles of Statics
byUTM International Campus
 
Statics
byRamasubbu .P
 
Static Equilibrium, Reactions, and Supports
byMohammad Tawfik
 
Chapter4: Statics - Torques and equilibrium
bySaid Azar
 
Statics free body diagram
byGourav Kapoor
 
Static equilibrium chartres
byNikki Ting
 
Chap1 open channel flow
byUTM International Campus
 
Introduction of system of coplanar forces (engineering mechanics)
bymashnil Gaddapawar
 
Structures and Materials- Section 5 Major Structural Materials for Aeronautic...
byThe Engineering Centre for Excellence in Teaching and Learning
 
Structures and Materials- Outline and Introduction
byThe Engineering Centre for Excellence in Teaching and Learning
 
Structures and Materials- Section 2 Tension
byThe Engineering Centre for Excellence in Teaching and Learning
 
Structures and Materials- Section 6 Axially Loaded Structural Members
byThe Engineering Centre for Excellence in Teaching and Learning
 
Structures and Materials- Section 3 Stress-Strain Relationships
byThe Engineering Centre for Excellence in Teaching and Learning
 
truses and frame
byUnikl MIMET
 
Structures and Materials- Section 1 Statics
byThe Engineering Centre for Excellence in Teaching and Learning
 
Dymanics of open channel flow
byMohsin Siddique
 
Structures and Materials- Section 4 Behaviour of Materials
byThe Engineering Centre for Excellence in Teaching and Learning
 
FORCE, TYPES, & SYSTEM OF FORCES
byManish Jha
 
Structures and Materials- Section 7 Stress Concentration
byThe Engineering Centre for Excellence in Teaching and Learning
 
Yearly scheme of work physics lower 6 2010
bymasyati
 

Similar to statics

PPTX
Chapter_3.pptx statics presentation asdf
byjwinterm1
 
PDF
Chapter 3
byhomari95
 
PPTX
Ch 3 section 3.1-3.3 statics class notes.pptx
byangelramirez121317
 
PPT
Ch3
byjakeharo23
 
PPTX
Static_Equilibrium_Lecture_Summary.pptx physicsphysicsphysicsphysicsphysicsph...
byNursultanDoman3
 
PPT
chapter1and2.ppt
byRanaUmair74
 
PDF
Statics
byRadwaSalehh
 
PDF
Lecture slide on Equilibrium of a Particle.pdf
byKhums Musopa
 
PDF
Lect 4_Statics Dr. ALI AL-SHATRI Che. Eng. .pdf
byAbu Hussein
 
PPT
intro.ppt
byanbh30
 
PPTX
Ch 3 section 3.4 class notes statics .pptx
byangelramirez121317
 
PPS
Equilibrium
bywallflower018
 
PDF
1741095719_KESETIMBANGAN PARTIKEL.1323354
bycandrakrisna595
 
PPTX
Lecture statistics categories glcs 1.pptx
bymahmoud836883
 
PPTX
Mechanic Machine
byMalaysia
 
PPT
3.Chapter 3.ppt equilibrium of a particle
byFarnazBatool2
 
PPTX
Equilibrium
byAHMED SABER
 
PPTX
project statics
byAhmed bssam
 
PDF
EM-(ME)-LECTURE NOTES-R18_08-08-2019Final_compressed.pdf
bygiri yadav swamy
 
PPTX
ENGG MECHANICS-2.pptx Engineering Mechanics - Statics
byManojTharian
 
Chapter_3.pptx statics presentation asdf
byjwinterm1
 
Chapter 3
byhomari95
 
Ch 3 section 3.1-3.3 statics class notes.pptx
byangelramirez121317
 
Ch3
byjakeharo23
 
Static_Equilibrium_Lecture_Summary.pptx physicsphysicsphysicsphysicsphysicsph...
byNursultanDoman3
 
chapter1and2.ppt
byRanaUmair74
 
Statics
byRadwaSalehh
 
Lecture slide on Equilibrium of a Particle.pdf
byKhums Musopa
 
Lect 4_Statics Dr. ALI AL-SHATRI Che. Eng. .pdf
byAbu Hussein
 
intro.ppt
byanbh30
 
Ch 3 section 3.4 class notes statics .pptx
byangelramirez121317
 
Equilibrium
bywallflower018
 
1741095719_KESETIMBANGAN PARTIKEL.1323354
bycandrakrisna595
 
Lecture statistics categories glcs 1.pptx
bymahmoud836883
 
Mechanic Machine
byMalaysia
 
3.Chapter 3.ppt equilibrium of a particle
byFarnazBatool2
 
Equilibrium
byAHMED SABER
 
project statics
byAhmed bssam
 
EM-(ME)-LECTURE NOTES-R18_08-08-2019Final_compressed.pdf
bygiri yadav swamy
 
ENGG MECHANICS-2.pptx Engineering Mechanics - Statics
byManojTharian
 

More from Mohammed Ahmed

PDF
dynamics text (M1)
byMohammed Ahmed
 
PDF
C3 bronze 1
byMohammed Ahmed
 
PPTX
vectors
byMohammed Ahmed
 
PPTX
vectors
byMohammed Ahmed
 
PDF
Simltaneous equations
byMohammed Ahmed
 
PPTX
Moments
byMohammed Ahmed
 
PPTX
Dynamics (full chapter)
byMohammed Ahmed
 
PPT
Chap 3 3a to 3d
byMohammed Ahmed
 
PPT
Kinematics displacement velocity graphs
byMohammed Ahmed
 
PDF
Kinematics
byMohammed Ahmed
 
PPTX
Kinematics jan 27
byMohammed Ahmed
 
PPT
C2 differentiation jan 22
byMohammed Ahmed
 
PPT
Differentiation jan 21, 2014
byMohammed Ahmed
 
PPS
Trigonometric Functions and their Graphs
byMohammed Ahmed
 
dynamics text (M1)
byMohammed Ahmed
 
C3 bronze 1
byMohammed Ahmed
 
vectors
byMohammed Ahmed
 
vectors
byMohammed Ahmed
 
Simltaneous equations
byMohammed Ahmed
 
Moments
byMohammed Ahmed
 
Dynamics (full chapter)
byMohammed Ahmed
 
Chap 3 3a to 3d
byMohammed Ahmed
 
Kinematics displacement velocity graphs
byMohammed Ahmed
 
Kinematics
byMohammed Ahmed
 
Kinematics jan 27
byMohammed Ahmed
 
C2 differentiation jan 22
byMohammed Ahmed
 
Differentiation jan 21, 2014
byMohammed Ahmed
 
Trigonometric Functions and their Graphs
byMohammed Ahmed
 

Recently uploaded

PDF
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PPTX
PRE TERM LABOR ( PREMATURE LABOUR IN PREGNANCY)
byMuthu Kumar
 
PPTX
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
PDF
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
PPTX
Greengnorance Toolkit Module 4 Active Mobility and Transport
byKarl Donert
 
PDF
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
PPTX
Plato's Insight model teaching and learning.pptx
byNikhitaDS
 
PDF
The Sheep and the Goat: Beckett’s Subversion of Divine Justice in Waiting for...
bysejadchokiya
 
PPTX
Q4_PPT MUSIC & ARTS 7 week 1-2, matatag curriculum
byZEN
 
PPTX
Math 8 Quarter 4 Week 3 PRIMARY DATA.pptx
byshahanieabbat3
 
PDF
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
PPTX
Types of counselling Directive, Non Directive, Eclectic Counselling
byPriya Sush
 
PDF
PHARMACOLOGY 1 ( BP 404 T) Unit 1 (Cology 1)
byChetan Mali
 
PPTX
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
PDF
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
PDF
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
PDF
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
PDF
Nursing care plan for Vomiting /B.Sc nsg
byDr. Sudhadevi Sadanandan
 
PDF
Holm Community Heritage at St Nicholas Kirk - 2025 AGM Minutes (30.04.2025)
byAntoine Pietri
 
PPTX
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 
Family and Marriage __ Sociology __ Jhasketan Kuanar __ NURSING VIBE ONLY .pdf
byJK NURSING VIBES ONLY JHASKETAN KUANAR
 
PRE TERM LABOR ( PREMATURE LABOUR IN PREGNANCY)
byMuthu Kumar
 
How to Create_Generate Engineering Change Orders ECOs in Odoo 18
byCeline George
 
Pharmaceutical Quality Assurance Unit 1 (BP606T)
byChetan Mali
 
Greengnorance Toolkit Module 4 Active Mobility and Transport
byKarl Donert
 
Workshop 29 Crystal Review All Students by YogiGoddess
by©LDMMIA, ©Reiki Yoga
 
Plato's Insight model teaching and learning.pptx
byNikhitaDS
 
The Sheep and the Goat: Beckett’s Subversion of Divine Justice in Waiting for...
bysejadchokiya
 
Q4_PPT MUSIC & ARTS 7 week 1-2, matatag curriculum
byZEN
 
Math 8 Quarter 4 Week 3 PRIMARY DATA.pptx
byshahanieabbat3
 
Pratishta Educational Society., Courses & Opportunities
byGanapathiVankudoth
 
Types of counselling Directive, Non Directive, Eclectic Counselling
byPriya Sush
 
PHARMACOLOGY 1 ( BP 404 T) Unit 1 (Cology 1)
byChetan Mali
 
How to Manage Reservation Method in Odoo 18 Inventory
byCeline George
 
Judgement Regarding Land Acquisition Act not Applicable to Encroachers.pdf
byssuser9d8e4e
 
AI Is a Tool, Not a Voice: Radio, Trust, and the Human Factor
byN.A. Shah Ansari
 
Artificial Intelligence in Research and Academic Writing, Workshop on Researc...
byProf. Vinod Kumar Kanvaria
 
Nursing care plan for Vomiting /B.Sc nsg
byDr. Sudhadevi Sadanandan
 
Holm Community Heritage at St Nicholas Kirk - 2025 AGM Minutes (30.04.2025)
byAntoine Pietri
 
Greengnorance Toolkit Module 6 Water Resources
byKarl Donert
 

statics

  • 2.
    Introduction • This chapterbuilds on chapter 3 and focuses on objects in equilibrium, ie) On the point of moving but actually remaining stationary • As in chapter 3 it involves resolving forces in different directions • Statics is important in engineering for calculating whether structures are stable
  • 4.
    Statics of aParticle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically 4N 4Sin45 Similar to chapter 3, for these types of problem you should: 1) Draw a diagram and label the forces 45° 4Cos45 30° PCos30 The particle to the PN left is in equilibrium. Calculate the magnitude of the PSin30 forces P and Q. x 2) Resolve into horizontal/vertical or parallel/perpendicular components 3) Set the sums equal to 0 (as the objects are in equilibrium, the forces acting in opposite directions must cancel out… 4) Solve the equations to find the unknown forces…  This means the horizontal and vertical forces cancel out (acceleration = 0 in both directions so F = 0) QN Resolve Horizontally Choose a direction as positive and sub in values Rearrange Divide by Cos30 Calculate 4A
  • 5.
    Statics of aParticle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically 4N 4Sin45 Similar to chapter 3, for these types of problem you should: 1) Draw a diagram and label the forces 45° 4Cos45 30° PCos30 The particle to the PN left is in equilibrium. Calculate the magnitude of the PSin30 forces P and Q. x 2) Resolve into horizontal/vertical or parallel/perpendicular components 3) Set the sums equal to 0 (as the objects are in equilibrium, the forces acting in opposite directions must cancel out… 4) Solve the equations to find the unknown forces…  This means the horizontal and vertical forces cancel out (acceleration = 0 in both directions so F = 0) P = 3.27N QN Resolve Vertically Choose a direction as positive and sub in values Add Q Calculate Q using the exact value of P from the first part You will usually need to identify which direction is solvable first, then solve the second direction after! 4A
  • 6.
    Statics of aParticle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically The diagram to the right shows a particle in equilibrium under a number of forces. Calculate the magnitudes of the forces P and Q  Start by resolving in both directions QN PN 1N QSin55 PSin40 55° QCos55 40° PCos40 x 2N Resolve Horizontally 1) 2) Choose a direction as positive and sub in values Resolve Vertically Choose a direction as positive and sub in values Simplify 4A
  • 7.
    Statics of aParticle y You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically QN PN 1N QSin55 PSin40 55° The diagram to the right shows a particle in equilibrium under a number of forces. QCos55 Calculate the magnitudes of the forces P and Q  Start by resolving in both directions 40° PCos40 x 2N 2) Replace P with the Q equivalent 1) Multiply all terms by Cos40 2) Add Cos40  You can now solve these by rearranging one and subbing it into the other! Divide by  Q = 0.769N the bracket Factorise Q on the left side Calculate 4A
  • 8.
    Statics of aParticle y QN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically PN 1N QSin55 PSin40 55° The diagram to the right shows a particle in equilibrium under a number of forces. QCos55 Calculate the magnitudes of the forces P and Q 40° PCos40 x 2N  Start by resolving in both directions 1) 1) Sub in Q (use the exact value) 2)  You can now solve these by rearranging one and subbing it into the other!  Q = 0.769N  P = 0.576N Calculate 4A
  • 9.
    Statics of aParticle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PCosθ 5Cos30 30° 5N 8N 30° 5Sin30 Resolving Parallel Use P as the positive direction and sub in values 1) 2) PSinθ 2N Rearrange to leave PCosθ Resolving Perpendicular Use P as the positive direction and sub in values Rearrange to leave PSinθ 4A
  • 10.
    Statics of aParticle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. 1) 2) PCosθ 5Cos30 30° 5N Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PSinθ 2N 8N 2) 1) 30° 5Sin30 Divide equation 2 by equation 1  Each side must be divided as a whole, not individual parts  P’s cancel, Sin/Cos = Tan Work out the fraction Use inverse Tan 4A
  • 11.
    Statics of aParticle PN You can solve problems involving particles in equilibrium by considering forces acting horizontally and vertically θ The diagram shows a particle in equilibrium on an inclined plane under the effect of the forces shown. 1) 2) PCosθ 5Cos30 30° 5N Find the magnitude of the force P and the size of angle θ.  Start by splitting forces into parallel and perpendicular directions PSinθ 2N 8N 1) 30° 5Sin30 Divide by Cosθ Sub in the exact value for θ Calculate P 4A
  • 13.
    Statics of aParticle Q You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A particle of mass 3kg is held in equilibrium by two light inextensible strings. One of the strings is horizontal, and the other is inclined at 45° to the horizontal, as shown. The tension in the horizontal string is P and in the other string is Q. Find the values of P and Q. QSin45 45° P QCos45 3g Resolve vertically Choosing Q as the positive direction, sub in values… Add 3g Divide by Sin45 Calculate 4B
  • 14.
    Statics of aParticle Q You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A particle of mass 3kg is held in equilibrium by two light inextensible strings. One of the strings is horizontal, and the other is inclined at 45° to the horizontal, as shown. The tension in the horizontal string is P and in the other string is Q. Find the values of P and Q. QSin45 45° P QCos45 3g Resolve horizontally Choosing Q as the positive direction, sub in values… Add P Sub in the value of Q from before Calculate P 4B
  • 15.
    Statics of aParticle X You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A smooth bead, Y, is threaded on a light inextensible string. The ends of the string are attached to two fixed points X and Z on the same horizontal level. The bead is held in equilibrium by a horizontal force of 8N acting in the direction ZX. Bead Y hangs vertically below X and angle XZY = 30°. Find: a) The tension in the string b) The weight of the bead Z 30° T T 8 Y TSin30 30° TCos30 Draw a diagram  Since this is only one string and it is inextensible, the tension in it will be the same  Call the mass m, since we do not know it… mg Resolve Horizontally Sub in values, choosing T as the positive direction Add 8 Divide by Cos30 Calculate 4B
  • 16.
    Statics of aParticle X You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A smooth bead, Y, is threaded on a light inextensible string. The ends of the string are attached to two fixed points X and Z on the same horizontal level. The bead is held in equilibrium by a horizontal force of 8N acting in the direction ZX. Bead Y hangs vertically below X and angle XZY = 30°. Find: a) The tension in the string b) The weight of the bead Z 30° T T 8 Y 30° TSin30 TCos30 Draw a diagram  Since this is only one string and it is inextensible, the tension in it will be the same  Call the mass m, since we do not know it… mg Resolve Vertically Sub in values, choosing T as the positive direction Add mg Sub in the value of T This is all we need! Be careful on this type of question. If particle is held by 2 different strings, the tensions may be different in each! The question asked for the weight, not the mass! (weight being mass x gravity…) 4B
  • 17.
    Statics of aParticle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. Calculate: a) The tension in AC b) The tension in BC A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60  The strings are separate so use T1 and T2 as the tensions 10g Resolving Horizontally Sub in values, choosing T2 as the positive direction Add T1Cos30 Divide by Cos60 4B
  • 18.
    Statics of aParticle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60 Resolving Vertically  The strings are separate so use T1 and T2 as the tensions 10g Sub in values, choosing T2 as the positive direction Replace T2 with the expression involving T1 Calculate: a) The tension in AC b) The tension in BC Multiply all terms by Cos60 Add 10gCos60 and factorise left side Divide by the bracket Calculate! 4B
  • 19.
    Statics of aParticle You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A small bag of mass 10kg is attached at C to the ends of two light inextensible strings AC and BC. The other ends of the strings are attached to fixed points A and B on the same horizontal line. The bag hangs in equilibrium with AC and BC inclined to the horizontal at 30° and 60° respectively as shown. Calculate: a) The tension in AC b) The tension in BC A B Draw a diagram T1 T1Sin30 T2 T2Sin60 30° C 60° T1Cos30 T2Cos60  The strings are separate so use T1 and T2 as the tensions 10g Find T2 by using the original equation… Sub in the value of T1 Calculate! 4B
  • 20.
    Statics of aParticle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. 9.8N T T 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Find the tension using the 1kg mass Resolve in the direction of T and sub in values Add 1g By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 4B
  • 21.
    Statics of aParticle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 9.8N 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Resolve Parallel to find P Choose P as the positive direction and sub in values Rearrange Divide by Cos45 Calculate 4B
  • 22.
    Statics of aParticle R You need to know when to include additional forces on your diagrams, such as weight, tension, thrust, the normal reaction and friction A mass of 3kg rests on the surface of a smooth plane inclined at an angle of 45° to the horizontal. The mass is attached to a cable which passes up the plane and passes over a smooth pulley at the top. The cable carries a mass of 1kg which hangs freely at the other end. There is a force of PN acting horizontally on the 3kg mass and the system is in equilibrium. 9.8N 9.8N P PSin45 45˚ PCos45 3gCos45 3g 45˚ 45˚ 3gSin45 1g Resolve Perpendicular to find R Choose R as the positive direction and sub in values Rearrange Calculate By modelling the cable as a light inextensible string and the masses as particles, calculate: a) The magnitude of P b) The normal reaction between the mass and the plane 4B
  • 24.
    Statics of aParticle You can also solve statics problems by using the relationship F = µR We have seen before that FMAX is the maximum frictional force possible between two surfaces, and that it will resist any force up to this amount Remember that the frictional force can be lower than this and still prevent movement In statics, FMAX is reached when a body is in limiting equilibrium, ie) on the point of moving A block of mass 3kg rests on a rough horizontal plane. The coefficient of friction between the block and the plane is 0.4. When a horizontal force PN is applied to the block, the block remains in equilibrium. a) Find the value for P for which the equilibrium is limiting b) Find the value of F when P = 8N 3g R F 3kg Resolve vertically for R 3g P Find FMAX Sub in values with R as positive Sub in values It is important to consider which Add 3g Calculate direction the object is about to move as this affects the direction the friction is acting… So if P = 11.76N, then the block is in limiting equilibrium on the point of moving For part b), if P = 8N then equilibrium is not limiting, and P will be matched by a frictional force of 8N 4C
  • 25.
    Statics of aParticle You can also solve statics problems by using the relationship F = µR A mass of 8kg rests on a rough horizontal plane. The mass may be modelled as a particle, and the coefficient of friction between the mass and the plane is 0.5. R F 8kg Draw a diagram P 60° PCos60 PSin60  Find the normal reaction as we need this for FMAX 8g Resolve Vertically Find the magnitude of the maximum force PN, which acts on this mass without causing it to move if P acts at an angle of 60° above the horizontal. Sub in values with R as positive Rearrange to find R in terms of P Find FMAX Sub in values Multiply bracket out 4C
  • 26.
    Statics of aParticle You can also solve statics problems by using the relationship F = µR A mass of 8kg rests on a rough horizontal plane. The mass may be modelled as a particle, and the coefficient of friction between the mass and the plane is 0.5. Find the magnitude of the maximum force PN, which acts on this mass without causing it to move if P acts at an angle of 60° above the horizontal. R F 8kg 8g Resolve Horizontally Draw a diagram P 60° PCos60 PSin60  Find the normal reaction as we need this for FMAX  The horizontal forces will cancel out as the block is in limiting equilibrium Sub in values with P as positive Sub in FMAX ‘Multiply out’ the bracket Add 4g If P is any greater, the block will start to accelerate. If P is any smaller, then FMAX will be less and hence the block will not be in limiting equilibrium Factorise P on the left side Divide by the bracket Calculate 4C
  • 27.
    Statics of aParticle R F You can also solve statics problems by using the relationship F = µR A box of mass 10kg rests in limiting equilibrium on a rough plane inclined at 20° above the horizontal. Find the coefficient of friction between the box and the plane. 10gCos20 10g 10gSin20 Resolving Perpendicular Sub in values with R as positive  Draw a diagram Rearrange  We need to find FMAX so begin by calculating the normal reaction Finding FMAX Sub in R and leave µ 4C
  • 28.
    Statics of aParticle R F You can also solve statics problems by using the relationship F = µR A box of mass 10kg rests in limiting equilibrium on a rough plane inclined at 20° above the horizontal. Find the coefficient of friction between the box and the plane.  Draw a diagram  We need to find FMAX so begin by calculating the normal reaction  Now you can resolve Parallel to find µ 10gCos20 10g 10gSin20 Resolving Parallel Sub in values with ‘down the plane’ as positive Sub in FMAX Add µ(10gCos20) Divide by the bracket Calculate 4C
  • 29.
    Statics of aParticle You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane Find the other trig ratios – this will be useful later! Hyp 13 5 Opp θ 12 Adj So the opposite side is 5 and the hypotenuse is 13  Use Pythagoras to find the missing side!  Now you can work out the other 2 trig ratio… 4C
  • 30.
    Statics of aParticle R P You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) 2g θ F θ 2gCosθ 2gSinθ Start with a diagram  P is acting up the plane, on the point of causing the box to move  Friction is opposing this movement Resolving Perpendicular for R Sub in values with R as the positive direction Moving up the plane Rearrange b) Moving down the plane Finding FMAX Sub in values Remove the bracket 4C
  • 31.
    Statics of aParticle R P You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2gCosθ 2g θ F θ 2gSinθ Start with a diagram  P is acting up the plane, on the point of causing the box to move  Friction is opposing this movement Resolving Parallel for P Sub in values with P as the positive direction Sub in F Rearrange for P Sub in Sinθ and Cosθ Calculate 4C
  • 32.
    Statics of aParticle F P R You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2gCosθ 2g θ F θ 2gSinθ Resolving Parallel for P We now need to adjust the diagram for part b)  Now, as the particle is on the point of sliding down the plane, the friction will act up the plane instead…  FMAX will be the same as before as we haven’t changed any vertical components Sub in values with P as the positive direction Replace F Rearrange Sub in Sinθ and Cosθ Calculate 4C
  • 33.
    Statics of aParticle F P R You can also solve statics problems by using the relationship F = µR A parcel of mass 2kg is placed on a rough plane inclined at an angle θ to the horizontal where Sinθ = 5/13. The coefficient of friction is 1/3. Find the magnitude of force PN, acting up the plane, that causes the parcel to be in limiting equilibrium and on the point of: a) Moving up the plane b) Moving down the plane 2g θ θ 2gCosθ 2gSinθ We now need to adjust the diagram for part b)  Now, as the particle is on the point of sliding down the plane, the friction will act up the plane instead…  FMAX will be the same as before as we haven’t changed any vertical components A force of 13.57N up the plane is enough to bring the parcel to the point of moving in that direction. Any more will overcome the combination of gravity and friction and the parcel will start moving up A force of 1.51N up the plane is enough, when combined with friction, to prevent the parcel from slipping down the plane and hold it in place. Any less and the parcel will start moving down. 4C
  • 34.
    Statics of aParticle 15N You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. Draw a diagram – ensure you include all forces and their components in the correct directions R 15° 1.6g F 45° 45° 1.6gCos45 1.6gSin45  The box is on the point of moving up, so friction is acting down the plane  Find the normal reaction and use it to find FMAX Resolving Perpendicular Sub in values with R as the positive direction Find the value of the coefficient of friction between the box and the plane. Rearrange Finding FMAX Sub in values 4C
  • 35.
    Statics of aParticle 15N You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. R 15° 1.6g F 45° 45° 1.6gCos45 Draw a diagram – ensure you include all forces and their components in the correct directions  Now resolve parallel to create an equation you can solve for μ. 1.6gSin45 Resolving Parallel Sub in values with ‘up’ the plane as the positive direction Replace F Find the value of the coefficient of friction between the box and the plane. Divide by the bracket Add μ term Calculate! 4C
  • 36.
    Statics of aParticle 10N 15N 15° You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane.  Calculate the new FMAX, first finding the new R… R 1.6g F 45° 45° 1.6gCos45 1.6gSin45 Resolving Perpendicular Sub in values with R as the positive direction Find the value of the coefficient of friction between the box and the plane.  The tension is reduced to 10N. Determine the magnitude and direction of the frictional force in this case Update the diagram (or re-draw it!) Rearrange Finding FMAX Sub in values Calculate 4C
  • 37.
    Statics of aParticle 10N 15° You can also solve statics problems by using the relationship F = µR A box of mass 1.6kg is placed on a rough plane, inclined at 45° to the horizontal. The box is held in equilibrium by a light inextensible string, which makes an angle of 15° with the plane. When the tension in the string is 15N, the box is in limiting equilibrium and about to move up the plane. Find the value of the coefficient of friction between the box and the plane.  The tension is reduced to 10N. Determine the magnitude and direction of the frictional force in this case Update the diagram (or re-draw it!)  Calculate the new FMAX, first finding the new R… R 1.6g F 45° 45° 1.6gCos45 1.6gSin45  Add up the forces acting parallel to the plane (ignoring friction for now) Resolving Parallel (without friction) The force up the plane will be given by: As this is negative, then without friction, there is an overall force of 1.428N acting down the plane  Therefore, friction will oppose this by acting up the plane  As FMAX = 4.012N, the box will not move and is not in limiting equilibrium 4C
  • 38.
    Summary • We havelearnt about resolving forces when a particle is in limiting equilibrium • We have seen when and how to include additional forces such as tension and friction • We have looked at situations where friction acts in different directions