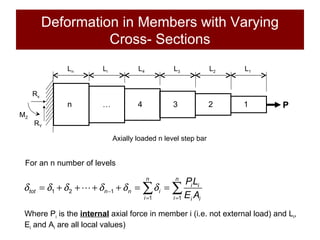
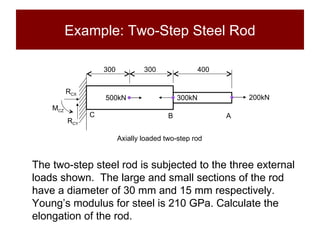
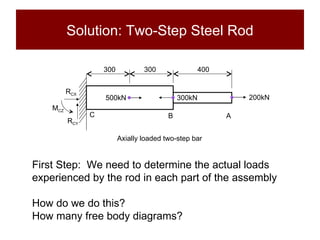
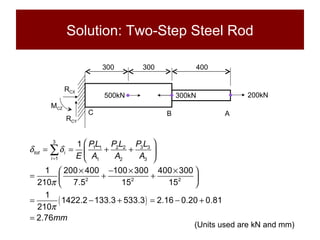
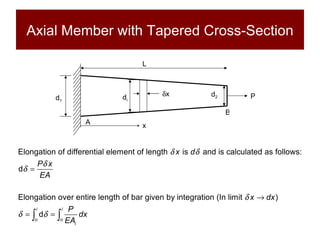
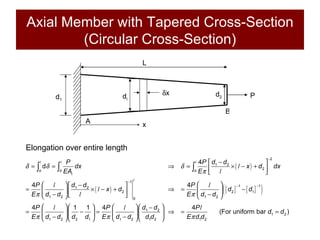
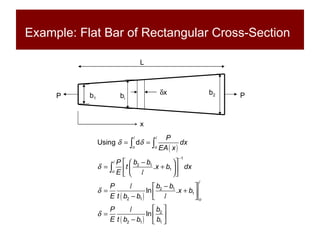
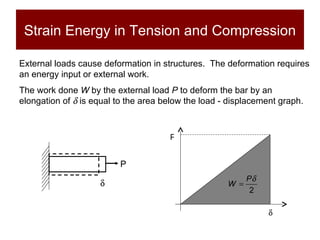
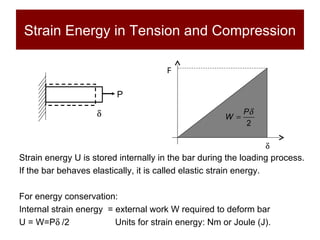
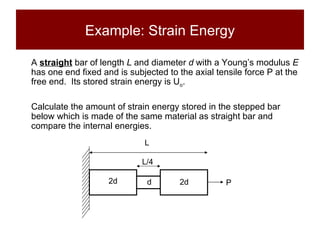
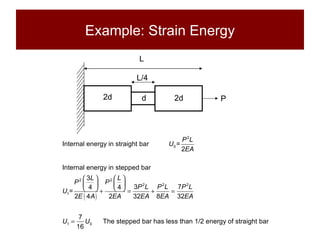
This document discusses the analysis of axially loaded structural members, focusing on the deformation of stepped and tapered rods under tension, and introduces the concept of strain energy. It includes mathematical equations for calculating elongation and strain energy in members with varying cross-sections and provides examples with detailed solutions. The document is part of educational material from Loughborough University, emphasizing the mechanics of materials under axial loads.

1. Section 6 Axially Loaded Structural Members This section will introduce how to solve problems of axially loaded members such as stepped and tapered rods loaded in tension. The concept of strain energy will also be introduced. © Loughborough University 2010. This work is licensed under a Creative Commons Attribution 2.0 Licence .

2. Contents Axially Loaded Structural Members Deformation of Axially Loaded Members Deformation in Members with Varying Cross- Sections Example: Two-Step Steel Rod Solution: Two-Step Steel Rod Two-Step Steel Rod: FBD Solution: Two-Step Steel Rod Axial Member with Tapered Cross-Section Axial Member with Tapered Cross-Section (Circular Cross-Section) Axial Member with Tapered Cross-Section (Rectangular Cross-Section) Example: Flat Bar of Rectangular Cross-Section Strain Energy in Tension and Compression Strain Energy – Axial Loading Strain Energy – Shear Loading Example: Strain Energy Credits & Notices

3. Axially Loaded Structural Members In previous lectures we have looked at stress and strain behaviour of materials and the deformation caused by axial loads We will now look at the deformation caused by axial loads in structures with a stepped or tapered geometry This will then lead into the work done by the external loads and how strain energy is calculated.

4. Deformation of Axially Loaded Members The term EA/L is the stiffness of the member so we can rewrite the equation as The deformation of a structural member, with known geometry, and subjected to an axial load can be determined by using the equation from the notes in Section 3 Parameter k is called stiffness (sometimes or spring constant). The reciprocal of the stiffness, k -1 , is called compliance.

5. Deformation in Members with Varying Cross- Sections Individual elongations  1 and  2 are added algebraically to give an overall elongation of the entire system as Axially loaded stepped member (P i , L i , E i and A i are local values e.g. P i is internal force) L 2 L 1 P P B B A C (P 2 ) (P 1 ) R CX R CY M CZ

6. Deformation in Members with Varying Cross- Sections For an n number of levels Axially loaded n level step bar R x R Y M Z Where P i is the internal axial force in member i (i.e. not external load) and L i , E i and A i are all local values) P n … 4 3 2 1 L n L i L 4 L 3 L 2 L 1

7. Example: Two-Step Steel Rod The two-step steel rod is subjected to the three external loads shown. The large and small sections of the rod have a diameter of 30 mm and 15 mm respectively. Young’s modulus for steel is 210 GPa. Calculate the elongation of the rod. Axially loaded two-step rod 300 200kN 300kN B A C R CX R CY M CZ 300 400 500kN

8. Solution: Two-Step Steel Rod First Step: We need to determine the actual loads experienced by the rod in each part of the assembly How do we do this? How many free body diagrams? Axially loaded two-step bar 300 200kN 300kN B A C R CX R CY M CZ 300 400 500kN

9. Two-Step Steel Rod: FBD Red lines show cuts to establish internal forces 2 1 3 200kN P 1 Internal force P 1 = 200kN (tension) 200kN 300kN P 2 P 2 = -100kN (compression) 200kN 300kN 500kN P 3 P 3 = 400kN (tension) Cut 1 1 Cut 2 2 Cut 3 3 2 1 3 200kN 300kN B A C R CX R CY M CZ 500kN

10. Solution: Two-Step Steel Rod (Units used are kN and mm) 300 200kN 300kN B A C R CX R CY M CZ 300 400 500kN

11. Axial Member with Tapered Cross-Section  x L A B x d 1 d 2 d i P

12. Axial Member with Tapered Cross-Section (Circular Cross-Section) Force equilibrium at any cross section shows P is constant along length Taper is linear so diameter d of rod at distance x is d i Area A of rod at distance x is A i  x L A B x d 1 d 2 d i P

13. Axial Member with Tapered Cross-Section (Circular Cross-Section) Elongation over entire length  x L A B x d 1 d 2 d i P

14. Axial Member with Tapered Cross-Section (Rectangular Cross-Section) A flat bar of rectangular cross section is subjected to the tensile forces P shown. It has a length L and a constant thickness t with Young’s modulus E . The width of the bar varies linearly from b 1 at left end to b 2 at right end. Determine the elongation of the bar.  x L x b 1 b 2 b i P P

15. Example: Flat Bar of Rectangular Cross-Section  x L x b 1 b 2 b i P P

16. Example: Flat Bar of Rectangular Cross-Section  x L x b 1 b 2 b i P P

17. Strain Energy in Tension and Compression External loads cause deformation in structures. The deformation requires an energy input or external work. The work done W by the external load P to deform the bar by an elongation of  is equal to the area below the load ­ displacement graph . P   P

18. Strain Energy in Tension and Compression Strain energy U is stored internally in the bar during the loading process. If the bar behaves elastically, it is called elastic strain energy. For energy conservation: Internal strain energy = external work W required to deform bar U = W=P  /2 Units for strain energy: Nm or Joule (J). P   P

19. Strain Energy – Axial Loading

20. Strain Energy – Shear Loading

21. Example: Strain Energy A straight bar of length L and diameter d with a Young’s modulus E has one end fixed and is subjected to the axial tensile force P at the free end. Its stored strain energy is U o . Calculate the amount of strain energy stored in the stepped bar below which is made of the same material as straight bar and compare the internal energies. L/4 L 2d 2d d P

22. Example: Strain Energy L/4 L 2d 2d d P

23. This resource was created by Loughborough University and released as an open educational resource through the Open Engineering Resources project of the HE Academy Engineering Subject Centre. The Open Engineering Resources project was funded by HEFCE and part of the JISC/HE Academy UKOER programme. © 2010 Loughborough University. Except where otherwise noted this work is licensed under a Creative Commons Attribution 2.0 Licence . The name of Loughborough University, and the Loughborough University logo are the name and registered marks of Loughborough University. To the fullest extent permitted by law Loughborough University reserves all its rights in its name and marks, which may not be used except with its written permission. The JISC logo is licensed under the terms of the Creative Commons Attribution-Non-Commercial-No Derivative Works 2.0 UK: England & Wales Licence. All reproductions must comply with the terms of that licence. The HEA logo is owned by the Higher Education Academy Limited may be freely distributed and copied for educational purposes only, provided that appropriate acknowledgement is given to the Higher Education Academy as the copyright holder and original publisher. Credits