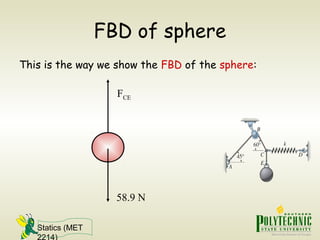
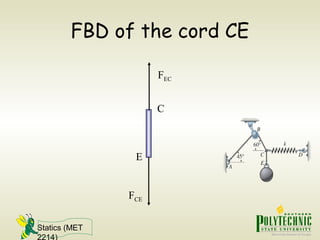
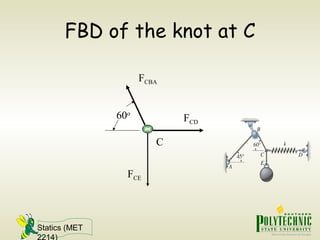
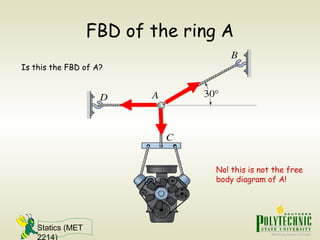
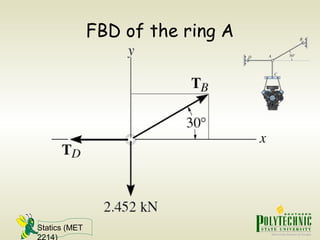
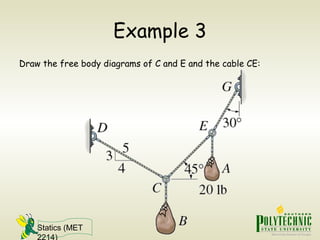
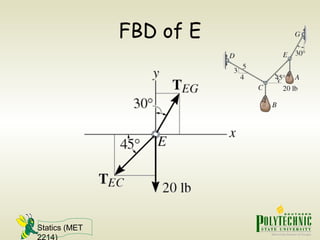
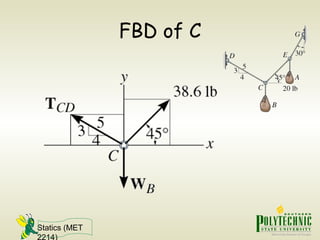
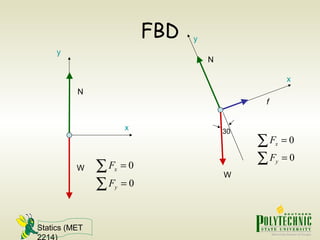
This document provides an introduction to statics and static equilibrium for particles. It defines key terms like particles, equilibrium, and free-body diagrams. It explains that a particle is in equilibrium if the net force acting on it is zero. Free-body diagrams show all forces acting on a particle and are used to apply the equations of equilibrium to solve problems. Examples are provided of drawing free-body diagrams and using them to determine unknown forces on mechanical components in static equilibrium.

1. Statics (MET
2214)
Statics of Particles
MET 2214

2. Statics (MET
2214)
Static Equilibrium for a Particle
Objective: To introduce the concept of the free-body
diagram for a particle and to show how to solve
particle equilibrium problems using the equations of
equilibrium.
A particle: An object with inertia (mass) but of
negligible dimensions.
A particle at rest: A particle is at rest if originally at
rest or has a constant velocity if originally in motion.

3. Statics (MET
2214)
Equilibrium equations for a particle
A particle is in equilibrium if the resultant of ALL
forces acting on the particle is equal to zero.
(Newton’s first law is that a body at rest is not
subjected to any unbalanced forces).
Sum of all forces acting
on a particle = 0F =∑

4. Statics (MET
2214)
Equilibrium equations in component form
In a rectangular coordinate system the equilibrium
equations can be represented by three scalar
equations:
0
0
0
x
y
z
F
F
F
=
=
=
∑
∑
∑

5. Statics (MET
2214)
Free-Body Diagram (FBD):
To apply equilibrium equations we must account for all
known and unknown forces acting on the particle.
The best way to do this is to draw a free-body diagram of
the particle.
FBD: A diagram showing the particle under consideration
and all the forces and moments acting on this particle.
This is a sketch that shows the particle “free” from its
surroundings with all the forces acting on it.

6. Statics (MET
2214)
Parallelogram Law
Copyright of Ohio University
Two forces on a body can be replaced by a single force called
the resultant by drawing the diagonal of the parallelogram
with sides equivalent to the two forces.

7. Statics (MET
2214)
Principal of Transmissibility
The conditions of equilibrium or motion of a body remain unchanged
if a force on the body is replaced by a force of the same
magnitude and direction along the line of action of the original
force.

8. Statics (MET
2214)
Mechanical components
String or cable: A mechanical device that can only
transmit a tensile force along itself.

9. Statics (MET
2214)
Mechanical components
Linear spring: A mechanical device which exerts a force along its
line of action and proportional to its extension (F = kX).
K is constant of proportionality which is a measure of stiffness or
strength.

10. Statics (MET
2214)
Mechanical components
Cables:
Cables are assumed to have negligible weight and they cannot stretch.
They can only support tension or pulling (you can’t push on a rope!).
Frictionless pulleys:
Pulleys are assumed to be frictionless.

11. Statics (MET
2214)
Mechanical components
A continuous cable passing over a
frictionless pulley must have tension force
of a constant magnitude.
The tension force is always directed in the
direction of the cable.
For a frictionless pulley in static equilibrium,
the tension in the cable is the same on
both sides of the pulley.

12. Statics (MET
2214)
Force types
Force types:
Active Forces - tend to set the particle in motion.
Reactive Forces - result from constraints or supports
and tend to prevent motion.
Active force
Reactive
force Active force
Reactive force

13. Statics (MET
2214)
Free Body Diagram (FBD)
How to draw a Free Body Diagram:
Draw outlined shape - Imagine the particle isolated
or cut “free” from its surroundings
Show all forces and moments - Include “active
forces” and “reactive forces”. Place each force and
couple at the point that it is applied.
Identify each force:
Known forces labeled with proper magnitude and direction.
Letters used for unknown quantities.
Add any relevant dimensions onto your picture.

14. Statics (MET
2214)
FBD

15. Statics (MET
2214)
FBD
F.B.D of the ring A:

16. Statics (MET
2214)
Example 1
The sphere has a mass of 6 kg and is supported as shown. Draw a
free-body diagram of the sphere, cord CEsphere, cord CE, and the knot at C.the knot at C.

17. Statics (MET
2214)
Sphere
There are two forces acting on the sphere. These are its weight
and the force of cord CE.
The weight is: W = 6 kg (9.81 m/s2
) = 58.9 N.

18. Statics (MET
2214)
FBD of sphere
This is the way we show the FBD of the sphere:
FCE
58.9 N

19. Statics (MET
2214)
Cord CE
There are two forces acting on the cord. These are the force of
the sphere, and the force of the knot. A cord is a tension only
member. Newton’s third law applies.

20. Statics (MET
2214)
FBD of the cord CE
FCE
FEC
C
E

21. Statics (MET
2214)
Knot at C
There are three forces acting on the knot at C. These are the
force of the cord CBA, and the force of the cord CE, and the
force of the spring CD.

22. Statics (MET
2214)
FBD of the knot at C
FCE
FCBA
FCD
C
60o

23. Statics (MET
2214)
Example 2
Draw the FBD diagram of the ring A:
W= 2.452 KN

24. Statics (MET
2214)
FBD of the ring A
Is this the FBD of A?
No! this is not the free
body diagram of A!

25. Statics (MET
2214)
FBD of the ring A

26. Statics (MET
2214)
Example 3
Draw the free body diagrams of C and E and the cable CE:

27. Statics (MET
2214)
FBD of E

28. Statics (MET
2214)
FBD of C

29. Statics (MET
2214)
FBD of cable EC

30. Statics (MET
2214)
Example 4
Draw the FBD of ring A.
W=78.5 N

31. Statics (MET
2214)
FBD of A

32. Statics (MET
2214)
Part 2
Applying the Equilibrium
Equations

33. Statics (MET
2214)
FBD
Draw the free body diagrams:
W
N
W
N
f
Normal force = The force you have when there is a contact between surfaces
(the ball is in contact with the ground).
Friction force = You have this when the surface in contact is not frictionless and the
friction prevents the motion of the object.
30

34. Statics (MET
2214)
FBD
0
0
x
y
F
F
=
=
∑
∑
W
N
W
N
f
30
0
0
x
y
F
F
=
=
∑
∑
x
y
x
y

35. Statics (MET
2214)
yFBD
W
N
N
f
N = W
N - W.cos 30 = 0
f - W.sin 30 = 0
W.cos30
W.sin30
x
x
y

36. Statics (MET
2214)
Example 2:
Determine the tension in cables AB and AD for equilibrium of
the 250 kg engine.
FBD of the ring A

37. Statics (MET
2214)
B
0, cos30 0
0, sin30 2.452 0
Solving for T :
sin30 2.452 , 4.90
Subsituting into the first equation:
4.25
x B D
y B
B B
D
F T T
F T kN
T kN T kN
T kN
= − =
= − =
= =
=
∑
∑
Solution of Example 2
According to the free body diagram of the ring A, we have three forces
acting on the ring. The forces TB and TD have unknown magnitudes but
known directions. Cable AC exerts a downward force on A equal to:
W = (250kg)(9.81m/s2
) = 2452N = 2.245KN
TBcos30
TBsin30