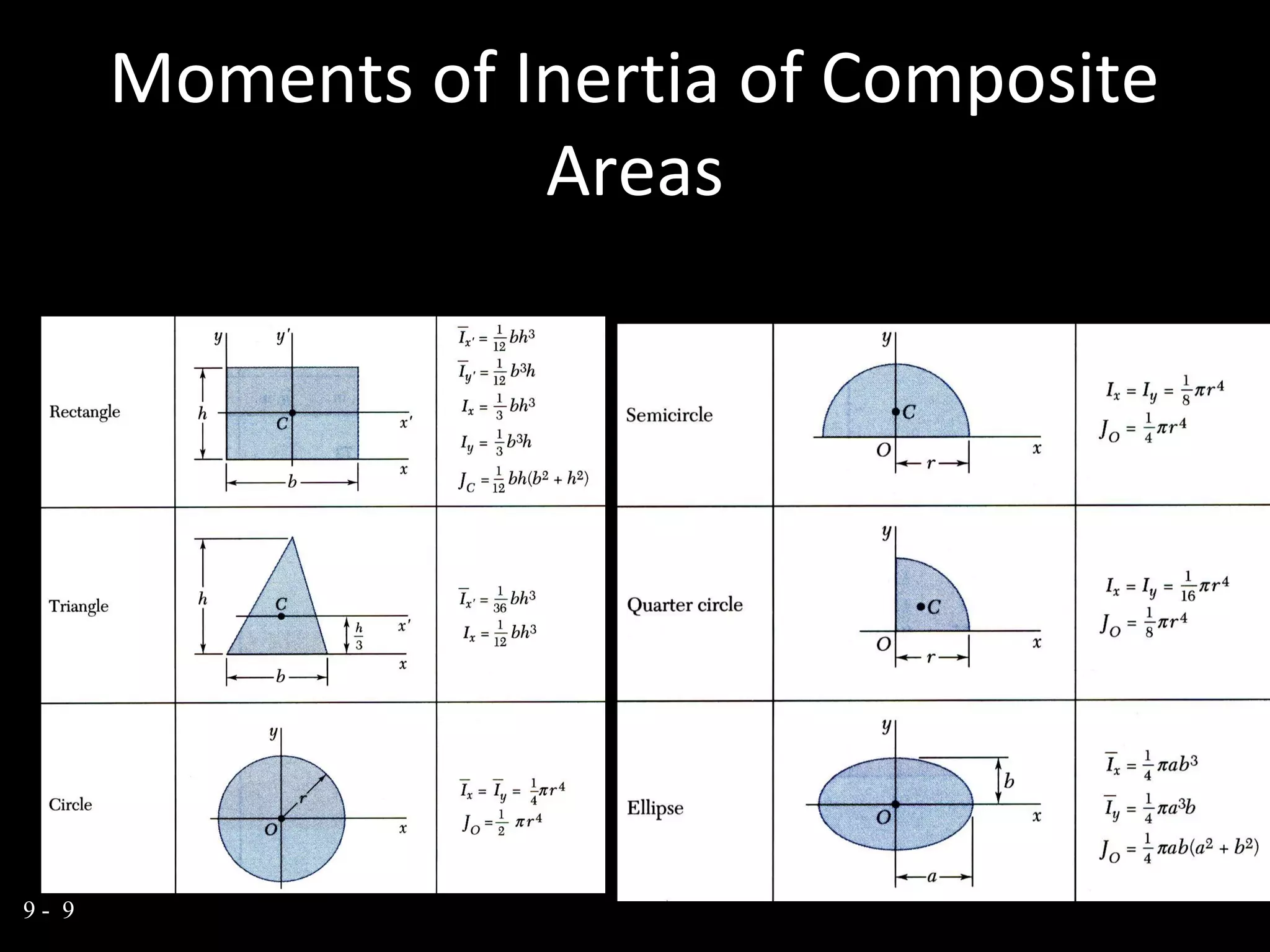
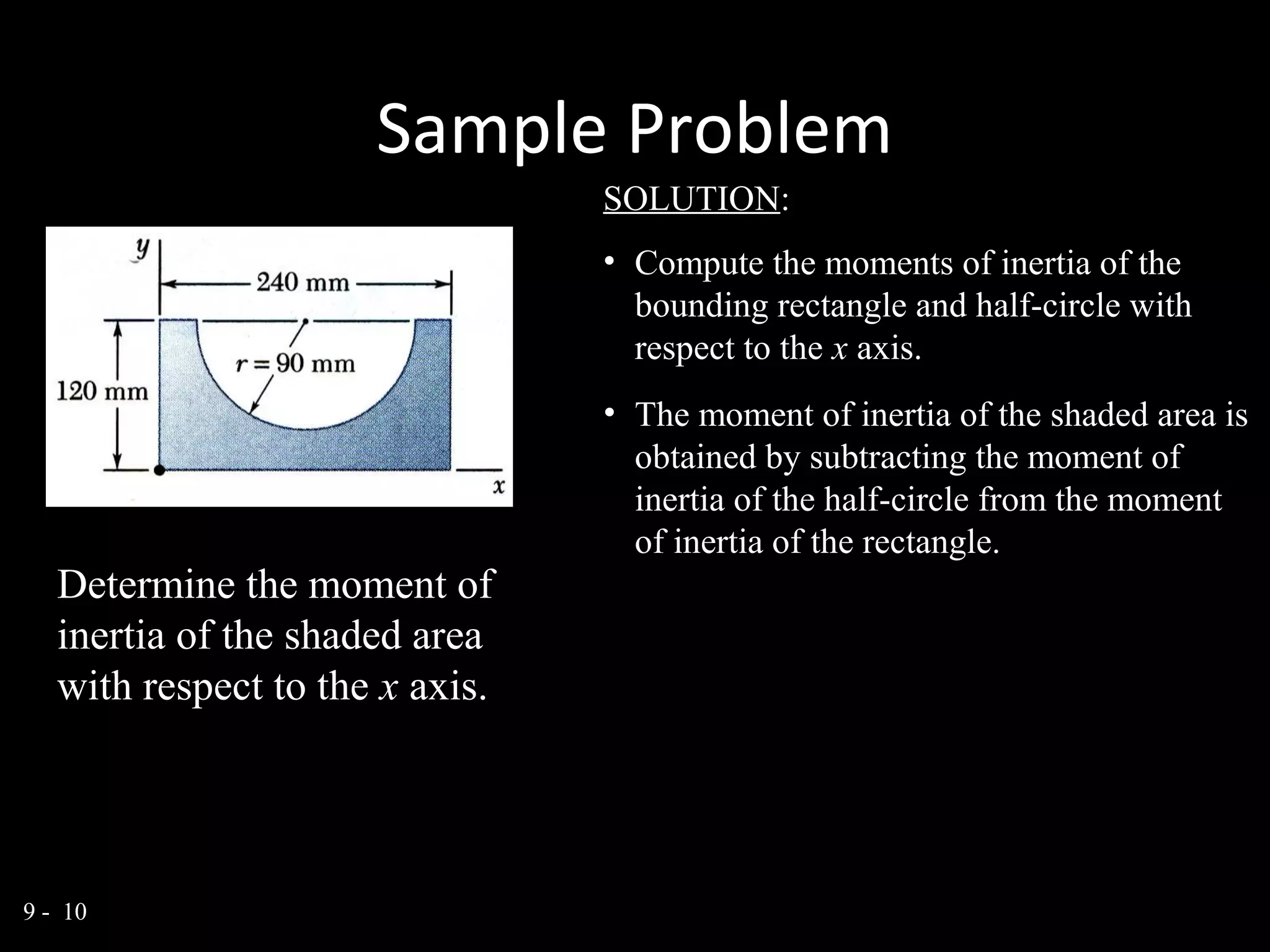
Moment of inertia (I) is a property of an object that represents its resistance to angular acceleration about an axis. I depends on both the mass of the object and how far its mass is distributed from the axis of rotation. Mathematically, I is defined as the sum of the mass of each particle multiplied by the square of its distance from the axis. An object has three principal axes with maximum, minimum, and intermediate moments of inertia. Composite areas have moments of inertia that can be calculated by subtracting or adding the I values of individual shapes about an axis.

1. Moment of Inertia ( I )
The property of an object that serves as a
resistance to angular motion.
1
BY
Usman Sajid Sohrani

2. Moment of Inertia ( I ) ≈ Mass
• Moment of inertia is affected by both the mass
and how the mass is distributed relative to the
axis of rotation.
• Unlike mass which remains constant regardless of
the direction of motion, the moment of inertia of
an object changes depending on the axis of
rotation.
2

3. Mathematically Defining I
• An object can be thought to be composed of many
particles of mass. Hence,
3
2
1
iia rmI
N
i
∑
=
=
• IIaa = moment of inertia about axis a= moment of inertia about axis a
• mmii = mass of particle i= mass of particle i
• rrii = radius from particle i to the axis of rotation= radius from particle i to the axis of rotation
• Each particle provides some resistance toEach particle provides some resistance to
change in angular motion.change in angular motion.
• The units are mass * squared length: kg*mThe units are mass * squared length: kg*m22

4. Calculate I for the baseball bat using
4
0.4 m0.4 m
0.8 m0.8 m
2
1
iia rmI
N
i
∑
=
=
0.4 m0.4 m 0.4 m0.4 m
1 kg1 kg 2 kg2 kgaa
11
1 kg1 kg bb 2 kg2 kg
22

5. Solutions
5
2
1
iia rmI
N
i
∑
=
=
1 IIaa = (1 kg)(0.4 m)= (1 kg)(0.4 m)22
+ (2 kg)(0.8 m)+ (2 kg)(0.8 m)22
IIaa = 1.44 kg*m= 1.44 kg*m22
2 IIbb = (1 kg)(0.4 m)= (1 kg)(0.4 m)22
+ (2 kg)(0.4 m)+ (2 kg)(0.4 m)22
IIbb = 0.48 kg*m= 0.48 kg*m22

6. Radius of Gyration (k)
• The distance from the axis of rotation to a point where all
of the mass can be concentrated to yield the same
resistance to angular motion.
• An averaging out of the radii (ri) of all the mass particles.
This allows all the mass to be represented by a single
radius (k).
6
2
aa mkI =
• The distribution of an object’s mass has a muchThe distribution of an object’s mass has a much
greater affect on the moment of inertia thangreater affect on the moment of inertia than
mass.mass.

7. 3 Principal Axes for any Object
7
Maximum MomentMoment of Inertia Axis (Imax)
Axis that has the largest moment of inertiainertia
Minimum Moment of Inertia Axis (Minimum Moment of Inertia Axis (IIminmin))
Axis that has the smallest moment of inertiaAxis that has the smallest moment of inertia
Intermediate Moment of Inertia Axis (Iint)
Has an intermediate moment of inertia. Determined
not by its moment of inertia value, but rather because
it is perpendicular to the both Imax and Imin.
Note: All three axes are perpendicular to each otherNote: All three axes are perpendicular to each other

8. 3 Principal Axes for a Human in
Anatomical Position
8
Transverse AxisTransverse Axis
LongitudinalLongitudinal
AxisAxis
Frontal Axis
Frontal =Frontal = IImaxmax
(Cartwheel)(Cartwheel)
Transverse =Transverse = IIintint
(Back flip)(Back flip)
Longitudinal =Longitudinal = IIminmin
(Discus throw)(Discus throw)

9. Moments of Inertia of Composite
Areas
9 - 9

10. Sample Problem
9 - 10
Determine the moment of
inertia of the shaded area
with respect to the x axis.
SOLUTION:
• Compute the moments of inertia of the
bounding rectangle and half-circle with
respect to the x axis.
• The moment of inertia of the shaded area is
obtained by subtracting the moment of
inertia of the half-circle from the moment
of inertia of the rectangle.

11. Sample Problem
9 - 11
SOLUTION:
• Compute the moments of inertia of the bounding
rectangle and half-circle with respect to the x axis.
Rectangle:
( )( ) 46
3
13
3
1
mm102.138120240 ×=== bhIx
Half-circle:
moment of inertia with respect to AA’,
( ) 464
8
14
8
1 mm1076.2590 ×===′ ππrI AA
( )( )
( )
23
2
2
12
2
1
mm1072.12
90
mm81.8a-120b
mm2.38
3
904
3
4
×=
==
==
===
ππ
ππ
rA
r
a
moment of inertia with respect to x’,
( )( )
46
362
mm1020.7
1072.121076.25
×=
××=−= ′′ AaII AAx
moment of inertia with respect to x,
( )( )
46
2362
mm103.92
8.811072.121020.7
×=
×+×=+= ′ AbII xx

12. Sample Problem
9 - 12
46
mm109.45 ×=xI
xI = 46
mm102.138 × − 46
mm103.92 ×