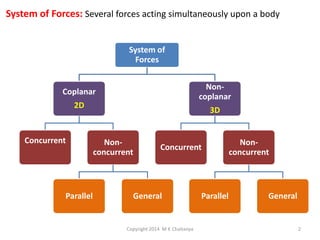
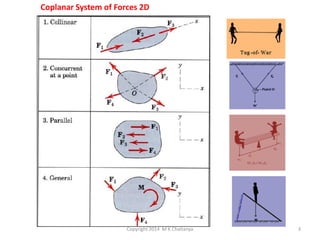
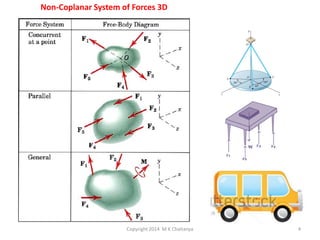
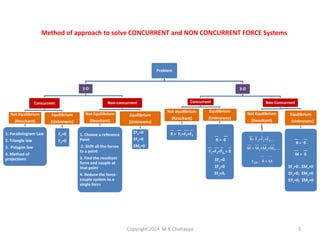
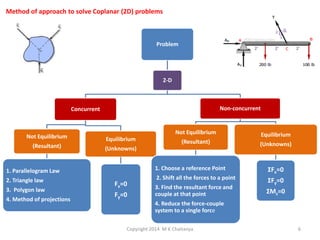
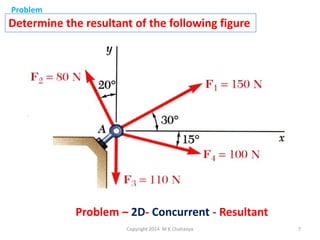
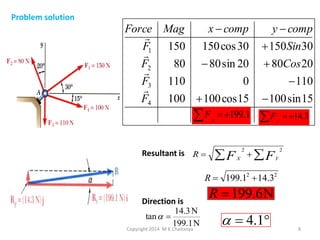
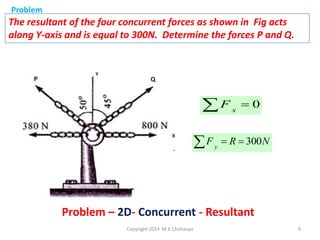
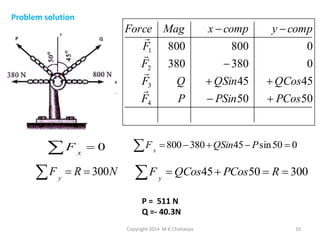
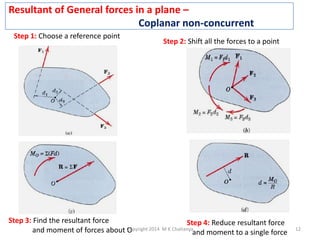
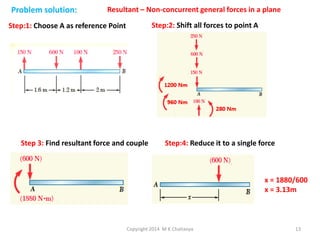
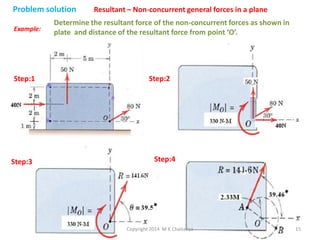
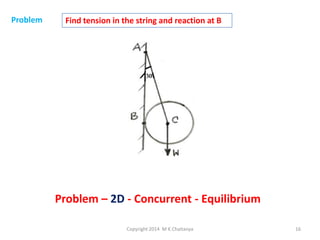
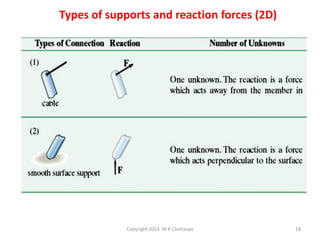
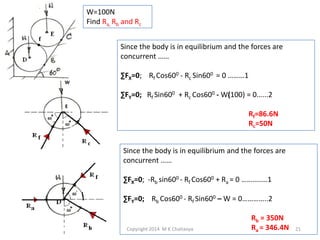
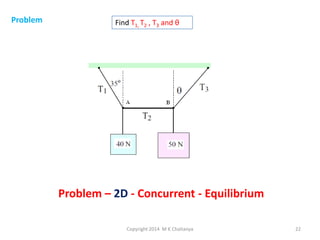
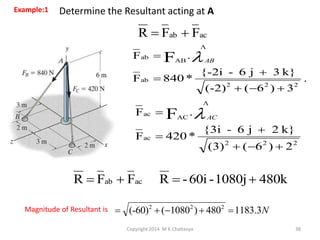
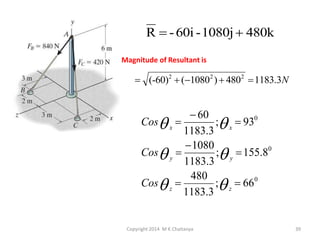
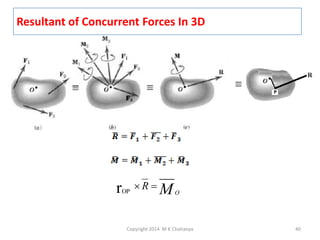
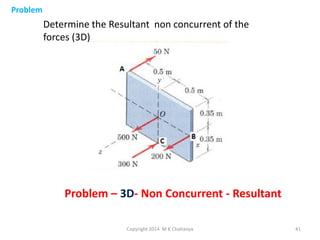
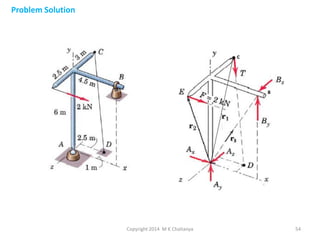
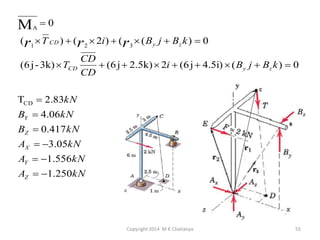
The document discusses the principles and methods of engineering mechanics, specifically focusing on systems of forces, both coplanar and non-coplanar, and how to analyze them in 2D and 3D contexts. It includes problem-solving approaches, equations of equilibrium, and examples to illustrate the calculation of resultant forces and reactions at supports under varied scenarios. Additionally, it presents detailed solutions to numerous problems involving different force systems and equilibrium conditions.

1. ENGINEERING MECHANICS
K Chaitanya Mummareddy
M.Tech, IITG
Associate Professor and
HOD of Mechanical Engineering
Malineni Perumallu Educational
Society’s group of Institutions
Guntur
Copyright 2014 M K Chaitanya
1

2. System of Forces: Several forces acting simultaneously upon a body
System of
Forces
Noncoplanar
Coplanar
2D
Concurrent
Parallel
3D
Nonconcurrent
Concurrent
General
Copyright 2014 M K Chaitanya
Parallel
Nonconcurrent
General
2

3. Coplanar System of Forces 2D
Copyright 2014 M K Chaitanya
3

4. Non-Coplanar System of Forces 3D
Copyright 2014 M K Chaitanya
4

5. Method of approach to solve CONCURRENT and NON CONCURRENT FORCE Systems
Problem
2-D
3-D
Non-concurrent
Concurrent
Equilibrium
Not Equilibrium
(Resultant)
(Unknowns)
(Resultant)
1. Parallelogram Law
Fx=0
2. Triangle law
Fy=0
1. Choose a reference
Point
Not Equilibrium
3. Polygon law
4. Method of
projections
2. Shift all the forces
to a point
Equilibrium
(Unknowns)
ΣFx=0
Concurrent
Non Concurrent
Not equilibrium
Equilibrium
(Resultant)
(Unknowns)
--- --- --- -R = F1+F2+F3
ΣFy=0
ΣMz=0
3. Find the resultant
force and couple at
that point
--- --R= 0
--- --- -- -F1+F2+F3,,= 0
ΣFx=0
ΣFy=0
ΣFz=0,
4. Reduce the forcecouple system to a
single force
Not Equilibrium
(Resultant)
--- -- -- -R= F1+F2+F3….
--- --- --- --M = M1+M2+M3....
--- --rOPͯ R = M
Equilibrium
(Unknowns)
--- --R= 0
--- --M= 0
ΣFx=0 , ΣMx=0
ΣFy=0, ΣMy=0
ΣFz=0, ΣMz=0
Copyright 2014 M K Chaitanya
5

6. Method of approach to solve Coplanar (2D) problems
Problem
2-D
Non-concurrent
Concurrent
Not Equilibrium
Not Equilibrium
Equilibrium
(Resultant)
Equilibrium
(Resultant)
(Unknowns)
(Unknowns)
1. Choose a reference Point
1. Parallelogram Law
2. Triangle law
3. Polygon law
4. Method of projections
Fx=0
Fy=0
ΣFx=0
2. Shift all the forces to a point
ΣFy=0
3. Find the resultant force and
couple at that point
ΣMz=0
4. Reduce the force-couple
system to a single force
Copyright 2014 M K Chaitanya
6

7. Problem
Determine the resultant of the following figure
Problem – 2D- Concurrent - Resultant
Copyright 2014 M K Chaitanya
7

8. Problem solution
Force Mag
x  comp

F1 150 150 cos 30

F2
80  80 sin 20

F3 110
0

F4 100  100 cos 15
F
Resultant is R 
x
 199.1
F
2
X
y  comp
 150 Sin30
 80Cos 20
 110
 100 sin 15
F
y
  FY
 14.3
2
R  199.12  14.32
Direction is
14.3 N
tan  
199.1 N
Copyright 2014 M K Chaitanya
R  199.6N
  4.1
8

9. Problem
The resultant of the four concurrent forces as shown in Fig acts
along Y-axis and is equal to 300N. Determine the forces P and Q.
F
F
y
x
0
 R  300 N
Problem – 2D- Concurrent - Resultant
Copyright 2014 M K Chaitanya
9

10. Problem solution
Force Mag

F1 800

F2 380

F3
Q

F4
P
F
F
y
x
0
 R  300 N
F
x
F
x  comp
800
 380
 QSin45
 PSin 50
y  comp
0
0
 QCos45
 PCos 50
 800  380  QSin45  P sin 50  0
y
 QCos45  PCos 50  R  300
P = 511 N
Q =- 40.3N
Copyright 2014 M K Chaitanya
10

11. Problem
Determine the resultant of the following figure
Problem – 2D- Non Concurrent - Resultant
Copyright 2014 M K Chaitanya
11

12. Resultant of General forces in a plane –
Coplanar non-concurrent
Step 1: Choose a reference point
Step 3: Find the resultant force
and moment of forces about Copyright 2014
O
Step 2: Shift all the forces to a point
Step 4: Reduce resultant force
and moment to a single force
M K Chaitanya
12

13. Problem solution:
Resultant – Non-concurrent general forces in a plane
Step:2: Shift all forces to point A
Step:1: Choose A as reference Point
Step 3: Find resultant force and couple
Step:4: Reduce it to a single force
x = 1880/600
x = 3.13m
Copyright 2014 M K Chaitanya
13

14. Problem
Determine the resultant of the following figure
Problem – 2D- Non Concurrent - Resultant
Copyright 2014 M K Chaitanya
14

15. Problem solution
Example:
Step:1
Step:3
Resultant – Non-concurrent general forces in a plane
Determine the resultant force of the non-concurrent forces as shown in
plate and distance of the resultant force from point ‘O’.
Step:2
Step:4
Copyright 2014 M K Chaitanya
15

16. Problem
Find tension in the string and reaction at B
Problem – 2D - Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
16

17. EQUATIONS OF EQUILIBRIUM
Copyright 2014 M K Chaitanya
17

18. Types of supports and reaction forces (2D)
Copyright 2014 M K Chaitanya
18

19. Problem solution
Find T, Rb
FBD of C
W=30N
Since the body is in equilibrium and the forces are concurrent ……
∑FX=0; Rb - T Cos600 = 0 ……………1
T= 34.64N
∑FY=0; T Sin600 – W= 0 ……………….2
Rb = 17.32N
Copyright 2014 M K Chaitanya
19

20. Problem
Find the reactions at A,B,C,D AND at F, Given W=100N
Problem – 2D - Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
20

21. W=100N
Find Ra, Rb and Rc
Since the body is in equilibrium and the forces are
concurrent ……
∑FX=0; Rf Cos600 - Rc Sin600 = 0 ………1
∑FY=0; Rf Sin600 + Rc Cos600 - W(100) = 0…...2
Rf=86.6N
Rc=50N
Since the body is in equilibrium and the forces are
concurrent ……
∑FX=0; -Rb sin600 - Rf Cos600 + Ra = 0 ………..…1
∑FY=0; Rb Cos600 - Rf Sin600 – W = 0…………..2
Copyright 2014 M K Chaitanya
Rb = 350N
Ra = 346.4N
21

22. Problem
Find T1, T2 , T3 and θ
Problem – 2D - Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
22

23. Problem
Find T1, T2 , T3 and θ
Problem solution:
FBD of A
FBD of B
Copyright 2014 M K Chaitanya
23

24. Problem solution
Since the body is in equilibrium and the forces are
concurrent ……
T1=48.8N
∑FY=0; T1 Cos350 - W(40N) = 0…...2
FBD of A
∑FX=0; T2 – T1Sin 350 = 0 ……….…1
T2=28.0N
Since the body is in equilibrium and the forces are
concurrent ……
∑FX=0; -T2 + T3Sin θ0 = 0 ……….…1
FBD of B
∑FY=0; T3 Cos θ0 - W(50N) = 0…...2
Copyright 2014 M K Chaitanya
T3=57.3N
θ=29.3N
24

25. Types of supports and reaction forces (2D)
Copyright 2014 M K Chaitanya
25

26. Problem
Determine the reactions at A and B
Problem – 2D - Non Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
26

27. Problem solution
Since the body is in equilibrium and the forces are general
forces then……
∑FX=0; Rax = 0 ……………………….…1
Rby=30N
∑FY=0; Ray + Rby - 40 = 0…...........2
Ray=10N
∑MA=0; (Rby*L) – 40*(3L/4) = 0……3
Rax=0N
Copyright 2014 M K Chaitanya
27

28. Problem
A man raises a 10 kg joist, of length 4 m, by pulling on a rope. Find
the tension in the rope and the reaction at A.
Since the body is in equilibrium then…….
∑FX=0; Rx – Tc*Cos200= 0 ……….…1
∑FY=0; Ry - Tc* Sin200 - W(98.1) = 0….........2
Tc=82N
Rx=77.1N
Ry=126.14N
∑MA=0; -(W*L/2) + (Tc*Cos200*4Sin450) –(Tc*Sin200*4*Cos450) = 0……3
Copyright 2014 M K Chaitanya
28

29. Problem
Determine the reaction at C and the reaction at E, Given P=200N
From the freebody diagram of AB .Since the body is in equilibrium then…… ……
∑FX=0; Rx + P*Cos300= 0 …………..…1
RC=150N
∑FY=0; Ry + Rc- PSin300 = 0…….........2
∑MA=0; (Rc* 2.44) - (PSin300* 3.66) = 0……….3
CONTINUES……..
Copyright 2014 M K Chaitanya
29

30. From the freebody diagram of DE .Since the body is in equilibrium then…… ……
∑FX=0; Rx - RE Sin600= 0 …………..…1
∑FY=0; Ry – RC+ RECos600 = 0…….........2
RE=100N
∑MD=0; (RC*1.22) - (RECos600 * 3.66) = 0……….3
Copyright 2014 M K Chaitanya
30

31. Problem
A roller weighting 2000N rests on a inclined bar weighting 800N as
shown in Fig. Assuming the weight of bar negligible, determine the
reactions at D and C and reaction in bar AB.
Problem – 2D – (Both Concurrent & Non Concurrent
- Equilibrium)
Copyright 2014 M K Chaitanya
31

32. Problem
FBD of Figure
Concurrent
Non Concurrent
Copyright 2014 M K Chaitanya
32

33. Problem
Equilibrium of Concurrent force system
From the free body diagram of ball .Since the body is in equilibrium then…… ……
∑FX=0; R1 – R2*Sin300= 0 …………..…1
R1=1154.7N
∑FY=0; R2 *Cos300 -2000 = 0…….........2
R2=2309.4N
CONTINUES……..
Copyright 2014 M K Chaitanya
33

34. Problem
Equilibrium of Non Concurrent force system
From the freed body diagram of ROD .Since the body is in equilibrium then…… ……
∑FX=0; -Hc + R2*Sin300= 0 …………..…1
∑FY=0; RD + Vc -R2*Cos300 - 800 = 0…….........2
∑MC=0; (RD* 5 Cos300) - (800* 2.5 Cos 300) - R2*2 = 0……….3
Copyright 2014 M K Chaitanya
Hc=1154.7N
Vc=1333.3N
RD=1466.7N
34

35. Method of approach to solve NON COPLANAR (3D) STATIC problems
Problem
3-D
Concurrent
Non Concurrent
Not equilibrium
Equilibrium
(Resultant)
(Unknowns)
--- --- --- -R = F1+F2+F3……
--- --R= 0
--- --- -- -F1+F2+F3….= 0
ΣFx=0
ΣFy=0
Not Equilibrium
Equilibrium
(Resultant)
(Unknowns)
--- -- -- -R= F1+F2+F3….
--- --- --- --M = M1+M2+M3....
--- --R= 0
--- --rOPͯ R = M
--- --M= 0
ΣFx=0 , ΣMx=0
ΣFz=0,
ΣFy=0, ΣMy=0
ΣFz=0, ΣMz=0
Copyright 2014 M K Chaitanya
35

36. Resultant of Concurrent Forces In 3D
R  FAB  FAC  FAD


R  FAB .

R  FAB .
AB
AC
AD
 FAC .
 FAD .
AB
AC
AD
AB
 FAC .


AC
 FAD .

R   Fx i +  Fy j +  Fz k
cos  x 
cos  y 
Copyright 2014 M K Chaitanya
cos  z 
 Fx
R
Fy
R
 Fz
R
36
AB

37. Problem
Determine the Resultant acting at A
Problem – 3D- Concurrent - Resultant
Copyright 2014 M K Chaitanya
37

38. Example:1
Determine the Resultant acting at A
R  Fab  Fac
Fab  FAB .


{-2i - 6 j  3 k}
Fab  840 *
Fac  FAC .
(-2)  ( 6 )  3
2
Magnitude of Resultant is
2
2


Fac  420 *
R  Fab  Fac
AB
AC
{3i - 6 j  2 k}
(3) 2  ( 6 2 )  2 2
R  - 60i - 1080j  480k
 (-60)2  (10802 )  4802  1183.3N
Copyright 2014 M K Chaitanya
38
.

39. R  - 60i - 1080j  480k
Magnitude of Resultant is
 (-60)2  (10802 )  4802  1183.3N
 60
Cos x 
; x  930
1183.3
 1080
Cos y 
; y  155.80
1183.3
480
Cos z 
; z  660
1183.3
Copyright 2014 M K Chaitanya
39

40. Resultant of Concurrent Forces In 3D
r
OP
RMO
Copyright 2014 M K Chaitanya
40

41. Problem
Determine the Resultant non concurrent of the
forces (3D)
Problem – 3D- Non Concurrent - Resultant
Copyright 2014 M K Chaitanya
41

42. Transfer all forces about O to get a
force and couple system
R   F  500k - 300k  200k - 50k
R  350k
M
M
M
O
 (r OA  50k )  (r OB  200k )  (r OC  300k )
O
 ((0.35j  0.5i)  50k )  (0.5i  200k )  ( 0.35j  300k )
O
 87.5i - 125j
Copyright 2014 M K Chaitanya
42

43. Reduce the force couple system to a single
force
r
OP
 R  MO
(x i  y j  z k)  (350k)  87.5i - 125j
x  0.375m, y  0.25m
Copyright 2014 M K Chaitanya
43

44. Problem
Given: A 1500N plate, as shown, is supported
by three cables and is in equilibrium.
Find: Tension in each of the cables.
Problem – 3D- Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
44

45. Equilibrium of 3D concurrent forces
--- --R= 0
--- --- -- -F1+F2+F3….= 0
ΣFx=0
ΣFy=0
ΣFz=0,
Copyright 2014 M K Chaitanya
45

46. y
W
FBD of Point A:
x
z
FAB FAC
FAD
The particle A is in equilibrium, hence
FAB  FAC  FAD  W  0
Copyright 2014 M K Chaitanya
46

47. F AB  FAB .


F AB  FAB *
FAC  FAC .
(-6)  (12 )  4
2
.
AC
{-4i - 12 j  6 k}
(-4)2  (12 2 )  (6) 2


AD
{6i - 12 j  4 k}
(6) 2  (12 2 )  (4) 2
W  1500j
Copyright 2014 M K Chaitanya
2


FAD  FAD *
{-6i - 12 j  4 k}
2
FAC  FAC *
FAD  FAD .
AB
47

48. FAB  FAC  FAD  W  0
Solving the three simultaneous equations gives
FAB = 858 N
FAC = 0 N
FAD = 858 N
Copyright 2014 M K Chaitanya
48

49. Problem
Example – 3D Equilibrium
Three cables are used to tether a balloon as shown. Determine the
vertical force P exerted by the balloon at A knowing that the tension in
cable AB is 60 N.
y
P
x
z
FAB FAC
FAD
FAB  FAC  FAD  P  0
Copyright 2014 M K Chaitanya
49

50. Types of supports and reaction forces (3D)
Copyright 2014 M K Chaitanya
50

51. Types of supports and reaction forces (3D)
Copyright 2014 M K Chaitanya
51

52. Problem
Given: Determine the reaction in the string CD and reactions at B. A ball and socket
joint at A
Problem – 3D- Non Concurrent - Equilibrium
Copyright 2014 M K Chaitanya
52

53. Equilibrium of 3D Non concurrent forces
--- --R= 0
--- --- -- -F1+F2+F3….= 0
--------R=0 =
M
--0
--- -- ----- ------ -F1+F2+F3….= 0
M1+M2+M3….= 0
ΣFx=0
ΣFy=0
ΣFx=0 ,
ΣFz=0,
ΣMx=0
ΣFy=0, ΣMy=0
ΣFz=0, ΣMz=0
Copyright 2014 M K Chaitanya
53

54. Problem Solution
Copyright 2014 M K Chaitanya
54

55. M 0
(r  T
A
1
CD
)  (r 2  2i )  (r 3  ( B y j  Bz k )  0
(6 j - 3k)  TCD
CD
 (6 j  2.5k)  2i  (6 j  4.5i)  ( B y j  Bz k )  0
CD
TCD  2.83kN
BY  4.06kN
BZ  0.417 kN
AX  3.05kN
AY  1.556kN
AZ  1.250kN
Copyright 2014 M K Chaitanya
55

56. References
•
•
•
•
•
•
•
•
•
•
•
•
Engg. Mechanics ,Timoshenko & Young.
2.Engg. Mechanics, R.K. Bansal , Laxmi publications
3.Engineering Mechanics,Fedinand.L.Singer , Harper – Collins.
4. Engineering Mechanics statics and dynamics, A Nelson, Mc Gra Hill publications
5. Engg. Mechanics Umesh Regl, Tayal.
6. Engineering Mechanics by N H Dubey
7. Engineering Mechanics , statics – J.L.Meriam, 6th Edn – Wiley India Pvt Ltd.
8. Engineering Mechanics , dynamics – J.L.Meriam, 6th Edn – Wiley India Pvt Ltd.
9. Mechanics For Engineers , statics - F.P.Beer & E.R.Johnston 5th Edn Mc Graw Hill
Publ.
10.Mechanics For Engineers, dynamics - F.P.Beer & E.R.Johnston – 5th Edn Mc
Graw Hill Publ.
11. www.google.com
12. http://nptel.iitm.ac.in/
Copyright 2014 M K Chaitanya
56

57. THANK YOU
Copyright 2014 M K Chaitanya
57