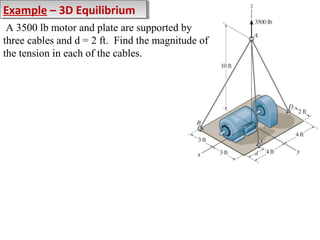
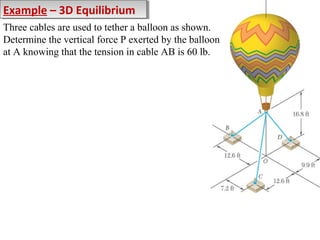
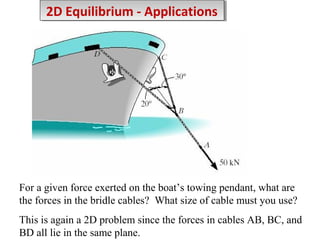
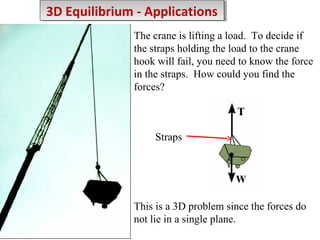
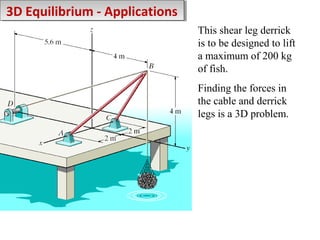
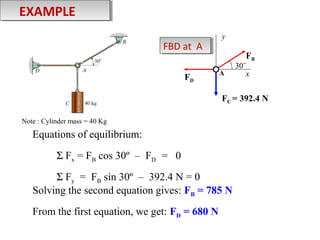
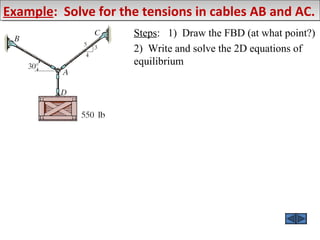
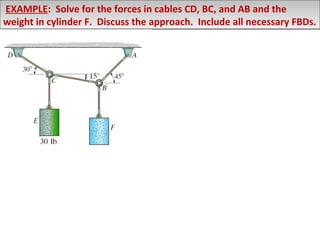
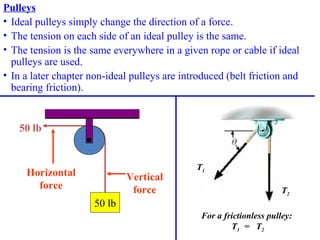
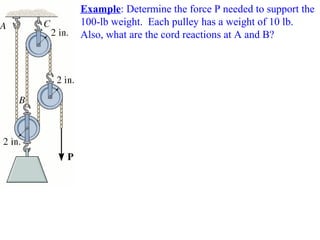
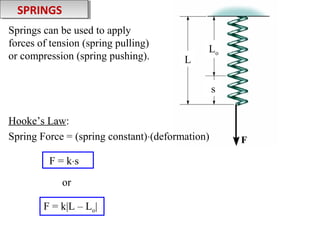
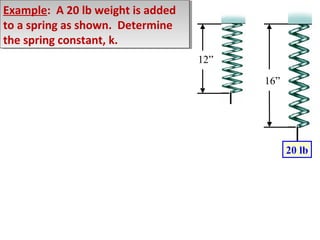
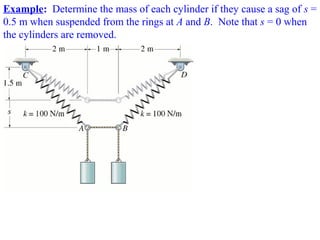
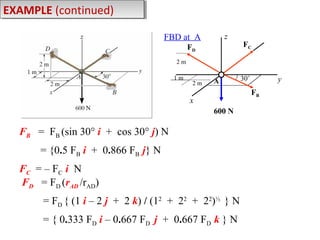
The document discusses equilibrium of particles and coplanar force systems. It has the following key points: 1) It introduces concepts of equilibrium, free body diagrams, and equations of equilibrium (scalar and vector forms) for solving 2D and 3D static equilibrium problems. 2) Examples are provided to demonstrate drawing free body diagrams and using the equations of equilibrium to solve for unknown forces in 2D and 3D systems involving cables, pulleys, springs, and other mechanics elements. 3) Procedures are outlined for setting up and solving static equilibrium problems involving both 2D coplanar and 3D non-coplanar force systems.

1. EQUILIBRIUM OF A PARTICLE, THE FREE-BODY
EQUILIBRIUM OF A PARTICLE, THE FREE-BODY
DIAGRAM & COPLANAR FORCE SYSTEMS
DIAGRAM & COPLANAR FORCE SYSTEMS
Ch. 3 Objectives:
Students will be able to :
a) Explore the concept of equilibrium
b) Draw a free body diagram (FBD), and,
c) Apply equations of equilibrium to solve a 2D problem.
d) Apply equations of equilibrium to solve a 3D problem.

2. EQUILIBRIUM OF A PARTICLE, THE FREE-BODY DIAGRAM &
EQUILIBRIUM OF A PARTICLE, THE FREE-BODY DIAGRAM &
COPLANAR FORCE SYSTEMS
COPLANAR FORCE SYSTEMS
Equilibrium
A key concept in statics is that of equilibrium. If an object is at rest, we
will assume that it is in equilibrium and that the sum of the forces
acting on the object equal zero.
Newton’s First Law of Physics: If the resultant force on a
particle is zero, the particle will remain at rest or will continue
at constant speed in a straight line.
Resultant of all
forces acting on a
particle is zero.
Equilibrium

3. EQUILIBRIUM OF A PARTICLE, THE FREE-BODY DIAGRAM &
EQUILIBRIUM OF A PARTICLE, THE FREE-BODY DIAGRAM &
COPLANAR FORCE SYSTEMS
COPLANAR FORCE SYSTEMS
Equilibrium
If an object is in equilibrium, then the resultant force acting on an object
equals zero. This is expressed as follows:
FR = ∑F = 0
(vector equation)
Some problems can be analyzed using only 2D, while others
require 3D.
Equations for 2D Equilibrium:
If a problem is analyzed using
2D, then the vector equation
above can be expressed as:
∑ Fx = 0 ∑ Fy = 0
(2D scalar equations)
Equations for 3D Equilibrium:
If a problem is analyzed using 3D,
then the vector equation above can
be expressed as:
∑F
x
=0
∑F
y
=0
(3D scalar equations)
∑F
z
=0

4. 2D Equilibrium -- Applications
2D Equilibrium Applications
Since the forces involved in supporting the spool lie in a plane, this is
essentially a 2D equilibrium problem. How would you find the forces in
cables AB and AC?

5. 2D Equilibrium -- Applications
2D Equilibrium Applications
For a given force exerted on the boat’s towing pendant, what are
the forces in the bridle cables? What size of cable must you use?
This is again a 2D problem since the forces in cables AB, BC, and
BD all lie in the same plane.

6. 3D Equilibrium -- Applications
3D Equilibrium Applications
The crane is lifting a load. To decide if
the straps holding the load to the crane
hook will fail, you need to know the force
in the straps. How could you find the
forces?
Straps
This is a 3D problem since the forces do
not lie in a single plane.

7. 3D Equilibrium -- Applications
3D Equilibrium Applications
This shear leg derrick
is to be designed to lift
a maximum of 200 kg
of fish.
Finding the forces in
the cable and derrick
legs is a 3D problem.

8. Coplanar Force Systems (2D Equilibrium) -- (Section 3.3)
Coplanar Force Systems (2D Equilibrium) (Section 3.3)
This is an example of a 2-D or
coplanar force system.
If the whole assembly is in
equilibrium, then particle A is
also in equilibrium.
To determine the tensions in
the cables for a given weight
of the cylinder, you need to
learn how to draw a free
body diagram and apply the
equations of equilibrium.

9. FREE BODY DIAGRAM (FBD)
FREE BODY DIAGRAM (FBD)
Free Body Diagrams are an important part of a course in Statics as
well as other courses in mechanics (Dynamics, Mechanics of
Materials, Fluid Mechanics, etc.,)
Free Body Diagram -- A drawing that shows all
Free Body Diagram A drawing that shows all
external forces acting on the particle.
external forces acting on the particle.
Why? -- It is key to being able to write the
Why? It is key to being able to write the
equations of equilibrium—which are used to
equations of equilibrium—which are used to
solve for the unknowns (usually forces or angles).
solve for the unknowns (usually forces or angles).

10. Procedure for drawing a Free Body Diagram (FBD)
Procedure for drawing a Free Body Diagram (FBD)
1. Imagine the particle to be isolated or cut free from its
surroundings.
2. Show all the forces that act on the particle.
Active forces: They want to move the particle.
Reactive forces: They tend to resist the motion.
3. Identify each force and show all known magnitudes and
directions. Show all unknown magnitudes and / or directions
as variables .
y
FBD at A
FD A
Area to be cut
or isolated
Note : Cylinder mass = 40 Kg
FB
A
30˚
x
FC = 392.4 N (What is this?)

11. EQUATIONS OF 2-D EQUILIBRIUM
EQUATIONS OF 2-D EQUILIBRIUM
FBD at A
FD A
y
A
FB
30˚
x
A
FC = 392.4 N
Since particle A is in equilibrium, the
net force at A is zero.
So FB + FC + FD = 0
or Σ F = 0
FBD at A
In general, for a particle in equilibrium,
Σ F = 0 or
Σ Fx i + Σ Fy j = 0 = 0 i + 0 j
(a vector equation)
Or, written in a scalar form,
ΣFx = 0 and Σ Fy = 0
These are two scalar equations of equilibrium.
They can be used to solve for up to two unknowns.

12. EXAMPLE
EXAMPLE
FBD at A
FBD at A
FD A
y
A
30˚
FB
x
FC = 392.4 N
Note : Cylinder mass = 40 Kg
Equations of equilibrium:
Σ Fx = FB cos 30º – FD = 0
Σ Fy = FB sin 30º – 392.4 N = 0
Solving the second equation gives: FB = 785 N
From the first equation, we get: FD = 680 N

13. Example: Solve for the tensions in cables AB and AC.
Example: Solve for the tensions in cables AB and AC.
Steps: 1) Draw the FBD (at what point?)
2) Write and solve the 2D equations of
equilibrium

14. EXAMPLE: Solve for the forces in cables CD, BC, and AB and the
EXAMPLE: Solve for the forces in cables CD, BC, and AB and the
weight in cylinder F. Discuss the approach. Include all necessary FBDs.
weight in cylinder F. Discuss the approach. Include all necessary FBDs.

15. Pulleys
• Ideal pulleys simply change the direction of a force.
• The tension on each side of an ideal pulley is the same.
• The tension is the same everywhere in a given rope or cable if ideal
pulleys are used.
• In a later chapter non-ideal pulleys are introduced (belt friction and
bearing friction).
50 lb
Horizontal
force
Vertical
force
50 lb
T1
T2
T2
For a frictionless pulley:
T1 = T 2

16. Example - Determine the tension T required to
support the 100 lb block shown below.

17. Example: Determine the force P needed to support the
100-lb weight. Each pulley has a weight of 10 lb.
Also, what are the cord reactions at A and B?

18. Example: A 350-lb load is supported by the
rope-and-pulley arrangement shown.
Knowing that α = 35°, determine the angle β
and the force P.

19. SPRINGS
SPRINGS
Springs can be used to apply
forces of tension (spring pulling)
or compression (spring pushing).
L
Lo
s
Hooke’s Law:
Spring Force = (spring constant)⋅(deformation)
F = k⋅s
or
F = k|L – Lo|

20. Example: A 20 lb weight is added
Example: A 20 lb weight is added
to a spring as shown. Determine
to a spring as shown. Determine
the spring constant, k.
the spring constant, k.
12”
16”
20 lb

21. Example: Determine the mass of each cylinder if they cause a sag of s =
0.5 m when suspended from the rings at A and B. Note that s = 0 when
the cylinders are removed.

22. THREE-DIMENSIONAL FORCE SYSTEMS
THREE-DIMENSIONAL FORCE SYSTEMS
Recall that with 3D problems we will use three equations of equilibrium.
∑F
x
=0
∑F
y
=0
Also recall from the last chapter that
3D forces may be specified in
different ways, including:
1) With coordinate direction angles
(α, β, and γ),
2)With angles of projection onto a
plane,
3)With distances. When distances are
specified, we typically express the
force in Cartesian vector form using
position vectors as follows:
∑F
z
=0

23. Example – 3D Equilibrium
Example – 3D Equilibrium
Given: A 600 N load is supported
by three cords with the
geometry as shown.
Find: The tension in cords AB,
AC and AD.
Plan:
1) Draw a free body diagram of Point A. Let the unknown force
magnitudes be FB, FC, FD .
2) Represent each force in the Cartesian vector form.
3) Apply equilibrium equations to solve for the three unknowns.

24. EXAMPLE (continued)
EXAMPLE (continued)
z
FBD at A
FD
FC
2m
1m
2m
A
30˚
y
FB
x
600 N
FB = FB (sin 30° i + cos 30° j) N
= {0.5 FB i + 0.866 FB j} N
FC = – FC i N
FD = FD (rAD /rAD)
= FD { (1 i – 2 j + 2 k) / (12 + 22 + 22)½ } N
= { 0.333 FD i – 0.667 FD j + 0.667 FD k } N

25. EXAMPLE (continued)
EXAMPLE (continued)
Now equate the respective i , j , k
components to zero.
∑ Fx = 0.5 FB – FC + 0.333 FD = 0
∑ Fy = 0.866 FB – 0.667 FD = 0
FBD at A
FD
1m
y
2m
FB = 693 N
A
30˚
FB
x
Solving the three simultaneous equations yields
FD = 900 N
FC
2m
∑ Fz = 0.667 FD – 600 = 0
FC = 646 N
z
600 N

26. Example – 3D Equilibrium
Example – 3D Equilibrium
A 3500 lb motor and plate are supported by
three cables and d = 2 ft. Find the magnitude of
the tension in each of the cables.

27. Example – 3D Equilibrium
Example – 3D Equilibrium
Three cables are used to tether a balloon as shown.
Determine the vertical force P exerted by the balloon
at A knowing that the tension in cable AB is 60 lb.