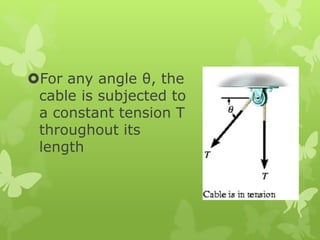
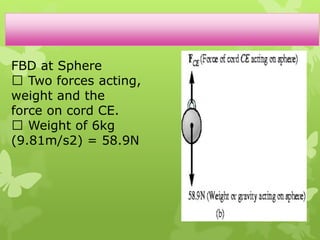
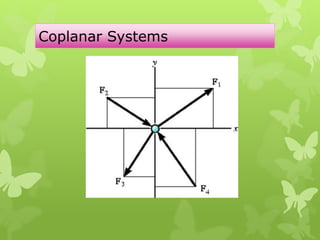
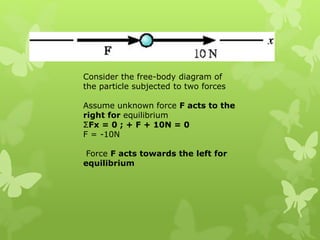
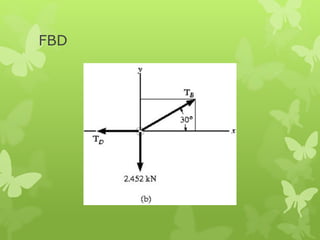
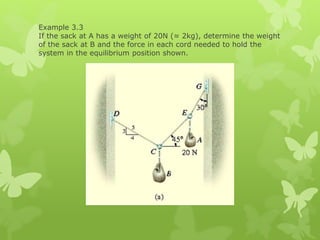
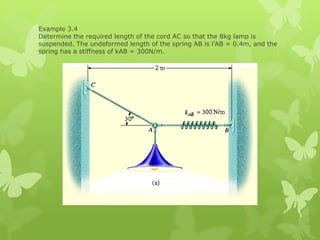
This chapter discusses particle equilibrium using free-body diagrams and equations of equilibrium. It introduces the concept of a free-body diagram to represent all unknown forces acting on a particle. Equilibrium requires the vector sum of all forces (ΣF) to equal zero. For coplanar systems, this is resolved into scalar equations with the x and y force components summing to zero. Examples show using free-body diagrams and equations to solve for tensions in cables and springs for systems in equilibrium.

1. JJ205
ENGINEERING MECHANICS
CHAPTER 3
EQUILIBRIUM OF PARTICLE
PREPARED BY:
AMRAN BIN AWANG @ MUDA
DEPARTMENT OF MECHANICAL ENGINEERING

2. CHAPTER OBJECTIVES
 To introduce the concept of the free-body diagram for a
particle.
 To show how to solve particle equilibrium problems using
the equations of equilibrium.

3. Chapter Outline
 Condition for the Equilibrium of a Particle
 The Free-Body Diagram
 Coplanar Systems

4. CONDITION FOR THE EQUILIBRIUM
OF A PARTICLE
Particle at equilibrium if
- At rest
-Moving at constant a constant velocity
Newton’s first law of motion
ΣF = 0
where ΣF is the vector sum of all the
forces acting on the particle

5. Newton’s second law of motion
ΣF = ma
When the force fulfill Newton's first law of motion,
ma = 0
a = 0
therefore, the particle is moving in constant velocity or at
rest

6. The Free-Body Diagram
 Best representation of all the unknownforces (ΣF)
which acts on a body
 A sketch showing the particle “free” from the
surroundings with all the forces acting on it
 Consider two common connections in this subject
 Spring
 Cables and Pulleys

7. Spring
 Linear elastic spring: change in length is directly
proportional to the force acting on it
 - spring constant or stiffness k:
 defines the elasticity of the spring
 - Magnitude of force when spring is elongated or
compressed
 F = ks

8.  where s is determined from the difference in spring’s deformed
length l and its undeformed length lo
 s = l - lo
 - If s is positive, F “pull”
onto the spring
 - If s is negative, F “push”
onto the spring

9. EXAMPLE
 Given lo = 0.4m and k = 500N/m
To stretch it until l = 0.6m, A force, F = ks
=(500N/m)(0.6m – 0.4m) = 100N is needed
To compress it until l = 0.2m,
 A force, F = ks
=(500N/m)(0.2m – 0.4m)
= -100N is needed

10. - Cables (or cords) are assumed to
have
negligible weight and they cannot
stretch
-A cable only support tension or
pulling force
- Tension always acts in the
direction of the cable
- Tension force in a continuous
cable must have a constant
magnitude for equilibrium
Cables and Pulley

11. For any angle θ, the
cable is subjected to
a constant tension T
throughout its
length

12. 1. Draw outlined shape
• Isolate particle from its surroundings
2. Show all the forces
• Indicate all the forces
• active forces: set the particle in motion
• Reactive forces: result of constraints and
supports that tend to prevent motion
Procedure for Drawing a
FBD

13. 3. Identify each forces
 - Known forces should be labeled with proper magnitude
and direction
 - Letters are used to represent magnitude and directions
of unknown forces

14.  A spool is having a weight W
which is suspended from the
crane bottom
 Consider FBD at A since these
forces act on the ring
 Cables AD exert a resultant
force of W on the ring
 Condition of equilibrium is
used to obtained TB and TC

15.  Each term must be expressed in
the same units
 Eg: s = vt + ½ at2 where s is
position in meters (m), t is time
in seconds (s), v is velocity in
m/s and a is acceleration in m/s2
 Regardless of how the equation
is evaluated, it maintains its
dimensional homogeneity
 All the terms of an equation can
be replaced by a consistent set
of units, that can be used as a
partial check for algebraic
manipulations of an equation

16.  The bucket is held in
 equilibrium by the cable
 Force in the cable =
 weight of the bucket
 Isolate the bucket for
 FBD
 Two forces acting on
 the bucket, weight W
 and force T of the cable
 Resultant of forces = 0
 W = T

17. Example 3.1
The sphere has a mass
of 6kg and is
supported. Draw a
free-body diagram of
the
sphere, the cord
CE and the knot at C.

18. FBD at Sphere
Two forces acting,
weight and the
force on cord CE.
Weight of 6kg
(9.81m/s2) = 58.9N

19. Solution
Cord CE
Two forces acting, force
of the sphere and force
of the knot
Newton’s Third Law: FCE
is equal but opposite
FCE and FEC pull the cord
in tension
For equilibrium, FCE =
FEC

20.  FBD at Knot
 Three forces acting, force by cord CBA, cord CE
 and spring CD
 Important to know that
 the weight of the sphere
 does not act directly on
 the knot but subjected to
 by the cord CE

21. Coplanar Systems
 A particle is subjected to coplanar forces in
 the x-y plane
 Resolve into i and j components for
 equilibrium
 ΣFx = 0
 ΣFy = 0
 Scalar equations of equilibrium
 require that the algebraic sum
 of the x and y components to
 equal o zero

22. Coplanar Systems

23. Scalar Notation
 Sense of direction = an algebraic sign that corresponds
to the arrowhead direction of the component along each
axis
 For unknown magnitude, assume arrowhead sense of
the force
 Since magnitude of the force is always positive, if the
scalar is negative, the force is acting in the opposite
direction

24. Consider the free-body diagram of
the particle subjected to two forces
Assume unknown force F acts to the
right for equilibrium
ΣFx = 0 ; + F + 10N = 0
F = -10N
Force F acts towards the left for
equilibrium

25.  The chain exerts three forces
on the ring at A.
 The ring will not move, or will
move with constant velocity,
provided the summation of the
forces along the y axis is zero
 With any force known, the
magnitude of other two forces
are found by equations of
equilibrium

26. Example 3.2
Determine the tension in cables AB and AD for equilibrium
of the 250kg engine.

27. FBD

28.  Solution
 +→ ΣFx = 0;
 +↑ ΣFy = 0;
 Solving,
 TB = 4.90kN
 TD = 4.25kN
 *Note: Neglect the weights of the cables since they
 are small compared to the weight of the engine

29. Example 3.3
If the sack at A has a weight of 20N (≈ 2kg), determine the weight
of the sack at B and the force in each cord needed to hold the
system in the equilibrium position shown.

30. Example 3.4
Determine the required length of the cord AC so that the 8kg lamp is
suspended. The undeformed length of the spring AB is l’AB = 0.4m, and the
spring has a stiffness of kAB = 300N/m.

31. Chapter Summary
Two Dimensional
 Two scalars equations ΣFx = 0 and ΣFy =
 0 is applied to x, y coordinate system
 If the solution is negative, the sense of
 the force is opposite to that shown on
 the FBD.
 If problem involves a linear spring,
 stretch or compression can be related to
 force by
 F = ks