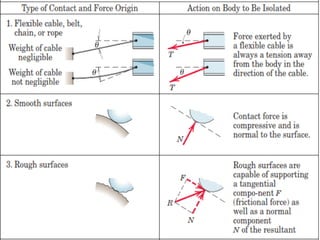
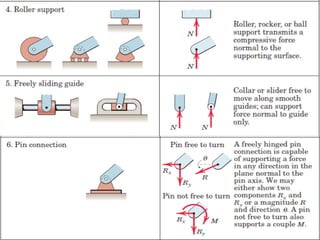
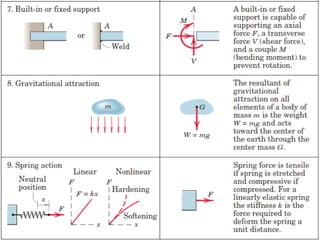
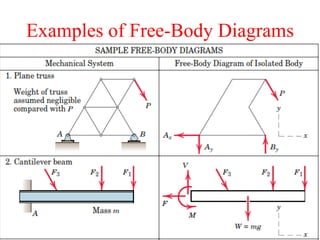
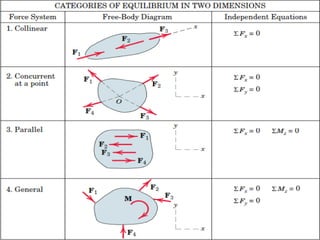
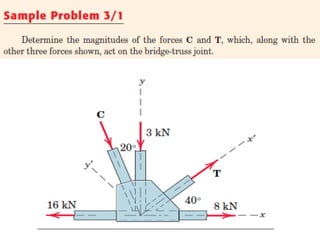
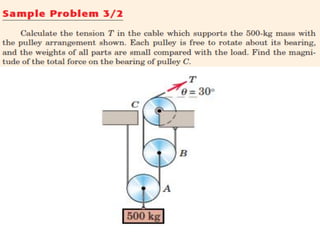
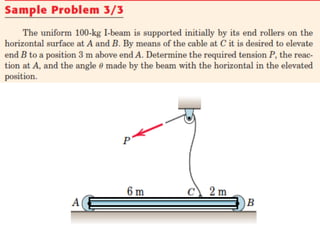
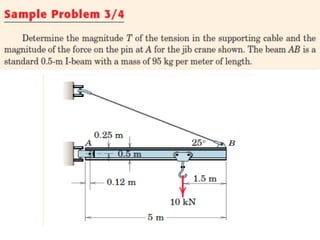
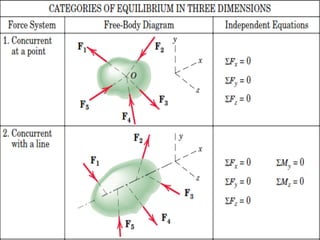
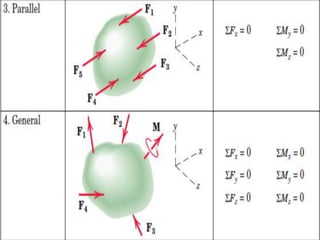
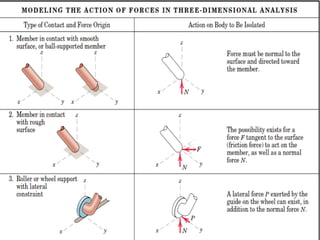
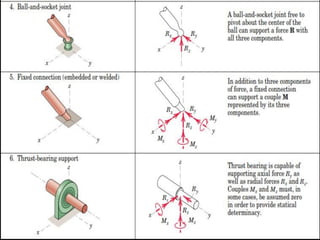
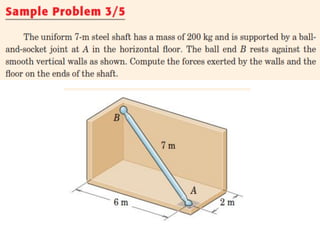
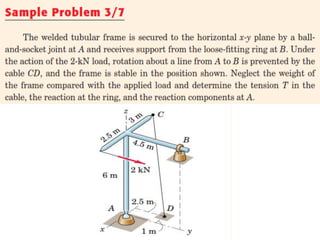
This document provides an introduction to the concept of equilibrium in statics. It discusses how to isolate a mechanical system and draw a free body diagram showing all external forces acting on it. For equilibrium in two dimensions, the forces must sum to zero in both the x and y directions. In three dimensions, six equations are required - the forces and moments must sum to zero in the x, y, and z directions as well as around each axis. Examples are given of two-force and three-force members in equilibrium. The document also defines statically determinate and indeterminate bodies.

1. EQUILIBRIUM
SECTION A: EQUILIBRIUM IN TWO
DIMENSIONS
• System Isolation and Free Body Diagram
•Equilibrium Conditions

2. INTRODUCTION
Statics deals primarily with the description of the force conditions
necessary and sufficient to maintain the equilibrium of engineering
structures. In this chapter we will form the basis for solving problems
in both STATICS and DYNAMICS
Continual use of concepts like FORCES, MOMENTS, COUPLES
and RESULTANTS as we apply the principles of EQUILIBRIUM
A body is said to be in equilibrium if the resultant of all forces
acting on it is ZERO
Equations shown on the next slide (conditions necessary and
sufficient for equilibrium)

4. SYSTEM ISOLATION AND THE FREE BODY
DIAGRAM
Basic Idea
To analyze and represent clearly and
completely all forces acting on the body
Mechanical System
Defined as a body or group of bodies which can
be conceptually isolated from all other bodies. A
system may be a single body or a combination
of connected bodies.

5. Free Body Diagram (FBD)
– Is a diagrammatic representation of the isolated system
treated as a single body.
– Shows all forces applied to the system by mechanical
contact with other bodies which are imagined to be
removed
– If appreciable body forces are present, such as
GRAVITATIONAL or MAGNETIC ATTRACTION,
then these forces must be shown on the FBD
– Is the most important single step in the solution of
problems in mechanics

6. BASIC CHARACTERISTICS OF FORCE
• Need to be recalled before drawing a FBD
vector properties of force
can be applied either by direct physical
contact or by remote action
Can either be internal or external to the
system under consideration
concentrated or distributed forces
principle of transmissibility (Sliding
Vectors)

7. MODELLING THE ACTION OF FORCES
Common types of force application on mechanical
systems for analysis in two dimensions.
Newton’s third law to be observed
Flexible cable, belt, chain, rope/ Smooth surfaces/
Rough surfaces/ Roller support/ Freely sliding
guide/ Pin connection/ Built-in or fixed support/
Gravitational attraction/ Spring action

11. Construction of Free-Body Diagrams
1. Decide which system to isolate. The system chosen
should usually involve one or more of the desired
unknown quantities
2. Isolate the chosen system by drawing a diagram
which represents its complete external boundary.
This step is often the most crucial of all.
3. Identify all forces which act on the isolated system
as applied by the removed contacting and attracting
bodies, and represent them in their proper positions
on the diagram of the isolated system. Include body
forces such as weights, where appreciable.

12. Construction of Free-Body
Diagrams
4. Show the choice of coordinate axes directly on
the diagram. Pertinent dimensions may also be
represented for convenience
Note that the FBD serves the purpose of
focusing attention on the action of external
forces.

13. Examples of Free-Body Diagrams

15. FREE BODY DIAGRAM EXERCISES

16. EQUILIBRIUM CONDITIONS

23. SECTION B: EQUILIBRIUM IN THREE
DIMENSIONS

24. 3-D Equilibrium
For general 3-D body, six scalar equations required to
express equilibrium
Equations can be solved for at most 6 unknowns
which generally are reactions
Scalar equations conveniently obtained from vector
equations of equilibrium-right handed coordinate
system

25. Free Body Diagram
• In three dimensions the free-body diagram
serves the same essential purpose as it does in
two dimensions and should always be drawn.

26. Categories of Equilibrium

33. Two- and Three-Force Members
• Two frequently occurring equilibrium
situations.
• The first situation is the equilibrium of a
body under the action of two forces only.
Two examples are shown in Fig. 3/4, and
we see that for such a two-force member
to be in equilibrium, the forces must be
equal, opposite, and collinear.
• The shape of the member does not affect
this simple requirement. In the
illustrations cited, we consider the
weights of the members to be negligible
compared with the applied force

34. • The second situation is a three-force
member, which is a body under the
action of three forces, Fig. 3/5a. We
see that equilibrium requires the
lines of action of the three forces to
be concurrent.
• If they were not concurrent, then
one of the forces would exert a
resultant moment about the point of
intersection of the other two, which
would violate the requirement of
zero moment about every point. The
only exception occurs when the
three forces are parallel. In this case
we may consider the point of
concurrency to be at infinity.

35. A rigid body, or rigid combination of elements treated as a
single body, which possesses more external supports or
constraints than are necessary to maintain an equilibrium
position is called statically indeterminate.
Supports which can be removed without destroying the
equilibrium condition of the body are said to be redundant.
On the other hand, bodies which are supported by the minimum
number of constraints necessary to ensure an equilibrium
configuration are called statically determinate, and for such
bodies the equilibrium equations are sufficient to determine the
unknown external forces.
STATICALLY DETERMINATE AND
INDETERMINATE BODIES