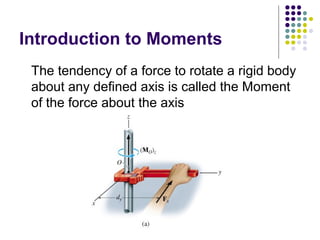
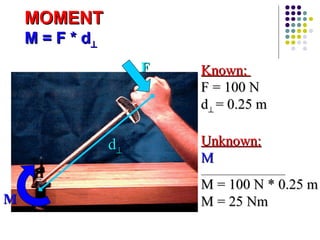
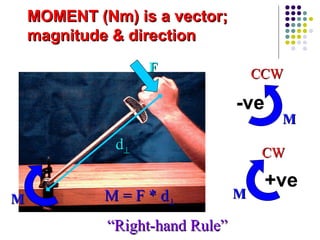
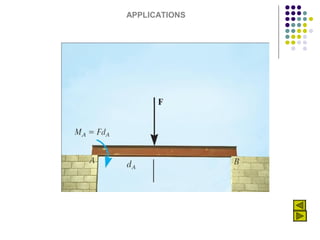
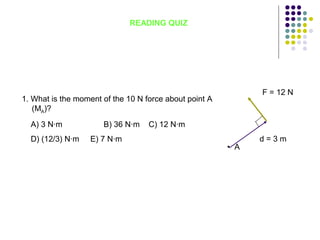
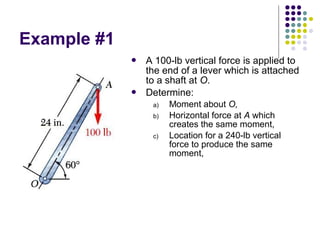
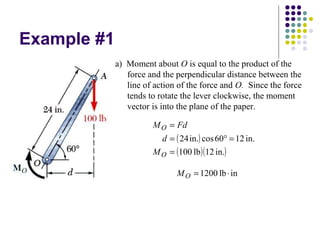
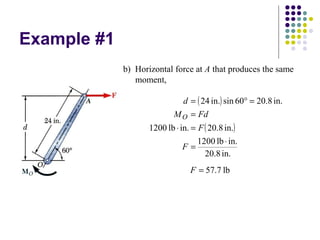
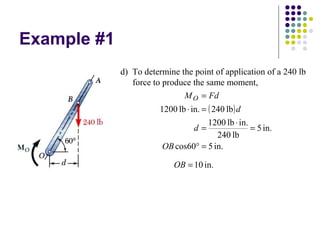
The document discusses moments, which are the tendency of a force to cause rotation about an axis. It defines key terms like moment, moment arm, and how to calculate moment using the equation: Moment = Force x Perpendicular Distance. It also covers units of moment, properties like sense of direction, and applications like Varignon's theorem for resolving forces. An example problem is worked through to find the moment created by different forces and placements.

1. BY: ENGR:MUNIR
AHMED MAHAR
Moment

2. Introduction to Moments
The tendency of a force to rotate a rigid body
about any defined axis is called the Moment
of the force about the axis

3. Causes of MotionCauses of Motion
M = F * dM = F * d⊥⊥
MOMENT (N*m): cause of angular rotationMOMENT (N*m): cause of angular rotation
Force (N) applied a perpendicular distance (m)
from the axis of rotation.
dd⊥⊥
MM FF

4. Moment ArmMoment Arm
dd⊥⊥ (m)(m)
Perpendicular distance from the point ofPerpendicular distance from the point of
force application to the axis of rotationforce application to the axis of rotation
dd⊥⊥
dd⊥⊥ dd⊥⊥

5. MOMENTMOMENT
M = F * dM = F * d⊥⊥
FF
dd⊥⊥
MM
Known:Known:
F = 100 NF = 100 N
dd⊥⊥ = 0.25 m= 0.25 m
Unknown:Unknown:
MM
__________________________________________
M = 100 N * 0.25 mM = 100 N * 0.25 m
M = 25 NmM = 25 Nm

6. MOMENT (Nm) is a vector;MOMENT (Nm) is a vector;
magnitude & directionmagnitude & direction
FF
dd⊥⊥
MM MM
MM
+-ve
+ve
CCWCCW
CWCW
M = F * dM = F * d⊥⊥
““Right-hand Rule”Right-hand Rule”

7. Moment of a Force
 It is a turning effect produced by a force on a
body, on which it acts. The moment of force is
equal to the product of force and the
perpendicular distance of a point, about which
moment is required and line of action of the
force.
Mathematically
M= F x D
Where

8. F = Force acting on the body
D= Perpendicular distance between the
point about which the moment is
required and the line of action of
force.

9. Units of a Moment
 The units of a Moment are:
 N·m in the SI system
 ft·lbs or in·lbs in the FPS system

10. APPLICATIONS

11. Properties of a Moment
 Moments not only have
a magnitude, they also
have a sense to them.
 The sense of a moment
is clockwise or counter-
clockwise depending
on which way it will
tend to make the object
rotate

12. Varignon’s Theorem
 The moment of a force about a point is equal
to the sum of moments of the components of
the force about the point:
 This means that resolving or replacing forces
with their resultant force will not affect the
moment on the object being analyzed

13. READING QUIZ
1. What is the moment of the 10 N force about point A
(MA)?
A) 3 N·m B) 36 N·m C) 12 N·m
D) (12/3) N·m E) 7 N·m
• A
d = 3 m
F = 12 N

14. Example #1
 A 100-lb vertical force is applied to
the end of a lever which is attached
to a shaft at O.
 Determine:
a) Moment about O,
b) Horizontal force at A which
creates the same moment,
c) Location for a 240-lb vertical
force to produce the same
moment,

15. Example #1
( )
( )( )in.12lb100
in.1260cosin.24
=
=°=
=
O
O
M
d
FdM
a) Moment about O is equal to the product of the
force and the perpendicular distance between the
line of action of the force and O. Since the force
tends to rotate the lever clockwise, the moment
vector is into the plane of the paper.
inlb1200 ⋅=OM

16. Example #1
( )
( )
in.8.20
in.lb1200
in.8.20in.lb1200
in.8.2060sinin.24
⋅
=
=⋅
=
=°=
F
F
FdM
d
O
b) Horizontal force at A that produces the same
moment,
lb7.57=F

17. Example #1
( )
in.5cos60
in.5
lb402
in.lb1200
lb240in.lb1200
=°
=
⋅
=
=⋅
=
OB
d
d
FdMO
d) To determine the point of application of a 240 lb
force to produce the same moment,
in.10=OB