The document discusses basic principles of statics and structural design. It covers: 1) Statics deals with forces on bodies at rest, while dynamics deals with moving bodies. Statics is used to analyze structural systems and ensure strength, stiffness, and stability. 2) Structural design involves preliminary design stages using experience and intuition, followed by detailed analysis and load estimations based on statics principles. 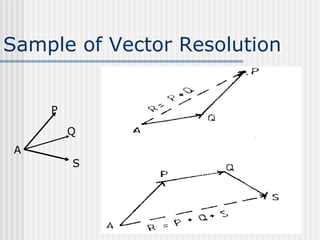3) Static equilibrium equations must be satisfied for coplanar forces. Systems can be determinate, allowing determination of specific unknowns, or indeterminate.

1. Basic principles of statics
 Structural system is concerned with
the strength, stiffness and stability
of structures such as buildings,
dams, bridges and retaining walls.
 Although a building is constructed
from the foundation upwards, the
designer usually starts designing
from the top, the roof and works his
way downwards.

2. Stages of Structural Design
 2 distinct stages in structural design.
 1st
experience, intuition and knowledge, an
imaginative choice of preliminary design in terms of
layout, materials and erection methods.
 2nd
is the estimation of the various forms of loading
are made
 3rd
the chosen design is subjected to detailed
analysis based on the principles of statics.
 Statics = branch of mechanics & deals with forces on
bodies, which are 'at rest' (static equilibrium).
Another branch, dynamics, deals with moving
bodies, such as parts of machines

3. Newton’s Laws of Motion

4. Newton's First Law of Motion
 An object at rest
tends to stay at
rest and an object
in motion tends to
stay in motion with
the same speed
and in the same
direction
unless acted upon by
.

5. Newton’s Second Law
 Consider another
example involving
balanced forces - a
person standing upon
the ground. There are
two forces acting upon
the person. The force
of gravity exerts a
downward force. The
floor of the floor
exerts an upward
force.

6. Static Equilibrium
Forces acting in one plane (i.e., coplanar)
and in equilibrium must satisfy one of the
following sets of conditions:
Σ Fx
=0 Σ Fx
=0 Σ Fy
=0 Σ Ma
=0
Σ Fy
=0 or Σ Ma
=0 or Σ Ma
=0 or Σ Mb
=0
Σ Ma
=0 Σ Mb
=0 Σ Mb
=0 Σ Mc
=0
where F refers to forces and M refers to
moments of forces.

7. Static Determinacy
 If a body is in equilibrium under the
action of coplanar forces, the equations of
statics above must apply.
 In general then, 3 independent unknowns
can be determined from the 3 equations.
 But, if applied and reaction forces are
parallel (i.e., in one direction only) only 2
separate equations obtain and then only
two unknowns can be determined. Such
systems of forces are said to be statically
determinate.

8. Force
 A force is any cause which tends to alter the state or
rest of a body or its state of uniform motion in a
straight line.
 A force can be a quantitatively as the product of the
mass of the body, which the force is acting on, and
the acceleration of the force.
 F = ma where
F = applied force
m= mass of the body ( kg)
a = acceleration caused by the force (m/s2
)
 The Sl units for force are therefore kg m/s2
which is
designated a Newton (N). The following multiples are
often used:
 1kN = 1,000N, 1MN = 1,000,000N

9. Gravitational Force
All objects on earth tend to accelerate toward the center of the
earth due to gravitational attraction, hence the force of gravitation
acting on a body with the mass (m) is the product of the mass
and the acceleration due to gravity (g), which has a magnitude of
9.81 m/s².
F = mg = vρ g where:
F = force (N)
m= mass ( kg)
g = acceleration due to gravity (9.8m/s²)
v = volume (m³)
ρ = density ( kg/m³)

10. Vector
 Most forces have magnitude and direction
and can be shown as a vector.
 Its point of application must also be
specified.
 A vector is illustrated by a line, whose
length is proportional to the magnitude to
some scale and an arrow which shows
the direction.

11. Vector Addition
 The sum of 2 or more vectors is called the resultant.
The resultant of 2 concurrent vectors is obtained by
constructing a diagram of the two vectors.
 The vectors to be added are arranged in tip-to-tail
fashion. Where 3 or more vectors are to be added
they can be arranged in the same manner and this is
called a polygon. A line drawn to close the triangle or
polygon (from start to finishing point) forms the
resultant vector.
 The subtraction of a vector is defined as the addition
of the corresponding negative vector.

12. Illustration of Vector Addition

13. Vector Resolution
 In analysis and calculation it is often
convenient to consider the effects of a force
in other directions than that of the force
itself, especially along the Cartesian (xx-yy)
axes. The force effects along these axes are
called vector components and are obtained
by reversing the vector addition method.
 Fy
is the component of F in the 'y' direction Fy
= F sin θ
 Fx
is the component of F in the 'x' direction Fx
= F cos θ

14. Sample of Vector Resolution
P
Q
S
A

15. Concurrent Coplanar Forces
 Concurrent Forces have their line of action
meeting at one point
 Coplanar forces lie in the same plane
 Non-coplanar forces have to be related to a
 3 dimensional space and require 2 items of
directional data together with the magnitude.
 2 Coplanar nonparallel forces will always be
concurrent.

16. Elements of Coplanar Force
Resolution
 There are many ways in which forces can
be manipulated.
 It is often easier to work with a large,
complicated system of forces by reducing
it an ever decreasing number of smaller
problems.
 This is called the "resolution" of forces or
force systems.
 This is one way to simplify what may
otherwise seem to be an impossible
system of forces acting on a body.

17. Coplanar Force Systems
 Certain systems of forces are easier
to resolve than others.
 Coplanar force systems have all the
forces acting in in one plane. They
may be concurrent, parallel, non-
concurrent or non-parallel. All of
these systems can be resolved by
using graphic statics or algebra.

18. Concurrent Coplanar
Force System
 A concurrent coplanar force system is a system
of two or more forces whose lines of action ALL
intersect at a common point. However, all of the
individual vectors might not actually be in
contact with the common point. These are the
most simple force systems to resolve with any
one of many graphical or algebraic options.

19. Parallel -Coplanar Force System
 A parallel coplanar force system consists
of two or more forces whose lines of
action are ALL parallel. This is commonly
the situation when simple beams are
analyzed under gravity loads. These can
be solved graphically, but are combined
most easily using algebraic methods.

20. Non-concurrent and Non-parallel
System
 A non-concurrent
and non-parallel
system consists of a
number of vectors
that do not meet at a
single point and none
of them are parallel.
These systems are
essentially a jumble of
forces that require
considerable care to
resolve.

21. Concurrent & Parallel Forces