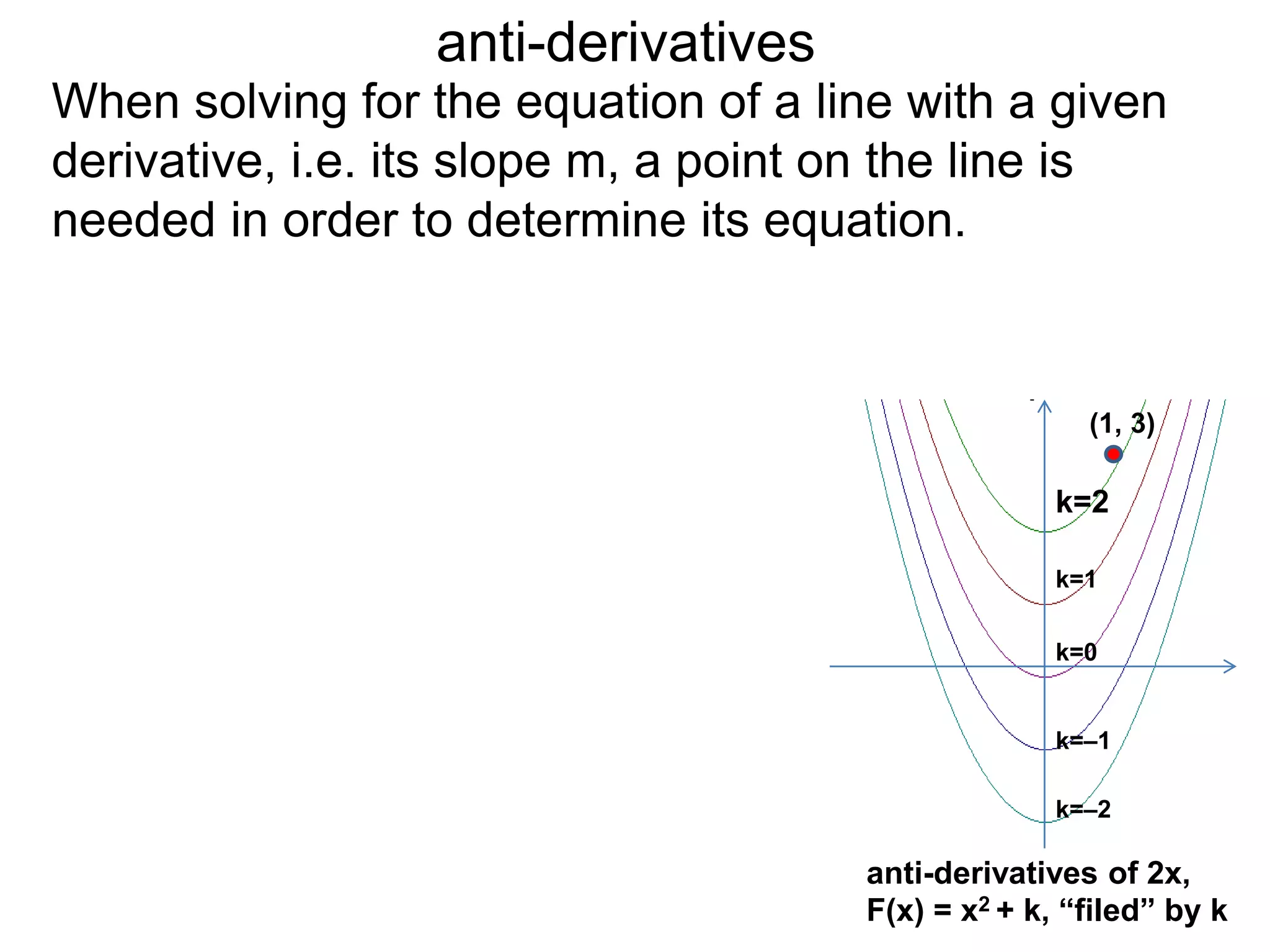
The document discusses anti-derivatives and integration. It defines an anti-derivative F(x) of a function f(x) as any function whose derivative is f(x). It also calls F(x) the indefinite integral of f(x). The document outlines basic integration rules for adding, subtracting and multiplying terms by constants when taking integrals. It provides examples of integrals of common functions and explains that the integration constant k positions the graph of the anti-derivative F(x).

1. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives

2. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives
We also call F(x) “the (indefinite) integral of f(x)”.

3. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives
We write this as
∫f(x) dxF(x) =
We also call F(x) “the (indefinite) integral of f(x)”.

4. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives
We write this as
∫f(x) dxF(x) =
We also call F(x) “the (indefinite) integral of f(x)”.
∫0 dx = k
Fact: The anti-derivatives of the function f(x) = 0
are exactly all the constant functions F(x) = k or that

5. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives
We write this as
∫f(x) dxF(x) =
We also call F(x) “the (indefinite) integral of f(x)”.
Remarks
I. There is only one derivative for any f(x) but the
“anti-derivatives” of f(x) is a set of functions.
∫0 dx = k
Fact: The anti-derivatives of the function f(x) = 0
are exactly all the constant functions F(x) = k or that

6. We say F(x) is an anti-derivative of f(x) if F'(x) = f(x).
anti-derivatives
We write this as
∫f(x) dx
∫0 dx = k
F(x) =
We also call F(x) “the (indefinite) integral of f(x)”.
Remarks
I. There is only one derivative for any f(x) but the
“anti-derivatives” of f(x) is a set of functions.
II. Any two anti-derivatives of f(x) must differ by a
constant. Hence if F'(x) = G'(x) then F(x) = G(x) + k
for some constant k.
Fact: The anti-derivatives of the function f(x) = 0
are exactly all the constant functions F(x) = k or that

7. The procedure of finding the anti-derivatives is called
“integration”.
anti-derivatives

8. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
Basic Integration Rules

9. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g.
Let f, g, F, G and that F' = f and G' = g,
Basic Integration Rules

10. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
Basic Integration Rules

11. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
and we say that we can “integrate term by term”.
Basic Integration Rules

12. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
For any constant c, (c*F) ' = c*F'= c*f,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
and we say that we can “integrate term by term”.
Basic Integration Rules

13. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
For any constant c, (c*F) ' = c*F'= c*f, so in integrals,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
∫cf dx = c∫f dx
and we say that we can “integrate term by term”.
Basic Integration Rules

14. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
For any constant c, (c*F) ' = c*F'= c*f, so in integrals,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
∫cf dx = c∫f dx
and we say that we can “integrate term by term”.
We say that we can “pull out the constant multiple.”
Basic Integration Rules

15. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
For any constant c, (c*F) ' = c*F'= c*f, so in integrals,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
∫cf dx = c∫f dx
The following is a list of integration formulas for basic
functions.
and we say that we can “integrate term by term”.
We say that we can “pull out the constant multiple.”
Basic Integration Rules

16. The procedure of finding the anti-derivatives is called
“integration”. Rewording the basic differentiation
rules, we have the following integration rules.
anti-derivatives
then (F ± G)' = F' ± G' = f + g. In integral notation,
For any constant c, (c*F) ' = c*F'= c*f, so in integrals,
Let f, g, F, G and that F' = f and G' = g,
∫f ± g dx = ∫f dx ± ∫g dx
∫cf dx = c∫f dx
The following is a list of integration formulas for basic
functions. These formulas are just the derivatives of
the basic functions written in the integral forms.
and we say that we can “integrate term by term”.
We say that we can “pull out the constant multiple.”
Basic Integration Rules

17. xpdx =
sin(x) dx = –cos(x) + k
sec(x)tan(x) dx
ex dx = ex + k
dx = ln(x) + kx
1
anti-derivatives
∫
∫
∫
∫ xP+1
P + 1 + k where P ≠ –1
cos(x) dx = sin(x) + k∫
sec2(x) dx = tan(x) + k∫ = –cot(x) + k∫
∫
= sec(x) + k
csc(x)cot(x) dx∫
= –csc(x) + k
csc2(x) dx
The Power Functions
The Trig–Functions
The Log and Exponential Functions
x–1 dx = ln(x) + k∫
or

18. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2 dx

19. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2 dx
Integrate term by term
and pull out the constant
multiple of each term.

20. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx
dx
Integrate term by term
and pull out the constant
multiple of each term.

21. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 ∫ sin(x) dx
dx
Integrate term by term
and pull out the constant
multiple of each term.

22. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
dx
Integrate term by term
and pull out the constant
multiple of each term.

23. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
dx
Integrate term by term
and pull out the constant
multiple of each term.
There is no Quotient Rule
for integration. Hence we
have to separate the
fractions.

24. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx

25. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx
Although each integral yields a
constant term, these terms may
be collected as a single “k”.

26. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx
The graphs of all the anti-derivatives
F(x) + k of f(x) are positioned by the
integration constant k.

27. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx
The graphs of all the anti-derivatives
F(x) + k of f(x) are positioned by the
integration constant k.
For example, the anti-derivatives of
2x are F(x) = x2 + k.

28. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx
The graphs of all the anti-derivatives
F(x) + k of f(x) are positioned by the
integration constant k.
For example, the anti-derivatives of
2x are F(x) = x2 + k. Their graphs
are just the vertical translations of
the parabola y = x2 “filed” by k as
shown here. Graphs of the anti-derivatives
of 2x, F(x) = x2 + k, layered by k
k=–2
k=–1
k=0
k=1
k=2

29. anti-derivatives
Example A. Find the following anti-derivative.
∫3ex – 5sin(x) + x
√x – 2
= ∫3 ex dx – 5 x–½ dx∫ dx∫ ∫ x
2sin(x) dx + –
= 3ex + 5cos(x) + 2x½ – 2 ln(x) + k
dx
The graphs of all the anti-derivatives
F(x) + k of f(x) are positioned by the
integration constant k.
For example, the anti-derivatives of
2x are F(x) = x2 + k. Their graphs
are just the vertical translations of
the parabola y = x2 “filed” by k as
shown here. All of them have
identical slope at any given x.
Graphs of the anti-derivatives
of 2x, F(x) = x2 + k, layered by k
k=–2
k=–1
k=0
k=1
k=2

30. anti-derivatives
When solving for the equation of a line with a given
derivative, i.e. its slope m, a point on the line is
needed in order to determine its equation.
anti-derivatives of 2x,
F(x) = x2 + k, “filed” by k
k=–2
k=–1
k=0
k=1
k=2
(1, 3)

31. anti-derivatives
When solving for the equation of a line with a given
derivative, i.e. its slope m, a point on the line is
needed in order to determine its equation.
Likewise if we know the derivative, i.e. the slopes,
of a function F(x) then all we need is a point to
completely determine F(x).
anti-derivatives of 2x,
F(x) = x2 + k, “filed” by k
k=–2
k=–1
k=0
k=1
k=2
(1, 3)

32. anti-derivatives
When solving for the equation of a line with a given
derivative, i.e. its slope m, a point on the line is
needed in order to determine its equation.
Likewise if we know the derivative, i.e. the slopes,
of a function F(x) then all we need is a point to
completely determine F(x).
anti-derivatives of 2x,
F(x) = x2 + k, “filed” by k
k=–2
k=–1
k=0
k=1
k=2
Such a data–point is called the
“initial condition”.
(1, 3)

33. anti-derivatives
When solving for the equation of a line with a given
derivative, i.e. its slope m, a point on the line is
needed in order to determine its equation.
Likewise if we know the derivative, i.e. the slopes,
of a function F(x) then all we need is a point to
completely determine F(x).
anti-derivatives of 2x,
F(x) = x2 + k, “filed” by k
k=–2
k=–1
k=0
k=1
k=2
Such a data–point is called the
“initial condition”. In general the
initial condition is a list of data–
points that enables us to determine
all the unspecified constants in the
general solution.
(1, 3)

34. anti-derivatives
When solving for the equation of a line with a given
derivative, i.e. its slope m, a point on the line is
needed in order to determine its equation.
Likewise if we know the derivative, i.e. the slopes,
of a function F(x) then all we need is a point to
completely determine F(x).
anti-derivatives of 2x,
F(x) = x2 + k, “filed” by k
k=–2
k=–1
k=0
k=1
k=2
Such a data–point is called the
“initial condition”. In general the
initial condition is a list of data–
points that enables us to determine
all the unspecified constants in the
general solution. So if F'(x) = 2x
with the initial condition F(1) = 3,
then it must be that F(x) = x2 + 2.
(1, 3)

35. anti-derivatives
We may recover a function completely through its
higher order derivative if we have sufficient information.

36. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) = (t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
with the initial condition

37. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) = (t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
with the initial condition

38. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) =
∫
(t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
x'(t) = (t – )2
t
1
dtSo
with the initial condition

39. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) =
∫
(t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
x'(t) = (t – )2
t
1
dt
= ∫ t2 – 2 +
t2
1 dt
So
with the initial condition

40. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) =
∫
(t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
x'(t) = (t – )2
t
1
dt
= ∫ t2 – 2 +
t2
1 dt
= t3
3
– 2t – t–1 + k
So
where k is a constant.
with the initial condition

41. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) =
∫
(t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
x'(t) = (t – )2
t
1
dt
= ∫ t2 – 2 +
t2
1 dt
= t3
3
– 2t – t–1 + k
So
We are given that x'(1) = 1/3, so = 1/31
3
– 2 – 1 + k
where k is a constant.
with the initial condition

42. anti-derivatives
Example B. Find the position function x(t) given that
x''(t) =
∫
(t – )2
t
1
x'(1) = 1/3 and that x(1) = 1/12.
We may recover a function completely through its
higher order derivative if we have sufficient information.
The 1st derivative x'(t) is the integral of the x''(t).
x'(t) = (t – )2
t
1
dt
= ∫ t2 – 2 +
t2
1 dt
= t3
3
– 2t – t–1 + k
So
We are given that x'(1) = 1/3, so = 1/31
3
– 2 – 1 + k
Therefore k = 3 and that t3
3
– 2t – t–1 + 3x'(t) =
where k is a constant.
with the initial condition

43. anti-derivatives
The function x(t) is an anti-derivative of x'(t).

44. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) = ∫ dtt3
3
– 2t – t–1 + 3

45. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K where K is a constant.

46. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
where K is a constant.

47. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
= 1/121
12
– 1 – 0 + 3 + K
where K is a constant.

48. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
= 1/121
12
– 1 – 0 + 3 + K
We have that K = –2.
where K is a constant.

49. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
= 1/121
12
– 1 – 0 + 3 + K
We have that K = –2.
Therefore x(t) = t4
12
– t2 – ln(t) + 3t – 2
where K is a constant.

50. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
= 1/121
12
– 1 – 0 + 3 + K
We have that K = –2.
Therefore x(t) = t4
12
– t2 – ln(t) + 3t – 2
where K is a constant.
As we noticed before, the formulas whose higher
order derivatives eventually become 0 are the
polynomials.

51. anti-derivatives
The function x(t) is an anti-derivative of x'(t).
So x(t) =
=
∫ dtt3
3
– 2t – t–1 + 3
t4
12
– t2 – ln(t) + 3t + K
We are given that x(1) = 1/12, so
= 1/121
12
– 1 – 0 + 3 + K
We have that K = –2.
Therefore x(t) = t4
12
– t2 – ln(t) + 3t – 2
where K is a constant.
As we noticed before, the formulas whose higher
order derivatives eventually become 0 are the
polynomials. Specifically if P(x) is a polynomial of
deg N, then P(N+1) (x) = P(N+2) (x) = P(N+3) (x) = .. = 0.

52. anti-derivatives
Theorem.
If F(N) (x) = G(N)(x) then F(x) = G(x) + P(x) for some
polynomial P(x) with deg(P) < N.

53. anti-derivatives
In other words, if two function have the same N’th
derivatives, then their difference is a polynomial with
degree less than N.
Theorem.
If F(N) (x) = G(N)(x) then F(x) = G(x) + P(x) for some
polynomial P(x) with deg(P) < N.

54. anti-derivatives
In other words, if two function have the same N’th
derivatives, then their difference is a polynomial with
degree less than N. In general, we need N data points
in the initial condition to recover the difference
P(x) completely.
Theorem.
If F(N) (x) = G(N)(x) then F(x) = G(x) + P(x) for some
polynomial P(x) with deg(P) < N.

55. The Substitution Method

56. The Substitution Method
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.

57. The Substitution Method
For example,
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.
∫sin ( )x
1
dx is not an elementary function.

58. The Substitution Method
For example,
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.
∫sin ( )x
1
dx is not an elementary function.
That is to say, there is no formula that we may build,
using the algebraic functions, the trig–functions, or
the exponential and log–functions
.

59. The Substitution Method
For example,
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.
∫sin ( )x
1
dx is not an elementary function.
That is to say, there is no formula that we may build,
using the algebraic functions, the trig–functions, or
the exponential and log–functions in finitely many
steps

60. The Substitution Method
For example,
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.
∫sin ( )x
1
dx is not an elementary function.
That is to say, there is no formula that we may build,
using the algebraic functions, the trig–functions, or
the exponential and log–functions in finitely many
steps, whose derivative is sin(1/x).

61. The Substitution Method
For example,
The derivative of an elementary function is another
elementary function, but the anti-derivative of an
elementary function might not be elementary.
∫sin ( )x
1
dx is not an elementary function.
That is to say, there is no formula that we may build,
using the algebraic functions, the trig–functions, or
the exponential and log–functions in finitely many
steps, whose derivative is sin(1/x). Because there is
no Product Rule, no Quotient Rule, and no Chain
Rule for integrations, it means that the algebra of
calculating anti-derivatives is a lot more complex than
derivatives.

62. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.

63. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
The Substitution Method reverses the Chain Rule

64. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.

65. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
The Substitution Method–Chain Rule Reversed

66. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x.

67. The Substitution Method
(f ○ u)'(x) = [f(u(x))]'
There are two main methods of integration,
the Substitution Method and Integration by Parts.
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x. By the Chain Rule,
the derivative of f with respect to x is

68. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
(f ○ u)'(x) = [f(u(x))]' = f'(u(x))u'(x),
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x. By the Chain Rule,
the derivative of f with respect to x is

69. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
(f ○ u)'(x) = [f(u(x))]' = f'(u(x))u'(x), or that
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
∫ f'(u(x))u'(x) dx f(u(x)) + k
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x. By the Chain Rule,
the derivative of f with respect to x is

70. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
(f ○ u)'(x) = [f(u(x))]' = f'(u(x))u'(x), or that
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
∫ f'(u(x))u'(x) dx
This integration rule is more useful when stated with
f’s as specific basic functions.
f(u(x)) + k
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x. By the Chain Rule,
the derivative of f with respect to x is

71. The Substitution Method
There are two main methods of integration,
the Substitution Method and Integration by Parts.
(f ○ u)'(x) = [f(u(x))]' = f'(u(x))u'(x), or that
The Substitution Method reverses the Chain Rule
and Integration by Parts unwinds the Product Rule.
∫ f'(u(x))u'(x) dx
This integration rule is more useful when stated with
f’s as specific basic functions. We list the integral
formulas from last section in their substitution–form .
f(u(x)) + k
The Substitution Method–Chain Rule Reversed
Let f = f(u) be a function of u, and u = u(x) be a
function x. By the Chain Rule,
the derivative of f with respect to x is

72. anti-derivatives
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.

73. up u'dx =
anti-derivatives
∫ uP+1
P + 1 (P ≠ –1)The Power Functions
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.
+ k

74. up u'dx =
sin(u) u'dx
anti-derivatives
∫
∫ uP+1
P + 1 (P ≠ –1)
cos(u) u'dx= sin(u) + k∫
The Power Functions
The Trig–Functions
= –cos(u) + k
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.
+ k

75. up u'dx =
sin(u) u'dx
sec(u)tan(u) u'dx
anti-derivatives
∫
∫ uP+1
P + 1 (P ≠ –1)
cos(u) u'dx= sin(u) + k∫
sec2(u) u'dx = tan(u) + k∫ = –cot(u) + k∫
∫
= sec(u) + k
csc(u)cot(u) u'dx∫
= –csc(u) + k
csc2(u) u'dx
The Power Functions
The Trig–Functions
= –cos(u) + k
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.
+ k

76. up u'dx =
sin(u) u'dx
sec(u)tan(u) u'dx
eu u'dx = eu + k
anti-derivatives
∫
∫
∫ uP+1
P + 1 (P ≠ –1)
cos(u) u'dx= sin(u) + k∫
sec2(u) u'dx = tan(u) + k∫ = –cot(u) + k∫
∫
= sec(u) + k
csc(u)cot(u) u'dx∫
= –csc(u) + k
csc2(u) u'dx
The Power Functions
The Trig–Functions
The Log and Exponential Functions
= –cos(u) + k
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.
+ k

77. up u'dx =
sin(u) u'dx
sec(u)tan(u) u'dx
eu u'dx = eu + k
dx = ln(u) + ku
u'
anti-derivatives
∫
∫
∫
∫ uP+1
P + 1 (P ≠ –1)
cos(u) u'dx= sin(u) + k∫
sec2(u) u'dx = tan(u) + k∫ = –cot(u) + k∫
∫
= sec(u) + k
csc(u)cot(u) u'dx∫
= –csc(u) + k
csc2(u) u'dx
The Power Functions
The Trig–Functions
The Log and Exponential Functions
u–1u'dx = ln(u) + k∫
or
= –cos(u) + k
In the following formulas, u = u(x) is a function of x
and u' = du/dx the derivative with respect to x.
+ k

78. The Substitution Method
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand.

79. The Substitution Method
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

80. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

81. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.
1. Identify u(x) whose
derivative u' is a factor of
the integrand.

82. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.
1. Identify u(x) whose
derivative u' is a factor of
the integrand.

83. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x)
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

84. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x) 2. Set du/dx= u' so
dx = du/ u'.
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

85. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

86. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

87. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

88. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
∫ eu cos(x)= du
cos(x)
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

89. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
∫ eu cos(x)= du
cos(x)
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

90. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
∫ eu cos(x)= du
cos(x)
∫ eu= du
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

91. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
∫ eu cos(x)= du
cos(x)
∫ eu= du = eu+ k
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

92. Example A. Find the following anti-derivative.
∫esin(x)cos(x)a. dx
The Substitution Method
1. Identify u(x) whose
derivative u' is a factor of
the integrand.Let u(x) = sin(x) where
u' = cos(x), 2. Set du/dx= u' so
dx = du/ u'.so dx = du/cos(x).
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
∫esin(x)cos(x) dx
∫ eu cos(x)= du
cos(x)
4. Write the answer in x.
∫ eu= du = eu+ k = esin(x) + k
Sub. with the u
Replace the dx
Note the presence of a “u(x)” and its derivative u' as a
factor in each integrand. Below is one way for tracking
the integrals using “substitution” after the respective
u(x) and u' are identified in the integrand.

93. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.

94. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
∫ cos(ln(x)) dx= x
1

95. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
Let u(x) = ln(x) where
u' = 1/x,
∫ cos(ln(x)) dx= x
1

96. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x
∫ cos(ln(x)) dx= x
1

97. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1

98. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
substitute with the u,
replace the dx,

99. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
substitute with the u,
replace the dx,
∫ cos(ln(x)) dx
x
1

100. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
∫ cos(u) x du
x
1
substitute with the u,
replace the dx,
∫ cos(ln(x)) dx
=
x
1

101. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
∫ cos(u) x du
x
1
∫ cos(u) du=
substitute with the u,
replace the dx,
∫ cos(ln(x)) dx
=
x
1

102. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
∫ cos(u) x du
x
1
∫ cos(u) du = sin(u) + k=
substitute with the u,
replace the dx,
∫ cos(ln(x)) dx
=
x
1

103. The Substitution Method
∫ cos(ln(x))b. dxx
1. Identify u(x) whose
derivative u' is a factor of
the integrand.
2. Set du/dx= u' so
dx = du/ u'.
3. Substitute the u into the
integrand, and replace
dx by du/u' then integrate
the new integral in u.
4. Write the answer in x.
Let u(x) = ln(x) where
u' = 1/x, or
du
dx = 1
x so xdu = dx
∫ cos(ln(x)) dx= x
1
∫ cos(u) x du
x
1
∫ cos(u) du = sin(u) + k = sin(ln(x)) + k=
substitute with the u,
replace the dx,
∫ cos(ln(x)) dx
=
x
1

104. The Substitution Method
By the Chain Rule
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
3
1

105. The Substitution Method
By the Chain Rule
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1

106. The Substitution Method
By the Chain Rule
[sin(3x + 2)]' = cos(3x + 2)(3),
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1

107. The Substitution Method
By the Chain Rule
[sin(3x + 2)]' = cos(3x + 2)(3),
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1
so [ sin(3x + 2)]' = cos(3x + 2)
3
1

108. The Substitution Method
By the Chain Rule
[sin(3x + 2)]' = cos(3x + 2)(3),
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1
so [ sin(3x + 2)]' = cos(3x + 2)
3
1
∫ cos(3x + 2) dx =Hence sin(3x + 2)
3
+ k

109. The Substitution Method
By the Chain Rule
[sin(3x + 2)]' = cos(3x + 2)(3),
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1
so [ sin(3x + 2)]' = cos(3x + 2)
3
1
∫ cos(3x + 2) dx =Hence sin(3x + 2)
3
+ k
In fact if F'(x) = f(x), then F'(ax + b) = a*f(ax + b) where
a and b are constants.

110. The Substitution Method
By the Chain Rule
[sin(3x + 2)]' = cos(3x + 2)(3),
[e3x + 2]' = e3x + 2(3), so [ (e3x + 2)]' = e3x + 2
∫ e3x + 2 dx =Hence
e3x + 2
3 + k
3
1
so [ sin(3x + 2)]' = cos(3x + 2)
3
1
∫ cos(3x + 2) dx =Hence sin(3x + 2)
3
+ k
In fact if F'(x) = f(x), then F'(ax + b) = a*f(ax + b) where
a and b are constants.
∫f(u(x)) dx = F(u(x))a + k where u(x) = ax + b.
(Linear Substitution Integrations) Let F'(x) = f(x),
1then

111. The Substitution Method
Therefore
∫ e – ½ x + 5 dx =
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
=
∫ dx =
1
i.
ii.
iii.
√–5x + 3)
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

112. The Substitution Method
Therefore
∫ e – ½ x + 5 dx = –2e – ½ x + 5
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
+ k
∫ dx =
1
i.
ii.
iii.
√–5x + 3)
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

113. The Substitution Method
Therefore
∫ e – ½ x + 5 dx = –2e – ½ x + 5
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
= –csc( x + 2)*√2
π √2
π
+ k
+ k
∫ dx =
1
i.
ii.
iii.
√–5x + 3)
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

114. The Substitution Method
Therefore
∫ e – ½ x + 5 dx = –2e – ½ x + 5
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
= –csc( x + 2)*√2
π √2
π
+ k
+ k
∫ dx =
1
i.
ii.
iii. ∫(–5x + 3) –½ dx
√–5x + 3)
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

115. The Substitution Method
Therefore
∫ e – ½ x + 5 dx = –2e – ½ x + 5
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
= –csc( x + 2)*√2
π √2
π
+ k
+ k
∫ dx =
–5
1
i.
ii.
iii. ∫(–5x + 3) –½ dx
√–5x + 3)
= 2 * (–5x + 3) ½ *
1 + k
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

116. The Substitution Method
Therefore
∫ e – ½ x + 5 dx = –2e – ½ x + 5
∫ csc( x + 2) cot( x + 2) dx√2
π
√2
π
= –csc( x + 2)*√2
π √2
π
+ k
+ k
∫ dx =
1
i.
ii.
iii. ∫(–5x + 3) –½ dx
√–5x + 3)
–5
= + k2(–5x + 3) ½
–5= 2 * (–5x + 3) ½ *
1 + k
1. First guess the obvious
incorrect answer.
2. Take its derivative
which would be off by
a constant multiple due
to the chain rule.
3. Adjust the incorrect
answer to compensate
for the constant multiple.

117. anti-derivatives
Following is a proof based on the Mean Value
Theorem that gives us the converse of the fact that
“the derivative of a constant function f(x) = k is 0”.
Proof.
Theorem.
If f'(x) = 0 for all x’s then f(x) = k is a constant function.
We will show that for any x > 0 that f(x) = f(0) = k.
We are given that f'(x) = 0 so f(x) is differentiable.
By the Mean Value Theorem, there is a “c” where
0 < c < x and that
f(x) – f(0)
x – 0
= f '(c) = 0 by the assumption,
hence f(x) – f(0) = 0, or that f(x) = f(0) = k. A similar
argument may be made for x < 0, hence f(x) = k.