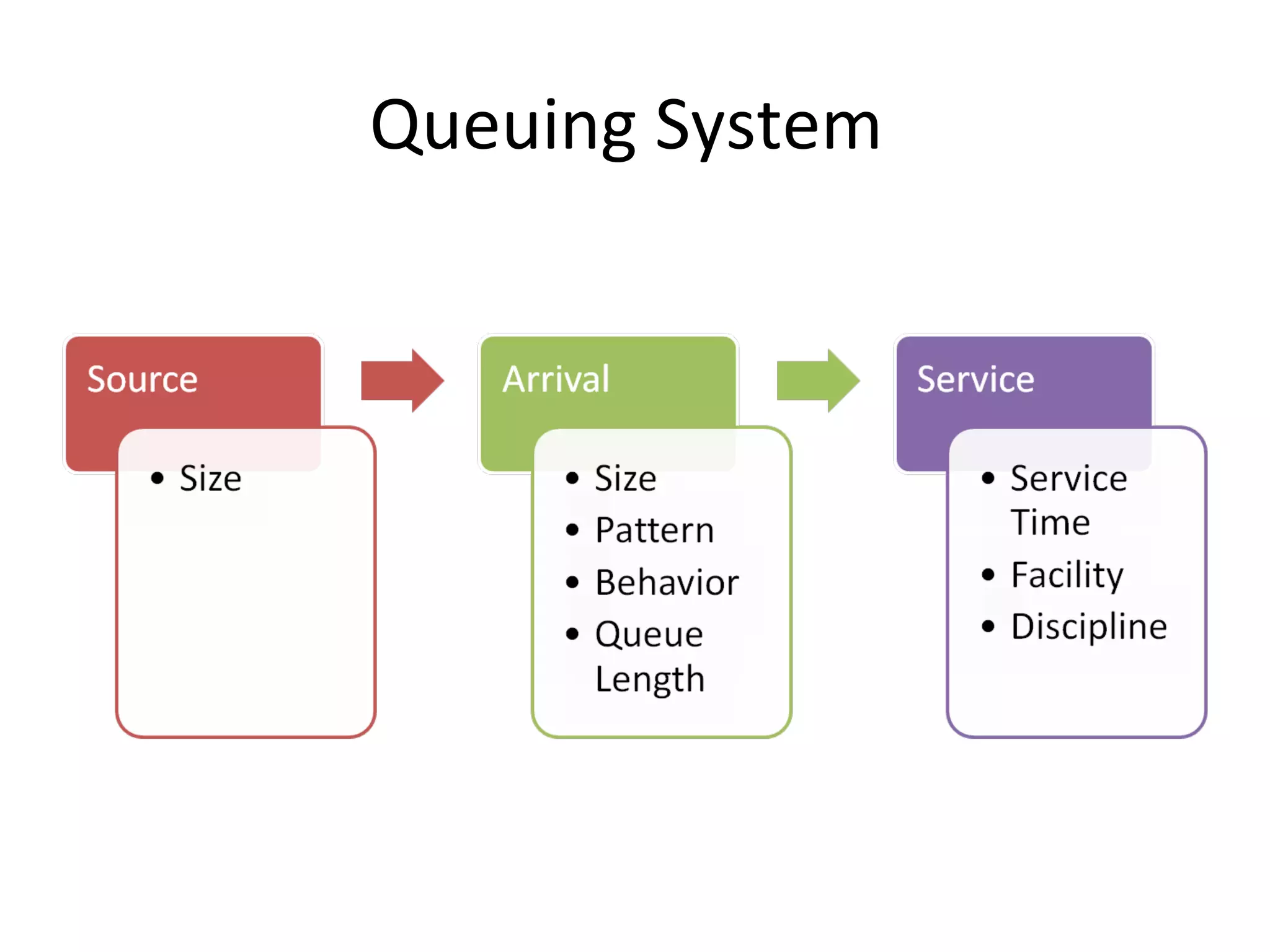
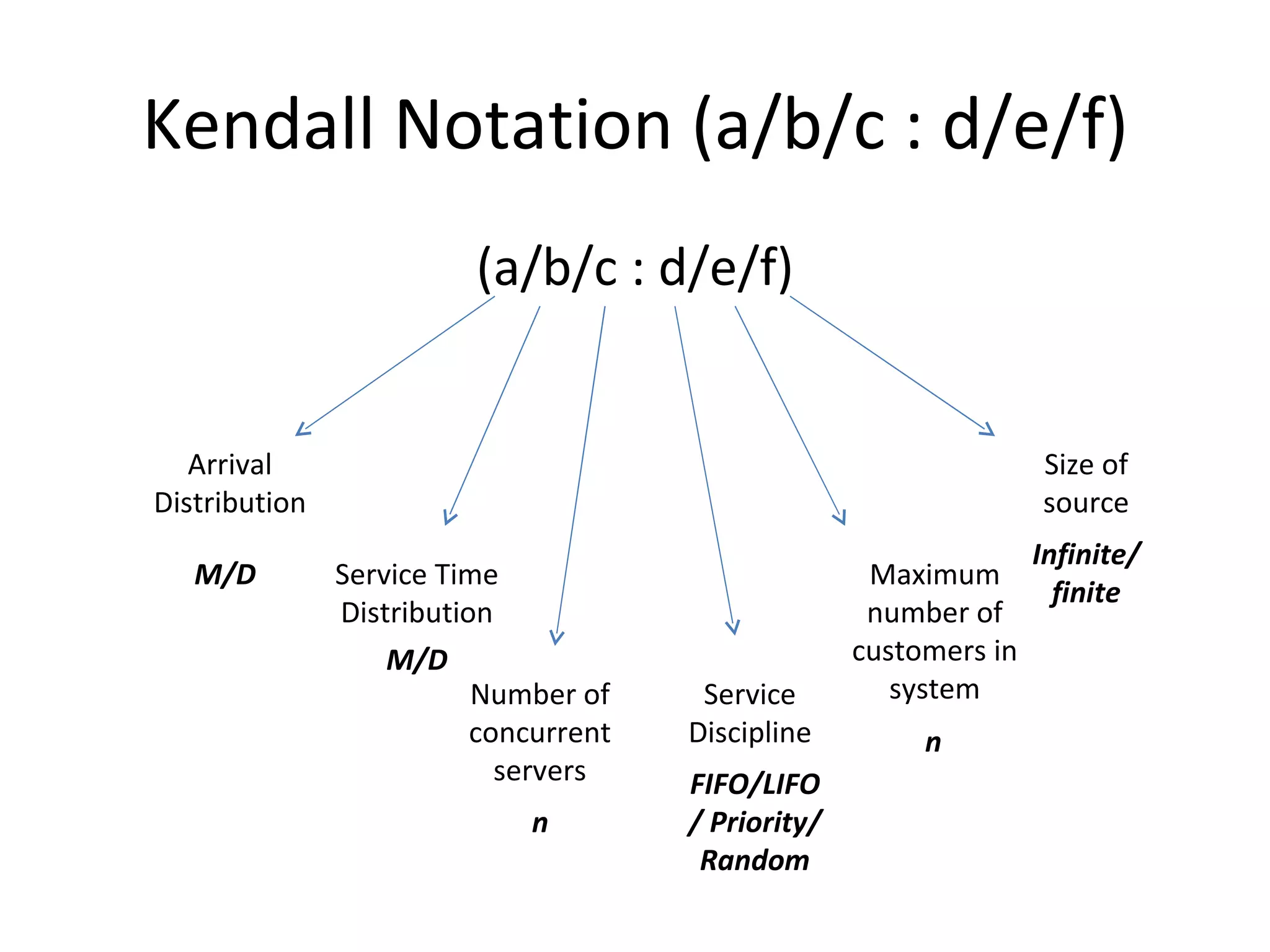
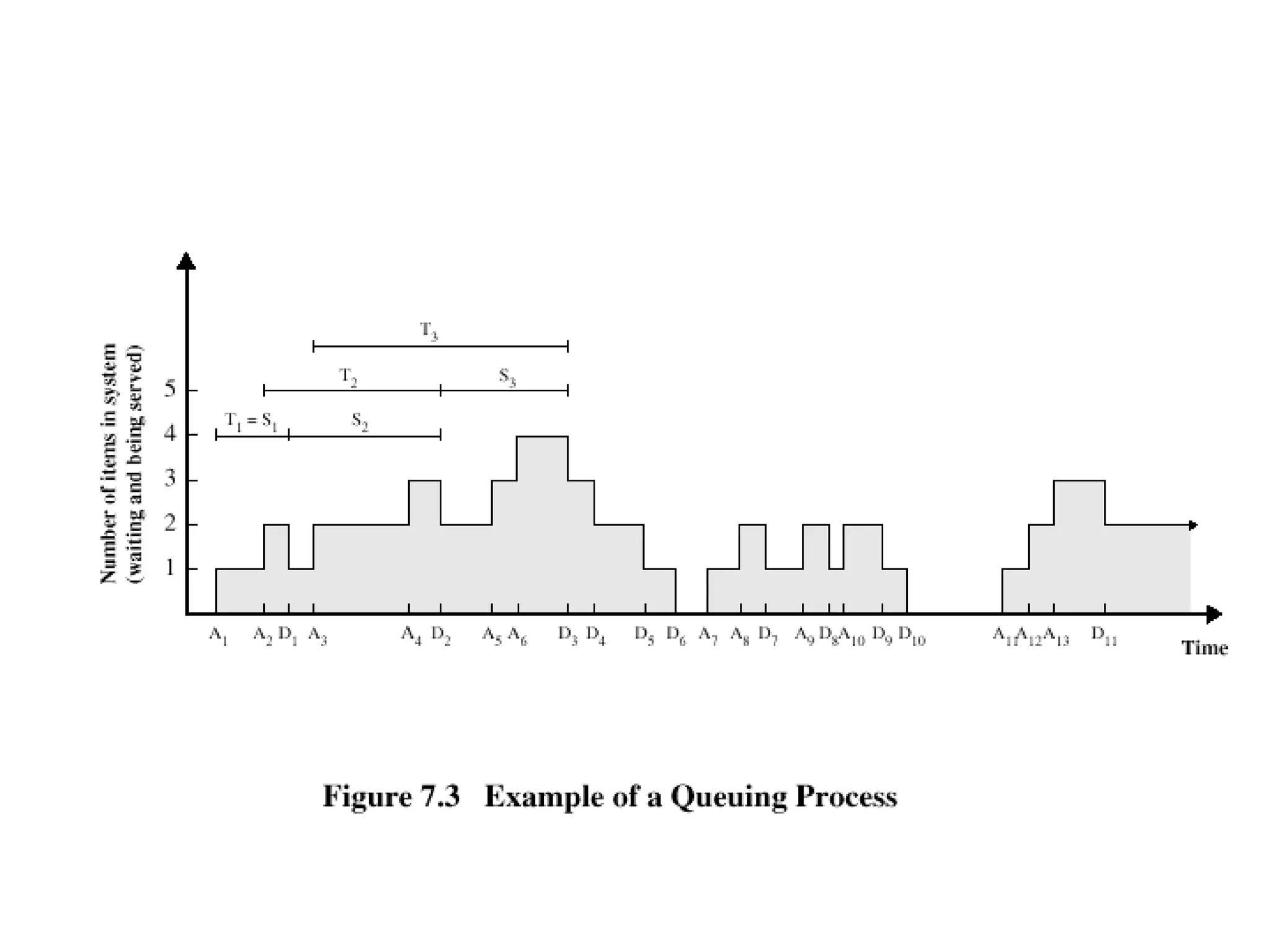
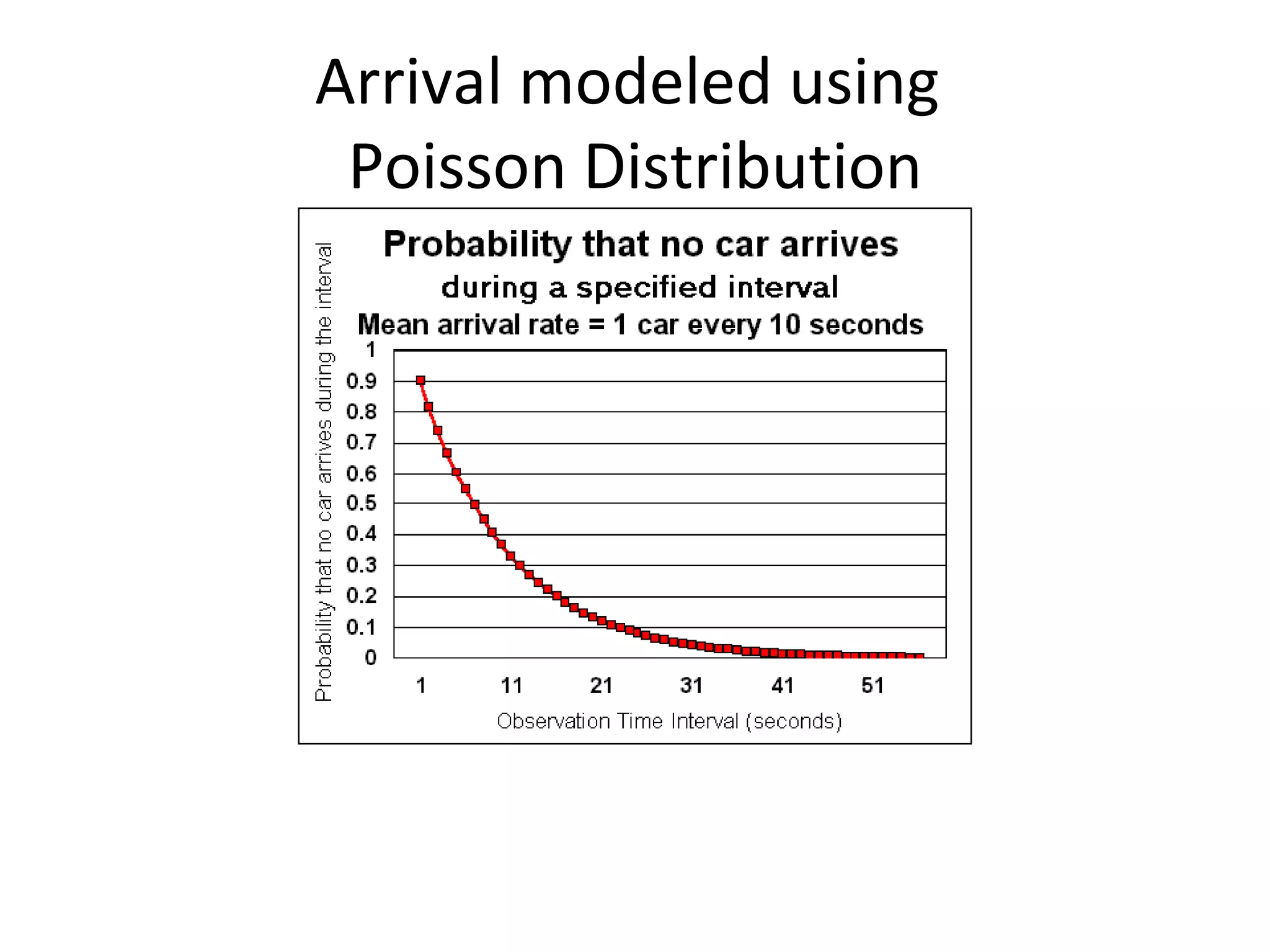
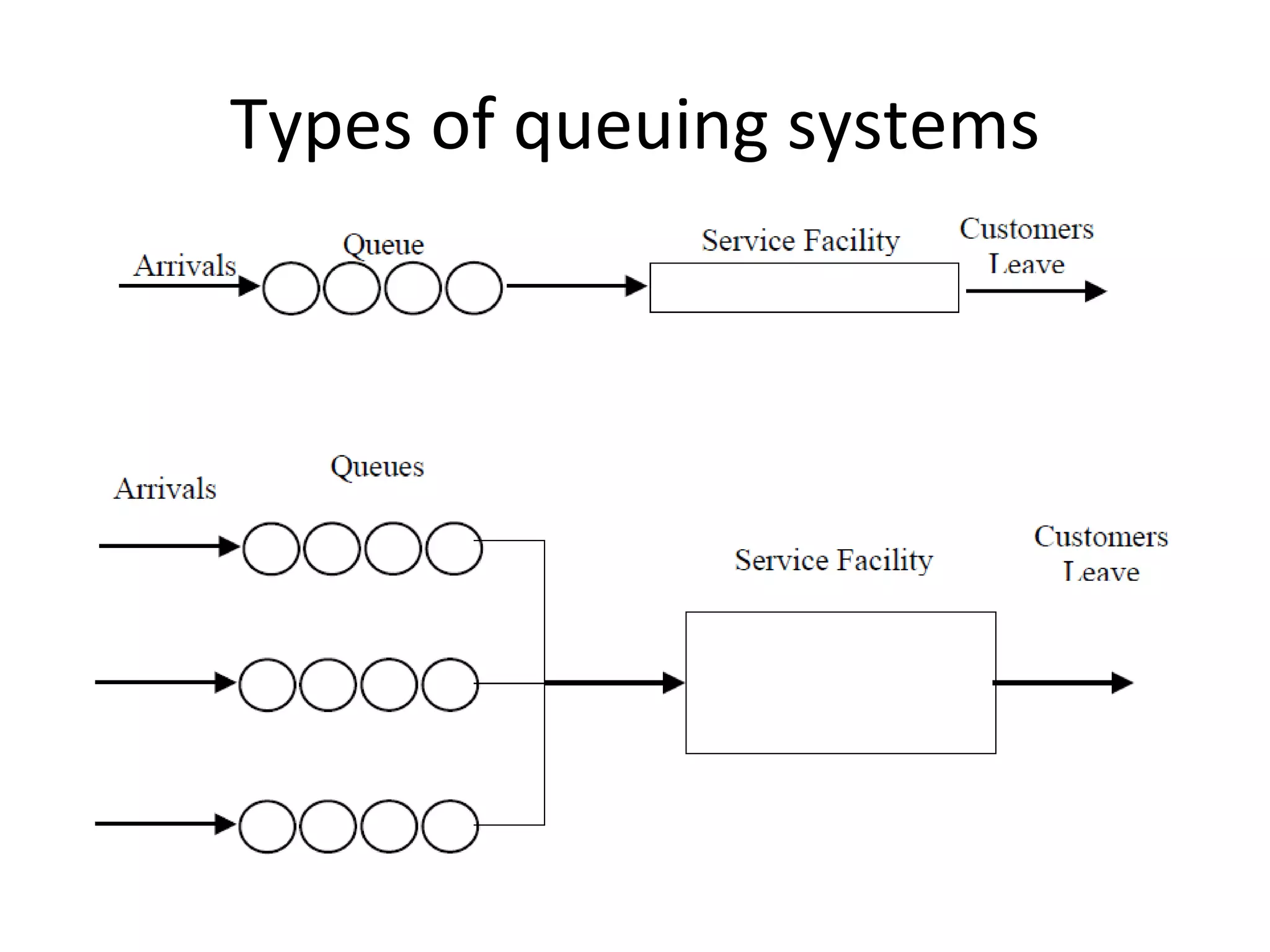
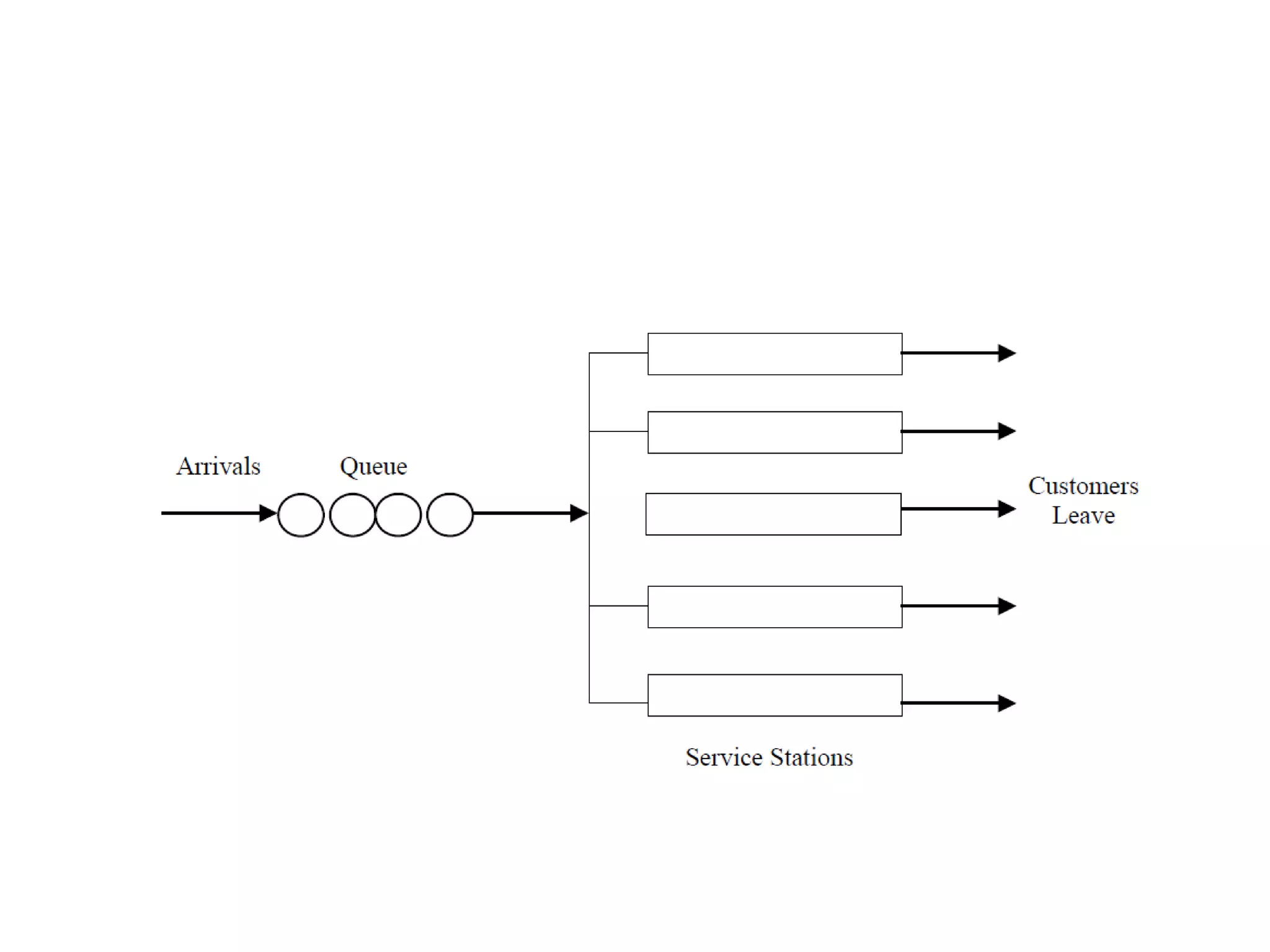
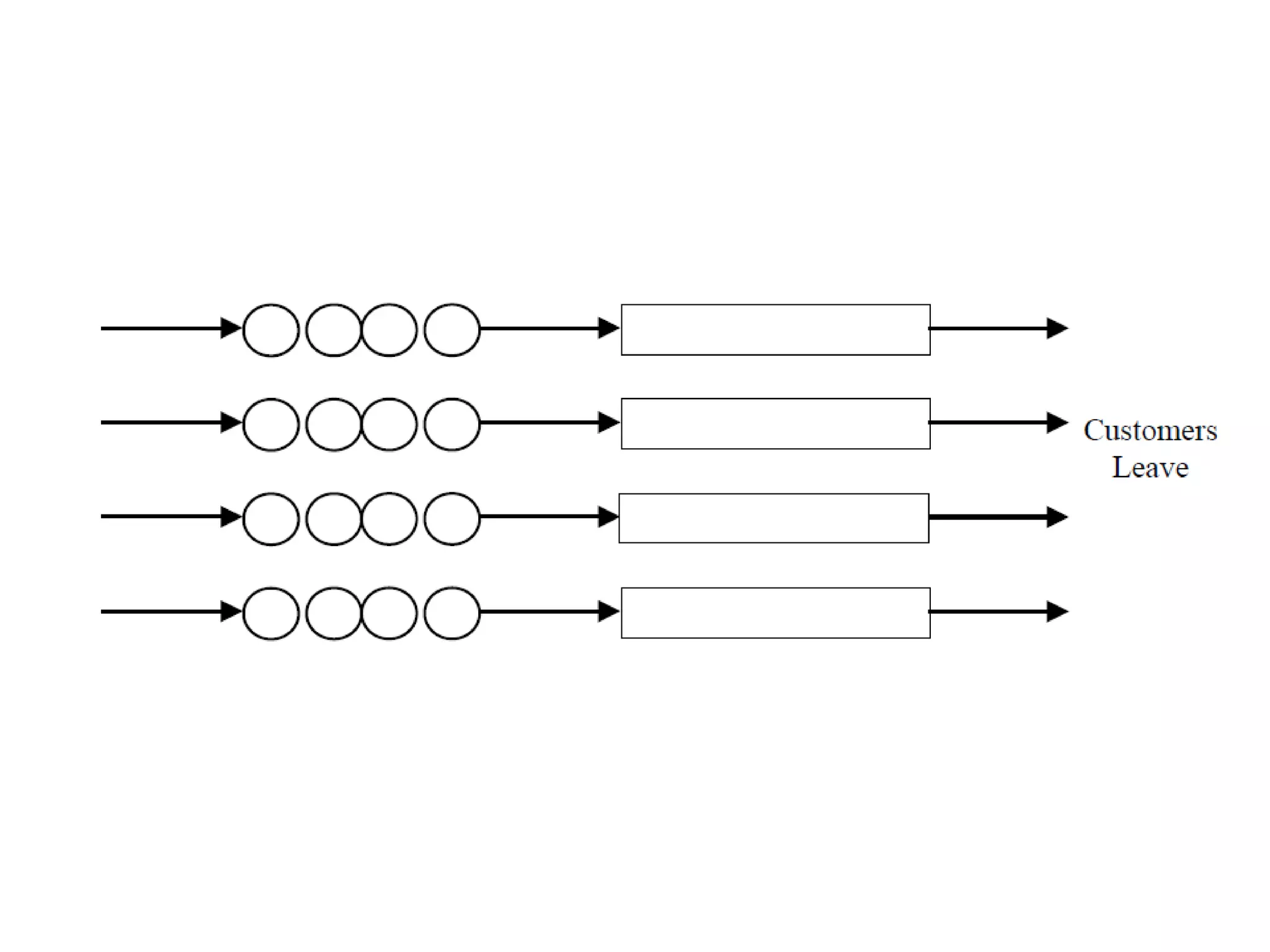
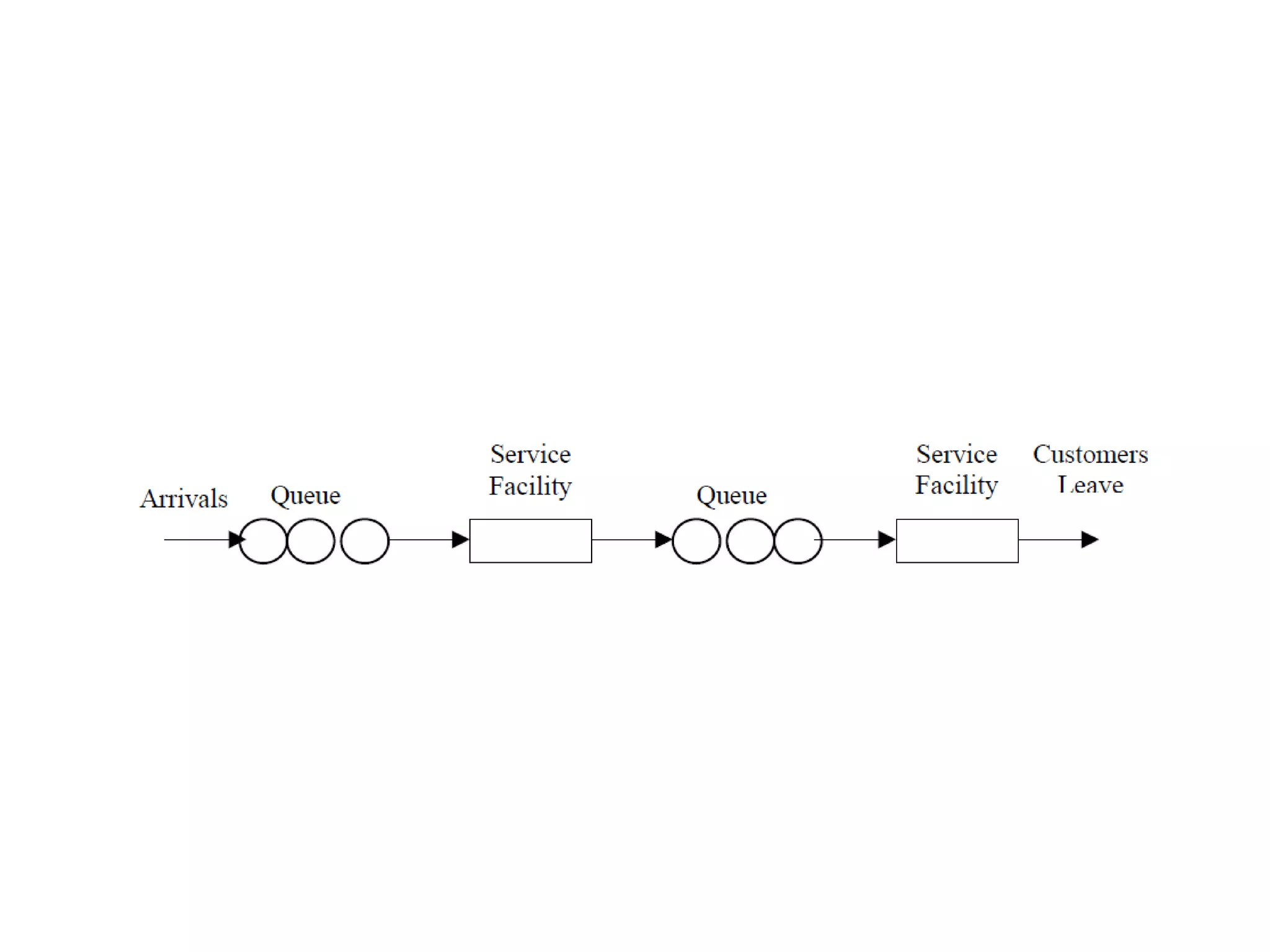
Queuing theory is the study of congestion and waiting in line systems. It examines queues that form when demand for a service exceeds the available resources, such as people waiting at a supermarket checkout, letters waiting to be processed at a post office, or cars waiting at a traffic signal. Queuing systems can be modeled and analyzed using notations like Kendall's notation to understand characteristics like expected wait times, number of servers needed, and how to manage peak traffic periods. The origins of queuing theory began with the research of A.K. Erlang in the early 1900s on modeling telephone traffic and wait times.

1. Queuing Theory –
Study of Congestion
Operations Research

2. What is a queue?
• People waiting for service
– Customers at a supermarket (IVR, railway counter)
– Letters in a post office (Emails, SMS)
– Cars at a traffic signal
• In ordered fashion (who defines order?)
– Bank provides token numbers
– Customers themselves ensure FIFO at Railway
ticket counters

3. Where do we find queues?

4. A thought experiment
• When does a queue form?
• When will it not form?
• When will you not join a queue?
• When will you leave a queue?
• What is the worst case scenario?

5. What do you observe near a queue?
• Conflict
• Congestion
• Idle counters
• Overworked counters
• Smart people trying to circumvent the queue

6. What do we want to know?
• How much time will it take?
• How many counters should be there?
• How to manage peak hour traffic?

7. Origins
• Queuing Theory had its beginning in the research
work of a Danish engineer named A. K. Erlang.
• In 1909 Erlang experimented with fluctuating
demand in telephone traffic.
• Eight years later he published a report addressing
the delays in automatic dialing equipment.
• At the end of World War II, Erlang’s early work
was extended to more general problems and to
business applications of waiting lines.

8. Queuing System

9. Kendall Notation (a/b/c : d/e/f)
(a/b/c : d/e/f)
Arrival Size of
Distribution source
Infinite/
M/D Service Time Maximum
finite
Distribution number of
M/D customers in
Number of Service system
concurrent Discipline n
servers FIFO/LIFO
n / Priority/
Random

10. Identify the queuing system
Railway ticket counter (M/D/3:FIFO/200/∞)
Bank Service Counter
ATM
Airport – Check In
Airport - Security
Traffic Signal
Bus Stop
Train Platform (Boarding)
Paper Correction

12. Arrival modeled using
Poisson Distribution

13. Some parameters
Arrival Rate λ
Service Rate μ
Number of customers in system Ls
Number of customers in queue Lq
Waiting time in system Ws
Waiting time in queue Wq
Utilization ρ

14. Types of queuing systems

19. M/M/1

20. T1=3
T2=7 Arrival Rate = N/Tt=6/19=.31
T3=10 Mean Time in system = J/N = 38/6=6.3
T4=6 Mean number in system = J/Tt=38/19=2
T5=6 = (J/N)*(N/Tt)=6.3*.31=2
T6=6 =λTq
J=38