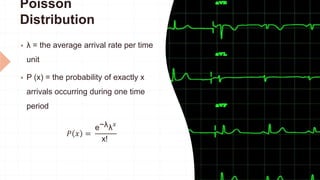
Queuing theory is the mathematical study of waiting lines in systems like customer service lines. Key aspects of queuing systems include the arrival and service processes, the number of servers, and the queue capacity and discipline. Little's Law relates the average number of customers in the system, the arrival rate, and the average time a customer spends in the system. Common queuing models include M/M/1 for Poisson arrivals and exponential service times with one server.

1. Queing Theory
Dr Renjith V. Ravi Ph. D, FIETE, C. Eng. (IE)
Associate Professor and Head,
Department of Electronics and Communication Engineering
M.E.A Engineering College,
Malappuram District, Kerala, India 679 325
ORCID: 0000-0001-9047-3220

2. Learning
Outcomes
To develop the modeling and
mathematical skills to analytically
determine computer systems and
analytically determine computer systems
and communication network performance
Students should be able to read and
understand the current performance
analysis and queueing theory literature
upon completion of the course
Understand strengths and weaknesses of
Queueing Models

3. Introductio
n to
Queuing
Theory
Queuing theory (or queueing theory) refers to the
mathematical study of the formation, function,
and congestion of waiting lines, or queues
At its core, a queuing situation involves two parts
Someone or something that requests a
service—usually referred to as the
customer, job, or request
Someone or something that completes or
delivers the services—usually referred to
as the server

4. To illustrate, let’s take two examples
 When looking at the queuing situation at a bank, the customers are people
seeking to deposit or withdraw money, and the servers are the bank tellers
 When looking at the queuing situation of a printer, the customers are the
requests that have been sent to the printer, and the server is the printer
 Queuing theory scrutinizes the entire system of waiting in line, including
elements like the customer arrival rate, number of servers, number of
customers, capacity of the waiting area, average service completion time,
and queuing discipline
 Queuing discipline refers to the rules of the queue, for example whether it
behaves based on a principle of first-in-first-out, last-in-first-out, prioritized,
or serve-in-random-order
Population of Customers
Out
put
Se
rve
r
Que
ue
Arr
iva
l

5. How did queuing theory start?
 Queuing theory was first introduced in the early
20th century by Danish mathematician and
engineer Agner Krarup Erlang
 Erlang worked for the Copenhagen Telephone
Exchange and wanted to analyze and optimize its
operations
 He sought to determine how many circuits were
needed to provide an acceptable level of telephone
service, for people not to be “on hold” for too long
 His mathematical analysis culminated in his 1920
paper “Telephone Waiting Times”, which served as the
foundation of applied queuing theory
 The international unit of telephone traffic is called the
Erlang in his honor
Source: Telephone operators at work

6. Kendall's
Notation
 In queueing theory, a discipline within the
mathematical theory of probability, Kendall's notation (or
sometimes Kendall notation) is the standard system used to
describe and classify a queueing node.
 D. G. Kendall proposed describing queueing models using
three factors written A/S/c in 1953 where A denotes the time
between arrivals to the queue, S the service time distribution
and c the number of service channels open at the node.
 It has since been extended to A/S/c/K/N/D where K is the
capacity of the queue, N is the size of the population of jobs
to be served, and D is the queueing discipline, assumed first-
in-first-out if omitted.
 When the final three parameters are not specified (e.g. M/M/1
queue), it is assumed K = ∞, N = ∞ and D = FIFO.

7. Queueing
Discipline
 A network scheduler, also called packet
scheduler, queueing discipline (qdisc) or
queueing algorithm, is an arbiter on a node in a
packet switching communication network.
 It manages the sequence of network packets in
the transmit and receive queues of the protocol
stack and network interface controller.
 There are several network schedulers available
for the different operating systems, that
implement many of the existing network
scheduling algorithms.

8. Queuing
Disciplines
First-in, first-out queuing
Last-in, first-out queuing
Priority queuing

9. What are the different types of queuing
systems?
 For example, think of an ATM
 It can serve: one customer at a time; in a first-in-first-out
order; with a randomly-distributed arrival process and
service distribution time; unlimited queue capacity; and
unlimited number of possible customers
 Queuing theory would describe this system as a M/M/1
queue
 Queuing theory calculators out there often require
choosing a queuing system from the Kendall notation
before calculating inputs
Que in front of an ATM

10. Packet Switching:
queueing delay, loss
 Queuing and loss
 § packets will queue, wait to be
transmitted on link
 § packets can be dropped if memory fills
up

11. Why is queuing theory
important?
 Waiting in line is a part of everyday life
because as a process it has several important
functions
 Negative outcomes arise if a queue process
isn’t established to deal with overcapacity
 For example, when too many visitors navigate
to a website, the website will slow and crash if
it doesn’t have a way to change the speed at
which it processes requests or a way to queue
visitors

12. What are the
applications of
queuing theory?
 Queuing theory is powerful because the ubiquity of queue
situations means there are countless and diverse
applications of queuing theory
 Queuing theory has been applied, just to name a few, to
 Telecommunications, transportation, logistics, finance,
emergency services
 Computing, industrial engineering, project management
 Before we look at some specific applications, it’s helpful to
understand Little’s Law, a formula that helps to
operationalize queuing theory in many of these
applications

13. Little’s Law
 Little’s Law connects the capacity of a queuing
system, the average time spent in the system, and
the average arrival rate into the system without
knowing any other features of the queue
 The formula is quite simple and is written as
follows 𝐿 = 𝜆𝑊
 or transformed to solve for the other two variables
so that
𝜆 =
𝐿
𝑊
𝑊 =
𝐿
𝜆
 Where: L is the average number of customers in
the system, λ is the average arrival rate into the
system, W is the average amount of time spent in
the system

14. Little’s Law Applied to
Real-World Situations
 Little’s Law gives powerful insights because it lets us solve for
important variables like the average wait of in a queue or the number
of customers in queue simply based on two other inputs
 A line at a cafe
 For example, if you’re waiting in line at a Starbucks, Little’s Law
can estimate how long it would take to get your coffee
 Assume there are 15 people in line, one server, and 2 people are
served per minute
 To estimate this, you’d use Little’s Law in the form:
𝜆 =
𝐿
𝑊
 Showing that you could expect to wait 7.5 minutes for your coffee
15 𝑝𝑒𝑜𝑝𝑙𝑒 𝑖𝑛 𝑙𝑖𝑛𝑒
2 𝑝𝑒𝑜𝑝𝑙𝑒 𝑠𝑒𝑟𝑣𝑒𝑑 𝑝𝑒𝑟 𝑚𝑖𝑛𝑢𝑡𝑒
= 7.5 𝑀𝑖𝑛𝑢𝑡𝑒𝑠 𝑜𝑓 𝑊𝑎𝑖𝑡𝑖𝑛𝑔

15. Little's Law in Star Bucks

16. Characteristics of a
Queuing System
 The queuing system is determined by
 Arrival characteristics
 Queue characteristics
 Service facility characteristics

17. Arrival
Characteristics
 Size of the arrival population – either
infinite or limited
 Arrival distribution
 Either fixed or random
 Either measured by time between consecutive
arrivals, or arrival rate
 The Poisson distribution is often used for
random arrivals

18. Poisson
Distribution
 Average arrival rate is known
 Average arrival rate is constant for
some number of time periods
 Number of arrivals in each time
period is independent
 As the time interval approaches 0,
the average number of arrivals
approaches 0

19. Poisson
Distribution
 λ = the average arrival rate per time
unit
 P (x) = the probability of exactly x
arrivals occurring during one time
period
𝑃 𝑥 =
e−λλ𝑥
x!

20. Behaviour of Arrivals
 Most queuing formulas assume that
all arrivals stay until service is
completed
 Balking refers to customers who do
not join the queue
 Reneging refers to customers who
join the queue but give up and leave
before completing service

21. Queue Characteristics
 Queue length
 either limited or unlimited
 Service discipline
 usually FIFO
 Last-in, first-out queuing
 Priority queuing

22. Service Facility
Characteristics
 Configuration of service facility
 Number of servers
 Number of phases
 Service distribution
 The time it takes to serve 1 arrival
 Can be fixed or random
 Exponential distribution is often used

23. Exponential
Distribution
 μ = average service time
 t = the length of service time (t > 0)
 P(t) = probability that service time
will be greater than t
𝑃(𝑡) = 𝑒−𝜇𝑡

24. Kendall’s Notation
 A = Arrival distribution
 (M for Poisson, D for deterministic, and G for
general)
 B = Service time distribution
 (M for exponential, D for deterministic, and G for
general)
 S = number of servers

25. Examples for Kendall’s
Notation
Name Models
Covered (Kendall
Notation)
Example
Simple system
(M / M / 1)
Customer service desk in
a store
Multiple server
(M / M / s)
Airline ticket counter
Constant service
(M / D / 1)
Automated car wash
General service (M /
G / 1)
Auto repair shop
Limited population
(M / M / s / ∞ / N)
An operation with only 12
machines that might
break

26. M/G/1 Queueing
System
A single queue with a single
server
Customers arrive according to a
Poisson process with rate λ
The mean and second moment
of the service time are 1/µ and
X2

27. M/G/1 Queue
 In queueing theory, a discipline within the
mathematical theory of probability
 An M/G/1 queue is a queue model where arrivals
are
 Markovian (modulated by a Poisson process),
 Service times have a General distribution and
 There is only 1 single server
 The model name is written in Kendall's notation,
and is an extension of the M/M/1 queue, where
service times must be exponentially distributed
 The classic application of the M/G/1 queue is to
model performance of a fixed head hard disk

28. Model Definition
 A queue represented by a M/G/1 queue is a stochastic
process whose state space is the set {0,1,2,3...}, where
the value corresponds to the number of customers in
the queue, including any being served.
 Transitions from state i to i + 1 represent the arrival of a
new customer: the times between such arrivals have
an exponential distribution with parameter λ.
 Transitions from state i to i − 1 represent a customer
who has been served, finishing being served and
departing: the length of time required for serving an
individual customer has a general distribution function.
 The lengths of times between arrivals and of service
periods are random variables which are assumed to
be statistically independent.

29. Scheduling
Policies
Customers are typically served on a first-come, first-
served basis, other popular scheduling policies include
• Processor sharing where all jobs in the queue share the
service capacity between them equally
• Last-come, first served without preemption where a job in
service cannot be interrupted
• Last-come, first served with preemption where a job in
service is interrupted by later arrivals, but work is conserved
• Generalized foreground-background (FB) scheduling also
known as least-attained-service where the jobs which have
received least processing time so far are served first and
jobs which have received equal service time share service
capacity using processor sharing

30. Scheduling
Policies
• Shortest job first without preemption (SJF)
where the job with the smallest size receives
service and cannot be interrupted until service
completes
• Preemptive shortest job first where at any
moment in time the job with the smallest
original size is served
• Shortest remaining processing time (SRPT)
where the next job to serve is that with the
smallest remaining processing requirement

31. References
1. Q. I. (2024, February 9). Queuing theory: Definition, history
& real-life applications & examples. URL
2. Boucherie, R. J., & van Dijk, N. M. (2010). Queueing networks:
A fundamental approach. Springer.
3. Robertazzi, T. G. (2000). Computer networks and systems:
Queueing theory and performance evaluation. Springer Science
& Business Media.
4. Dattatreya, G. R. (2008). Performance analysis of queuing and
computer networks. CRC Press.
5. Ng, P. C.-H., & Boon-Hee, P. S. (2008). Queueing modelling
fundamentals: With applications in communication networks.
John Wiley & Sons.
6. Alfa, A. S. (2010). Queueing theory for telecommunications:
Discrete time modelling of a single node system. Springer
Science & Business Media.
7. Giambene, G. (2021). Queuing theory and telecommunications:
Networks and applications. Springer Nature.
8. Bose, S. K. (2013). An introduction to queueing systems.
Springer Science & Business Media.

32. Important Topics
for Examination
 Characteristics of Queueing Systems
 Kendall’s Notation
 Littles Theorem
 M/G/1 Queuing Model
 Poisson process

33. Assessment
Questions
1. What is meant by queue Discipline ?
2. Define Little’s formula
3. If people arrive to purchase cinema tickets at the average rate
of 6 per minute, it takes an average of 7.5 seconds to purchase
a ticket
4. If λ, µ are the rates of arrival and departure in a M/M/I queue
respectively, give the formula for the probability that there are n
customers in the queue at any time in steady state
5. If λ, µ are the rates of arrival and departure respectively in a
M/M/I queue, write the formulas for the average waiting time of
a customer in the queue and the average number of customers
in the queue in the steady state.
6. If the arrival and departure rates in a public telephone booth
with a single phone are 1/12 and1 /14 respectively, find the
probability that the phone is busy