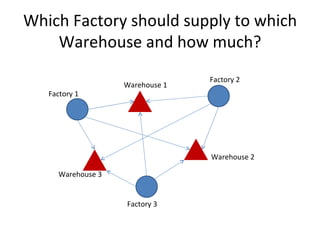
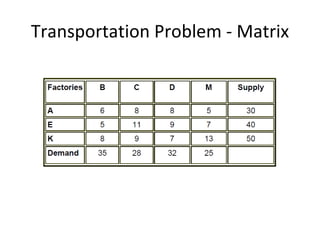
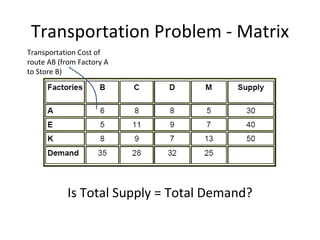
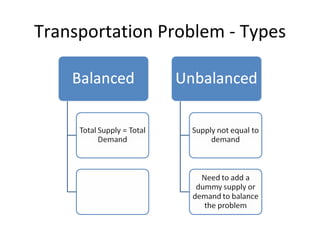
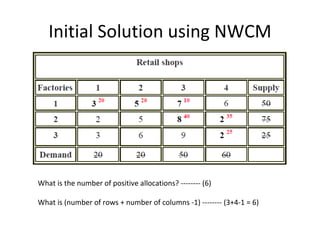
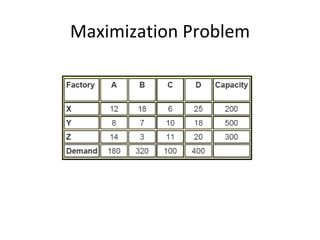
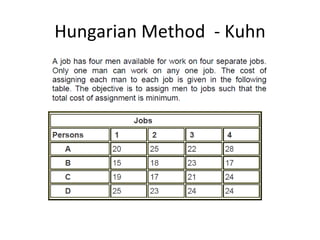
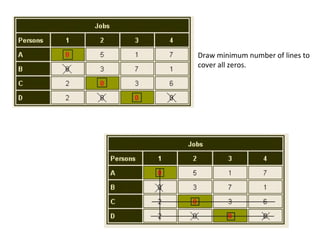
This document discusses transportation problems and their solutions. It describes transportation problems as involving determining which factories should supply which warehouses and in what amounts. It presents transportation problems as linear programming problems that can be formulated into a matrix. It then describes various methods for finding initial basic feasible solutions such as the North West Corner Method and Minimum Cost Method. It also discusses testing solutions for optimality and special cases like unbalanced problems, degeneracy, and maximization problems.

1. Transportation and Assignment
Problems
Operations Research

2. Which Factory should supply to which
Warehouse and how much?
Factory 2
Warehouse 1
Factory 1
Warehouse 2
Warehouse 3
Factory 3

3. What is a transportation problem?

4. Transportation as a Linear
Programming Problem

5. Transportation Problem - Matrix

6. Transportation Problem - Matrix
Transportation Cost of
route AB (from Factory A
to Store B)
Is Total Supply = Total Demand?

7. Transportation Problem - Types

8. How to solve a transportation
problem?
1. Formulate the problem and set up in matrix
form
2. Obtain initial basic feasible solution
3. Test the solution for optimality
4. If yes, Stop
5. If no, determine new optimal solution
6. Go to step 3

9. Methods for finding initial solution
• North West Corner Method
• Minimum Matrix Method
• Vogel’s Corner Method

10. North West Corner Method

11. Initial Solution using NWCM
What is the number of positive allocations? -------- (6)
What is (number of rows + number of columns -1) -------- (3+4-1 = 6)

12. Testing for optimality
• Is there any alternative route (empty cell)
which is better than existing routes?
• i.e. If I shift one unit from current route to any
other route, does overall cost increase or
decrease?
• Which out of alternative routes is best (which
one reduces cost by maximum amount)?

13. Stepping Stones Method
To evaluate each empty cell, draw a closed path starting at empty cell
and returning to empty cell through at least 3 occupied cells.
Add +1 (one unit) to the empty cell.
Correspondingly subtract/ add one unit to each occupied cell on the
closed path so that row and column sums remain balanced.
Increase in transportation cost = +4-6+5-3 = 0.
There is no benefit to be gained by shifting units
to route AD.

14. Initial solution itself
was optimal in this case!

15. Special Cases
• Multiple optimum solution – A scenario where
multiple routes have same overall cost.
• Unbalanced transportation problem - If total
supply not equal to total demand
• Degeneracy – number of positive allocations <
(number of rows + number of columns -1)
• Maximization

16. Unbalanced transportation problem
– If supply is more add a dummy demand column
– If demand is more add a dummy supply column
– Dummy cells have transportation cost zero
Which one is greater,
demand or supply?
What should we add, dummy
row or column?

17. Now solve using regular approach

18. Degeneracy

19. Degeneracy - Setting up a new
problem
• Introduce artificial small quantity d that doesn’t
otherwise impact supply-demand constraints

21. Maximization Problem

22. Convert to minimization problem

23. Assignment Problem
• Special case of transportation problem
• Here each source can supply to only one
destination
– Number of sources equal to number of destinations
– Only one unit supplied from source to destination
• Assigning jobs to workers
• Assigning teachers to classes
• Can be solved using simple enumeration of
combinations, regular transportation method or
simplex method

24. Hungarian Method - Kuhn

26. Identify rows with exactly one zero.
Draw a square on that zero. Cross out
all other zeros in that column.
If all zeros have either been marked
Identify columns with exactly one with square or crossed out –
zero. Draw a square on that zero.
Cross out all other zeros in that row. If there is at least one and only one
square in each row, problem has been
solved.

27. Draw minimum number of lines to
cover all zeros.

30. Special cases
• Unbalanced – Sources and Destinations not
equal.
– Add a dummy source or destination with 0 cost.
• Maximization
– Convert to minimization problem using
opportunity cost