Downloaded 152 times
Uploaded byHossam Shafiq I
Traffic Concepts (Transportation Engineering)
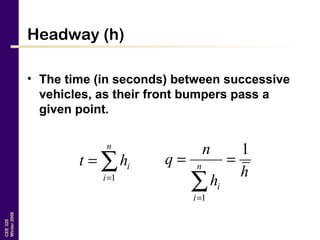
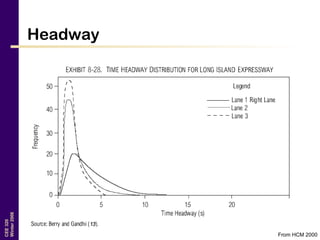
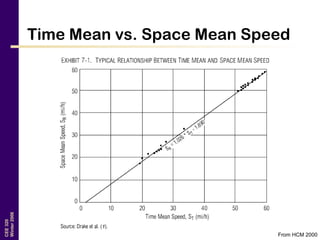
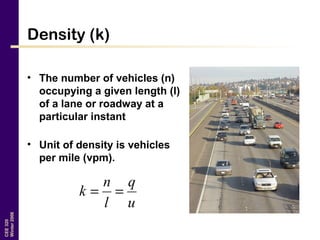
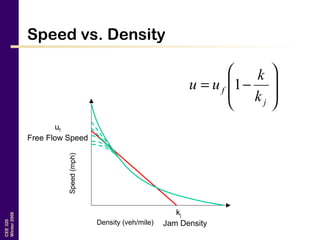
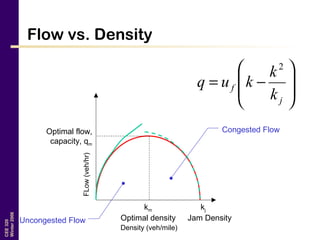
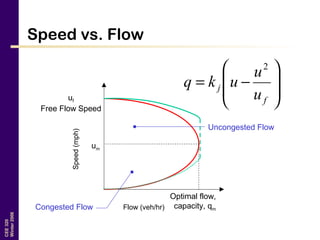
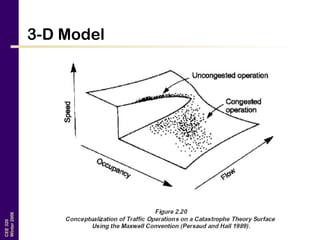
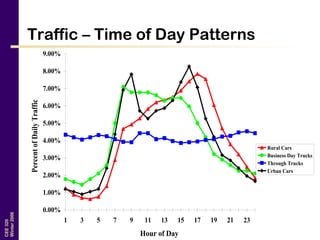
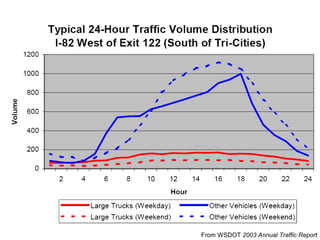
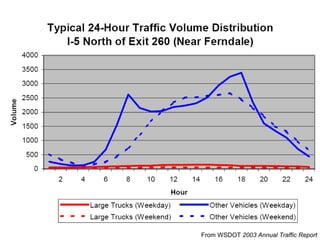
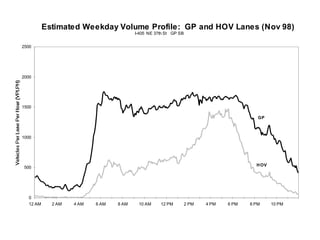
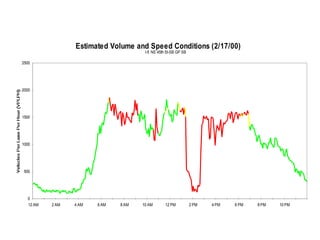
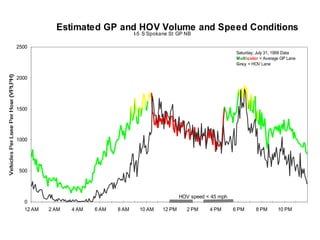
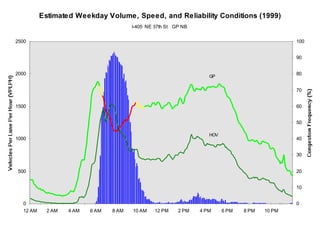
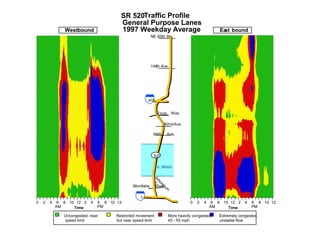
This document discusses key traffic concepts such as flow rate, spacing, headway, speed, and density. It defines these terms and explores the relationships between volume, speed, and density. Flow rate, spacing, headway, time mean speed and space mean speed are defined. Speed-density and flow-density relationships are presented, showing how traffic flow transitions from uncongested to congested states. Examples of traffic patterns by time of day and location are shown.
More Related Content
Similar to Traffic Concepts (Transportation Engineering)
![11 Geometric Design of Railway Track [Vertical Alignment] (Railway Engineerin...](https://cdn.slidesharecdn.com/ss_thumbnails/geometricdesignofrailwaytrack-ii-200415172410-thumbnail.jpg?width=640&height=640&fit=bounds)
![10 Geometric Design of Railway Track [Horizontal Alignment] (Railway Engineer...](https://cdn.slidesharecdn.com/ss_thumbnails/geometricdesignofrailwaytrack-i-200415171932-thumbnail.jpg?width=640&height=640&fit=bounds)
![[Deck] What's New in Spark-Iceberg Integration via DSV2.pptx](https://cdn.slidesharecdn.com/ss_thumbnails/deckwhatsnewinspark-icebergintegrationviadsv2-260210005337-25955b12-thumbnail.jpg?width=640&height=640&fit=bounds)
Traffic Concepts (Transportation Engineering)
- 1.
- 2. CEE320 Winter2006 Outline 1. Basic Concepts a.Flow Rate b. Spacing c. Headway d. Speed e. Density 2. Relationships 3. Example
- 3. CEE320 Winter2006 Concepts • Definitions • Volume,Speed, Density relationships • Speed – Space mean speed – Time mean speed
- 4. CEE320 Winter2006 Flow Rate (q) •The number of vehicles (n) passing some designated roadway point in a given time interval (t) • Units are typically vehicles/hour • Flow rate is different than volume t n q =
- 5. CEE320 Winter2006 Spacing • The distance(ft) between successive vehicles in a traffic stream, as measured from front bumper to front bumper
- 6. CEE320 Winter2006 Headway (h) • Thetime (in seconds) between successive vehicles, as their front bumpers pass a given point. ∑= = n i iht 1 h h n q n i i 1 1 == ∑=
- 7.
- 8. CEE320 Winter2006 Speed • Time meanspeed (spot speed) – Arithmetic mean of all instantaneous vehicle speeds at a given “spot” on a roadway section • Space mean speed (u) – The mean travel speed of vehicles traversing a roadway segment of a known distance (d) – More useful for traffic applications
- 9. CEE320 Winter2006 Space Mean Speed •It is the harmonic mean (1/H = 1/a + 1/b + …) • Space mean speed is always less than time mean speed t l n u n i i∑= = 1 1 ( )nnltltlt n t +++= ... 1 2211
- 10. CEE320 Winter2006 Time Mean vs.Space Mean Speed From HCM 2000
- 11. CEE320 Winter2006 Density (k) • Thenumber of vehicles (n) occupying a given length (l) of a lane or roadway at a particular instant • Unit of density is vehicles per mile (vpm). u q l n k ==
- 12. CEE320 Winter2006 Other Concepts • Free-flowspeed (uf) • Jam density (kj) • Capacity (qm) ( ) ( )vehftspacing mivehDensity / 280,5 / = ( ) ( ) ( )sftspeed vehftspacing vehsHeadway / / / = ( ) ( )vehsheadway hrvehrateFlow / 600,3 / =
- 13. CEE320 Winter2006 Speed vs. Density −= j f k k uu1 Density (veh/mile) Speed(mph) kj Jam Density uf Free Flow Speed
- 14. CEE320 Winter2006 Flow vs. Density −= j f k k kuq 2 Density(veh/mile) FLow(veh/hr) kj Jam Density Optimal flow, capacity, qm km Optimal densityUncongested Flow Congested Flow
- 15. CEE320 Winter2006 Speed vs. Flow −= f j u u ukq 2 Flow(veh/hr) Speed(mph) uf Free Flow Speed Optimal flow, capacity, qm Uncongested Flow Congested Flow um
- 16.
- 17. CEE320 Winter2006 Example I-5 over theship canal bridge has 4 lanes in each direction. The northbound capacity is 8200 veh/hr/lane and the free-flow speed is 65 mph. What is the maximum flow rate, maximum density, jam density? If a one-hour vehicle count in the northbound direction for the outside lane gives 7034 vehicles in a non- congested condition, what is the estimated space mean speed of these 7034 vehicles?
- 18. CEE320 Winter2006 Traffic – Timeof Day Patterns 0.00% 1.00% 2.00% 3.00% 4.00% 5.00% 6.00% 7.00% 8.00% 9.00% 1 3 5 7 9 11 13 15 17 19 21 23 Hour of Day PercentofDailyTraffic Rural Cars Business Day Trucks Through Trucks Urban Cars
- 19. From WSDOT 2003Annual Traffic Report
- 20. From WSDOT 2003Annual Traffic Report
- 21. I-405 NE 37thSt GP SB 0 500 1000 1500 2000 2500 12 AM 2 AM 4 AM 6 AM 8 AM 10 AM 12 PM 2 PM 4 PM 6 PM 8 PM 10 PM Estimated Weekday Volume Profile: GP and HOV Lanes (Nov 98) GP HOV
- 22. I-5 NE 45thSt-SB GP SB 0 500 1000 1500 2000 2500 12 AM 2 AM 4 AM 6 AM 8 AM 10 AM 12 PM 2 PM 4 PM 6 PM 8 PM 10 PM Estimated Volume and Speed Conditions (2/17/00)
- 23. I-5 S SpokaneSt GP NB 0 500 1000 1500 2000 2500 12 AM 2 AM 4 AM 6 AM 8 AM 10 AM 12 PM 2 PM 4 PM 6 PM 8 PM 10 PM Estimated GP and HOV Volume and Speed Conditions HOV speed < 45 mph Saturday, July 31, 1999 Data Multicolor = Average GP Lane Gray = HOV Lane
- 24. I-405 NE 37thSt GP NB 0 500 1000 1500 2000 2500 12 AM 2 AM 4 AM 6 AM 8 AM 10 AM 12 PM 2 PM 4 PM 6 PM 8 PM 10 PM 0 10 20 30 40 50 60 70 80 90 100 Estimated Weekday Volume, Speed, and Reliability Conditions (1999) GP HOV
- 25. Time PMAM 0 24 6 8 10 12 2 4 6 8 10 12 Time PMAM 0 2 4 6 8 10 12 2 4 6 8 10 12 405 5 Montlake Blvd. 520 Arboretum 92ndAve. B’vue. Way 148th Ave. NE 60th St. 84th Ave. Lk. Wash. Uncongested, near speed limit Restricted movement but near speed limit More heavily congested, 45 - 55 mph Extremely congested, unstable flow Westbound SR 520Traffic Profile General Purpose Lanes 1997 Weekday Average East bound
- 26. CEE320 Winter2006 Primary References • Mannering,F.L.; Kilareski, W.P. and Washburn, S.S. (2005). Principles of Highway Engineering and Traffic Analysis, Third Edition. Chapter 5 • Transportation Research Board. (2000). Highway Capacity Manual 2000. National Research Council, Washington, D.C.
Editor's Notes
- #6 AMC Pacer and AMC Gremlin
- #10 A harmonic mean is just another way to describe a set of data In this case it is more descriptive for vehicle speeds Example party trick to show you are a knowledgeable engineer You are in a vehicle traveling a total of 10 miles. For the first 5 miles you travel at exactly 40 mph and for the next 5 miles you travel at exactly 60 mph. What is your average speed over the time you spent traveling that 10 miles? Intuitively, you were going at 40 mph for longer than you were going at 60 mph so your average velocity for the entire trip is going to be less than the arithmetic mean of 50 mph It’s 48 mph by harmonic mean distance = speed * time 5 miles at 40 mph = 7.5 minutes 5 miles at 60 mph = 5 minutes weighted average = (40(7.5) + 60(5))/(7.5 + 5) = 48 mph Example 5 vehicles over a given 1 mile section take 1.0, 1.2, 1.5, 0.75 and 1.0 minutes respectively Average travel time = 5.45/5 = 1.09 minutes = 0.0182 hours Therefore, average speed = 1 mile/0.0182 hours = 55.05 mph
- #12 Occupancy is often used as a surrogate
- #13 Occupancy often used as a surrogate to density because it’s easier to measure Density is difficult to measure because you have to essentially image a long stretch of road Occupancy and density are correlated by not perfectly
- #16 Lots of measurements in the top part, a few in the queue part and a few in the congested part Segment 1 = top part = uncongested Segment 2 = straight part = queue discharge Segment 3 = bottom part = within a queue
- #17 Occupancy is a surrogate for density since density is often difficult to measure
- #18 Maximum flow rate, qm = 8200 veh/hr as given At maximum flow: dq/dk = uf(1-2km/kj) = 0 Since uf is not zero, 1-2km/kj = 0 Therefore km = kj/2 Similarly, um = uf/2 Therefore, um = 65/2 = 32.5 mph. Therefore, maximum density, km = qm/um = 8200/32.5 = 252.31 vehicles/mile kj = 2*km = 2*(252.31) = 504.62 veh/mile/lane Using the speed-flow relationship: q = kj(u – u2/uf) Solve for q = 7034 = 504.62(u – u2/65) 13.94 = u – u2/65 906.06 = 65u – u2 u2 – 65u + 906.06 = 0 u = 44.7 or 20.2 mph Choose 41.6 since this is the higher of the two and the observed flow is less than qm so we know we are not in the congested area of the curve
- #19 Truck travel is driven by business needs. Passenger car travel is driven by personal needs. These are different. Thus, trucks often move at different times than cars.
- #22 Just north of the SR 520 interchange This graph shows a good example of how HOV and GP volumes change over time on I-405 in the south end. An interesting aspect of I-405 is that usage stays high throughout the day. At this location (near Kennydale), the two GP lanes stay fairly full throughout the day.
- #23 Effects of an incident around 2pm This picture shows the impact of a rendering truck accident on I-5 in Seattle. You can see the traditional morning congestion, and the afternoon congestion caused by the accident. You can really see the loss of facility capacity (and thus throughput), and the duration of the slow speeds,long after the accident has been cleared. This type of picture is an excellent tool for describing to decision makers and the general public why incident response is needed, as well as serving as an excellent tool for examining the effectiveness of those measure you do implement.
- #24 In this case, we plotted two different lanes in order to show how HOV lanes work on weekends in Seattle. The number of legal “carpools” is high on weekends, but people don’t end to use those lanes unless the facility gets congested. This graphic illustrates how the GP lane and HOV lane volumes converge, once congestion occurs.
- #25 This graphic compares HOV and GP lane performance. Only the GP lane is color coded and the congestion histogram applies only to the GP lane. At this location, we can see the effect persistent congestion has on GP volumes. It also shows very well, how GP congestion can help encourage HOV use. This site also shows how HOV lane volumes can be reasonably high (if not equal to GP lane volumes) even during the middle of the day.