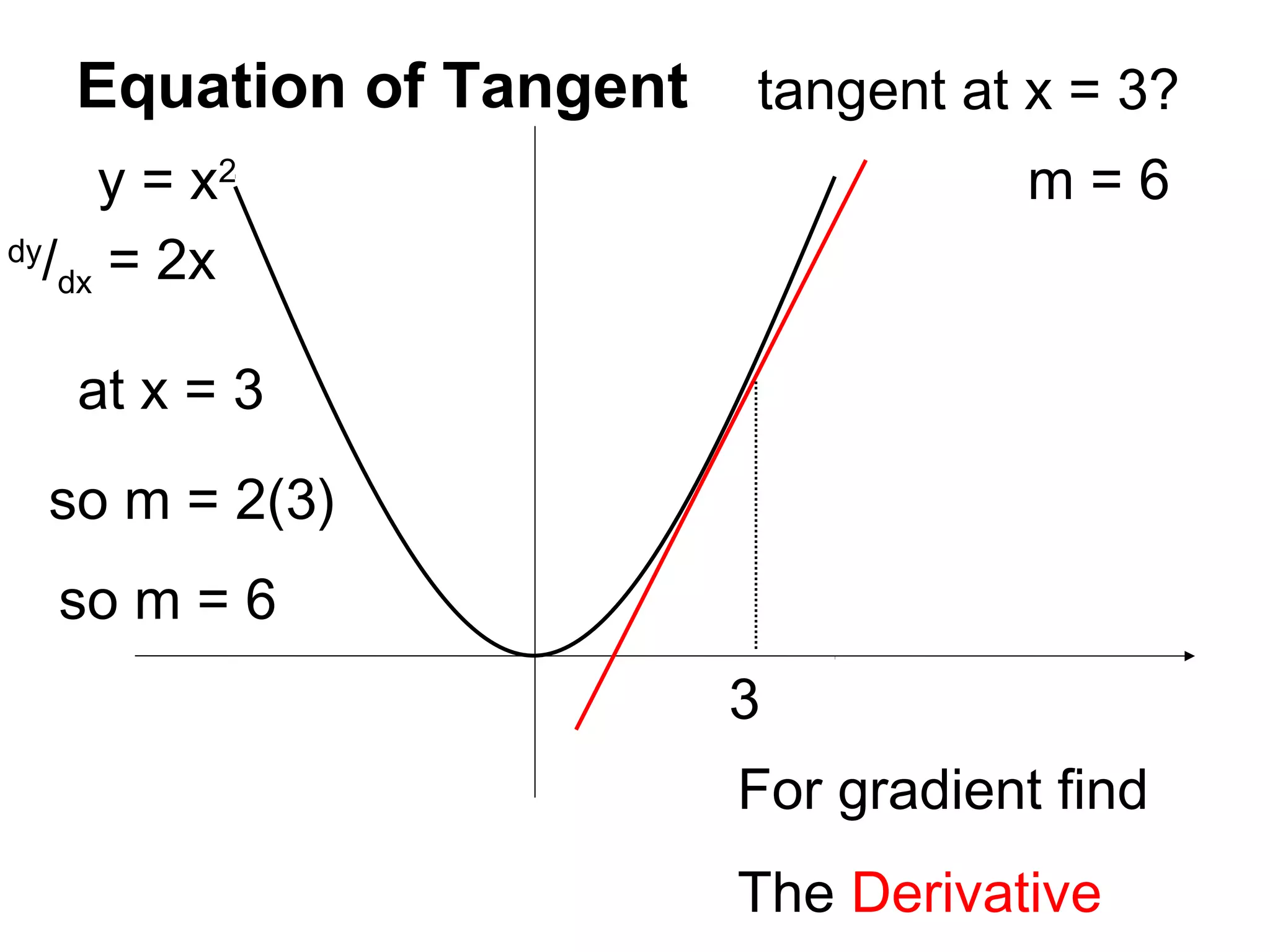
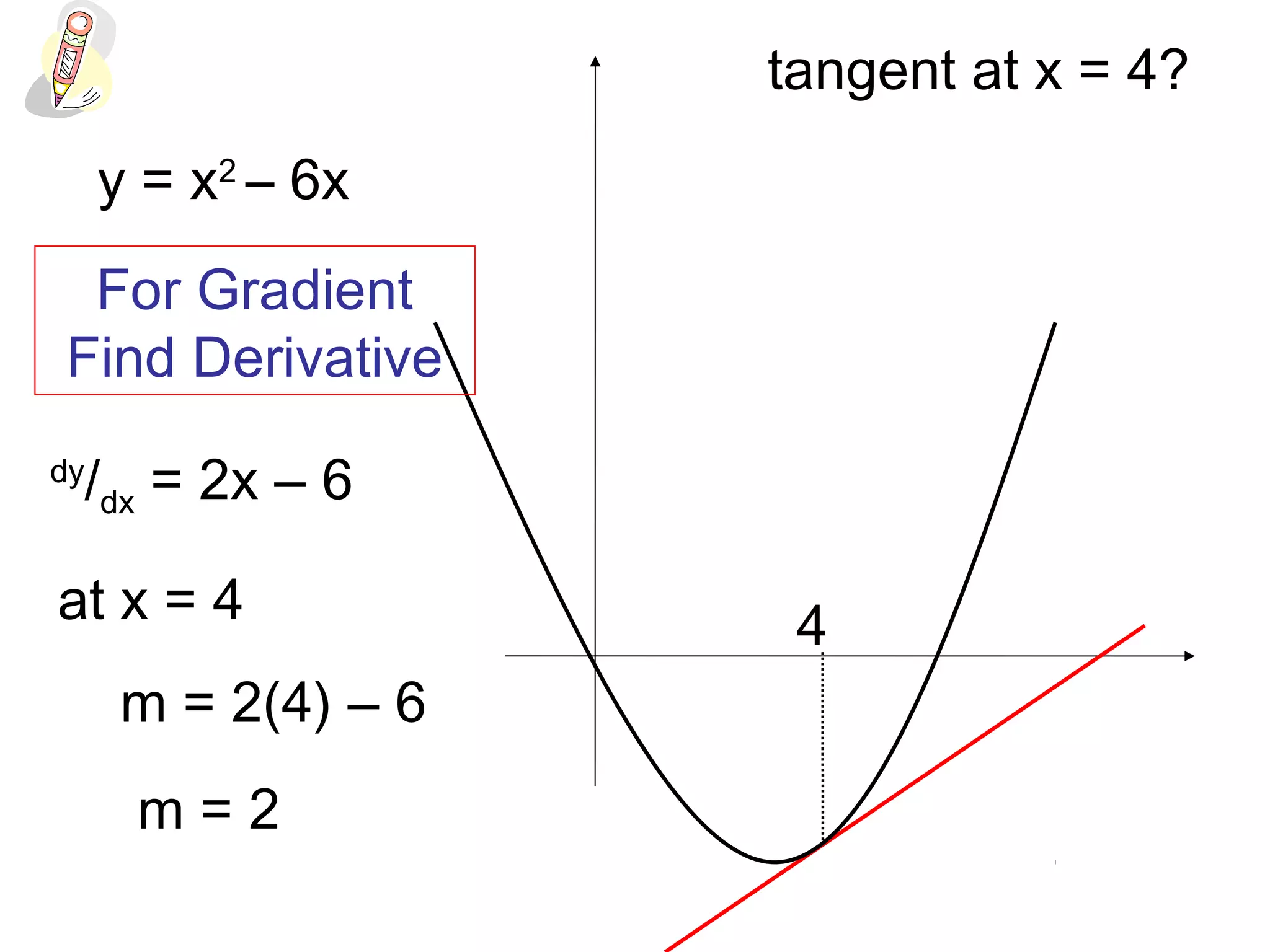
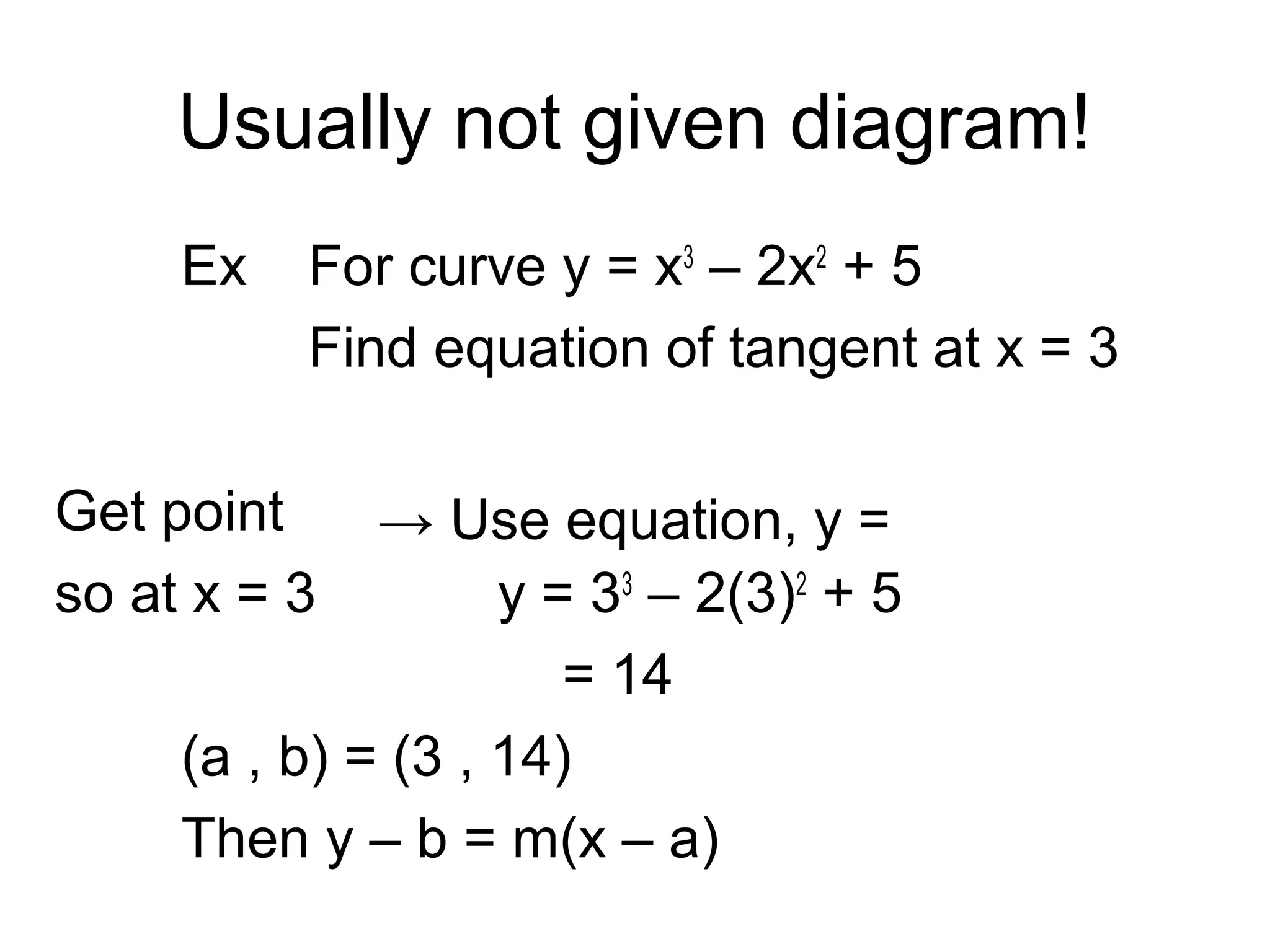This document discusses how to find the equation of a tangent line to a curve at a given point. It explains that you need to find the derivative to get the slope (m) of the tangent line, use the original equation to find the y-coordinate (b) of the point, and then plug those values into the equation for a line, y - b = m(x - a), to get the equation of the tangent line. It provides examples finding the derivatives, slopes, points and tangent equations for curves like y = x^2, y = x^3 - 2x^2 + 5, and y = x^3 - 7x - 3 at given x-values.

1. Block 1
Equations of Tangents

2. What is to be learned?
• How to use differentiation to find all the
stuff we need to get equation of a tangent.

3. Differentiation gives us
• Gradients of tangents to curves
• Rates of change

4. Gradient of Tangent
Curve y = 4x2
– 6x
Gradient of tangent at x = 5?
Find derivative
dy
/dx = 8x – 6
Substitute x value
= 8(5) – 6
= 34
m

5. Gradient of Tangent
Curve y = x3
– 8x
Gradient of tangent at x = 4?
Find derivative
dy
/dx = 3x2
– 8
Substitute x value
= 3(4)2
– 8
= 40
m

6. tangent at x = 3?
For Equation need
gradient m
point (a , b)
3
y = x2
Equation of Tangent

7. y = x2
tangent at x = 3?
For gradient find
The Derivative
dy
/dx = 2x
at x = 3
so m = 6
3
Equation of Tangent
m = 6
so m = 2(3)

8. y = x2
tangent at x = 3?
Point?
(3 , ?)
Need y
coordinate
3
Equation of Tangent
m = 6

9. y = x2
tangent at x = 3?
Point?
at x = 3 (a , b) = (3 , 9)
Need y
coordinate
3
Equation of Tangent
(3 , ?)
m = 6
y = 32
y = 9 9

10. y = x2
tangent at x = 3?
m = 6, (a , b) = (3 ,9) Need y
coordinate
use y – b = m(x – a)
3
Equation of Tangent
(3 , ?)
m = 6
9
(a , b) = (3 , 9)

11. Usually not given diagram!
Ex For curve y = x3
– 2x2
+ 5
Find equation of tangent at x = 3
Get m
dy
/dx = 3x2
– 4x
so at x = 3 m = 3(3)2
– 4(3)
= 15
→ Need Derivative

12. Usually not given diagram!
Ex For curve y = x3
– 2x2
+ 5
Find equation of tangent at x = 3
Get point
so at x = 3 y = 33
– 2(3)2
+ 5
= 14
(a , b) = (3 , 14)
Then y – b = m(x – a)
→ Use equation, y =

13. Equations of Tangents
For Equation need
• gradient m
• point (a , b)
Find Derivative
Use original equation
Then use y – b = m(x – a)

14. tangent at x = 4?
4
y = x2
– 6x

15. y = x2
– 6x
tangent at x = 4?
dy
/dx = 2x – 6
at x = 4
m = 2(4) – 6
m = 2
4
For Gradient
Find Derivative

16. y = x2
– 6x
tangent at x = 4?
(4 , ?)
Need y
coordinate
4
For Point
Use Original Equation
at x = 4
(a , b) = (4 , -8)
y = 42
– 6(4)
= -8
use y – b = m(x – a)

17. Key Question
Ex For curve y = x3
– 7x – 3
Find equation of tangent at x = 2
Get m dy
/dx = 3x2
– 7
so at x = 2 m = 3(2)2
– 7
= 5
Get point
so at x = 2 y = 23
– 7(2) – 3
= -9
m = 5 (a , b) = (2 , -9)
→ y + 9 = 5(x – 2)