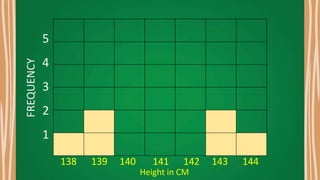
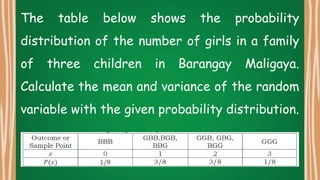
This document appears to be a lesson plan on probability and statistics that includes: 1. Definitions of key terms like normal random variables, mean, mode, and standard deviation. 2. Examples of calculating mean, variance, and standard deviation from probability distributions. 3. Properties and characteristics of the normal probability distribution curve including that it is bell-shaped and symmetrical around the mean. 4. Examples of comparing normal distribution curves based on differences in their means and standard deviations. 5. Practice problems for students involving calculating probabilities and expected values from scenarios like raffles and games of chance.

1. Dianne Reichel T. Ronio
Teacher III

4. New Normal
Classroom Rules

6. Checking of
Attendance

7. After going through this lesson, you
are able to:
1. define a normal random variable;
2. illustrate a normal random
variable and its characteristics;

8. After going through this lesson, you
are able to:
3. listen attentively during class
discussion;
4. participate actively in activities;
and

9. After going through this lesson, you
are able to:
5. appreciate the importance of the
lesson being discussed.

10. Review!!!

11. Read the following
statements carefully and
determine whether it is
TRUE or FALSE.

12. Probability is the value
greater than or equal to
zero but less
than or equal to one.

13. Discrete variables are
the infinite numerical
values like heights,
weights, distance and
length

14. 34% is also
equal 0.34.

15. Mean, mode and
standard deviation
are the measures
of central
tendency.

16. Mean is equal to the
summation of scores
divided by the
number of cases.

18. The distribution of the
height (X) in centimeter
(cm) of the 16 teachers of
Naic Integrated NHS-
SHS was presented on the
table. Construct a
histogram for the random
variable (X).

19. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

20. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

21. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

22. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

23. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

24. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

25. 5
4
3
2
1
138 139 140 141 142 143 144
FREQUENCY
Height in CM

26. Normal Probability
Distribution
• is a probability distribution of
continuous random variables.

27. Normal Probability
Distribution
• It is used to describe the
characteristics of populations and
help us visualize the inferences we
make about the population.

28. Normal Probability
Distribution
• It also used to determine the
probabilities and percentile of
the continuous random
variables in the distribution.

29. Properties of Normal Curve
1. The normal curve is bell-
shaped.
2. The curve is
symmetrical about its
center.

30. Properties of Normal Curve
3. The mean, median, and mode
coincide at the center.
4. The width of the curve is
determined by the standard
deviation of the distribution.

31. Properties of Normal Curve
5. The tails of the curve are plotted
in both directions and flatten out
indefinitely along the horizontal axis.
The tails are thus asymptotic to the
baseline
6. The total area under a normal
curve is 1

32. Below is the graph of the normal curve

33. A normally distributed random variable with a mean μ =
0 and standard deviation ơ = 1 is called a standard
normal variable

34. The shape of a normal curve is based on the
two given parameters, the mean and the
standard deviation of the distribution.
When comparing two distributions each
described by the normal curve, the following
are the three situations based on the said
parameters

35. When the means are not equal, but the standard
deviations are equal. (μ1 ≠ μ2 ; ơ1 =ơ2 ), the
curves have a similar shape but centered at
different points

36. When the means are equal, but the standard deviations
are not equal. (μ1 = μ2 ; ơ1 ≠ ơ2 ), the curves are
centered at the same point but they have different
height and spreads

37. When the means are different and the standard
deviations are also different (μ1≠ μ2 ; ơ1 ≠ ơ2 ), the
curves are centered at different points and vary in
shapes

38. Analyze the following figures and
describe each by identifying
whether they have the same or
different mean and standard
deviation.

39. Check each figure and
answer the questions that
follows.

40. After going through this lesson, you
are able to:
1. Calculate the mean and the
variance of a discrete random
variable;

41. Recall the formula for:
1.Expected Value or Mean Value
2.Variance
3.Standard Deviation

42. The table below shows the probability
distribution of the number of girls in a family
of three children in Barangay Maligaya.
Calculate the mean and variance of the random
variable with the given probability distribution.

43. Game of Chance

44. Game of Chance

45. Questions:
1. If you are Cardo, would you buy a raffle ticket?
Why?
2. If Cardo decided to buy five tickets, what is the
probability that he would win the prize if 1000 tickets
were sold?
What is the probability that Cardo will lose the bet?
3. How much money will Cardo gain if he wins the
prize?

46. Questions:
4. How much money will be wasted if he will not
win the prize and he buy one ticket?
5. What if 1000 tickets were purchased by
different individuals, what is the expected value
of buying one ticket?
6. How would you describe Romulo as a friend?

47. Seatwork 13:Raffle Tickets Problem

48. Seatwork 13:Raffle Tickets Problem

49. Seatwork 14: Raffle for a Cause

50. Seatwork 15: Roulette Wheel

51. Seatwork 16: Insurance Investment

52. The negative value (in expected value)
means that one loses money on the
average.
Having this knowledge, you can now
make a wise decision.

53. But remember, important things should be
prioritized. If you can afford to buy tickets
without sacrificing your essential needs. It is
okay to take a chance sometimes. You should also
consider saving money for future use, because
not every day you have enough funds, having
extra money would be a great help in times of
need.

54. Assessment
Direction: Choose the letter of the best
answer.