The document discusses techniques for finding the slope of a tangent line to a function at a given point using derivatives. It provides examples of finding the slope for various functions, including polynomials, trigonometric functions, and implicitly defined functions, using the definition of derivative and rules like the product rule. Approximations of slope using finite differences are also covered. Guidelines for performing implicit differentiation are outlined.

1. Derivative Application Group Members: Baba Qazi; Joey Lee; Tam Dong

2. Tangent line equation y=m(x-x 1 )+y 1 What do you need to find a tangent line equation? m= Slope of the tangent line (x,y): coordinate of a point (x 1 ,y 1 ): coordinate of another point The slope and a point

3. Ex: If f(x)=x 2 +2. Determine the slope of the tangent line to f(x) at x=5. 1. f(x)=x 2 +2 =>f’(x)=2x => f’(5)=10 2. f(5)=25+2=27 3. y=m(x-x 1 )+y 1 4. y=10(x-5)+10 Derivative Applications of tangent line

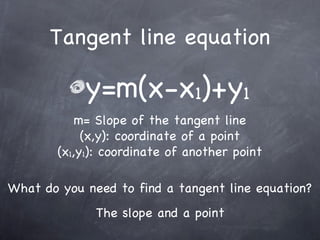
4. Derivative Applications of tangent line (cont) Ex: If f(x)=sin(x)cos(x). Determine the slope of the tangent line to f(x) at x=π/4. 1.f(x)=sin(x)cos(x) => product rule 2.f(x)=sin(x);f’(x)=cos(x) | g(x)=cos(x);g’(x)=-sin(x) 3.f’(x)= -sin(x)sin(x)+2cos(x) = 2cos(x)-2sin(x) 4.f(π/4)=sin(π/4)cos(π/4)=(√2/2)(√2/2)=1 5.f’(π/4)=2cos(π/4)-2sin(π/4)=2(√2/2) - 2(√2/2)=0 6.y=m(x-x 1 )+y 1 => y=0[x-(π/4)]+1

5. Slope at a point The derivative of the function at a point is the slope of the line tangent to the curve at the point, and is thus equal to the rate of change of the function at that point.

6. Slope at a point Ex: Find the instantaneous rate of change of y=6x 2 when x=3 d/dx=12x => f’(3) = 12.3= 36

7. Approximation Approximation is used to determine the slope of the equation by (∆y/∆x) Examples Forward quotient: (8-6)\(3-2)= 2 Backward quotient: (6-4)\(2-1)= 2 Symmetric quotient: (8-4)\(3-1)= 2 x 1 2 3 y 4 6 8

8. Implicit Differentiation The purpose of using implicit differentiation is when it is very difficult to express y as a function respect to x Derive: y 3 + y 2 - 5y -x 2 = -4 1. y 3 + y 2 - 5y -x 2 = -4 2. (d/dx) [y 3 + y 2 - 5y -x 2 ] = (d/dx) -4 3. 3y 2 (dy/dx) + 2y(dy/dx) - 5(dy/dx) - 2x = 0 4. (dy/dx)(3y 2 + 2y -5) = 2x 5. (dy/dx) = 2x/(3y 2 + 2y -5)

9. Guidelines for Implicit Differentiation 1. Differentiate both sides of the equation with respect to x. 2. Collect all terms involving dy/dx on the left side of the equation and move all other terms to the right side of the equation. 3. Factor dy/dx out of the left side of the equation 4. Solve for dy/dx