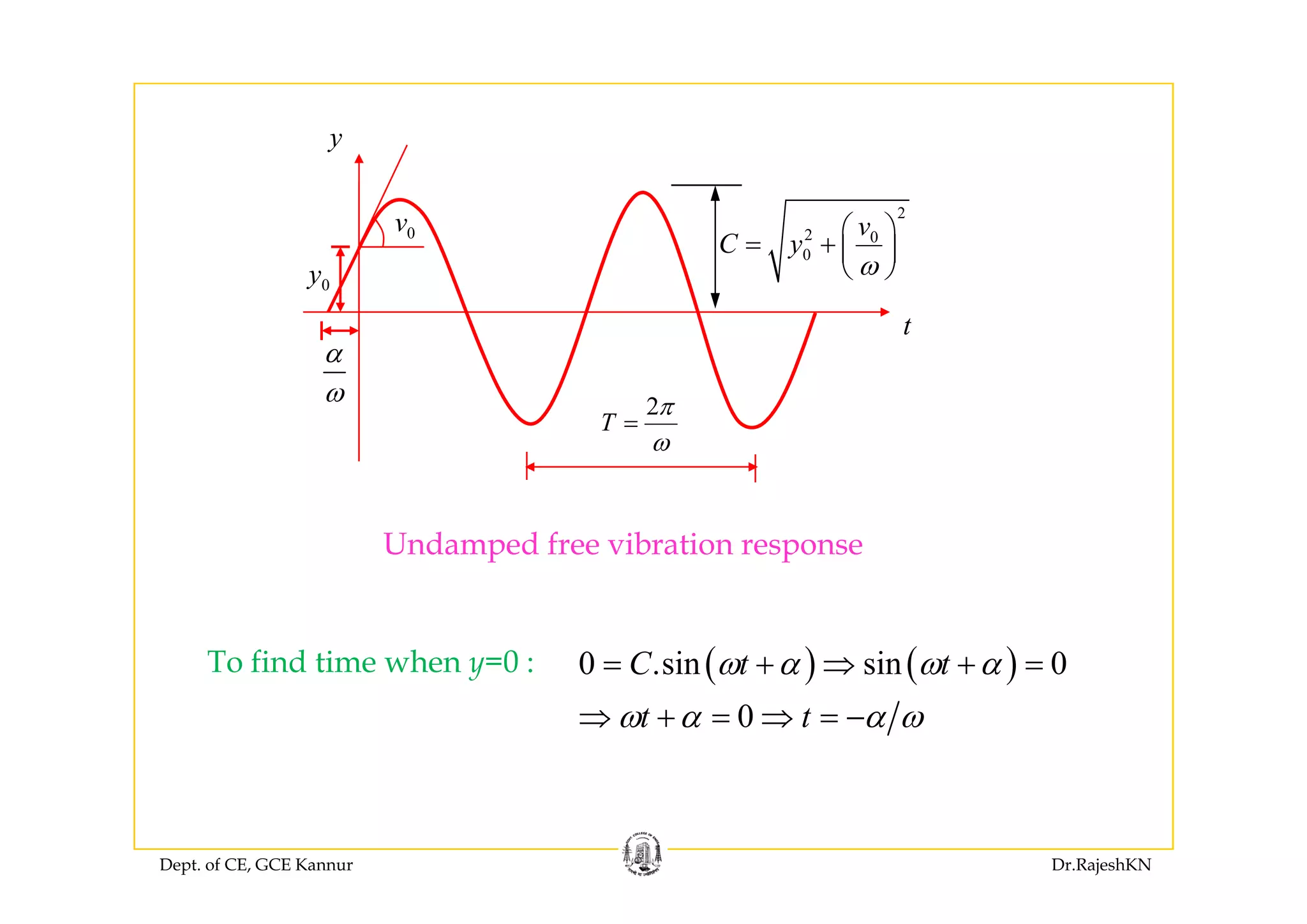
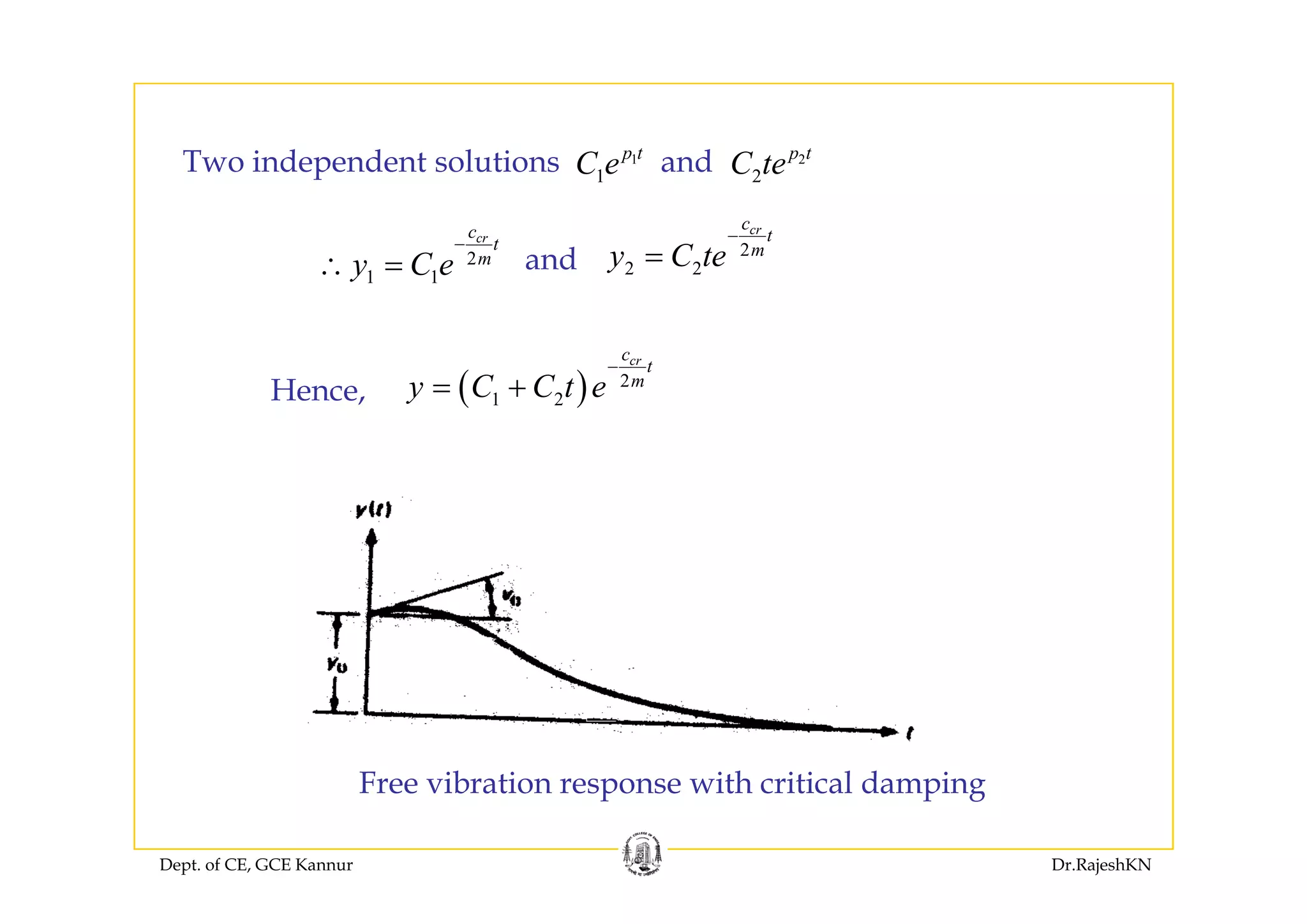
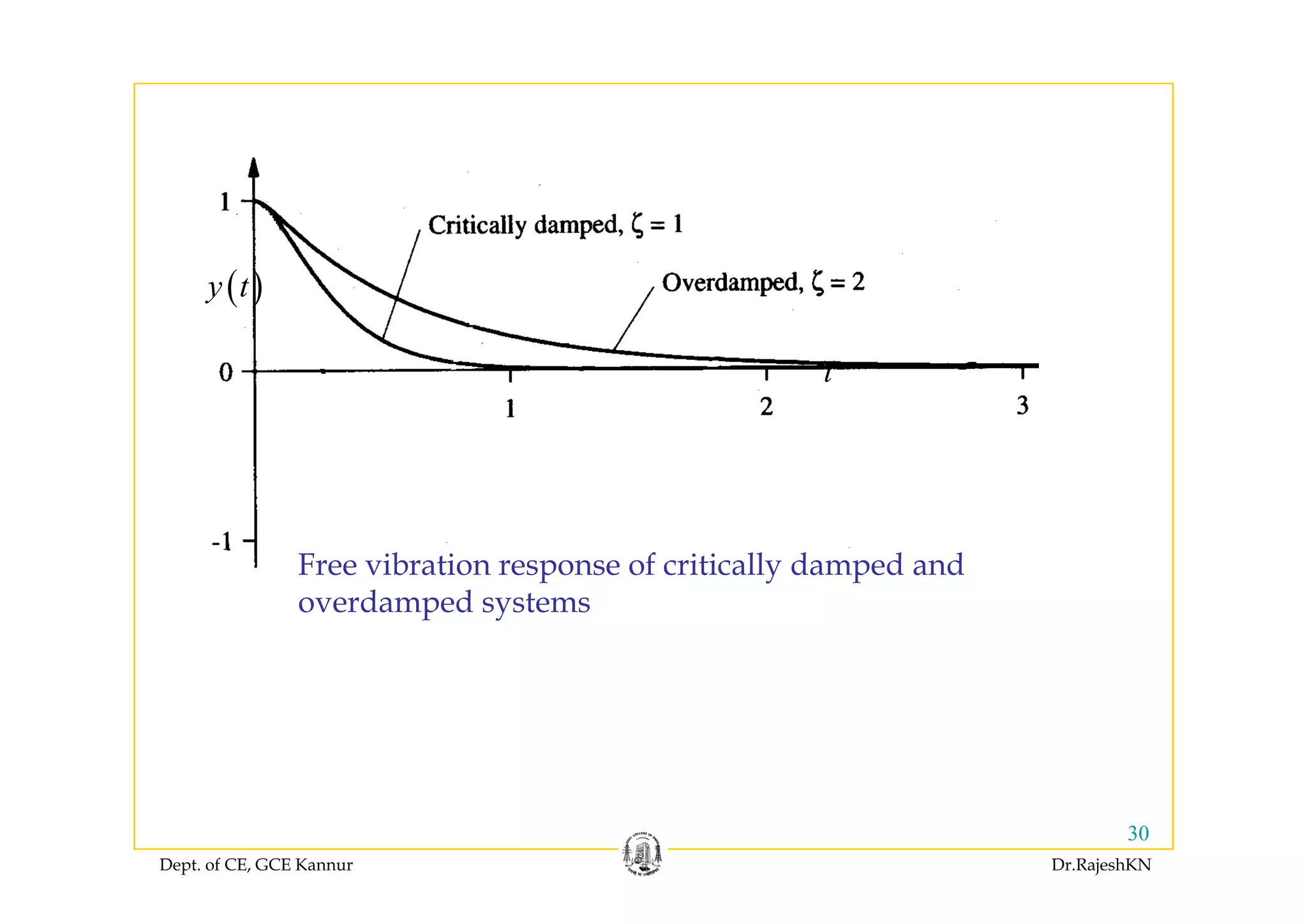
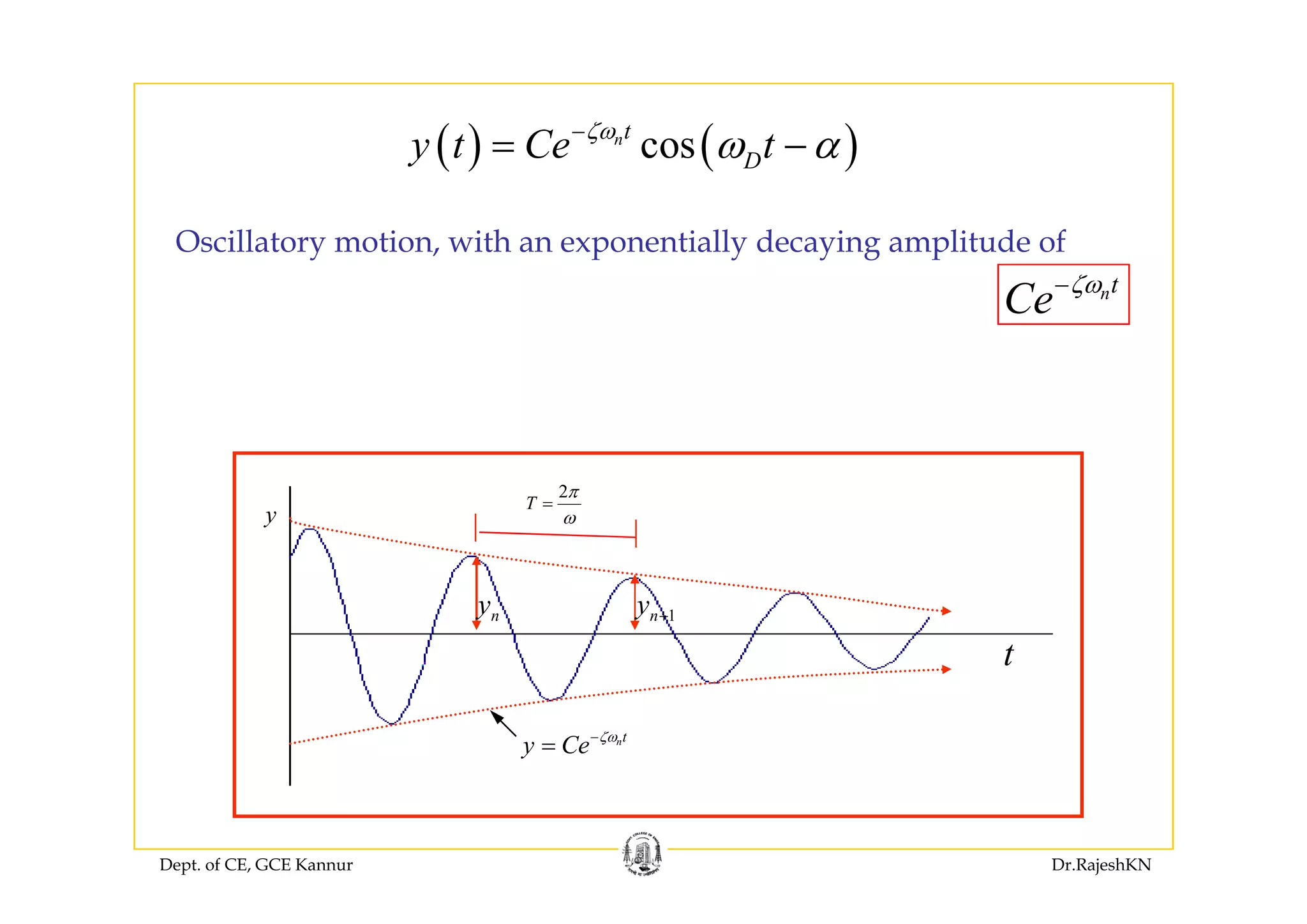
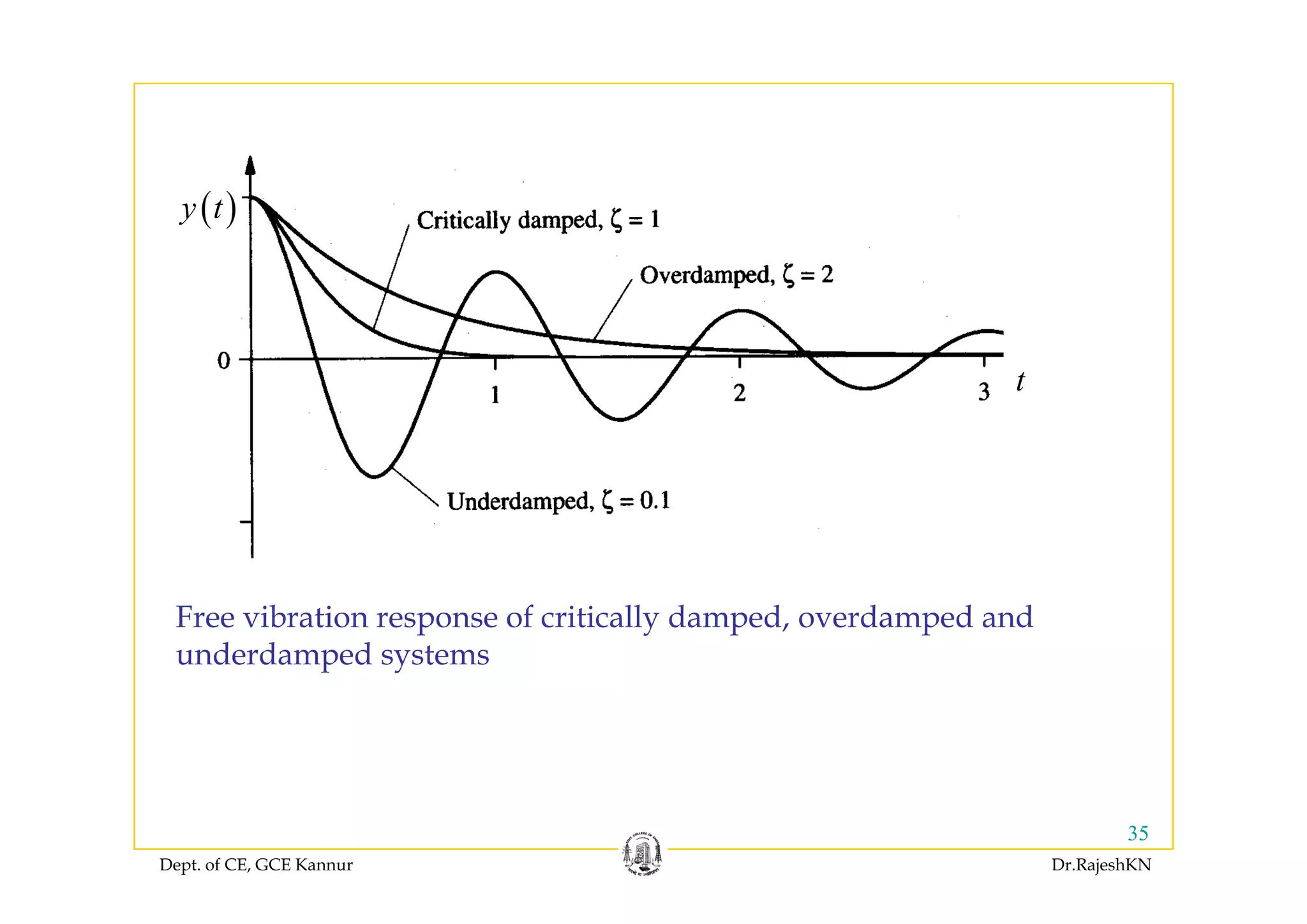
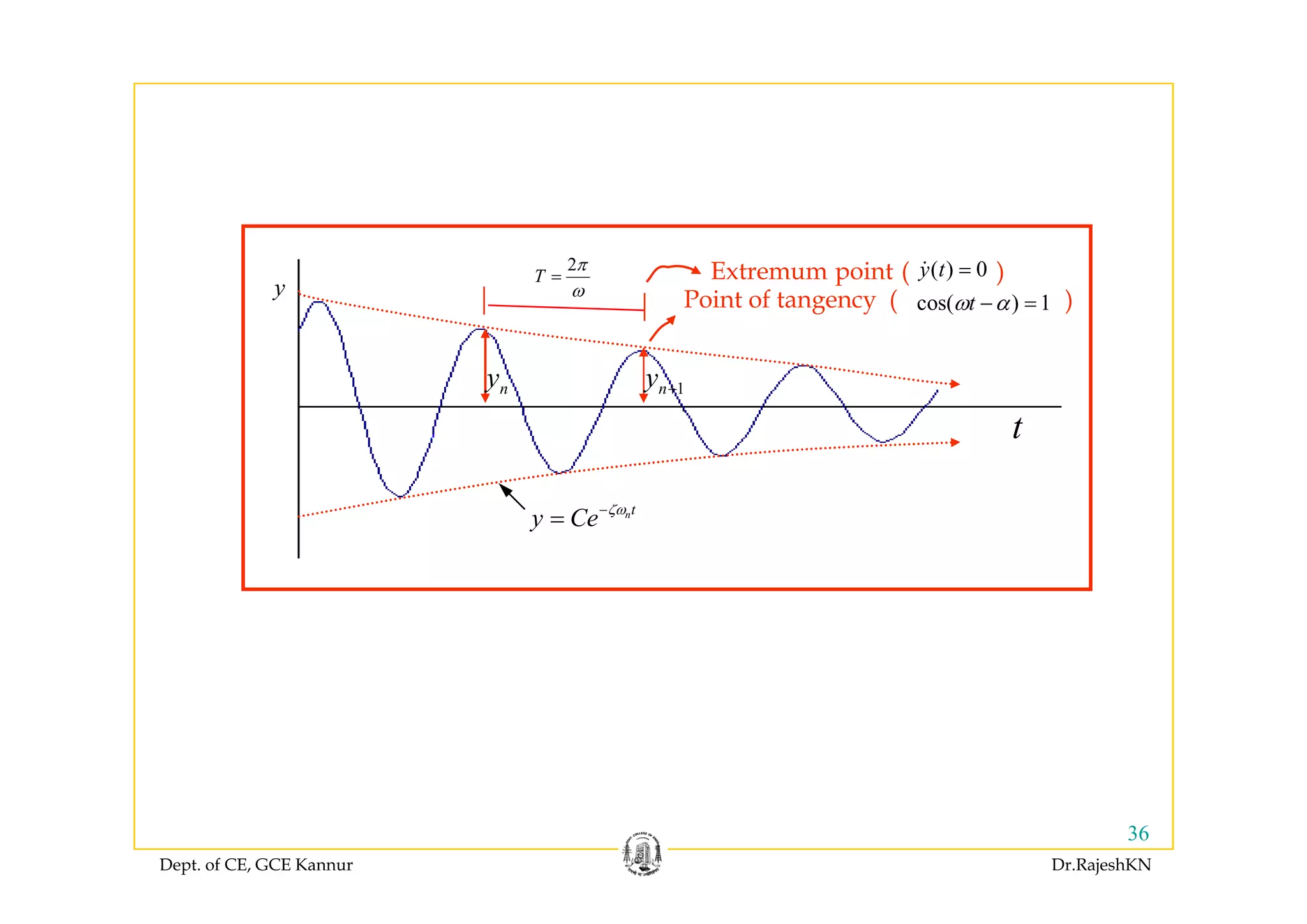
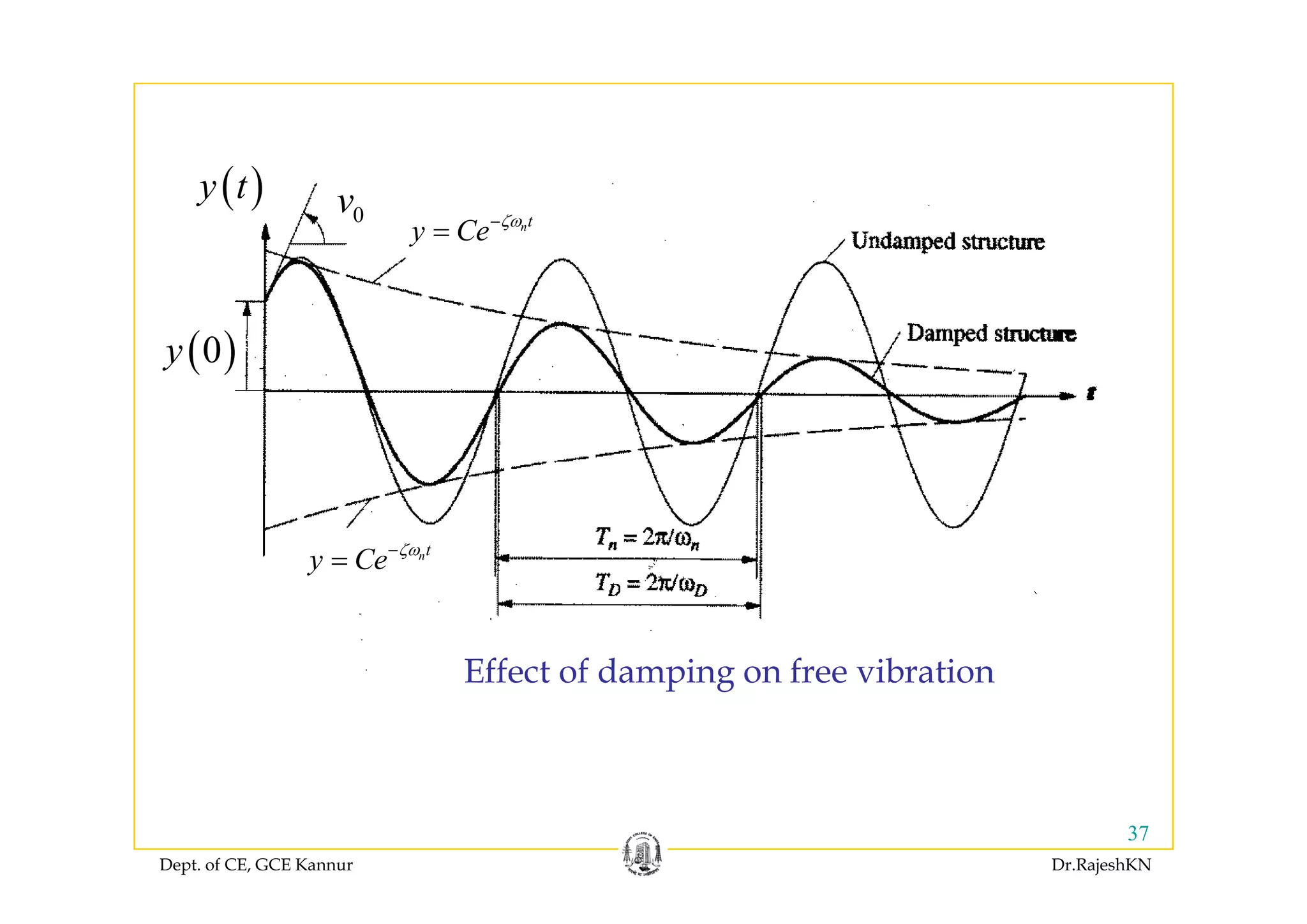
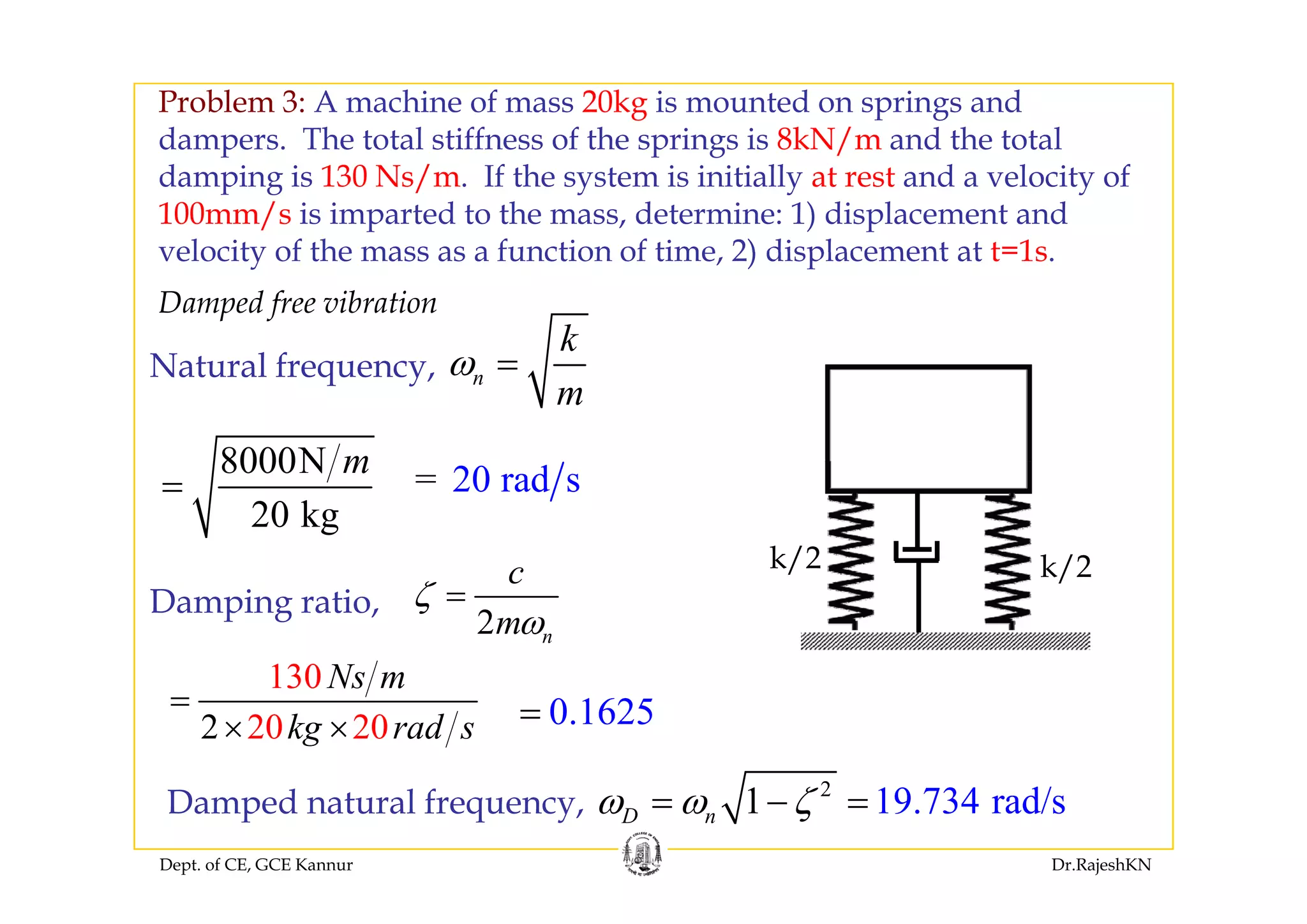
This document provides an overview of structural dynamics and free vibration analysis of single degree of freedom systems. It defines key concepts like natural frequency, damping, and logarithmic decrement. Methods for analyzing undamped and damped free vibration are presented. Examples show how to calculate the natural frequency, time period, amplitude, and displacement as a function of time for undamped systems subjected to initial displacement or velocity conditions. Analysis of damped systems models the response as a decaying exponential function.






















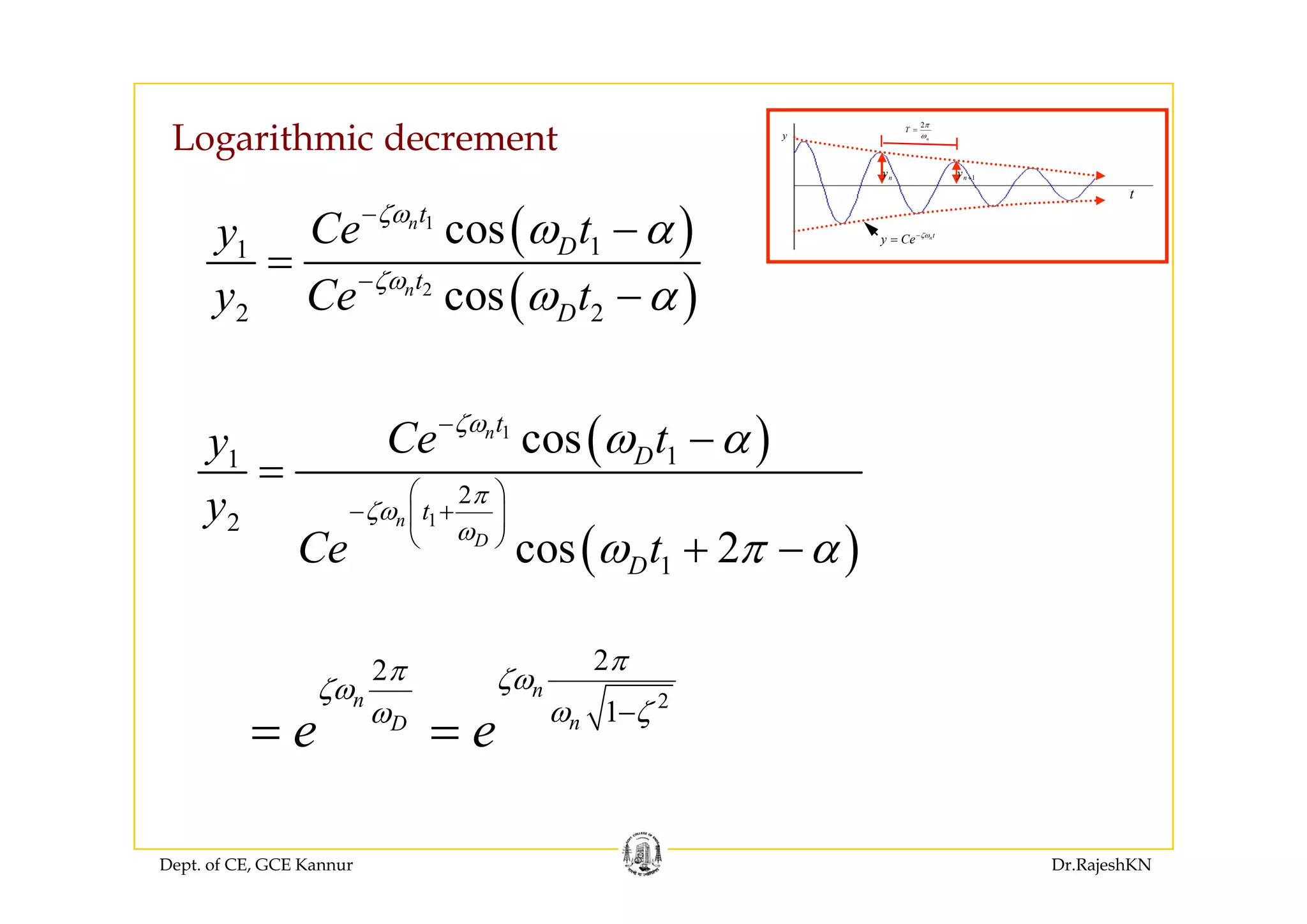
![( ) ( )n D Dt i t i t
t A Aζω ω ω− −
+( ) ( )1 2
n D Di t i t
y t e Ae A eζ ω ω
= +
cos sinDi t
D De t i tω
ω ω= ±But
( ) ( ) ( )1 2 1 2cos sinnt
D Dy t e A A t i A A tζω
ω ω−
∴ = + + −⎡ ⎤⎣ ⎦
( ) [ ]i e cos sinnt
y t e A t B tζω
ω ω−
= +( ) [ ]i.e., cos sinn
D Dy t e A t B tζ
ω ω= +
Dept. of CE, GCE Kannur Dr.RajeshKN](https://image.slidesharecdn.com/module4-sdynamics-rajeshsir-140806045959-phpapp02/75/Module4-s-dynamics-rajesh-sir-32-2048.jpg)



















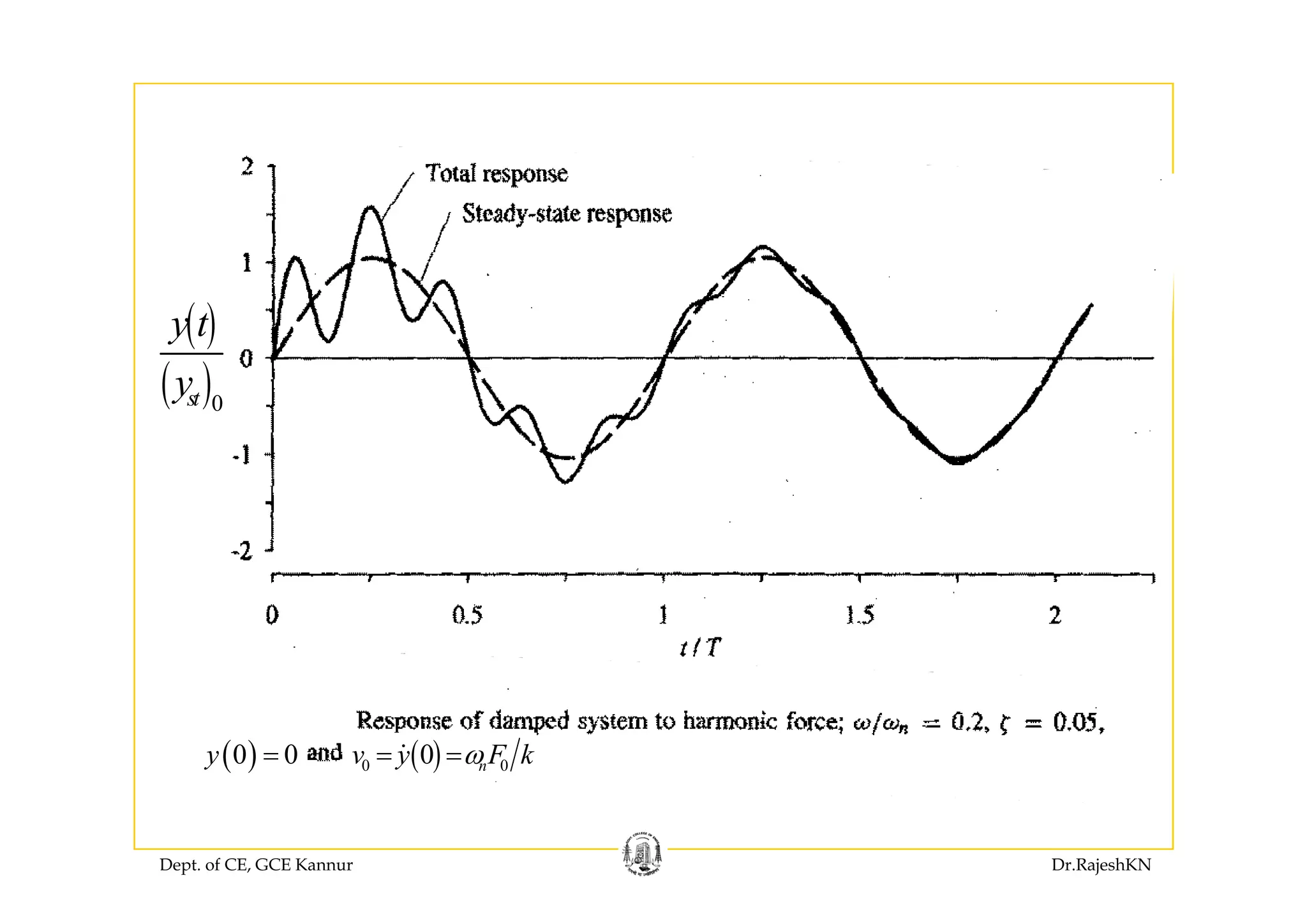
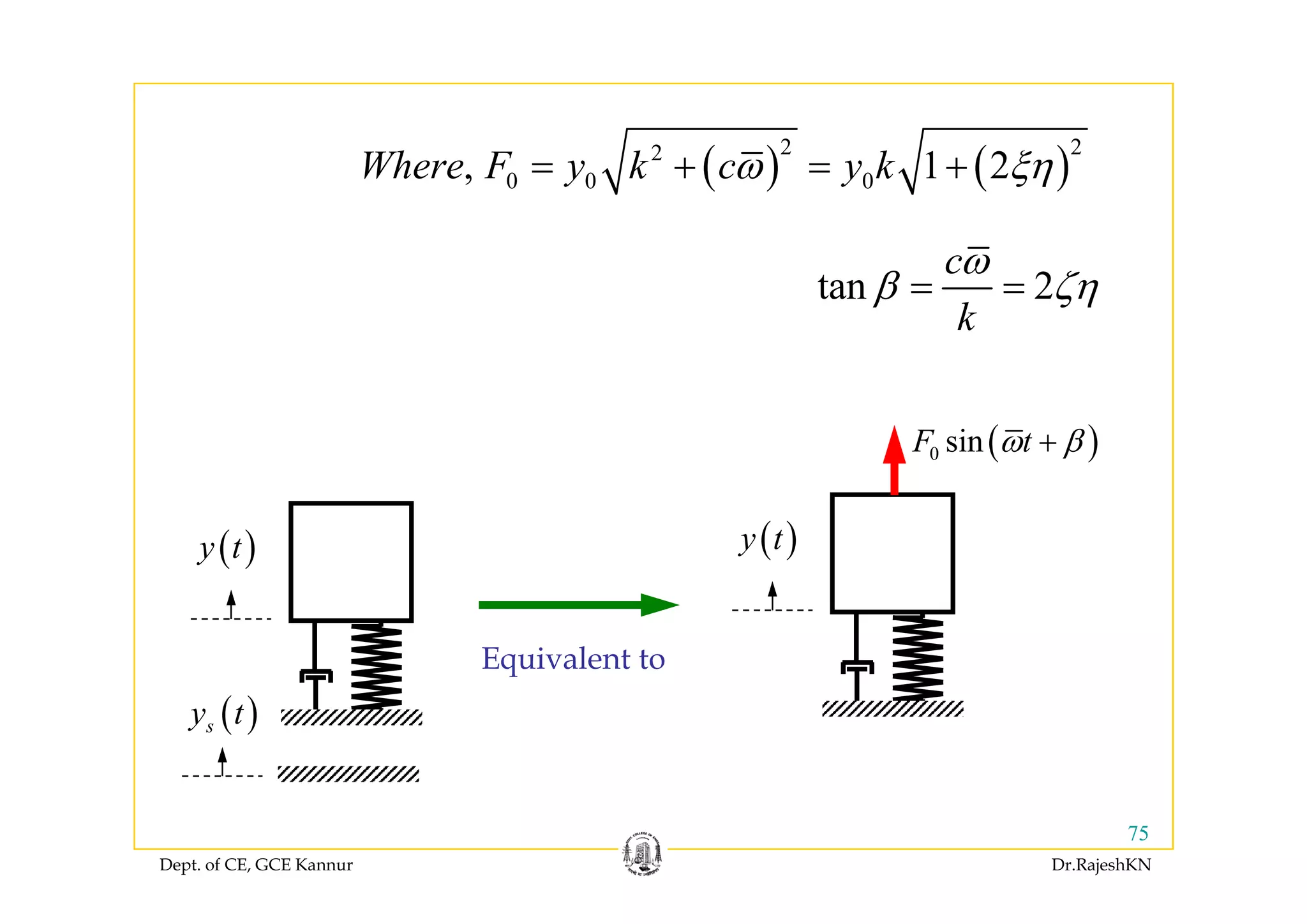
![Response of damped system to harmonic excitation
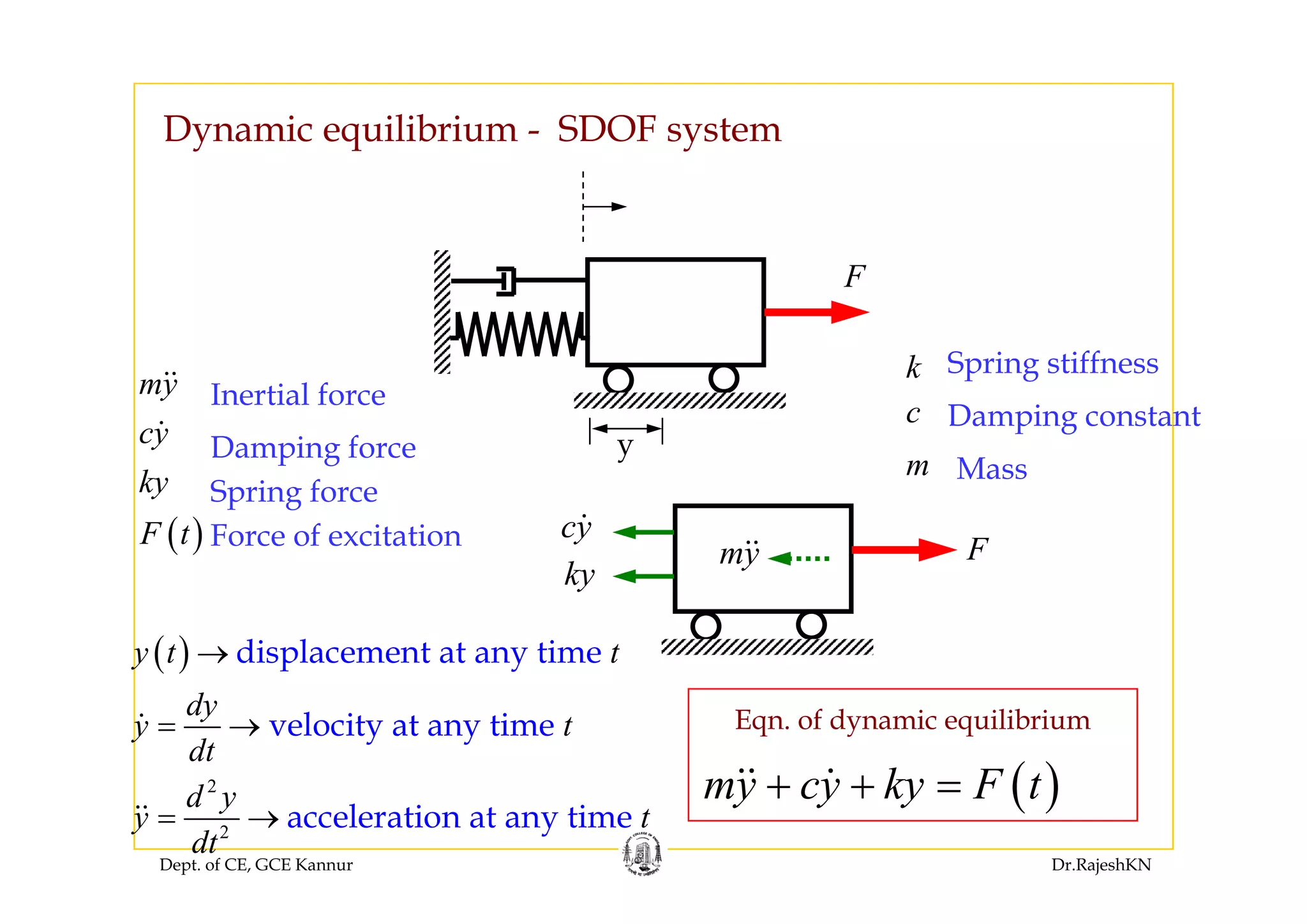
( )y t
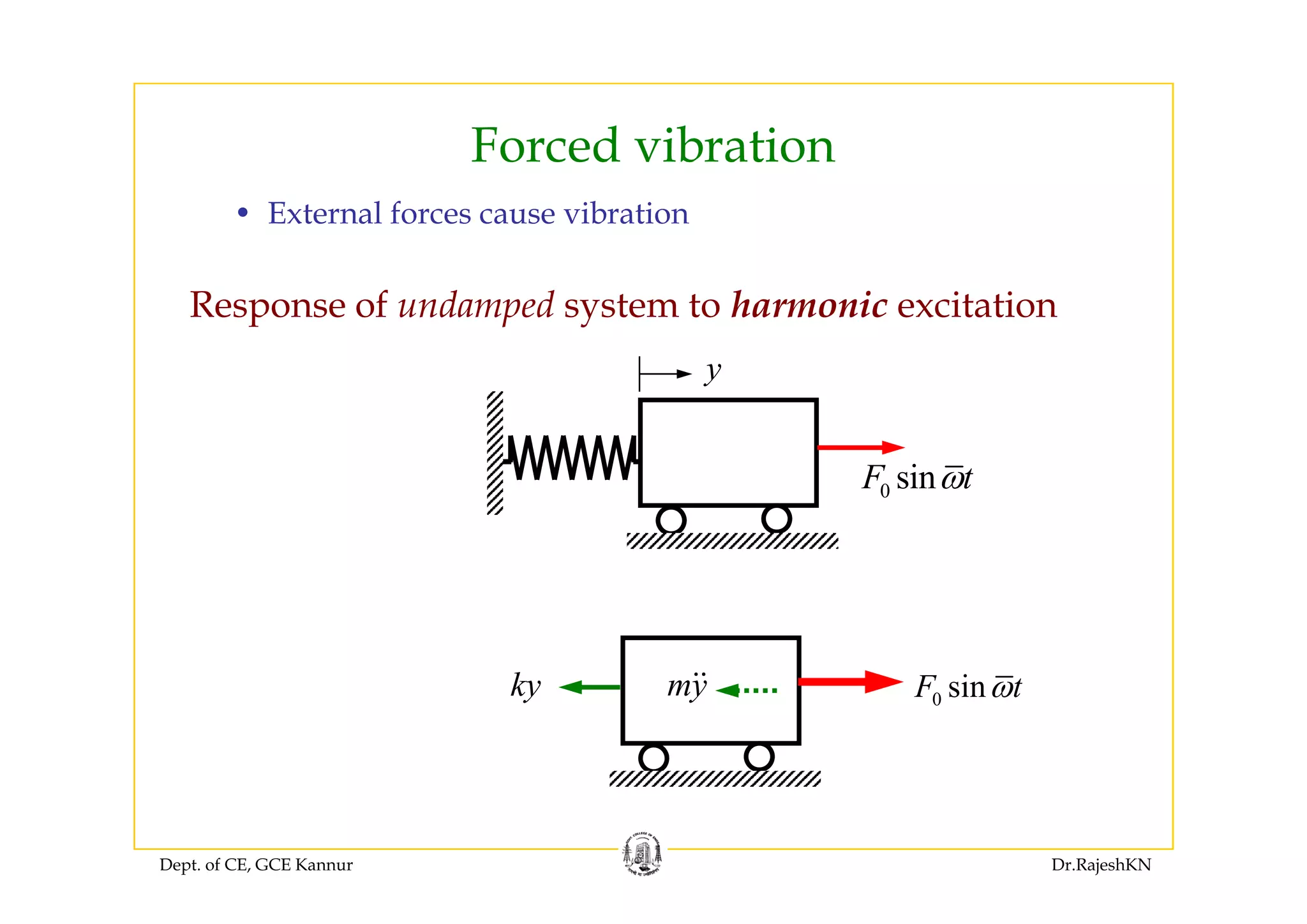
0 sinmy cy ky F tω+ + =
B
0 sinF tω
( ) ( ) ( )
B
( ) ( ) ( )c py t y t y t= +Solution is
( )t C li t l ti S l f h( )cy t Complimentary solution – Soln of homogeneous eqn
0my cy ky+ + =
( ) [ ]cos sinnt
c D Dy t e A t B tζω
ω ω−
= +
Dept. of CE, GCE Kannur Dr.RajeshKN
• But damping will cause this part to die out -> Transient response](https://image.slidesharecdn.com/module4-sdynamics-rajeshsir-140806045959-phpapp02/75/Module4-s-dynamics-rajesh-sir-60-2048.jpg)


![( )
( ) ( )
( ) ( )
[ ]
2 22
0
2 22
cos sin sin cosp
F k m c
y t t t
k
ω ω
φ ω φ ω
ω ω
− +
= −
+( ) ( )k m cω ω− +
22
k mω−
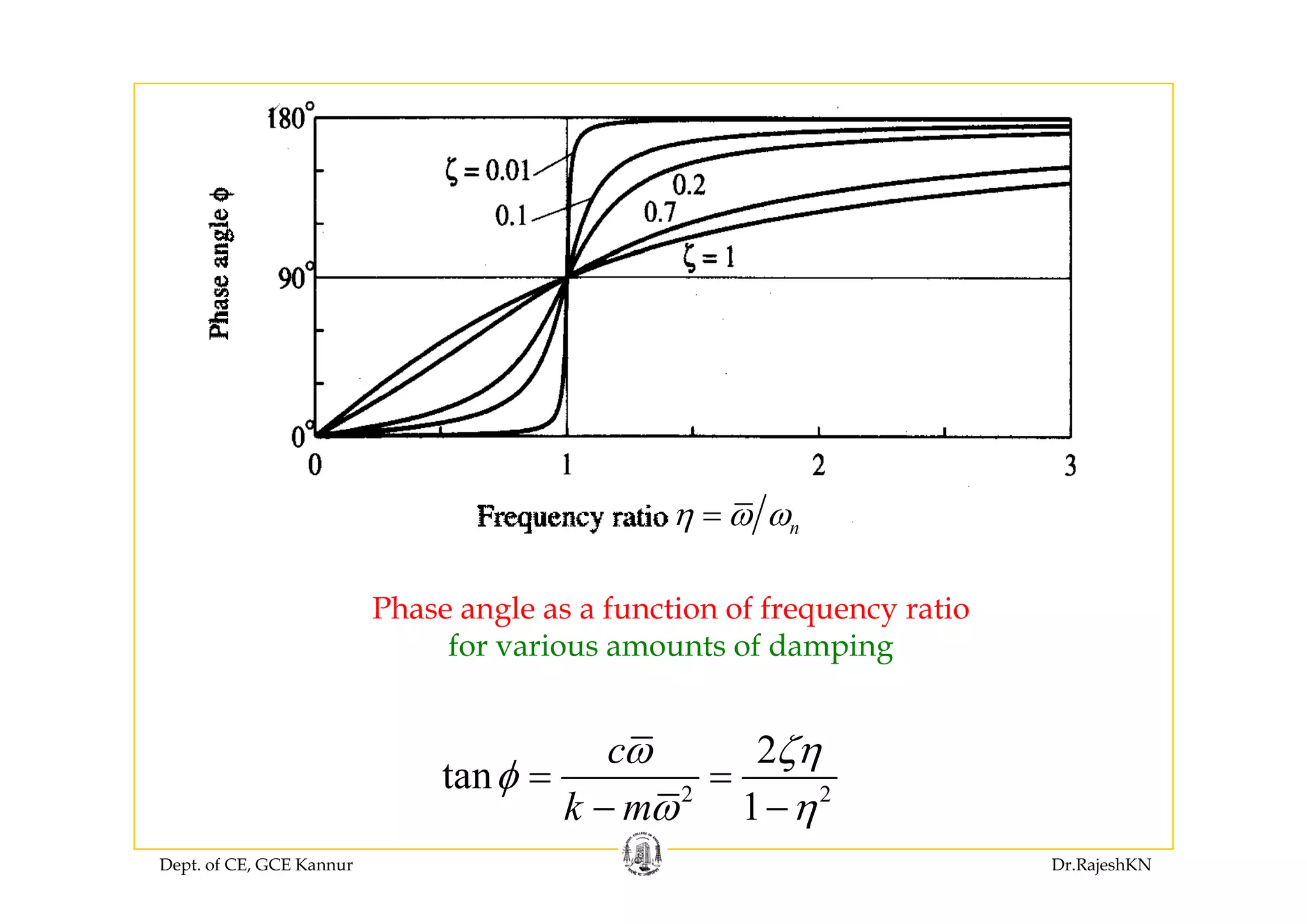
φ− 2
tan
c
k m
ω
φ
ω
=
−
( ) ( )
2 22
k m cω ω− +
cω−
( )
( ) ( )
( )0
2 22
sinp
F
y t t
k m c
ω φ
ω ω
= −
− +
Dept. of CE, GCE Kannur Dr.RajeshKN
( ) ( )](https://image.slidesharecdn.com/module4-sdynamics-rajeshsir-140806045959-phpapp02/75/Module4-s-dynamics-rajesh-sir-63-2048.jpg)

![( ) ( ) ( )( ) ( ) ( ), c py t y t y t= +Total response
[ ]
( )
( )0
cos sin sinn stt
y
e A t B t tζω
ω ω ω φ−
+ +[ ]
( )
( ) ( )
( )0
2 22
cos sin sin
1 2
n
D De A t B t tζ
ω ω ω φ
η ζη
= + + −
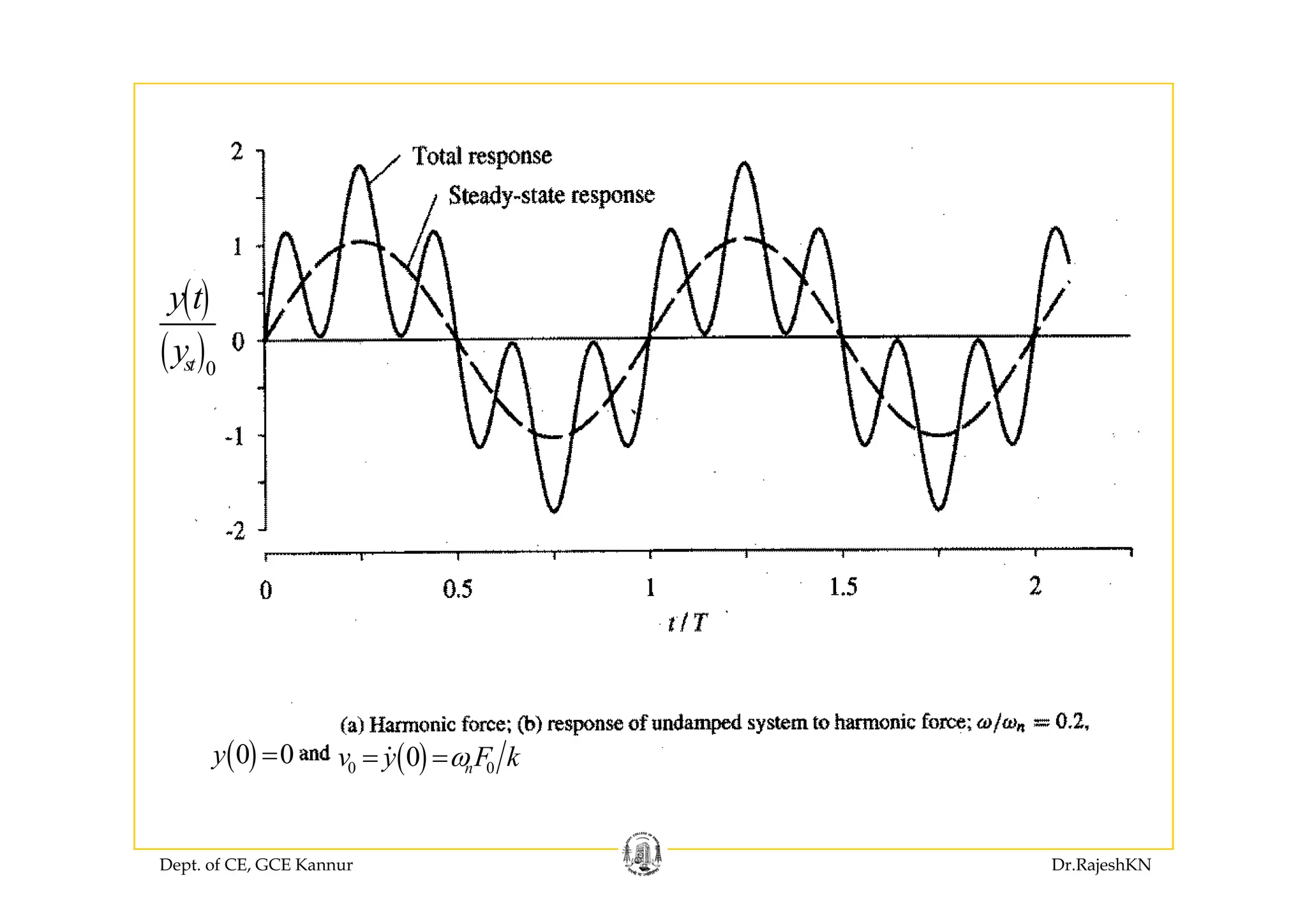
− +Transient response
Steady state response
Dept. of CE, GCE Kannur Dr.RajeshKN
65](https://image.slidesharecdn.com/module4-sdynamics-rajeshsir-140806045959-phpapp02/75/Module4-s-dynamics-rajesh-sir-65-2048.jpg)