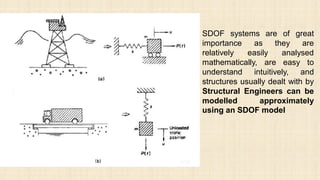
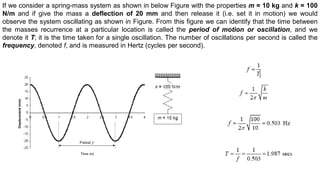
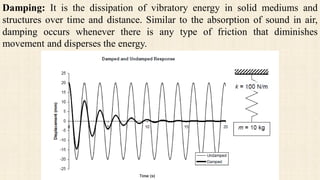
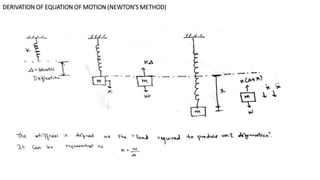
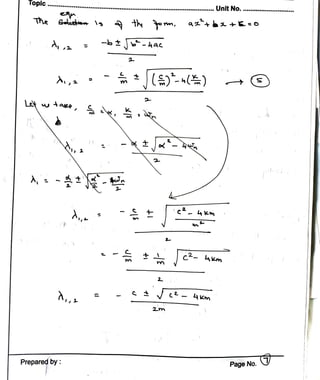
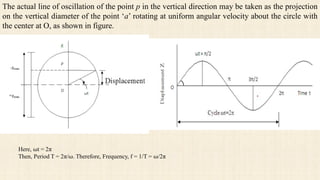
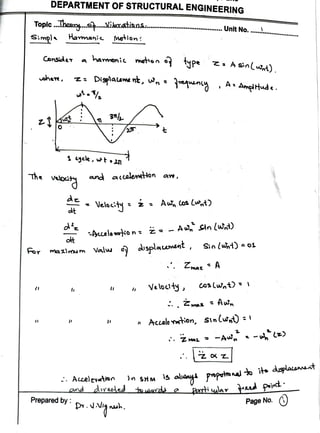
1. The document discusses the theory of vibrations as it relates to equipment foundation design. It covers topics such as simple harmonic motion, free and forced vibrations, damping, and single degree of freedom systems. 2. Foundations may experience static or dynamic loads from various sources like earthquakes, blasting, wind, and machinery which can cause the foundation and soil to vibrate. 3. Simple harmonic motion is the simplest form of periodic motion where the acceleration of a point is directly proportional to its displacement from a fixed reference point.

1. EQUIPMENT FOUNDATION DESIGN- II
Unit 1: Theory of Vibrations
By
Dr. V. Vignesh. M.E., Ph.D.
Assistant Professor,
Sanjivani College of Engineering, Kopargaon

2. UNIT 1. THEORY OF VIBRATIONS
• Foundations may be subjected to either static loads or a combination of static
and dynamic loads; the latter lead to motion in the soil and mutual dynamic
interaction of the foundation and the soil.
• The sources of dynamic forces are
1. Violent types of dynamic forces are caused by earthquakes, and by blasts
engineered by man.
2. Pile driving and landing of aircraft
3. Action of wind and running water and so on.

5. Most motions encountered in Soil Dynamics are
• Rectilinear (translational),
• Curvilinear,
• Rotational,
• Two-dimensional, or three-dimensional, or a combination of
these.
The motion may be a periodic or periodic and steady or transient,
inducing ‘vibrations’ or ‘oscillations’.

6. Simple Harmonic Motion:
The simplest form of periodic motion is called simple harmonic motion that of a
point in a straight line, such that the
Acceleration of the point α Distance of the point from a fixed reference point
This is known as a Single Degree-
of-Freedom (SDOF) system as
there is only one possible
displacement: that of the mass in
the vertical direction.

7. SDOF systems are of great
importance as they are
relatively easily analysed
mathematically, are easy to
understand intuitively, and
structures usually dealt with by
Structural Engineers can be
modelled approximately
using an SDOF model

8. If we consider a spring-mass system as shown in below Figure with the properties m = 10 kg and k = 100
N/m and if give the mass a deflection of 20 mm and then release it (i.e. set it in motion) we would
observe the system oscillating as shown in Figure. From this figure we can identify that the time between
the masses recurrence at a particular location is called the period of motion or oscillation, and we
denote it T; it is the time taken for a single oscillation. The number of oscillations per second is called the
frequency, denoted f, and is measured in Hertz (cycles per second).

9. Basic Definitions
I. Vibration (or Oscillation): It is a time-dependent, repeated motion that
may be translational or rotational.
II. Periodic motion: It is a motion that repeats itself periodically in equal time
intervals.
III. Period (T): The time in which the motion repeats itself is called the
‘Period’.
IV. Cycle: The motion completed in a period is called a ‘Cycle’.
V. Frequency (f): The number of cycles in a unit of time is known as the
‘frequency’. It is expressed in Hertz (Hz) in SI Units (cycles per second). The
period and frequency are thus inversely related, one being simply the
reciprocal of the other.
VI. Degree of Freedom: The number of independent co-ordinates required to
describe the motion of a system completely is called the ‘Degree of Freedom

10. Types of Vibrations:
(i) Free and Forced vibration:
• The vibration which persists in a structure after the force causing the motion has been removed
is known as free vibration.
• The vibration which is maintained in a structure by steady periodic force acting on thestructure
is known as forced vibration.

11. Types of Vibrations:
(ii) Linear and Non-linear vibration:
• If the basic components of a vibrating system, namely the spring, the mass and the damper
behave in a linear manner, the resulting vibrations caused are known as linear vibrations.
These are governed by linear differential equations. It follows the law of superposition.
• On the other hand, if any of the basic components of a vibratory system behave in a non-linear
manner, the resulting vibration is called non-linear vibration. In this case, the governing
differential equation is also non-linear. It does not follow the law of superposition.

12. (iii) Damped and Undamped vibrations:
• When a damper or damping element is attached to the vibratory system, the motion of the
system will be opposed by it and the energy of the system will be dissipated in friction. This
type of vibration is called damped vibration.
• On the other hand, the vibration generated by the system having no damping element is known
as undamped vibration.
(iv) Deterministic and Random vibrations:
• If the amount of excitation (force or motion) acting on a vibratory system is completely known
precisely, the resulting vibrations are called as deterministic vibrations.
• When the amount of excitation is not completely known, the resulting vibrations are known as
non-deterministic vibrations or random vibrations. Ex: Earthquake excitation.
(v) Longitudinal, Transverse and Torsional vibration:
• When the particles of the body or shaft move perpendicular to the axis of the shaft, the
vibrations created are known as transverse vibrations.
• If the mass of the vibratory system moves up and down parallel to the axis of the shaft, the
vibrations created known as longitudinal vibrations.
• If the shaft gets alternately twisted and untwisted on account of vibratory motion of the
suspended disc, such vibrations are called torsional vibrations.

13. Damping: It is the dissipation of vibratory energy in solid mediums and
structures over time and distance. Similar to the absorption of sound in air,
damping occurs whenever there is any type of friction that diminishes
movement and disperses the energy.

14. Types of Damping:
1. Viscous damping
2. Coulomb damping
3. Structural damping
4. Active or Negative damping
5. Passive damping
Viscous damping: When the system is made to vibrate in a surrounding viscous medium that is
under the control of highly viscous fluid, the damping is called viscous damping. Viscosity is the
property fluid by virtue of which it offers resistance to the motion of one layer over the adjacent
layer.
Coulomb damping: It is a type of constant mechanical damping in which energy is absorbed
through sliding friction. The friction developed by the relative motion of the two surfaces that
slide against each other is a source of energy dissipation.
Structural damping: It is due to the internal molecular friction of the material and also due to
the loss of energy associated with the slippage of structural connections. Resulting damping forces
oppose the motion, and hence the amplitude of the response that is displacement is decreased.

15. Types of Damping:
Active or Negative damping: Active damping refers to energy dissipation from the system by
external means, such as controlled actuators, etc. In this damping, the amplitude tends to increase
which lead to instability of the system. This type of supplying energy to the system is known as
negative damping.
Examples: Suspension bridges, transmission line wires.
Passive damping: It refers to energy dissipation within the structure by damping devices such as
isolator, by structural joints and supports or by structural member's internal element.

16. Simple Harmonic Motion:-
Let us assume a mass ‘M’ or ‘W’ suspended by a spring having stiffness of ‘k’ with no damping,
as shown in Figure

17. The actual line of oscillation of the point p in the vertical direction may be taken as the projection
on the vertical diameter of the point ‘a’ rotating at uniform angular velocity about the circle with
the center at O, as shown in figure.
Here, ⍵t = 2π
Then, Period T = 2π/⍵. Therefore, Frequency, f = 1/T = ⍵/2π

18. The equation of motion is represented by a sine function
X = A Sin(⍵nt)
where, X = Displacement
ωn= Frequency in radians per unit time (angular velocity)
A = Amplitude
The velocity and acceleration are
Velocity= dx/dt = A⍵nCos(⍵nt)
Acceleration = d2x/dt = -A⍵𝑛
2 Sin(⍵nt)
For maximum displacement, Sin(⍵nt) = 1
Therefore, Xmax= A
For maximum velocity, Cos(⍵nt) = 1
Therefore, X’max= A⍵n
For maximum acceleration, Sin(⍵nt) = 1
Therefore, X′′max= −A⍵𝑛
2

19. Free Vibration without Damping

20. DERIVATION OF EQUATION OF MOTION (NEWTON’S METHOD)

22. • A vertical cable 3m long has a cross sectional area of 4cm2 supports a weight of
50kN. What will be the natural period and natural frequency of the system? Take
E=2.1x106 kg/cm2.
• A one kg mass is suspended by a spring having a stiffness of 1N/mm. Determine
the natural frequency and static deflection of the spring.

24. Forced Vibration without damping:
If a mass supported by a spring is subjected to an exciting force, the system undergoes forced
vibrations. Such an exciting force may be caused by unbalanced rotating machinery or by other
means.
The exciting force is periodic and it may be expressed as
F=Fo Sin ⍵t
Where, Fo is the max. value of exciting force.
⍵ is the circular frequency of exciting force.
The equation of motion for the system may be written as,

26. Refer Written Notes

27. Free Vibration with Damping:
Let us assume that in a system undergoing free vibrations, a damping is added as shown in figure,
The governing equation of motion is written as,

29. Refer Written Notes

30. DEPARTMENT OF STRUCTURAL ENGINEERING
Topic..heang.s..xatian...
Simpla Hamonie motion:
for
Consder
shere,
kwt
the vo
1 eycle, wt 21
dt
a hamonie motion type
3n
Prepared by :
and acealenton ane,
Velscity e 2 A, cos lwnt)
ot
mazimu m Volw
Valw dsplanent
-Aeceleion |:-A sAnlwt)
Acelevtion
pr.gm
Veloeity
Jn sH M IS
Unit No. ...
Ze Asin(wn)
Accelention, SinC
. Z mal
AAmpltude.
Sio(w) 01
- )
aliday ppotnal it dgplaanet
patti ulaY
Page No. )

31. Fzamgle A harmonic
T=
12
A HM
N
|2 -
has
Max Aceelerion e Aw,
Delermne
6mls
Un
Aeo.& Cm.
man
has a m
Time perted . T'a
Man. Ae
n Ts. 348 ad/
Mac-Velocity Aw,
RPDINA ADARGAN
21
Wn
3}42.Yodls
Maa-Velbcy ma s and
2
344. 89
6 A(1s. 598)
and
79. 6 mm.
O4X342
12 LPS.
aLelerlon.
)s.
4s2,sIl, mm/st.
an
ampltitucets pernd and its maraLc.
ampltud

32. Topic ....Dadamt...$A.Näazi.a.2RE....Unt No.....
Respose q SpoF ytem
The
i) Equivaln spoF ytem
a) The ineytta
<) he
qatton
Prepared by:
+he
FREE VigeARION
a) the exctg ora,
b) the estort ng ore (oo spnng or 52 kx
k
F
m
most importat to detemine thh dy ham'e beharto,
mi t c tk* Ft.
gnh
m
motion
F4)
F
F4).
ONDAMpED Sof SYSTEMmi
K
SDoF sytem
Page No.

33. The duovmatton
The tonstont
Auoding to
the eon
b writen a
Deivotion
Proportonal
in which
A-static
Fs= kx.
Degletian
arety progotonal to the tore, e.,
Pmporhonalty
Kno
The en o motton
the atis
Can loe
neton's
mation
o mton hch stoe tha
Equtoy
to th
drned
Seond a
batwn he
auts
spag contant on stu spng k
Seh
a
mgrses
is jut another om
tore and dsplaet oa
ka
F ma
KA
undanpud gree vibotion ytem
Mstton. ( Netons method)
the vate chang
Nuton's Seond lsw
momentm is
o and tales plae
in the dreeton
to prode unit dmtion

34. Topic...
Some
eguslborum positon
Retong toru in
Prepared by:
pru nd then
then the
e
X dreHon
knoe tht
to Neten's law,
m >
pbgorg is Yeoved.
wiko
Unit No. ...
W- K(A)
KA- Ko -Ks
m
PageNo.
S.

35. EJanple:3
n
A mass t
a
6oo m:The mass
ditan
a) Equatton moion
b Natuval
a) Total
meHon:
Saipended bya spmng kang a sjns
dsplated dousno d mts uilbrm pasition by
)The n pense o the systom
Çind
<) Ces ponse the ystem:
Totad en&
the
the
the sgt
x. ASinlwnt)
3 398 Hz.
X: O-coISin (24y 49t)
quncton o
mazlmwn
Kinetic ener,
my
o.03 o.o3
tine.
potntd anangy
2

36. Example:s A
A one
Determine
state
mass
Aqletson
2T
2
A
we kow tht ke
m
(000
mA
and stacte dqdon the sprtg
3 q.xom 9.8 mm.

37. Topic
FoRCED VBRATIO
ezhg tora
mass
by the means.
the exatimg
The
*Ghg teree, the System wndegou oras ibratisng. Suh
where, Fo is he
Sna
Prepared by:
NTHOUT DAnpIN
m
tawen
Supported
.
F" F, sinwt
Grculr
be
tore is penodie
ma x Vaus
as
Cawede
m FoSinwt
>
motion
m t koc Fo Sin wt
m
m
he
Sin wt
Snat
nit No. .....
ng has mon'e.
Unit No.
Sjectel to
wnbalaned otating athnag
bt eopruid au
in Yad sec
applie ore is hanmonie he mtin d the syten
be orithen a,
Page No. 4

38. Suwst
Tt
thu
Can
Ast
app licatton
A
the
any pott time
t olows that t eguany o a orced vibracon
rod o
-w ASin wt
F
be euriten a,
where
tore.
to
Pezledton
)
mwn
A
the
Fo
Sinát
tho
Ast
Fo
Sin wt
K
mwli-)
called the ryy
Vibradhon is eal
the gsten wndor Fo 'aplied stadicay
K
dusplaemenprodud
is aied the 'maggehon tcso
to
statc dsplaomert.
lay stadi

39. Topic
i) when
in diete that
that
)
Same
oth the ezuton
that
oth
total Response.
pl
th
hen B , e w>wthe
are
drecton. the dsplaamerd
the
enutdion. Ths Caweg
anplituda
Sasd to be
dynamie displatamant and
dynamis dyplaemt
Prepared by :
< wn
L is the most
Thw resonan
to be Yeonat. This
ENGINEERING
ohoh mamum aplituo
the Ma s
tton
is
when therey aqied loadg
Unit No. ....
be
becos
cbserel,
phenomenen
Oturs.
.positive. This
the wndampud natulrguny Systeas, the syen
wl be
n magh is innte ushieh indcteu
Savd to be in
in phele
negtive.This indicades
posite to he dieson
Said to be oud Aphae
Ibeating pheno mannin the
importan Concep in Shncural dynami.
is Cailed Rosonace.
orong guany at
Page No.

40. ViBRATON S
Assungthat
s presunt a sha
From FGD the
Let
chore
m
the
tuso toots.
wItH DAmpini
aove
the
Swost thw
n
Cotta
m
Valuw n
m
dRenhal ton
to o Atemnad.
Knon
m F)20
FB9.
Ket
mtion anloe wren
et
charactenetie ewton wheh ha

41. Topic
the
Let wtaee,
Prepared by:
,,
th
-bt-
4ac
*(-()
sle
2,
2m
2
Unit No.
Page No.

42. Thes
tollouing
Case :
1s tered
The roadical
Cose 24
Jstat comupondng
Comapond
a r
Esvdton
when the
damg
duscrimihant
Y
overdampd
ndurdamped ystem. th ots
damped
the
mston
dsemnad
Pret
to simple eqondkay daan
for
Aisunmi had
in
2
Ce
Ce
dis cernmen term nqn )
the
m
2
charatertte euaion fasd
is
The
postve (greten than Zen), th ystem
uoton
m
eots
are
ejual to ze th
orth
loecomes
Culed
2.mun
motlon.
Conpltx candgatu,
an puly al on
tem stermet
moton:
the
Teo, te stewal Whe
2mwn
ytem

43. SANJIVANI COLLEGE OF
KOPARGAON
Topic
For
The rio
Zeo
Let
An Autonomous Institute AFfIliated to SPPU, PUne
DEPARTMENT OF STRUCTURAL
ENGINEERING
Sanjivani Rural Education Society's
a crtcal
whenee
Prepared by :
OFENGINEERING,
daled
tis most iporart Paamr
means
are th os
tend
dmeiones quantty
A,t
e
ctheaty
to
t disumlnate
tothected dapi
2m
UnltNo..........
'n
the euten,
LA+
J4is dented y a
LA+aJ
daig
mwd be
Thw
Page No.
to