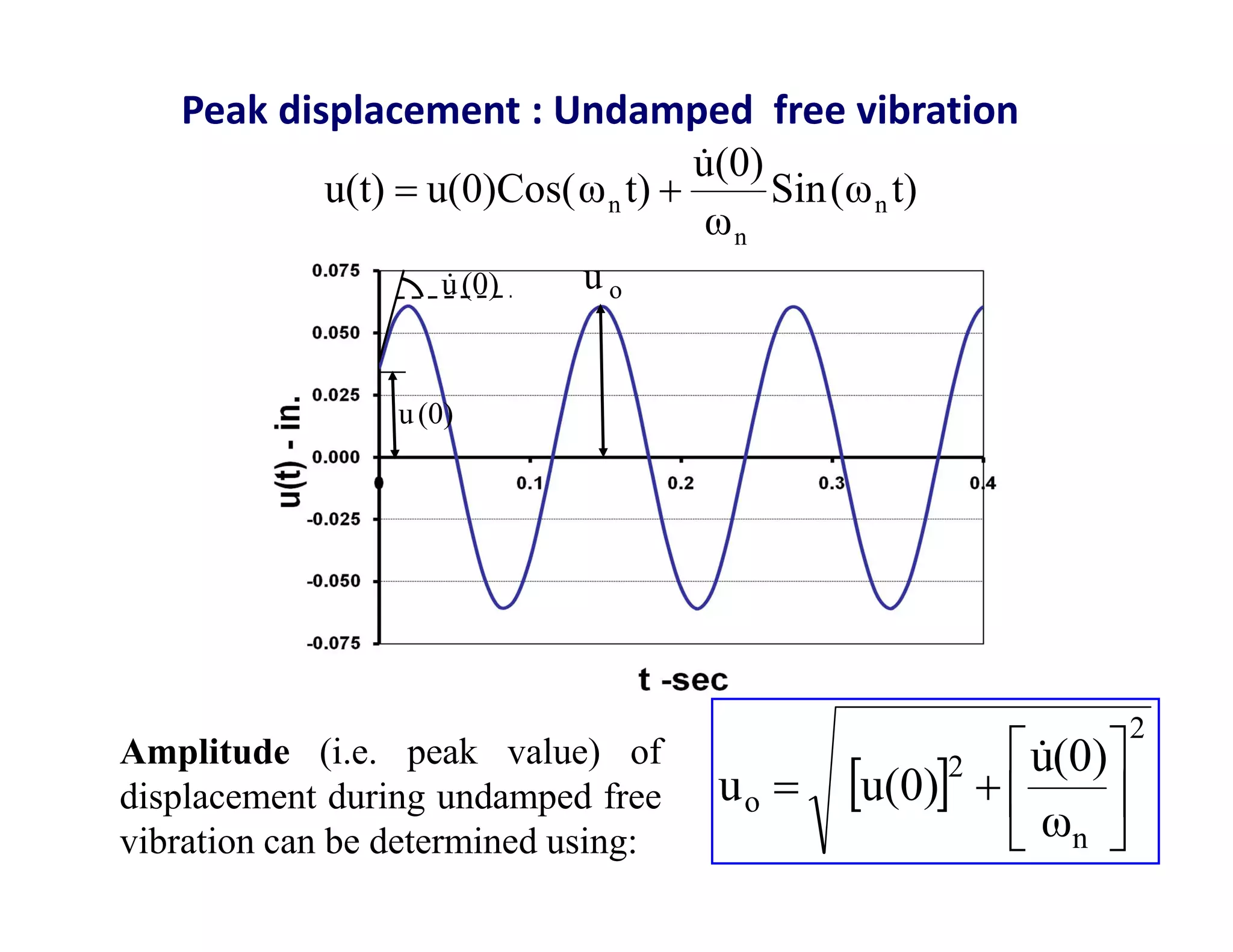
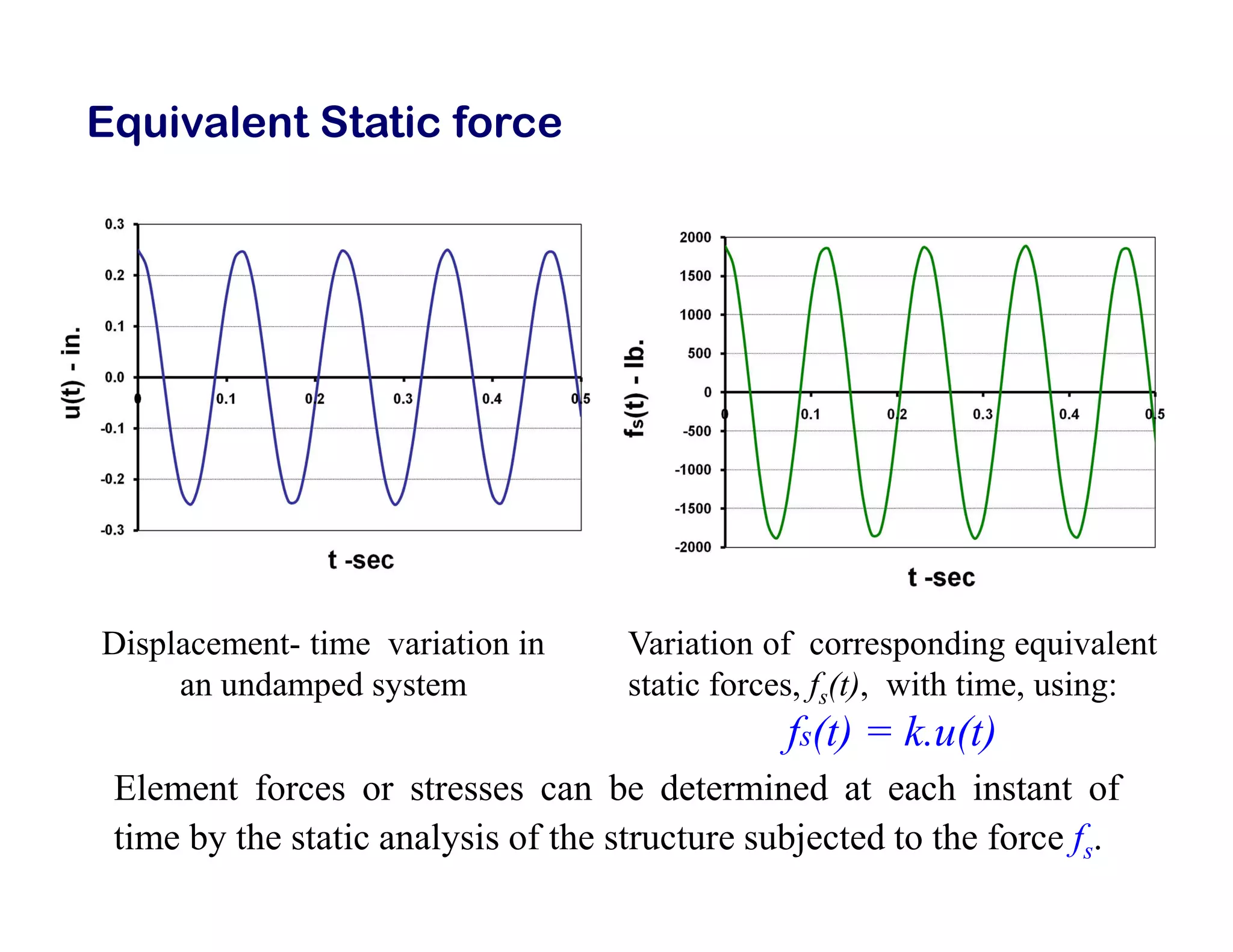
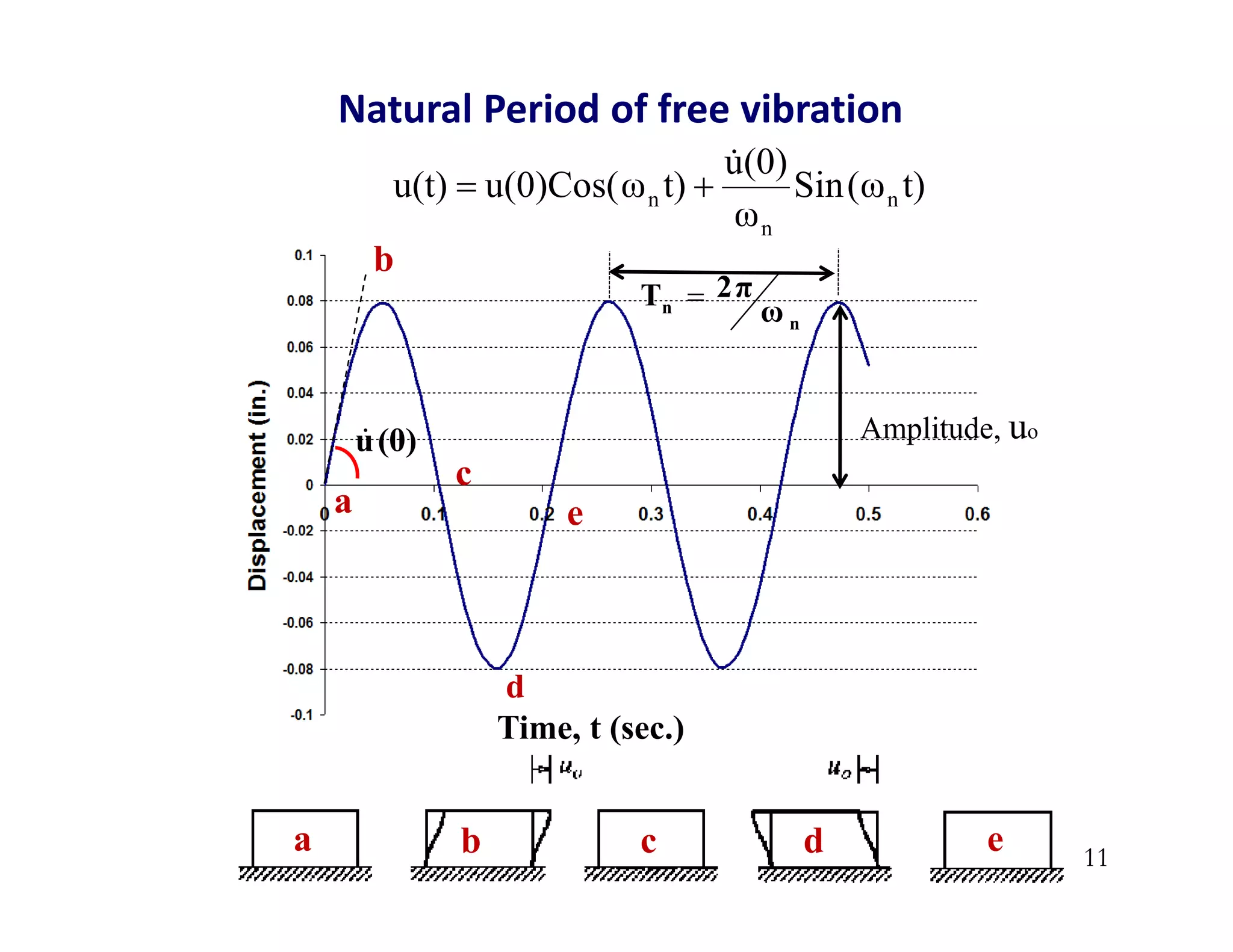
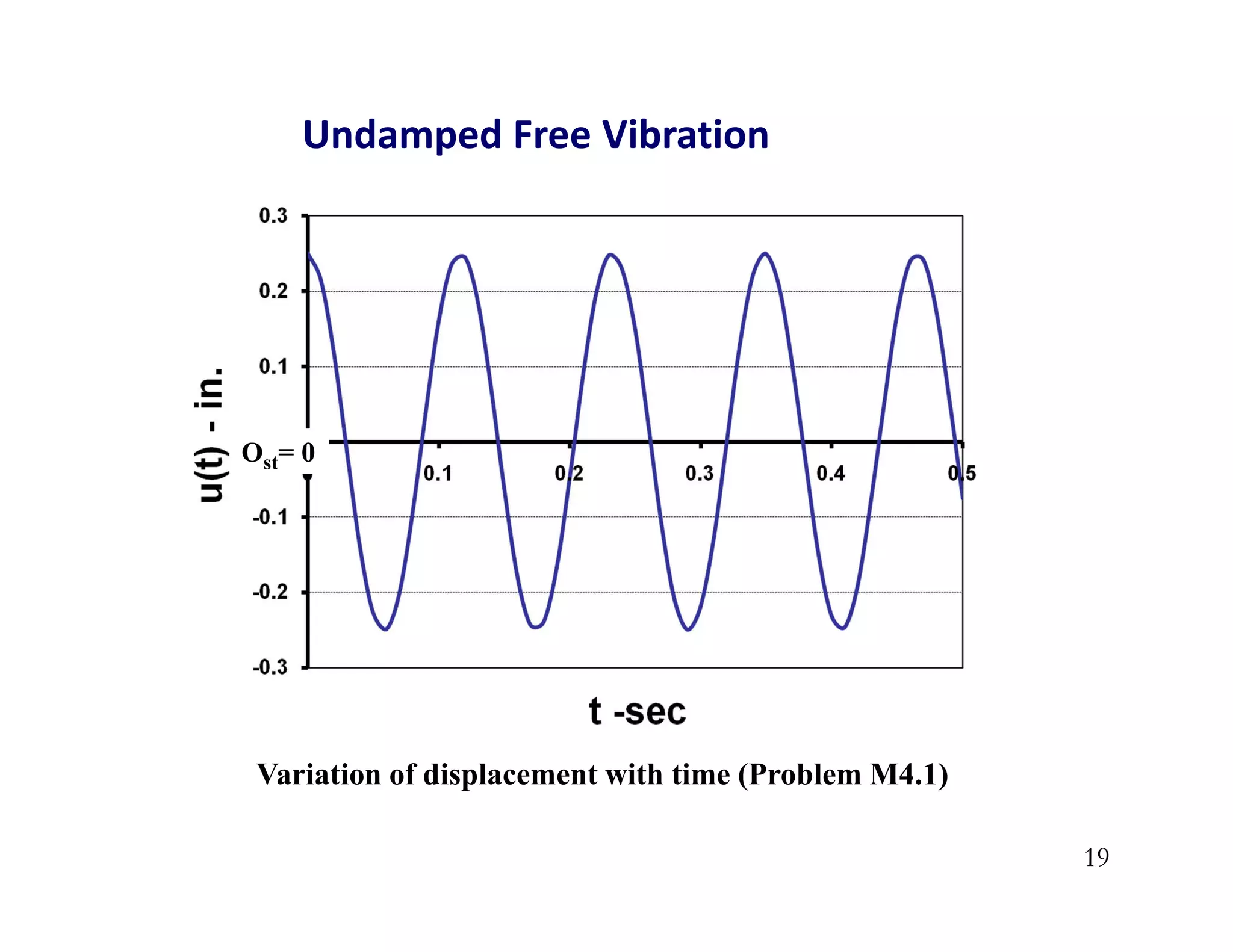
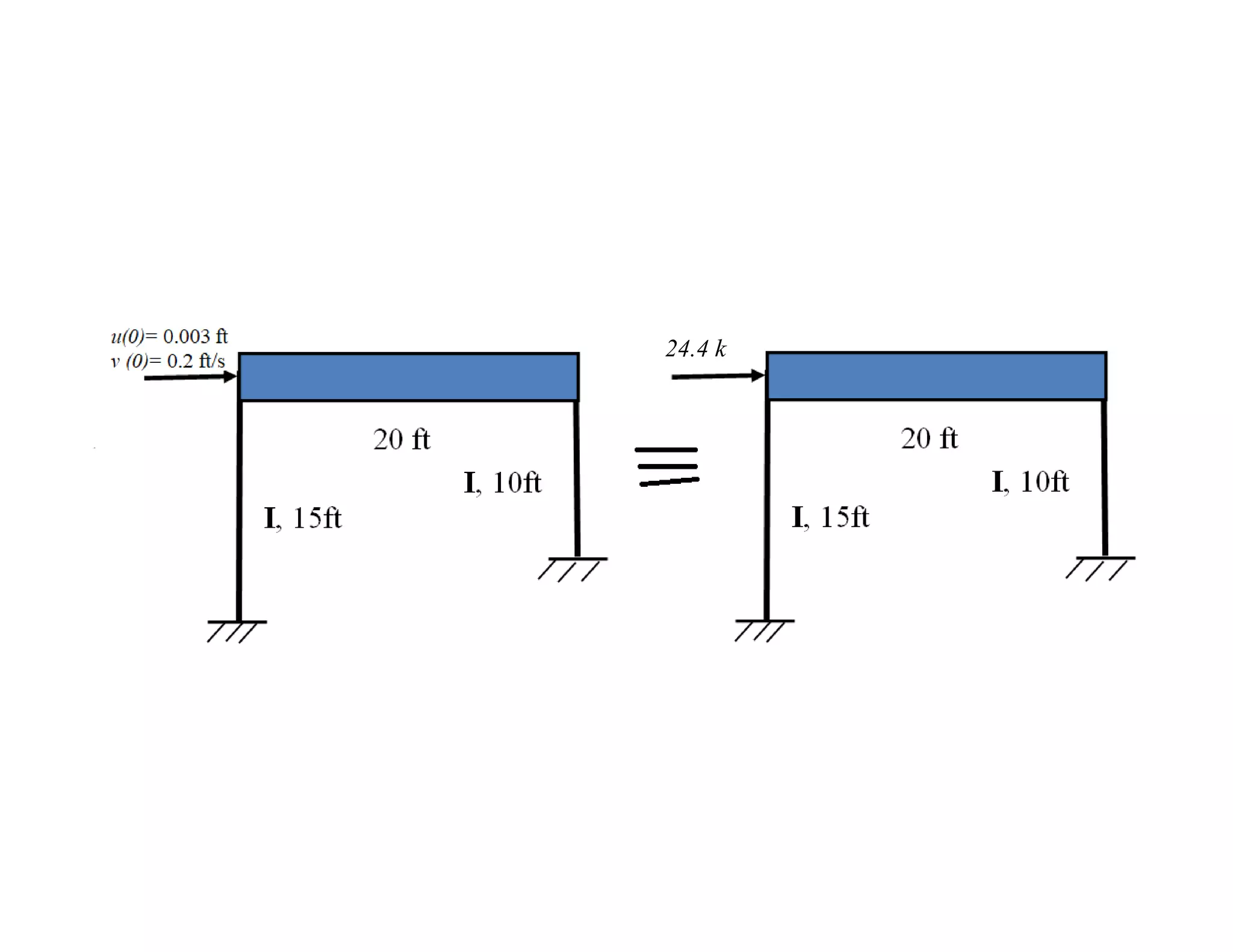
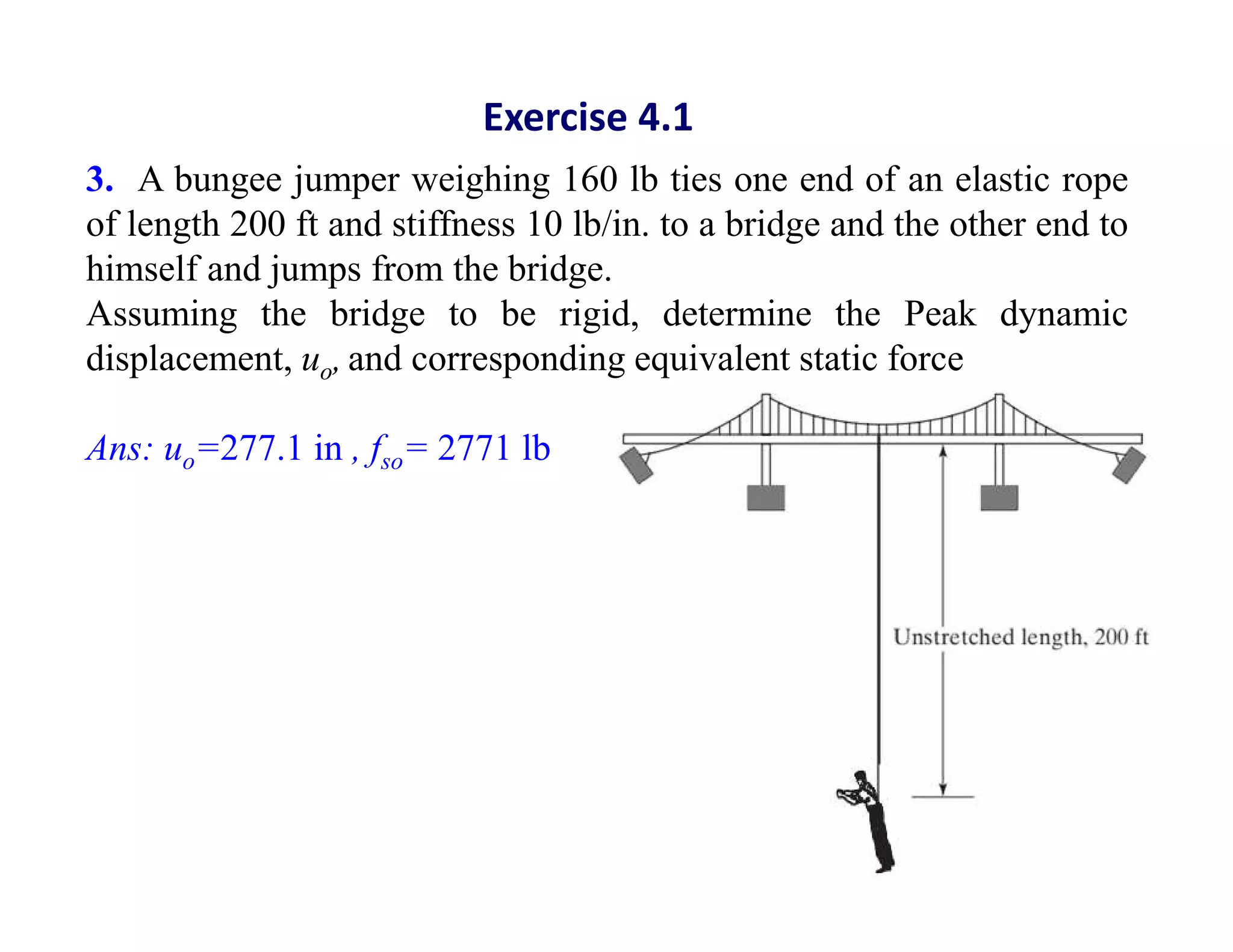
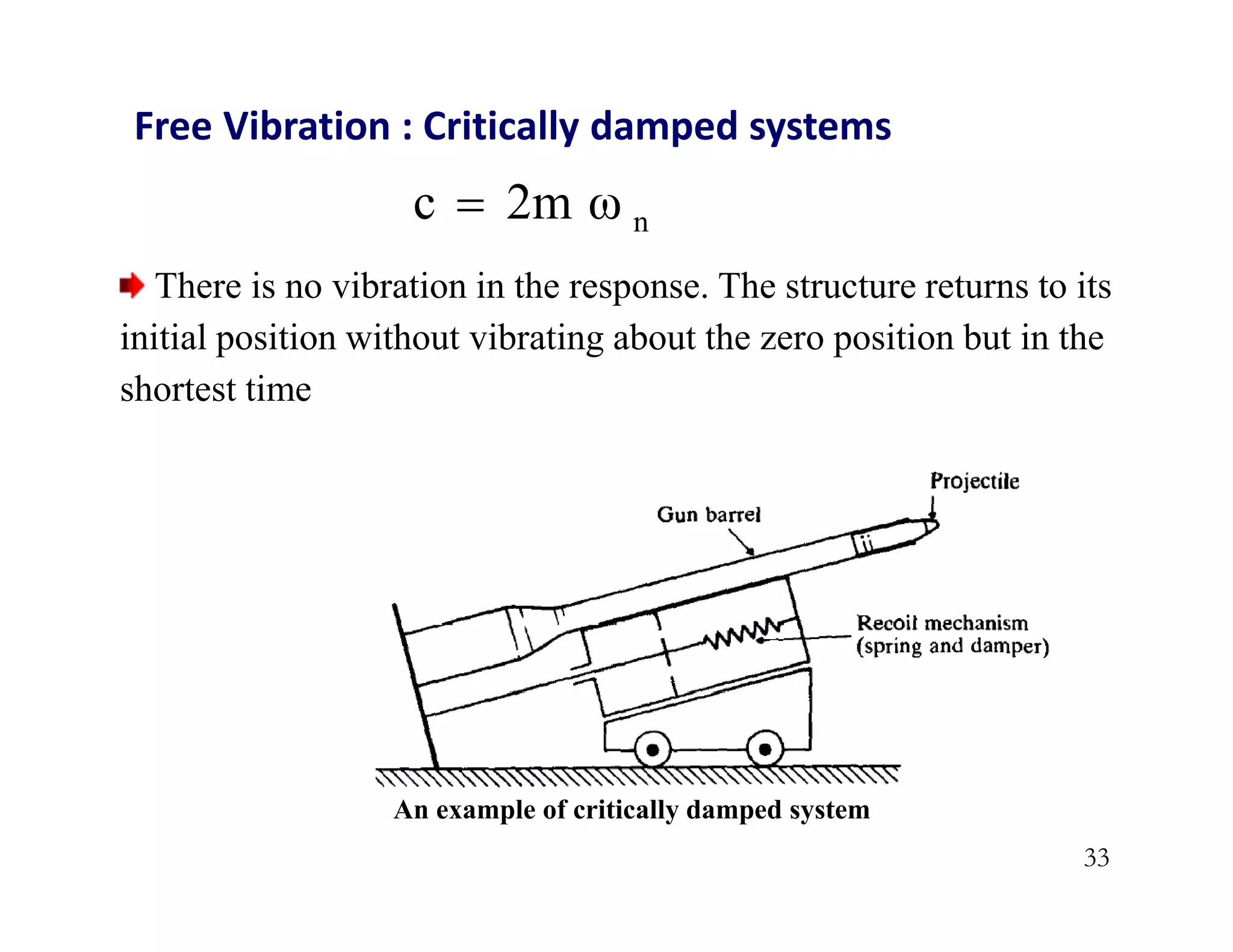
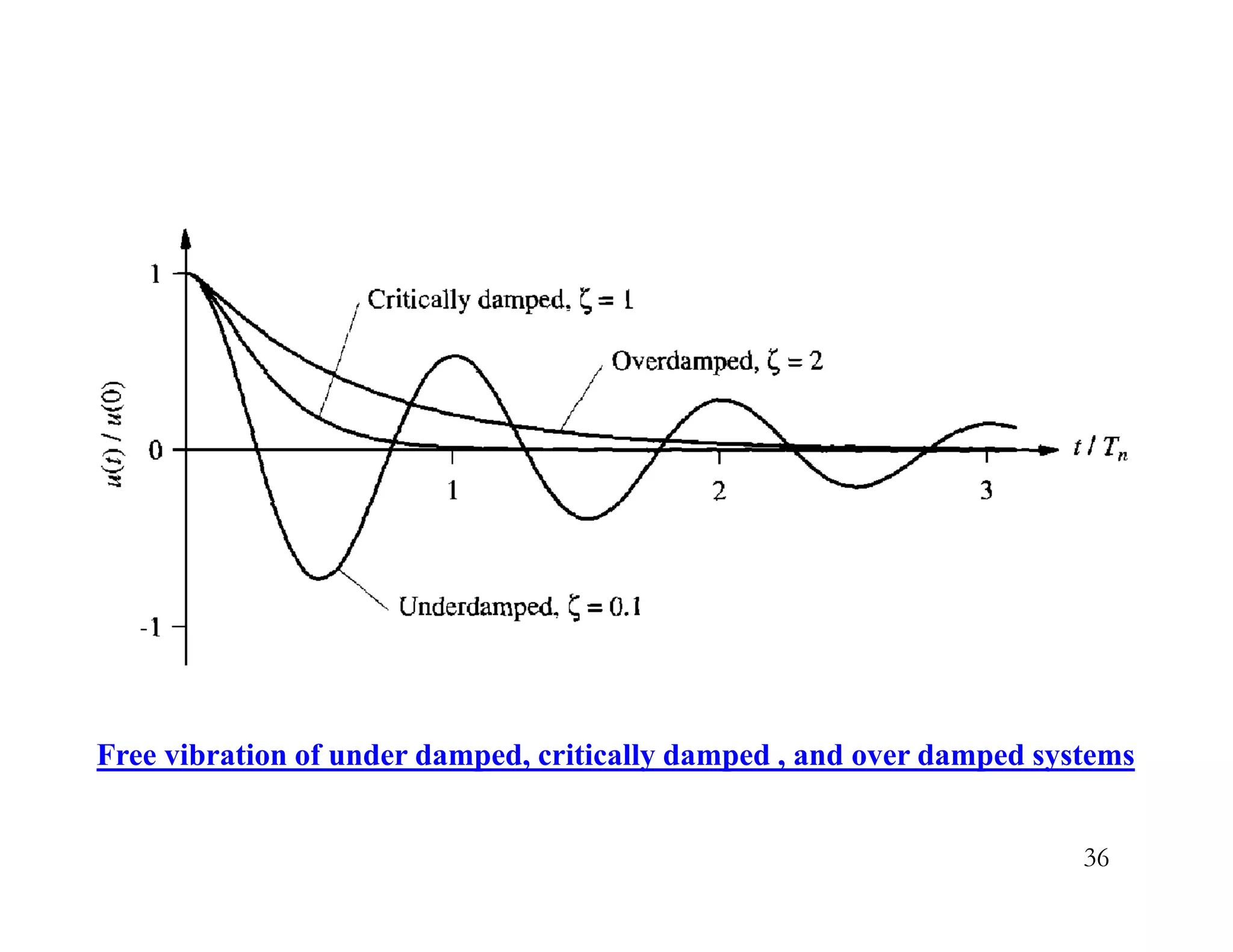
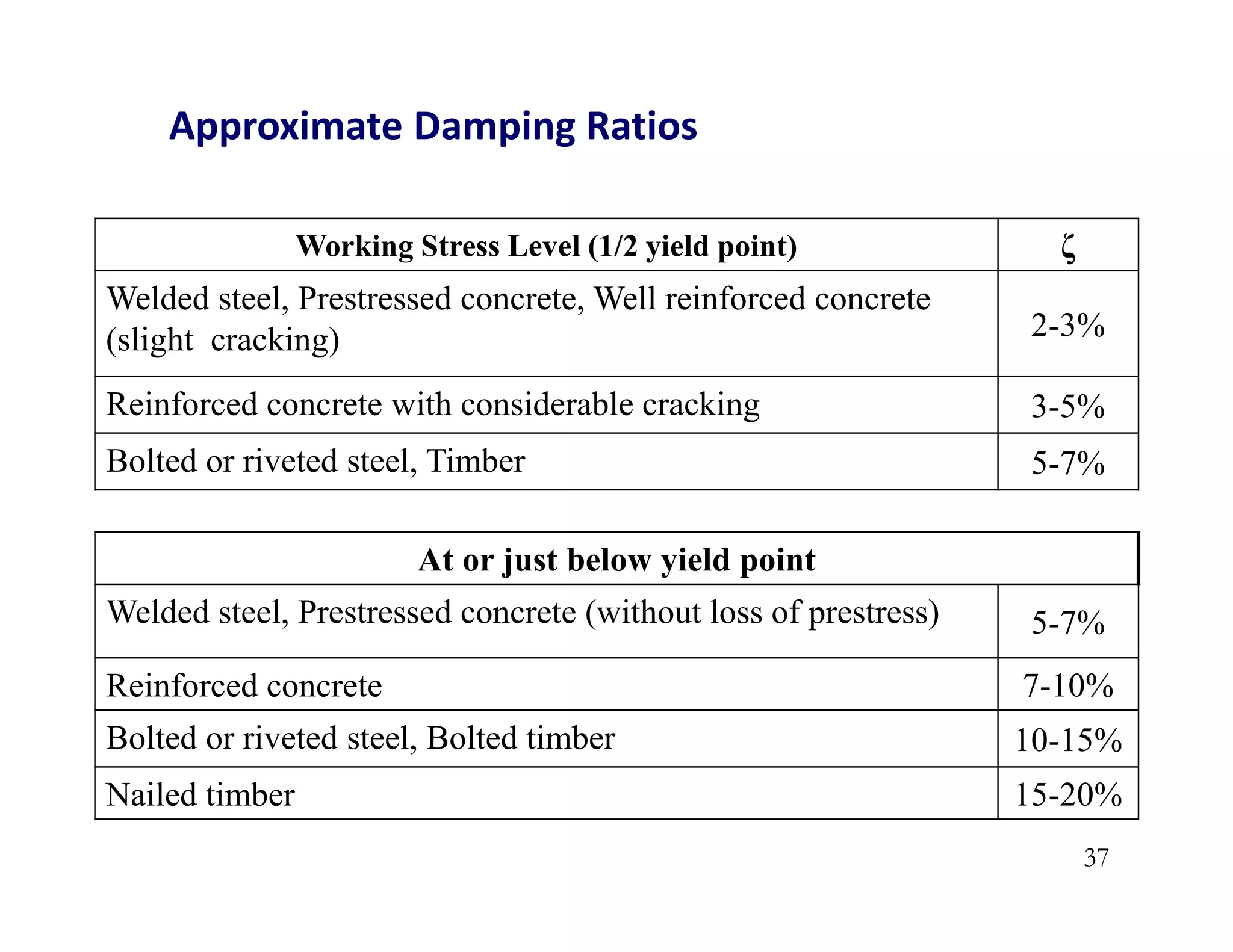
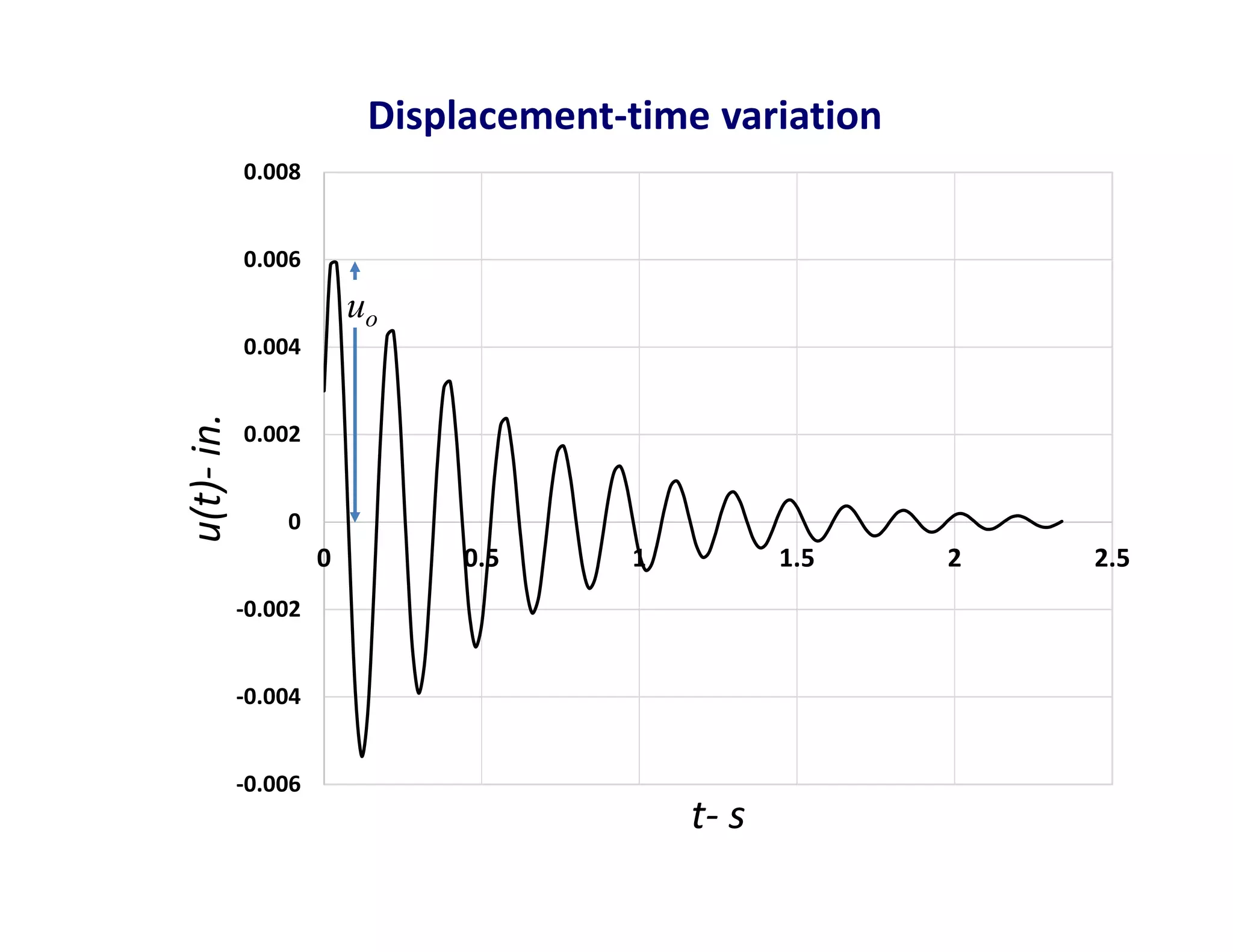
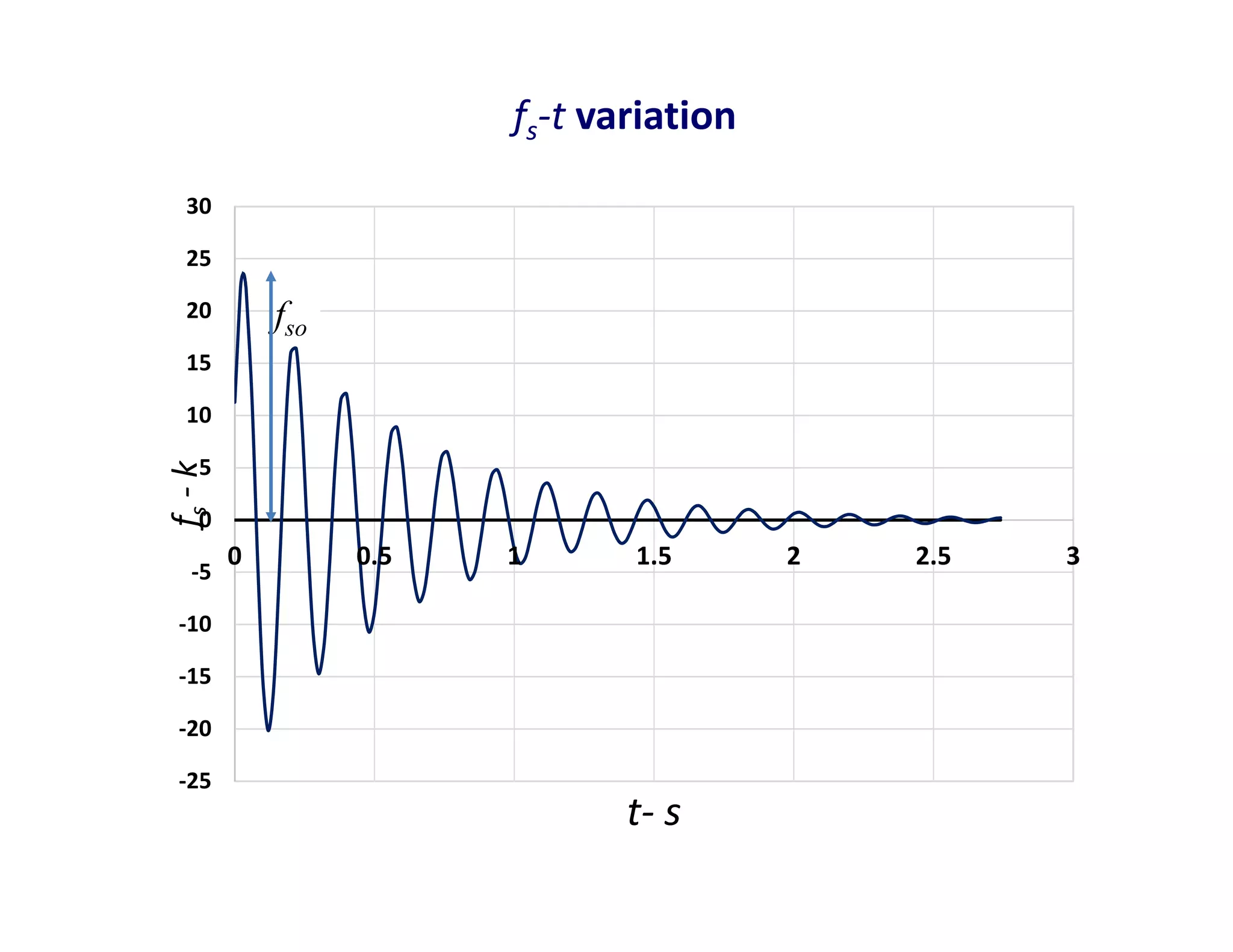
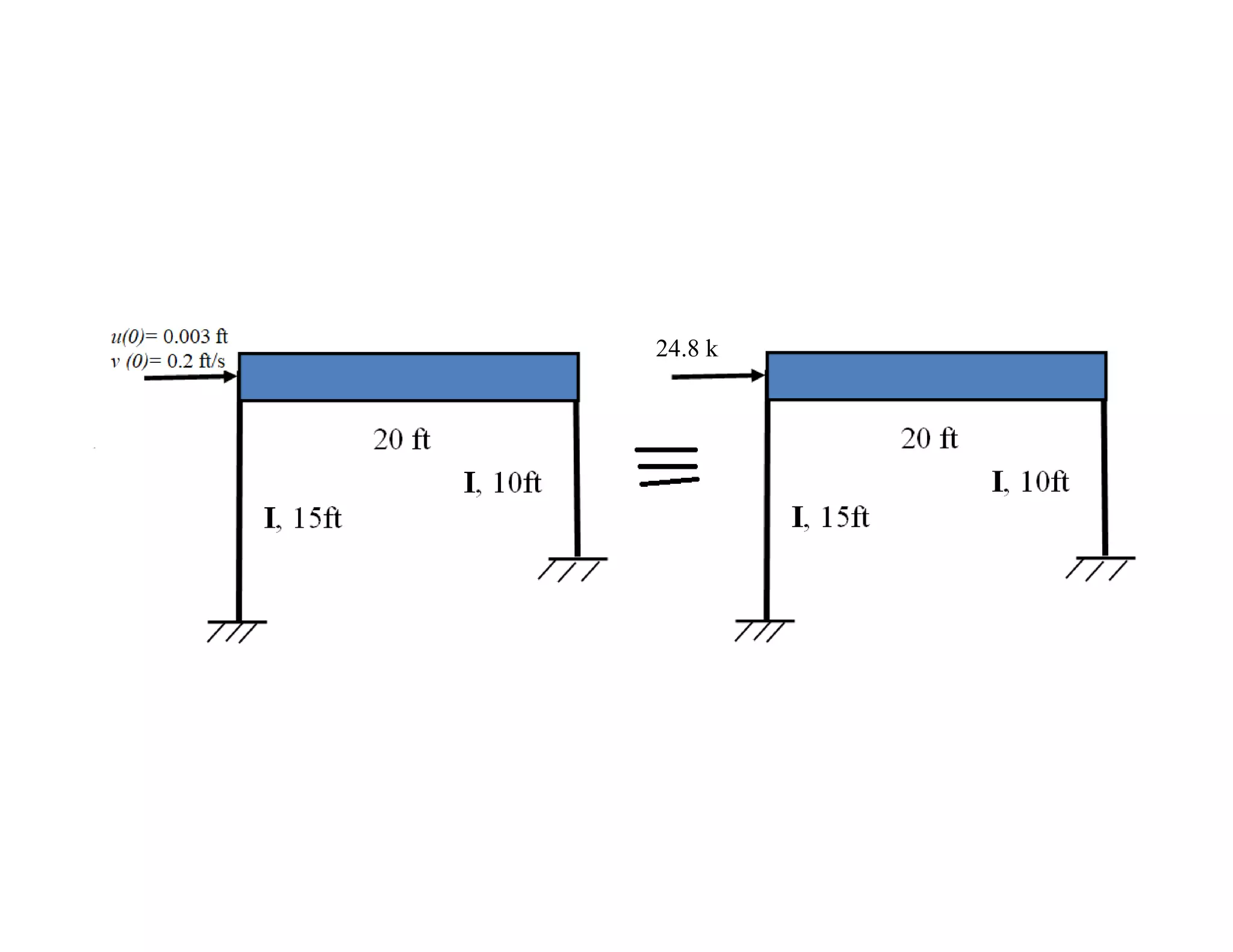
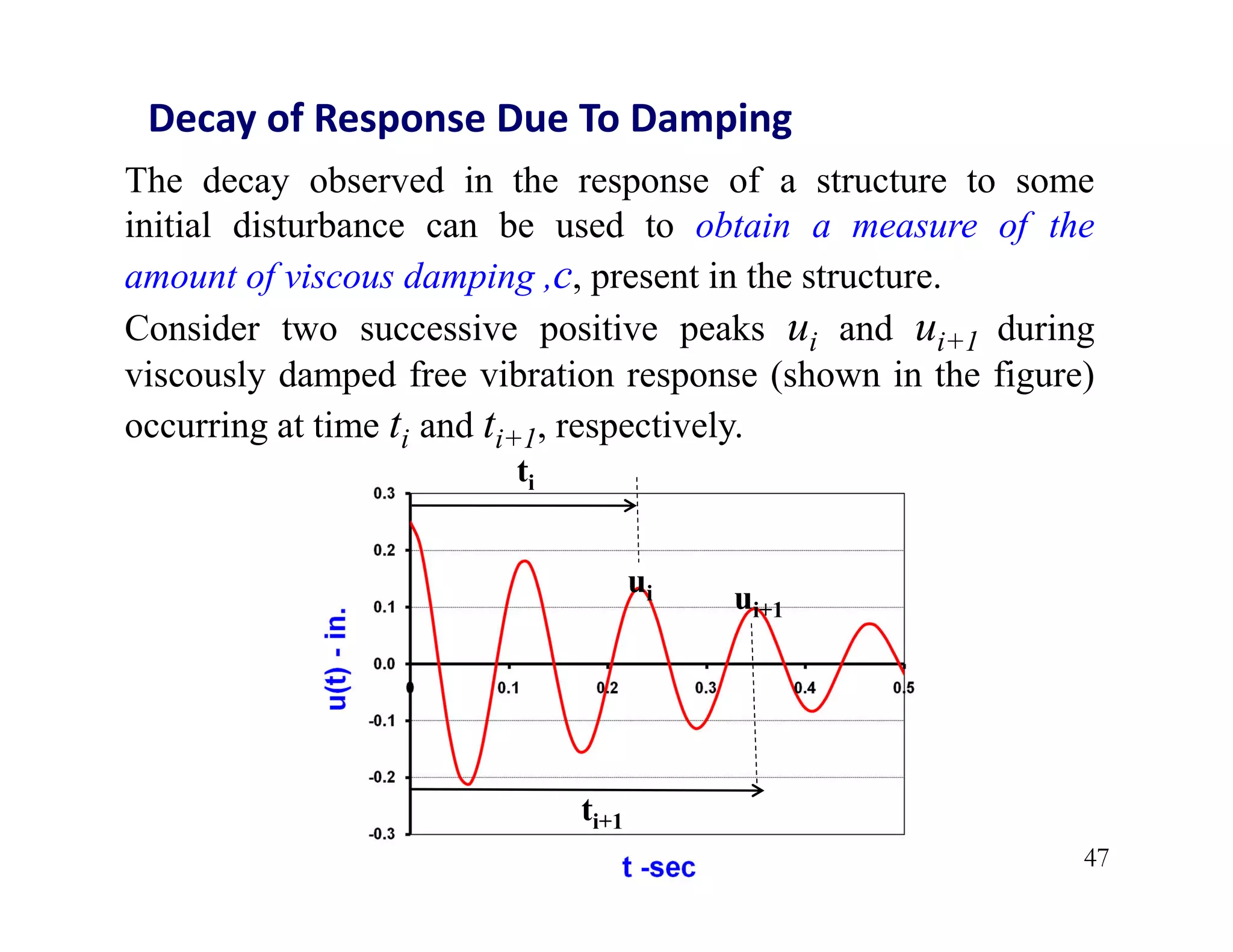
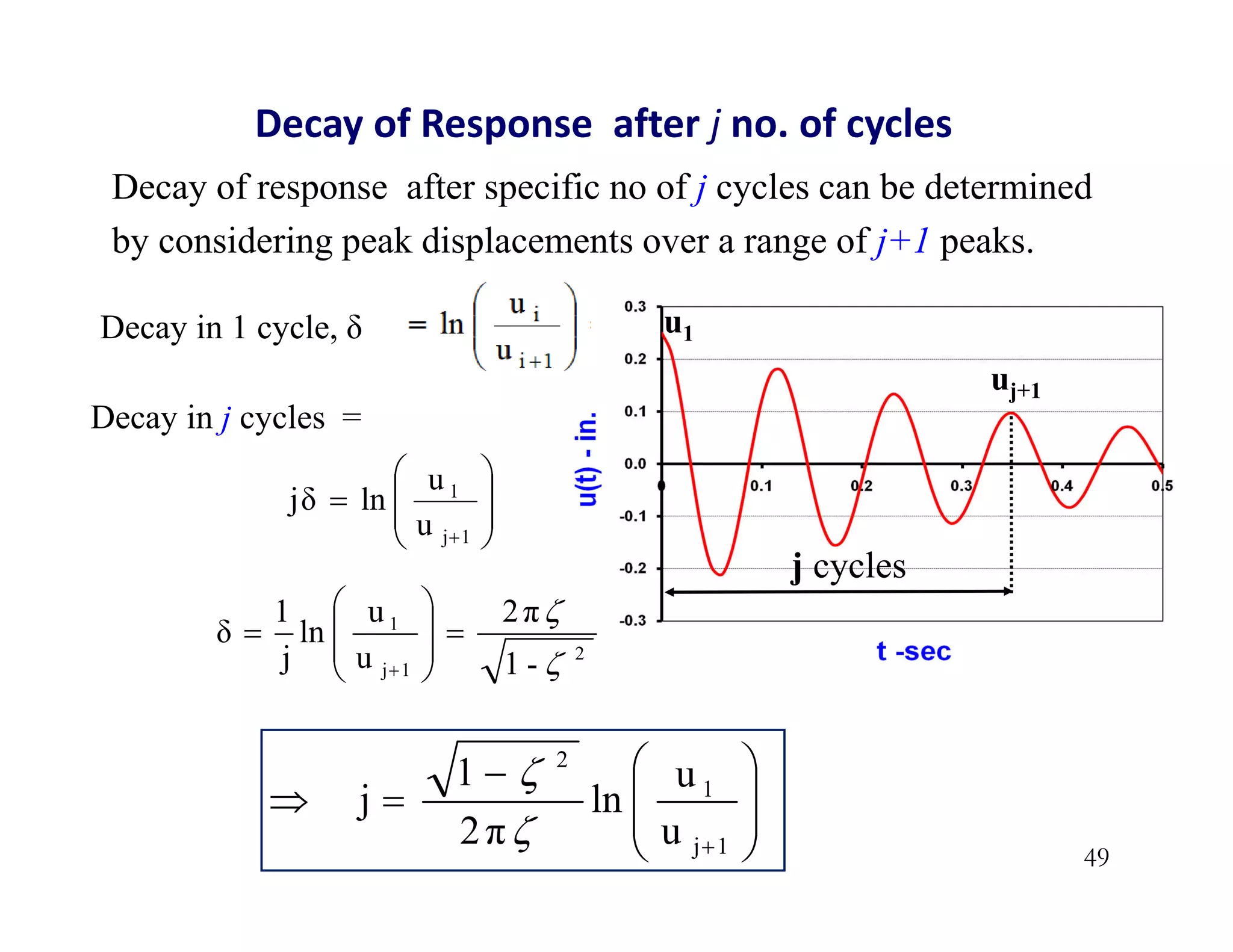
The document discusses the response of single degree of freedom (SDOF) systems to undamped and damped free vibration. It provides the equations of motion and solutions for undamped free vibration. It discusses the effects of initial conditions and how to determine the natural frequency, period and equivalent static force. The document also discusses viscously damped systems and provides solutions for underdamped, critically damped and overdamped systems. It provides typical damping ratios for different structural materials and systems. Example problems are also included.