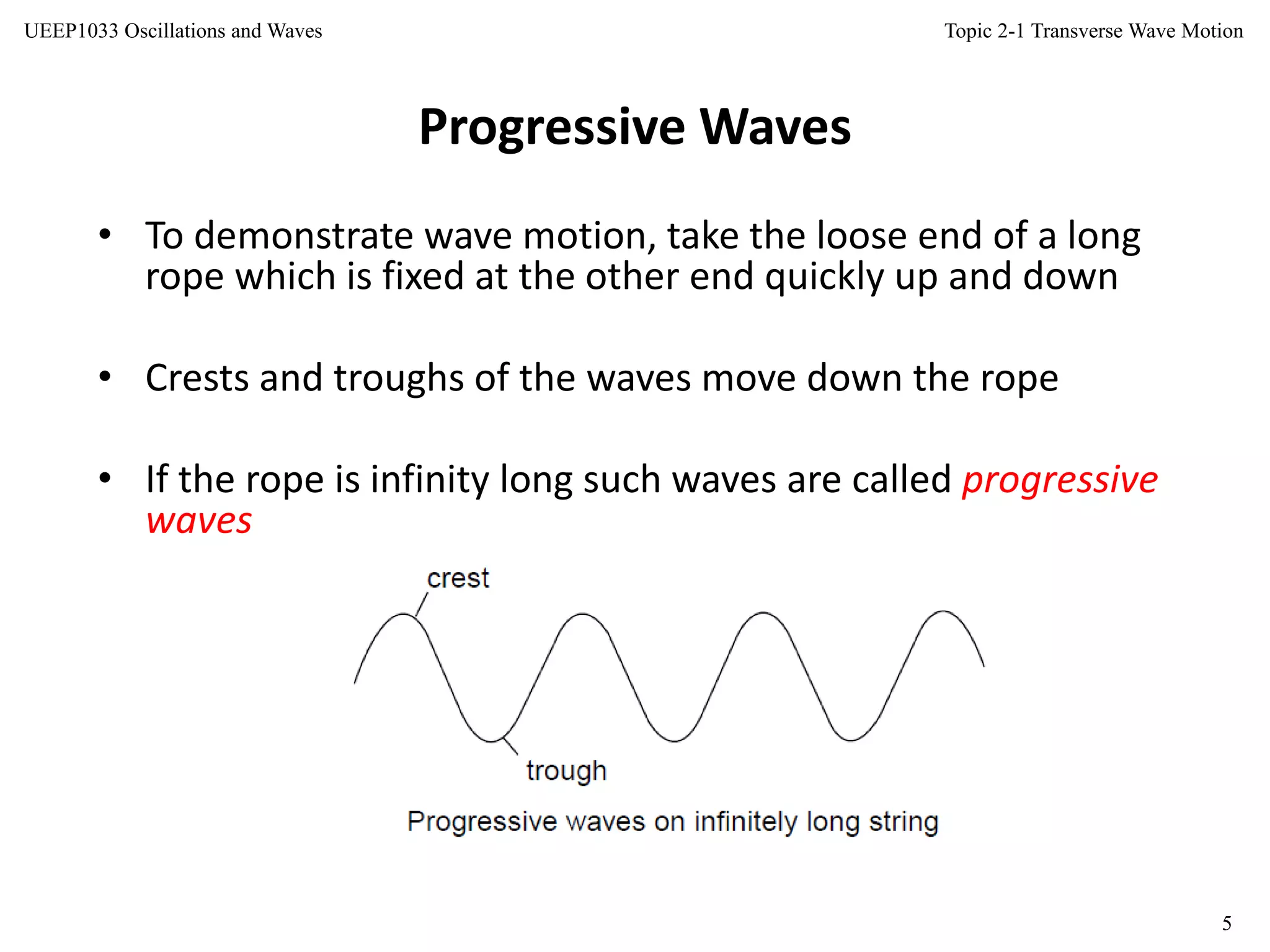
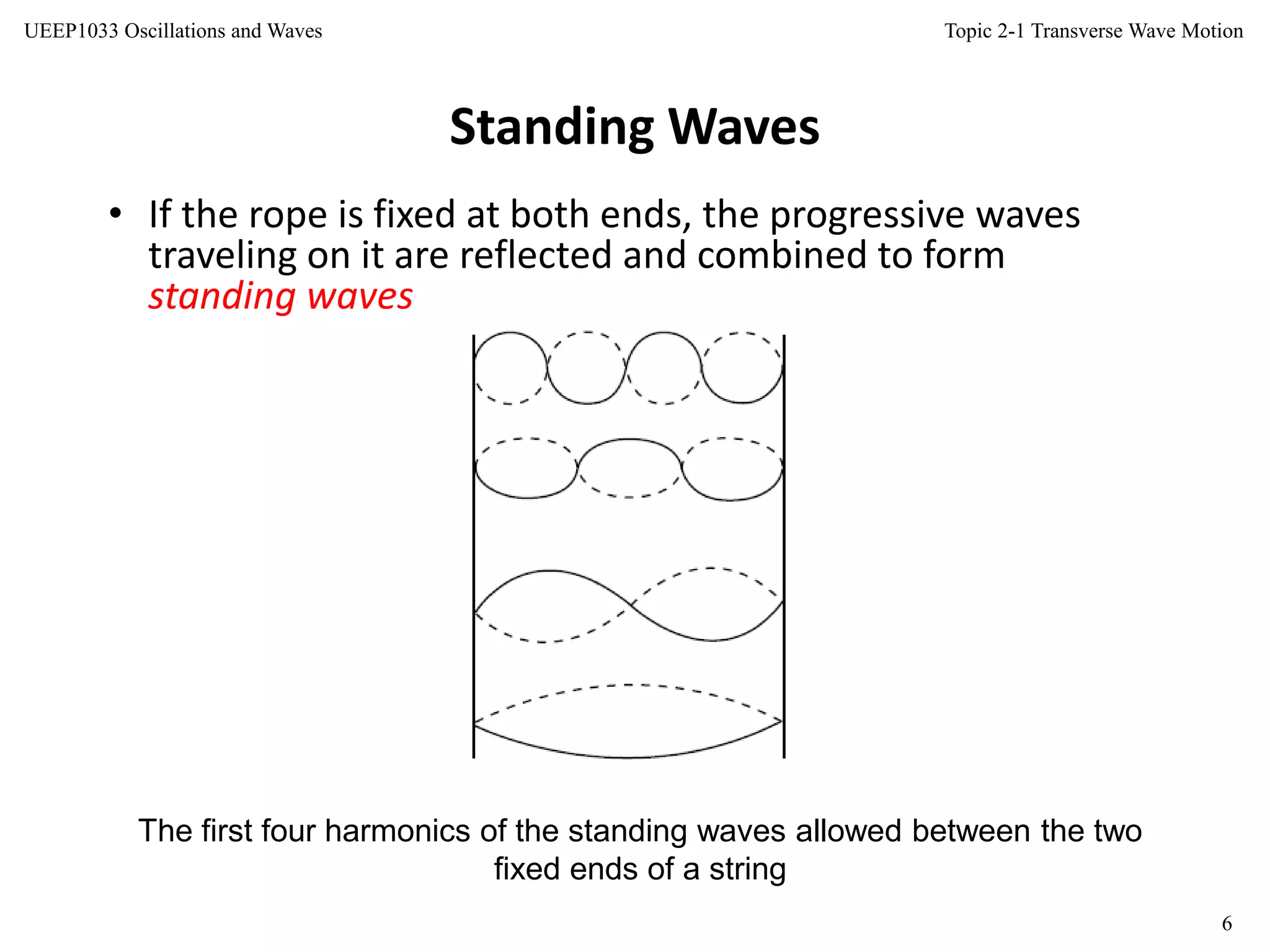
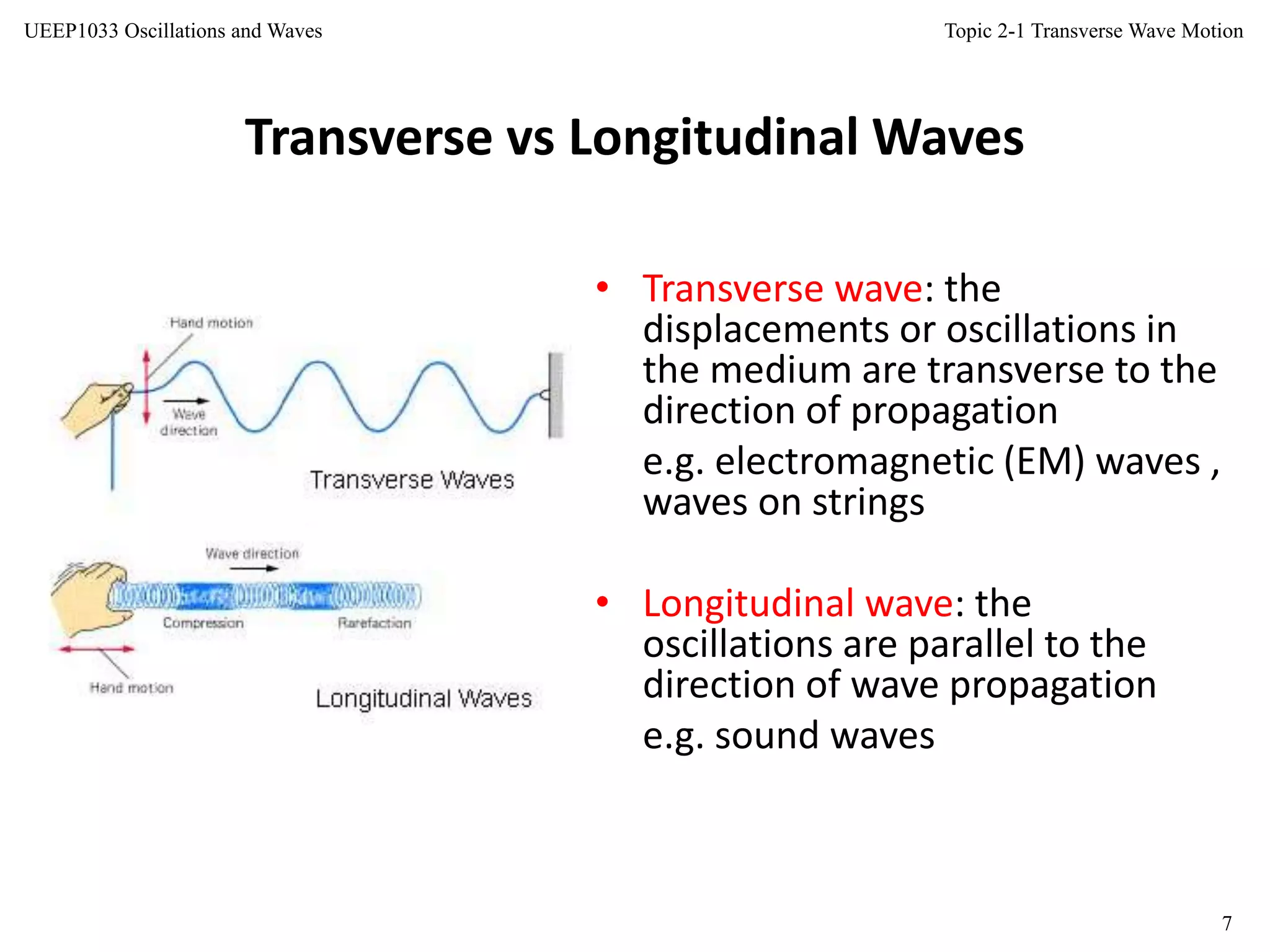
This document discusses transverse wave motion. It defines transverse waves as disturbances that occur perpendicular to the direction of propagation. Transverse waves include electromagnetic waves and waves on strings. The document covers characteristics of waves like wavelength and frequency. It derives the one-dimensional wave equation and explores solutions and properties of transverse waves, including phase velocity, group velocity, and impedance. Key concepts covered are the definitions of progressive and standing waves, and the distinction between particle/oscillator velocity and wave/phase velocity.






































































![Topic 2-1 Transverse Wave Motion
84
UEEP1033 Oscillations and Waves
The expansion of the above equation is known as a Fourier
series and the amplitudes A1, A2, . . . as Fourier coefficients or
Fourier amplitude
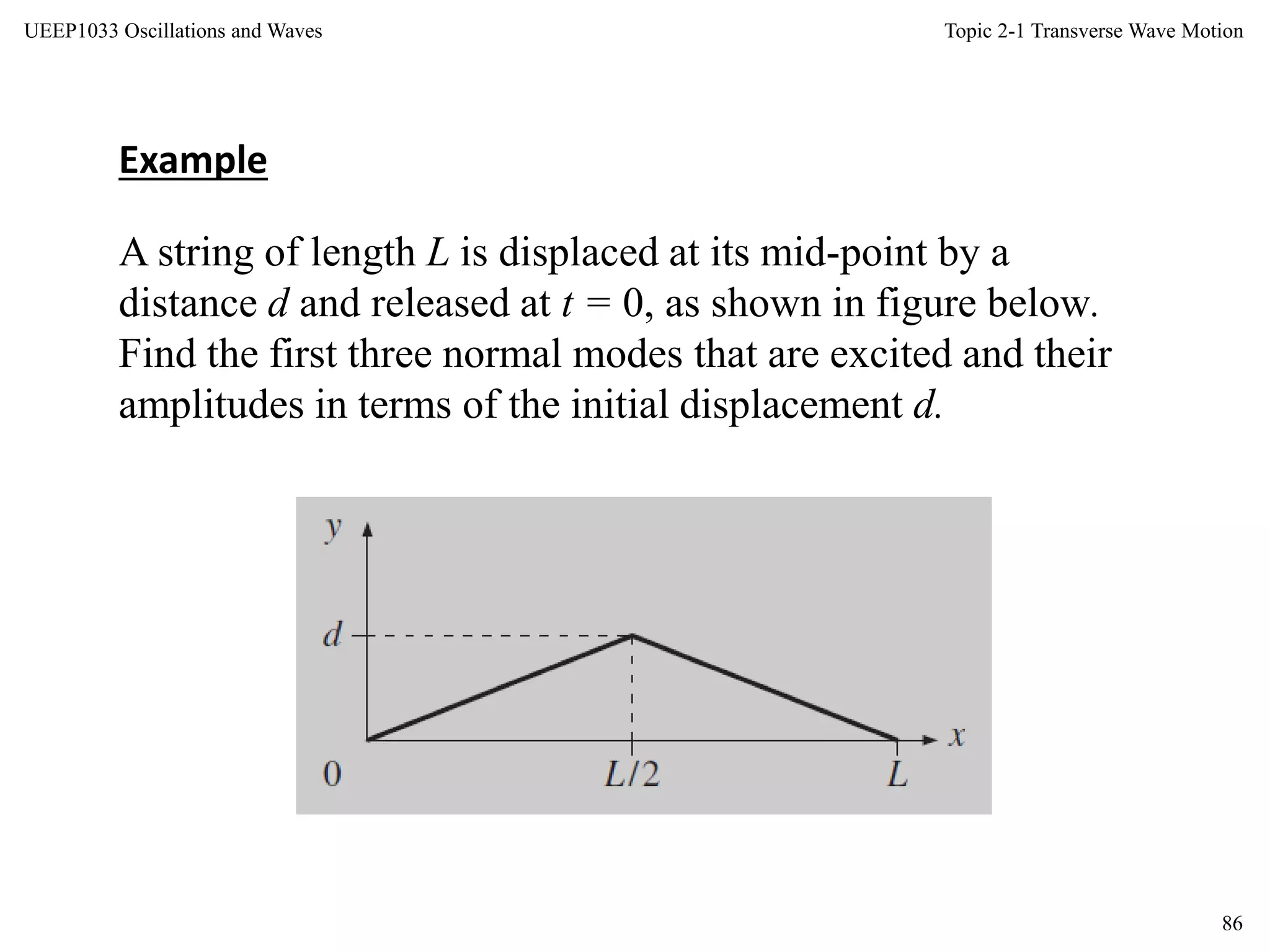
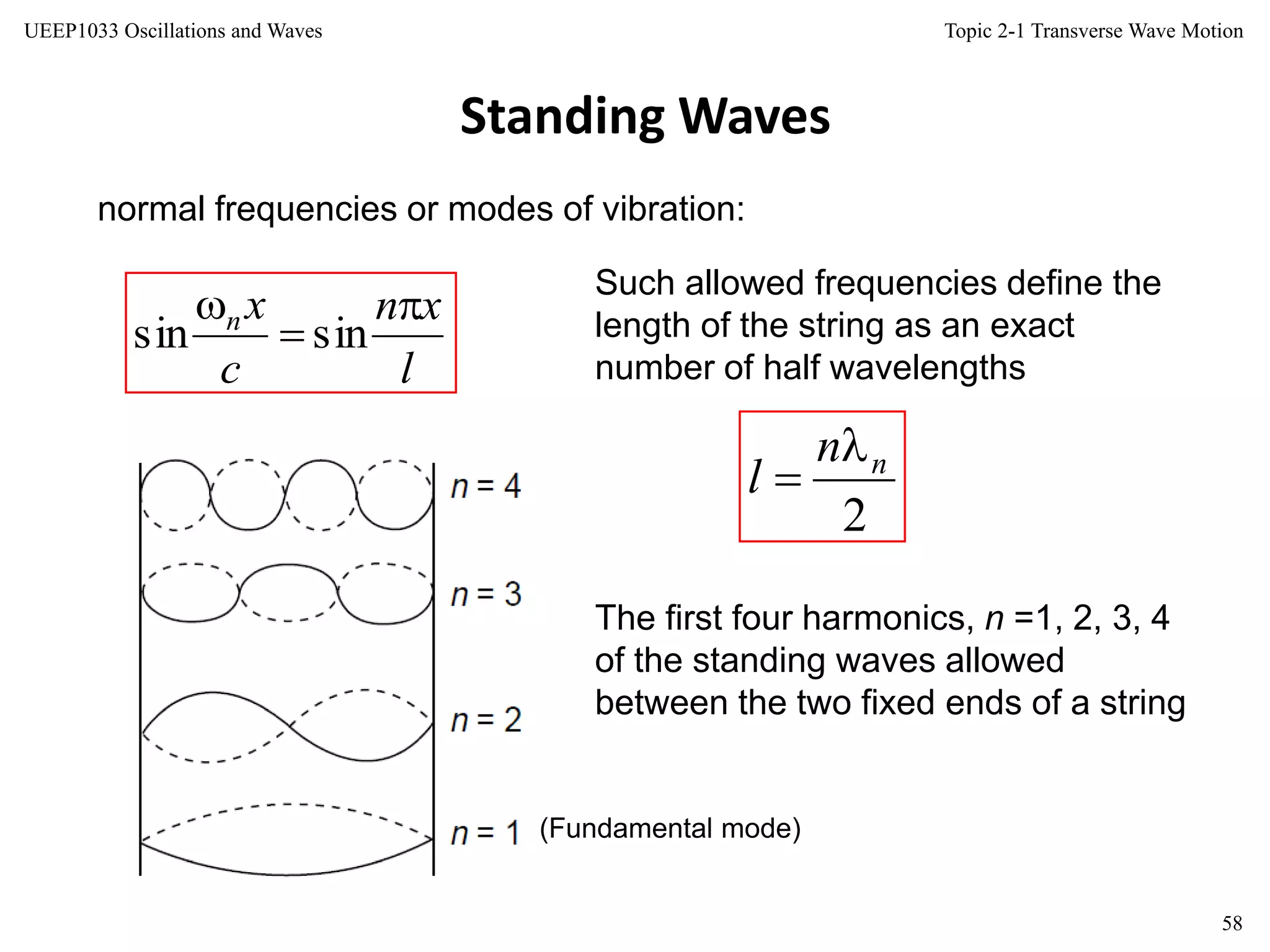
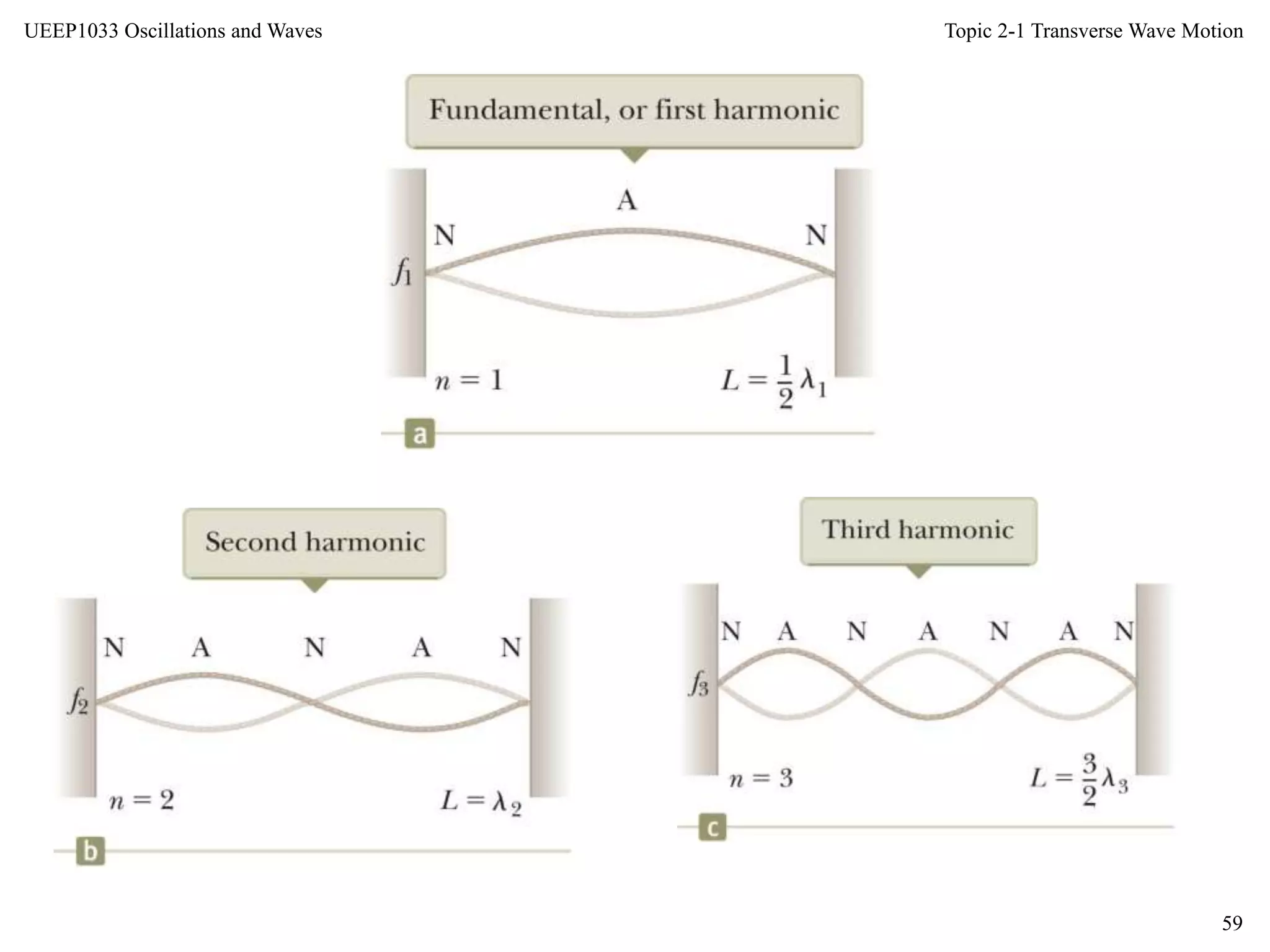
Any shape f (x) of the string with fixed end points [f (0) = f
(L) = 0] can be written as a superposition of these sine
functions with appropriate values for the coefficients A1, A2, .
. . , i.e. in the form
Amplitudes of Normal Modes
Fourier series](https://image.slidesharecdn.com/topic4transversewave-140705124742-phpapp02/75/Topic-4-transverse-wave-84-2048.jpg)