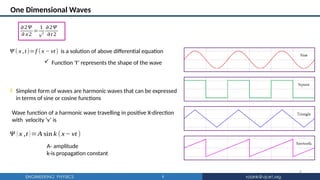
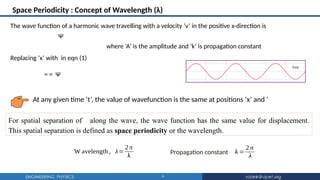
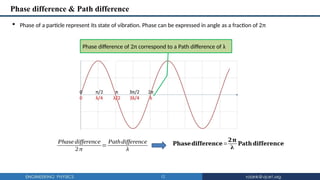
The document discusses the fundamental concepts of waves in physics, including definitions, types (transverse and longitudinal), and mathematical descriptions through wave functions. It explains key characteristics such as wavelength, period, phase differences, and provides equations for one-dimensional and three-dimensional waves. Additionally, it covers the behavior of transverse vibrations in a stretched string, leading to the derivation of wave equations and laws governing vibrations related to tension, length, and mass density.

1. 1
WAVES
Engineering Physics
Module I

2. Waves
2
A wave is a disturbance that propagates in space and transfers energy
without transfer of matter.

3. A transverse wave is a wave in which particle in the medium oscillates perpendicular to the direction of propagation of
the wave
Transverse Wave
3
Transverse wave travels in the form of crests and troughs. A wave’s crests are the highest points (points of maximum
upward displacement). On the other hand, the troughs of a wave are the lowest points (points of maximum downward
displacement).
Ex: e.m. waves, wave in a stretched string

4. Longitudinal Wave
4
A longitudinal wave is a wave in which particles of the medium oscillates parallel to the direction propagation of the wave.
A compression occurs when the wave compresses particles of the medium (pushes them close together). On the other
hand, a rarefaction is a region where the particles in medium spreads out (particles separate).
Ex: sound

5. Transverse & Longitudinal Waves
5
Transverse Wave Longitudinal Wave
Particle in the medium oscillates perpendicular
to the direction of propagation of the wave
Particle in the medium oscillates parallel to the
direction of propagation of the wave
Travels in the form of crests and troughs Travels in the form of compressions and
rarefactions
Can be polarised Cannot be polarized
Ex: e.m. waves, wave in a stretched string Ex: sound

6. 6
Wave Function
 Wave function is mathematical description of waves as a function of position and time co-ordinates
6
 It describes the displacement of particles in the medium at any position and time
Note: Displacement need not be physical displacement. Ex: electromagnetic wave

7. 7
One Dimensional Waves
Wave travelling along a line or an axis is known as one dimensional wave. Ex: waves through a string
Consider a one dimensional wave travelling along positive X-direction with velocity ‘v’. Its wave function is
Ψ ( x,t)=f (x − vt)
For a one dimensional wave travelling along negative X-direction
Ψ ( x,t)=f (x+vt)
General one dimensional wave function is
Ψ ( x,t)=f (x ± vt)
7
𝜕 2𝛹
𝜕 𝑥 2
=
1
𝑣
2
𝜕 2 𝛹
𝜕 𝑡 2 Differential equation of one dimensional wave

8. 8
One Dimensional Waves
Ψ ( x,t)=f (x − vt) is a solution of above differential equation
𝜕2Ψ
𝜕 x2
=
1
v
2
𝜕2Ψ
𝜕t 2
8
 Function ‘f’ represents the shape of the wave
 Simplest form of waves are harmonic waves that can be expressed
in terms of sine or cosine functions
Wave function of a harmonic wave travelling in positive X-direction
with velocity ‘v’ is
Ψ ( x ,t )=A sin k (x− vt )
A- amplitude
k-is propagation constant

9. 9
Space Periodicity : Concept of Wavelength (λ)
The wave function of a harmonic wave travelling with a velocity ‘v’ in the positive x-direction is
Ψ
where ‘A’ is the amplitude and ‘k’ is propagation constant
For spatial separation of along the wave, the wave function has the same value for displacement.
This spatial separation is defined as space periodicity or the wavelength.
Replacing ‘x’ with in eqn (1)
= = Ψ
At any given time ‘t’, the value of wavefunction is the same at positions ‘x’ and ‘
W avelength, λ=
2π
k
k=
2π
λ
Propagation constant

10. 10
Time Periodicity : Concept of Period (T)
This means the wave function has same displacement in a same position in space, after a
time interval of .
The wave function of a harmonic wave travelling with a velocity ‘v’ in the positive x-direction is
Ψ
where ‘A’ is the amplitude and ‘k’ is propagation constant
Replacing ‘t’ with
= = Ψ
Time interval after which the wavefunction has the same value at a given position is known as
period of the wave and is represented by ‘T’.
T =
2 π
kv

11. 11
T =
2 π
kv
=
ω=kv
kv =2 πν
2 π
λ
v =2 πν
v=
k =
2 π
λ
Here three waves have same velocity, but different
wavelength. Observe how many crests and troughs
are passing through this point for each wave in the
same interval of time.
Wave Velocity

12. Phase difference & Path difference
12
 Phase of a particle represent its state of vibration. Phase can be expressed in angle as a fraction of 2π
Phasedifference
2π
=
Pathdifference
λ
𝐏𝐡𝐚𝐬𝐞𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞=
𝟐𝛑
𝛌
𝐏𝐚𝐭𝐡 𝐝𝐢𝐟𝐟𝐞𝐫𝐞𝐧𝐜𝐞
Phase difference of 2π correspond to a Path difference of λ

13. 13
Three Dimensional waves
Wave travelling in all directions is known as three dimensional wave. The wave function of such a wave is a function of
three position and time coordinates.
Ψ =f (x , y ,z ,t)
Differential equation of three dimensional wave is
𝜕 2Ψ
𝜕 x 2
+
𝜕 2 Ψ
𝜕 y 2
+
𝜕 2 Ψ
𝜕 z 2
=
1
v
2
𝜕 2Ψ
𝜕 t 2
∇ 2 Ψ =
1
v2
𝜕2Ψ
𝜕t 2 ∇2=
𝜕2
𝜕 x 2
+
𝜕2
𝜕 y 2
+
𝜕2
𝜕 z2
Ψ =a e
± i(𝐤 .𝐫 − ω t)
+
|𝐤|=√kx
2
+ ky
2
+ kz
2
+
Ψ =asin (𝐤 .𝐫 − ωt )
Ψ =a cos(𝐤 .𝐫 −ω t)
Solution is
where propagation vector
position vector

14. Transverse Vibrations in a Stretched String
14
 Consider a string of length l kept stretched between points A and B by tension T.
 Harmonic vibrations are set by plucking the string at the centre and releasing it free.
 Let the normal position of string be along x-axis and it is plucked in y-direction.
 A small element PQ of the string with length x make angles  and - with x-
axis.
T
P
Q
θ
θ-δθ
δx
A B
T
Y
X
l

15. 15
T
sinθ
T
sin(θ-
δθ)
T cos(θ- δθ)
T cosθ
Transverse Vibrations in a Stretched String
15
Downward component of Tension at point P = T sinθ = T tanθ
{For small values of θ; tanθ= sinθ }
Rate of change of slope with respect to the length of the element =
tan θ=
dy
dx
Downward component of Tension at point P =
; is the slope at P

16. 16
Transverse Vibrations in a Stretched String
16
Downward component of Tension at point P For small values of θ; T sinθ = T tanθ
Rate of change of slope with respect to the length of the element =
Change in slope from point P to Q = x
Slope at Q = - x
T
sinθ
T cosθ

17. 17
Transverse Vibrations in a Stretched String
17
Resultant downward tension; F=T
dy
dx
−T
[dy
dx
−
d2 y
dx 2
δ x
]
¿ T
[ dy
dx
−
d 2 y
dx 2
δ x
]
¿T
dy
dx
−T
dy
dx
+T
d 2 y
dx2
δ x
F=T
d 2 y
dx 2
δ x------------------------------------------------------------------------------(1)
T
sinθ
T
sin(θ-
δθ)
T cos(θ- δθ)
T cosθ
Upward component of Tension at Q = T tan (θ - δθ)

18. 18
Let ‘m’ be the mass per unit length of the string. Then mass of the element PQ is mδx
Transverse Vibrations in a Stretched String
Force acting on the element : F=m δ x
d 2 y
d t 2
-------------------------(2)
From equations (1) and (2)
=
= -------------------------(3)
Equation (3) is similar to one dimensional wave equation.
d 2Ψ
dt 2
=v 2
d 2 Ψ
dx 2
-------------------------(4)
Eqn (3) is known as wave equation of a string. Comparing equations (3) and (4)
v=
√T
m v - is the velocity of the wave

19. Transverse Vibrations in a Stretched String
19
In case of fundamental mode of vibration λ = 2l
If ν is the frequency of vibration of the string, then using the relationship v=
ν =
v
λ
ν=
1
λ √T
m
ν=
1
2𝑙 √T
m
ν=
p
2𝑙 √T
m
General equation for different modes of vibration of string is
Where p=1,2,3…
p=1 -Fundamental mode
P=2 -First overtone
P=3 - Second overtone

20. 20
• The Law of Length: The fundamental frequency of vibration is inversely proportional to
the length of the string, when linear mass density and tension are kept constant.
• The Law of Tension: The fundamental frequency of vibration is directly proportional to
square root of the tension in the string, when linear mass density and length are kept
constant
• The Law of Mass: The fundamental frequency of vibration is inversely proportional to
square root of linear mass density, when tension and length are kept constant
Laws of Transverse Vibrations