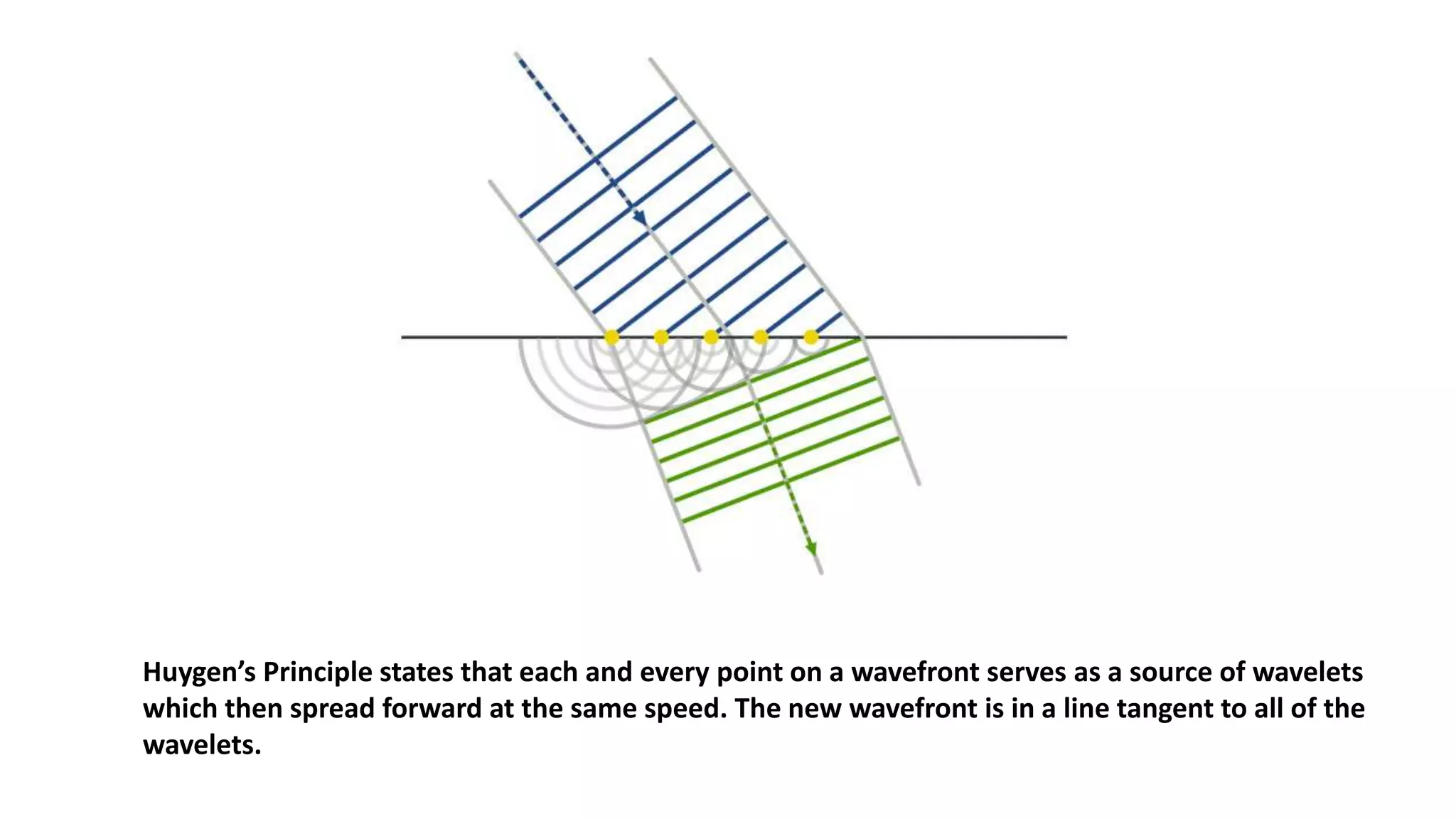
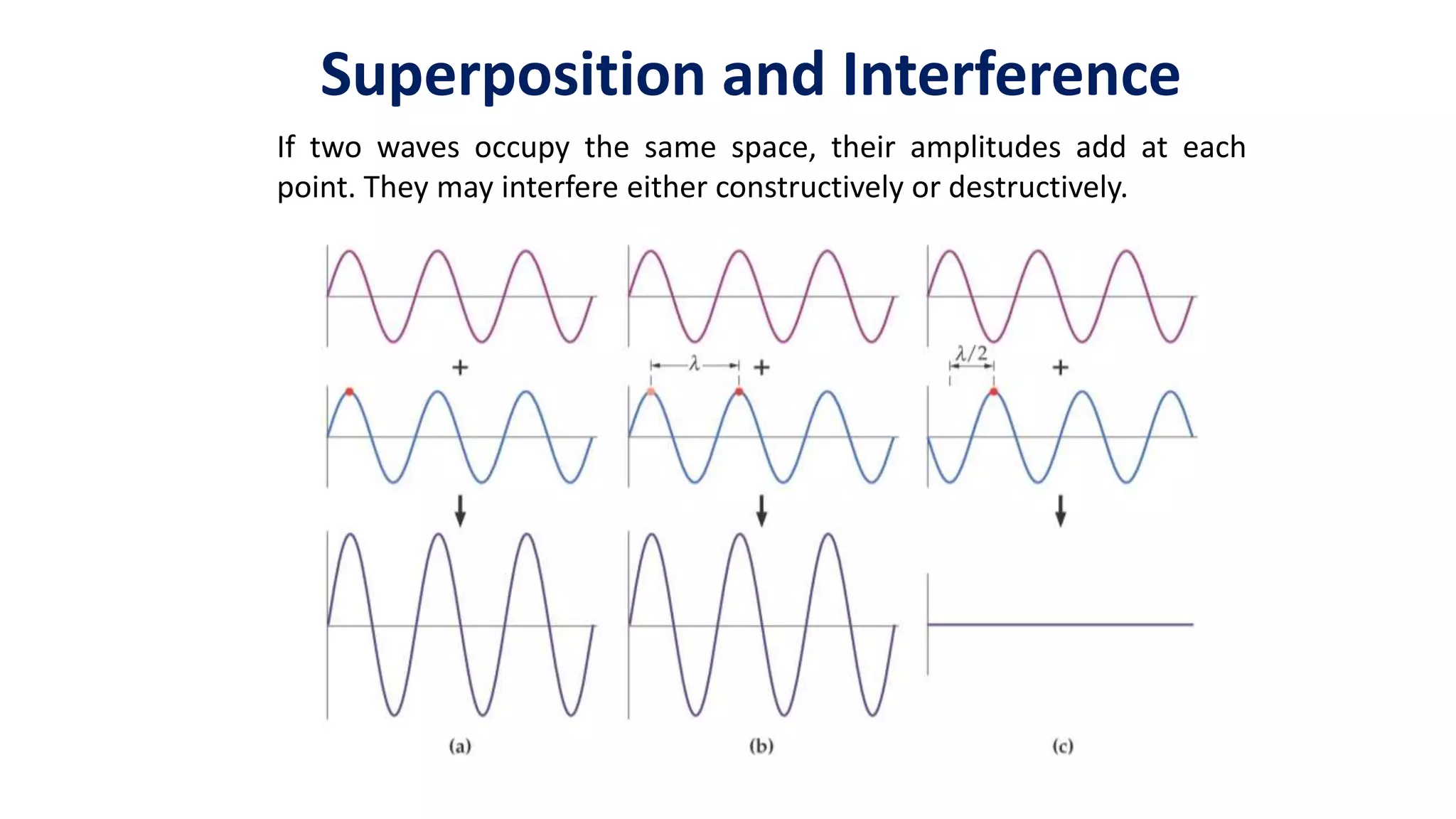
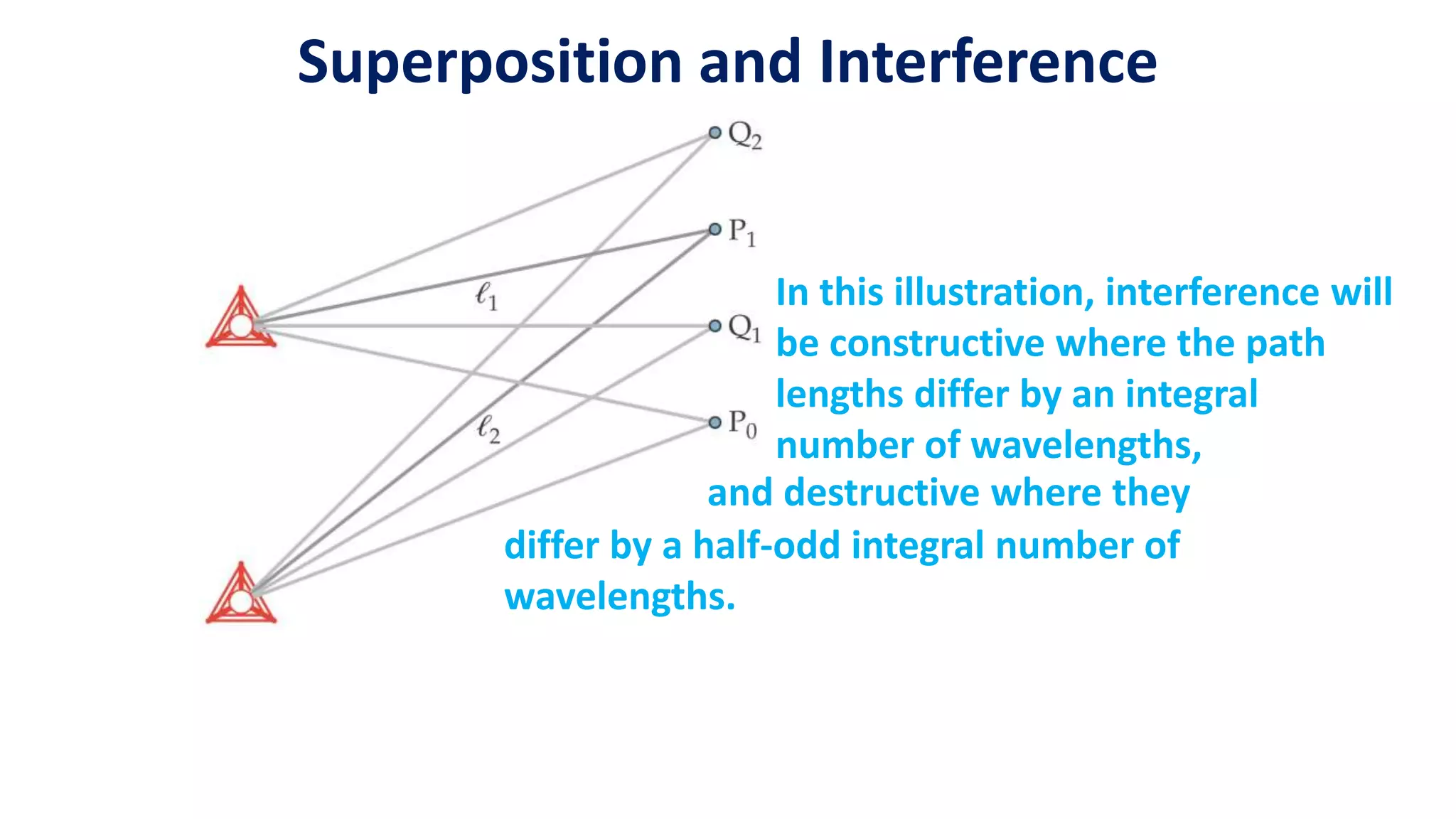
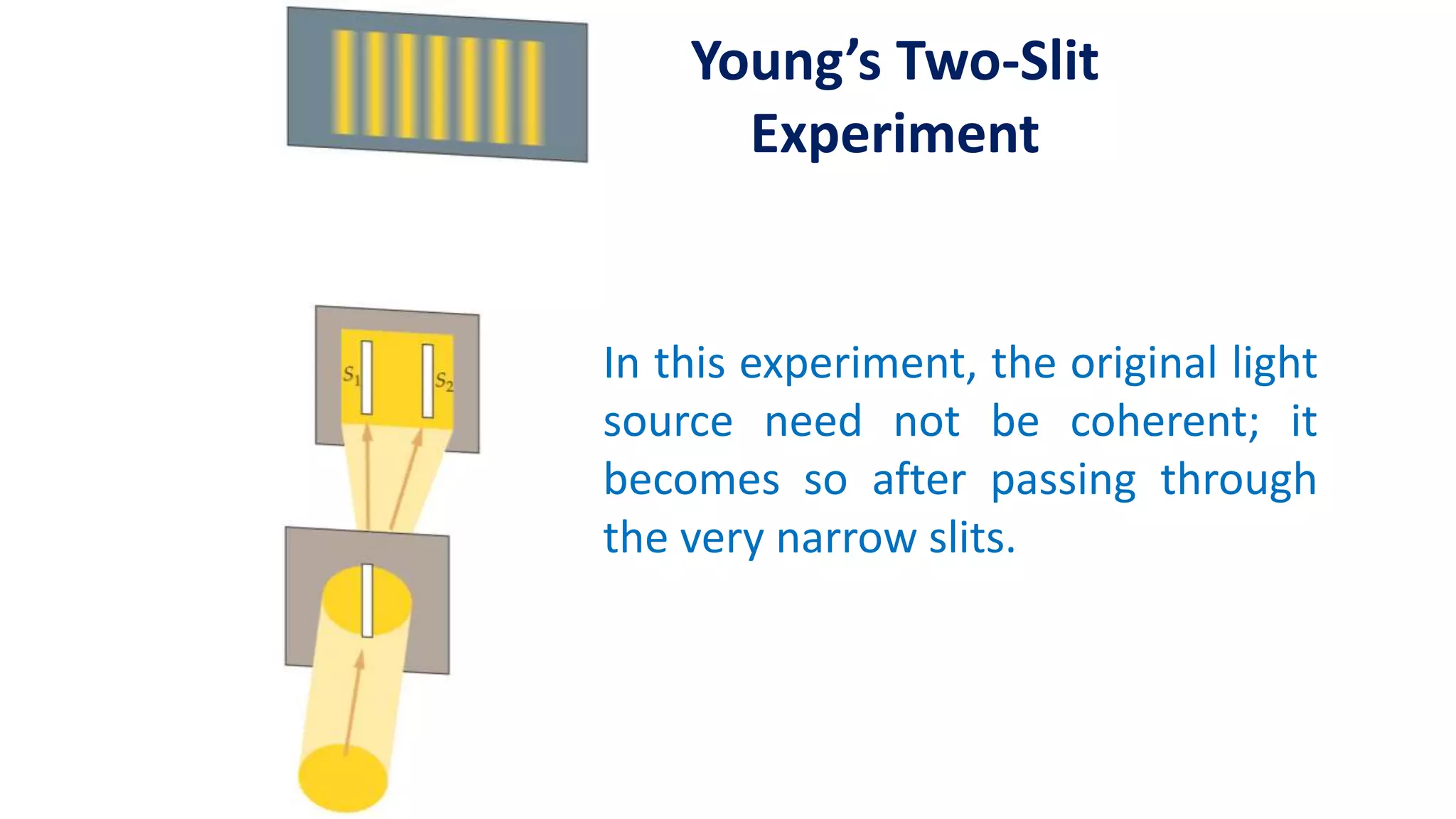
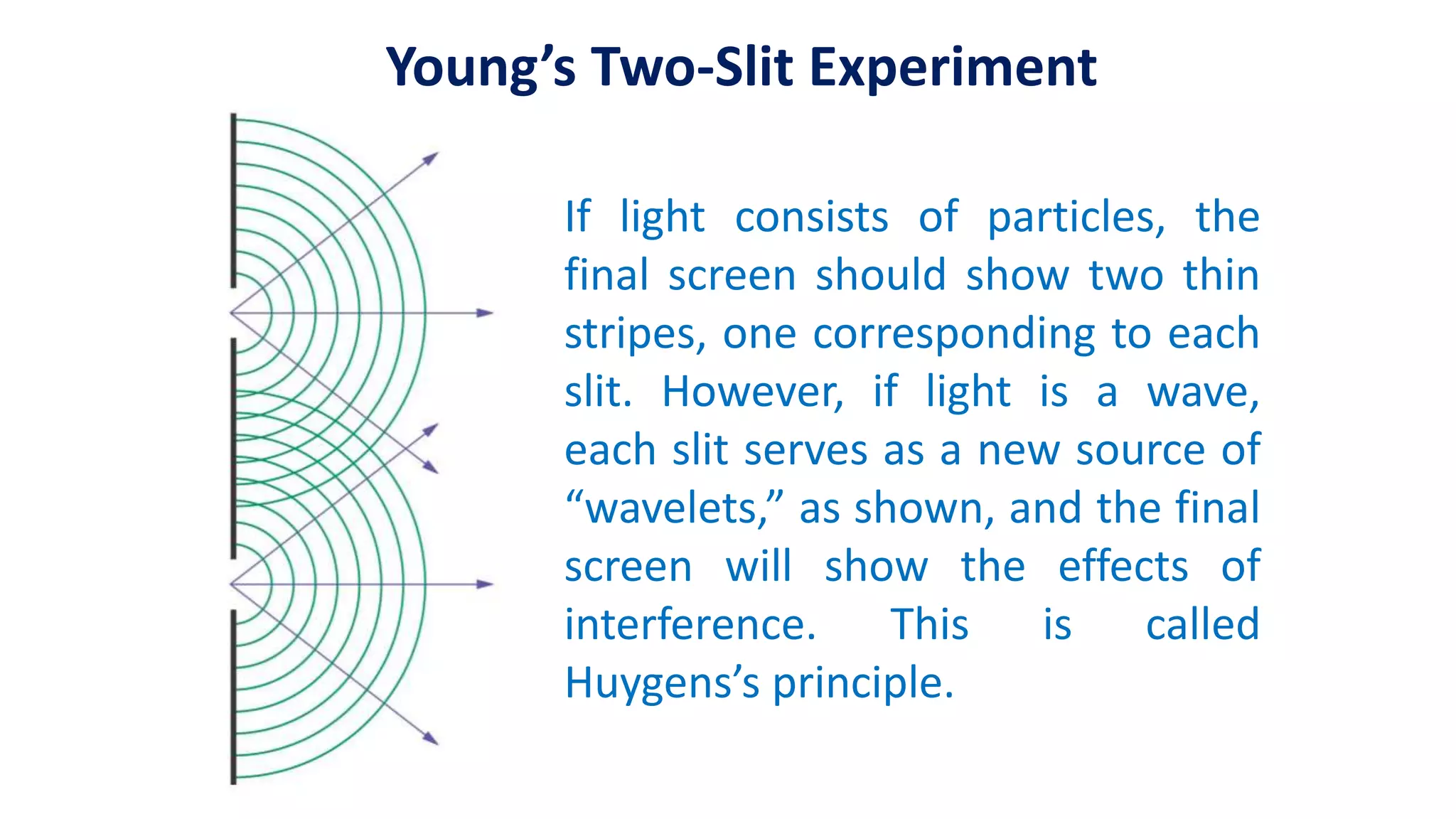
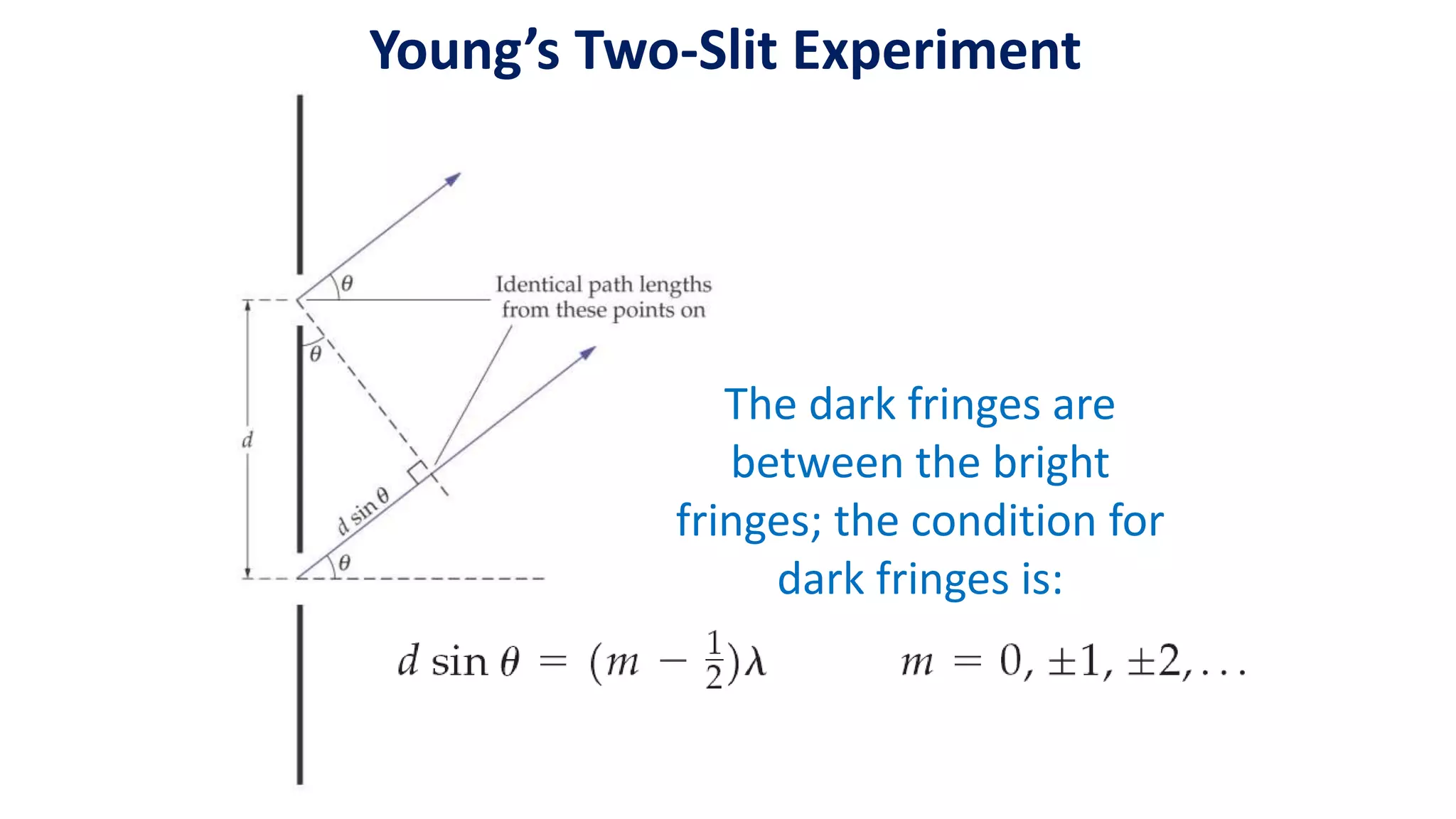
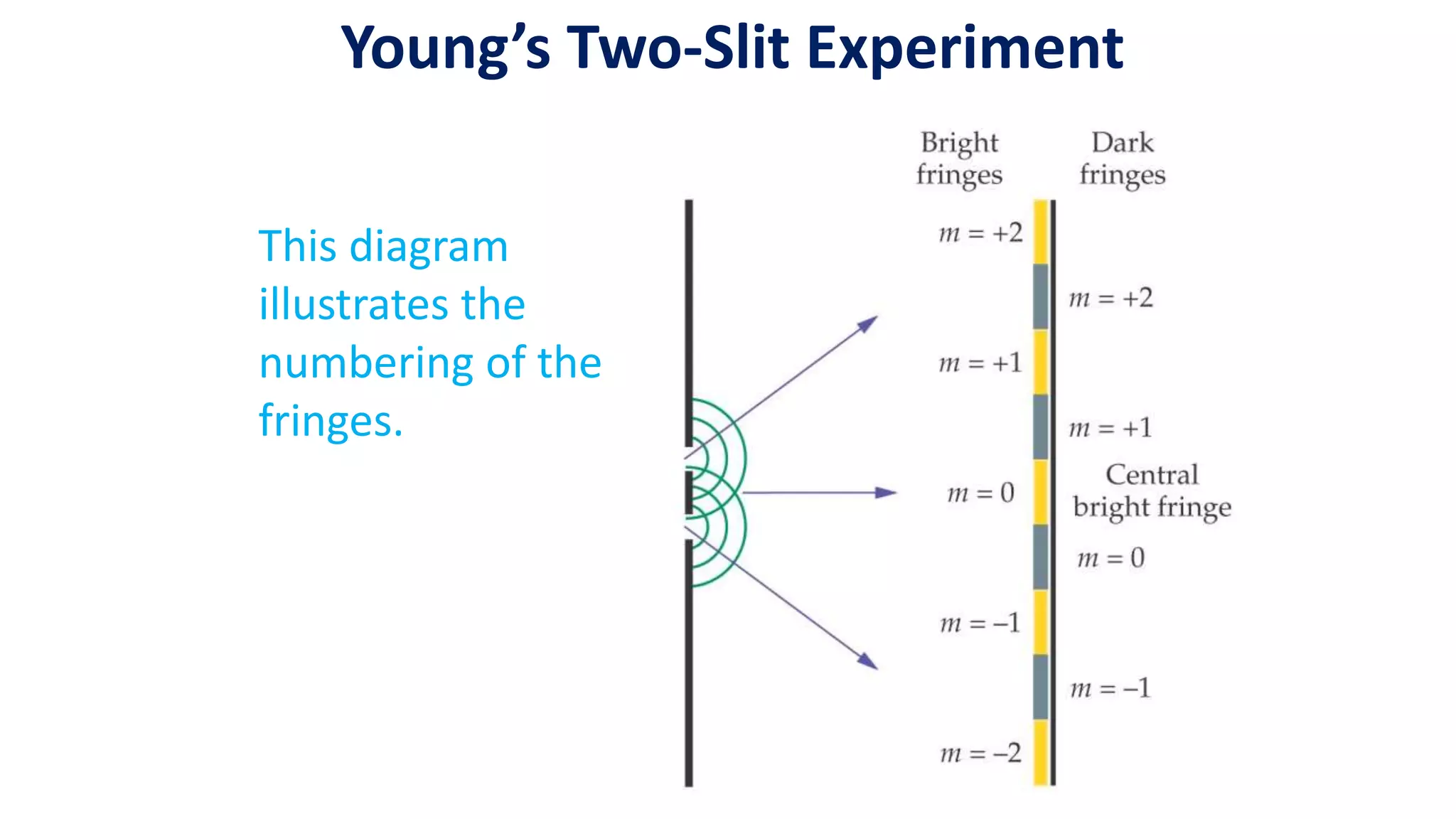
This presentation by Mainul Hossan covers key concepts in optics, including Huygen's principle, superposition, and interference of waves, as well as Young's two-slit experiment. Huygen's principle states that every point on a wavefront acts as a source for spherical wavelets, which can explain refraction and interference phenomena. The presentation highlights that interference patterns arise from the overlapping of waves, leading to constructive and destructive interference, as demonstrated in Young's experiment.

1. Presented By
Mainul Hossan
Roll: 2450
Department of Physics,
Jahangirnagar university.
Course Name: OPTICS
Course Code: PH-202
Course Instructor: Asst. Prof. Shariful Islam
WELCOME TO MY PRESENTATION

2. OUTLINE OF THE PRESENTATION
1)Huygen’s principle.
2)Superposition & Interference of waves
3)Young’s experiments.

3. Huygen’s principle
Christiaan Huygens
 A seventeenth-century Dutch mathematician
and scientist (physicist, astronomer,
probabilist, horologist).
 In 1678, Huygens proposed that every point
on the wave front of a wave was a source of
a spherical wave.
 The resultant wave is determined by adding
all the waves from the point sources.

4. Huygen’s Principle states that each and every point on a wavefront serves as a source of wavelets
which then spread forward at the same speed. The new wavefront is in a line tangent to all of the
wavelets.

5. USES OF HUYGEN’S PRINCIPLE
1. It can be used to explain the phenomenon of refraction
and interference.
2. It helps in explaining the linear and spherical wave
propagation.
LIMITATIONS OF HUYGEN’S PRINCIPLE
1. It is a consequence of the homogeneity of space (the space is said
to be uniform in all the locations).
2. It was noticed by Jacques Hadamard in 1900, that Huygen’s
principle could not be applied when the number of spatial
dimensions was equal

6. Superposition and Interference
If two waves occupy the same space, their amplitudes add at each
point. They may interfere either constructively or destructively.

7. Superposition and Interference
 Interference is only noticeable if the light sources are
monochromatic (so all the light has the same
wavelength) and coherent (different sources maintain
the same phase relationship over space and time).
 If this is true, interference will be constructive where the
two waves are in phase, and destructive where they are
out of phase.

8. Superposition and Interference
In this illustration, interference will
be constructive where the path
lengths differ by an integral
number of wavelengths,
and destructive where they
differ by a half-odd integral number of
wavelengths.

9. Superposition and Interference
To summarize, the two path lengths l1 and l2 will
interfere constructively or destructively according
to the following:

10. Young’s Two-Slit
Experiment
In this experiment, the original light
source need not be coherent; it
becomes so after passing through
the very narrow slits.

11. Young’s Two-Slit Experiment
If light consists of particles, the
final screen should show two thin
stripes, one corresponding to each
slit. However, if light is a wave,
each slit serves as a new source of
“wavelets,” as shown, and the final
screen will show the effects of
interference. This is called
Huygens’s principle.

12. Young’s Two-Slit Experiment
As the pattern on the screen shows, the light on the screen has alternating
light and dark fringes, corresponding to constructive and destructive
interference.
The path difference is given by:
Therefore, the condition for bright fringes (constructive interference) is:

13. Young’s Two-Slit Experiment
The dark fringes are
between the bright
fringes; the condition for
dark fringes is:

14. Young’s Two-Slit Experiment
This diagram
illustrates the
numbering of the
fringes.

15. Any query?