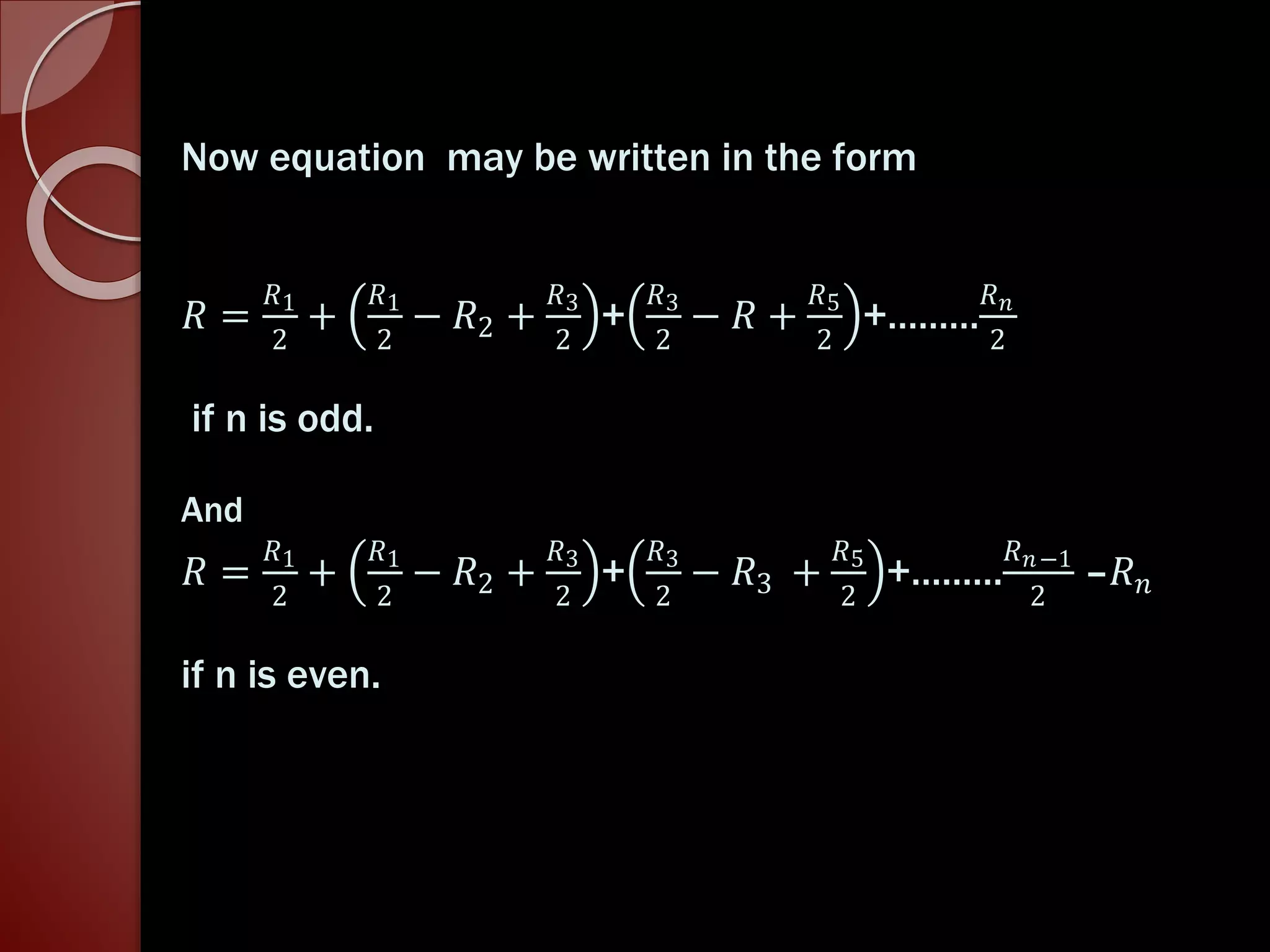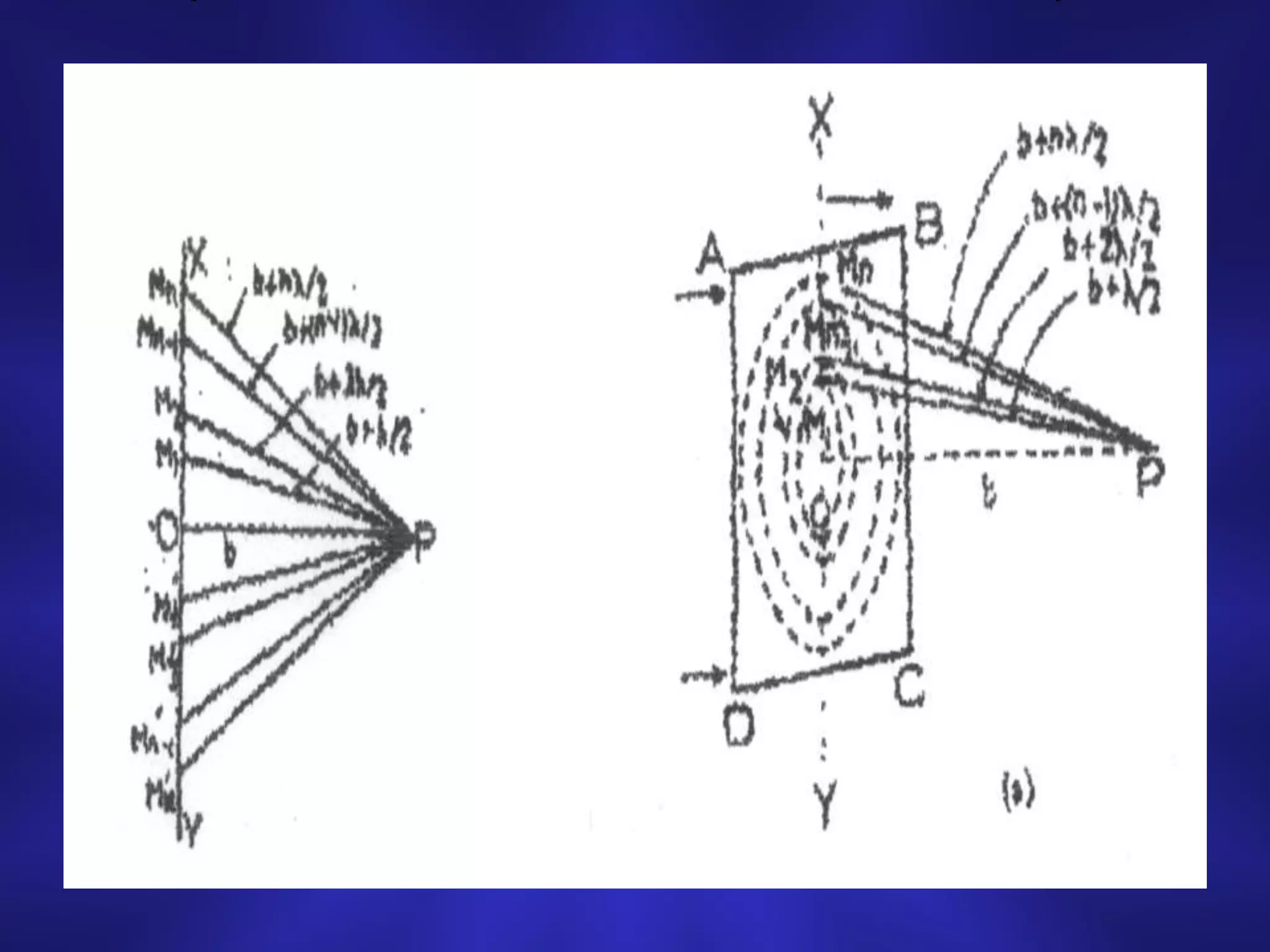
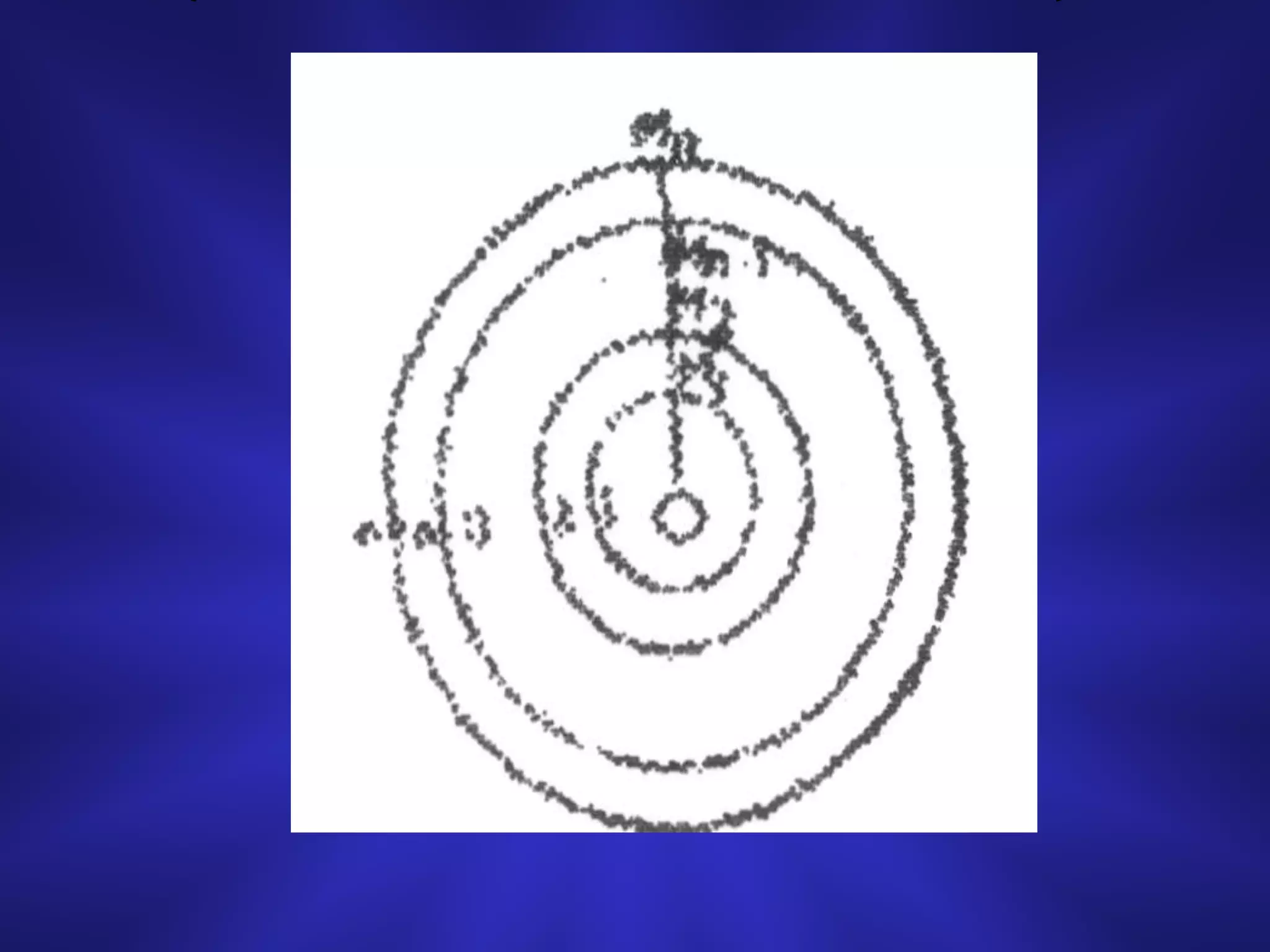
1) Fresnel's theory of diffraction explains that diffraction occurs due to the interference of secondary wavelets produced by unobstructed portions of the wavefront. 2) When considering the diffraction pattern at a point P, Fresnel divided the wavefront into concentric half-period zones centered on the point's pole O. The contribution of each zone to the intensity at P depends on the zone's area and distance from P. 3) For a large number of zones, the total intensity at P is approximately one fourth of that due to the first zone alone, explaining the dimming of light in diffraction patterns.

1. POWER POINT PRESENTATION
TOPIC FRESNEL'S THEORY
OF
DIFFRACTION
BY:- PROF.S.V.ANGADI,
PHYSICS DEPARTMENT,
J.T.COLLEGE, GADAG

3. FRESNEL'S EXPLANATION
• The diffraction phenomenon is caused by
the interference of innumerable secondary
wavelets produced by the unobstructed
portions of the same wave-front.

4. i) Each element of a wave-front sends secondary
waves continuously.
ii) A wave front can be divided into a large number of
strips or zones called the Fresnel's zones
ii)The resultant effect at any external point P is
determined by combining the effects of all the
secondary waves reaching them from various zones.
iv) The effect at a point due to any particular zone
depends on the distance of the point from the
zone.
v) The effect at any point P depends on the
inclination of the point with reference to zone
under consideration. The intensity is maximum
along a direction normal to the zone and decreases
as the angle of inclination Increases.

5. FRESNEL'S HALF PERIOD
FOR A PLANE WAVE :
• Let ABCD be a section of a plane wave-
front of monochromatic light of wave
length , traveling from left to right (fig).
Let P be an external point at which the
effect of the entire wave-front is desired.

7. Let OP is perpendicular drawn from P to the wave-front and is equal to b. To
find the resultant intensity at P due to the wave-front, by Fresnel’s method,
the wave-front is divided In to a number of concentric half period zones
called “Fresnel's zone." and then the effect of all the zones at point p is
found. This can be done as follows: Considering P as centre and radii equal
to b+𝜆/2, b+2𝜆/2, b+3𝜆/2,... etc. draw a series of spheres on the wave-front
thus cutting the wave-front into annular strips or zones. The sections of
these spheres by the plane wave-front are concentric circles having
common centre O and radii 0𝑀1
, 0𝑀2
, 0𝑀3
...0𝑀 𝑛−1
, 0𝑀 𝑛
......etc.

8. The secondary wavelets from any two consecutive zones reach P with a
path difference 𝜆/2 or time difference half period. That is why the zones
arecalledhalfperiodzones.THEareaoftheinnermost(first)circleiscalled
firsthalfperiodzone;similarlytheannularareabetweenthefirstcircleand
the second circle is called second half period zone and so on. Thus the
annularareabetween(n-1)th andnthcircleiscallednthhalfperiodzone.
The point O is called the pole of the wave-front with respect to point P. A
Fresnel half period zone with respect to an external point P is a thin
annularzoneorathinstripoftheprimarywave-frontsurroundingthepoint
O such that the distances of its outer and inner edges from O differs by
𝜆/2.

9. RADII OF HALF PERIOD
ZONE:
The radius of first half period zone,
OM1 = M1P 2 − OP 2
OM1 = b +
λ
2
2
− b2
OM1 = b2 +
λ
4
2
+ bλ − b2
OM1 = bλ ,As b >> 𝜆

11. The radius of second half period
zone,
OM2 = M2P 2 − OP 2
OM2 = b+
2λ
2
2
−b2
OM2 = b2 +
4λ
4
2
+2bλ−b2
OM2 = 2bλ

12. OMn = MnP 2 − OP 2
OMn = b +
nλ
2
2
− b2
OMn = b2 +
(nλ)
4
2
+ nbλ − b2
OMn = nbλ
Thus we see that the radii of half period zones are proportional to the
square root of the natural numbers.

13.  As area of nth zone is independent of n, thus the area
of each half period zone is approximately the same and
is equal More accurately the area of the zone increases
slightly with n.
The area of n zone
= π OMn
2
− OMn−1
2
= π PMn
2
− PO 2
− π PMn−1
2
− PO 2
= π b +
nλ
2
2
− b 2
− π b +
(n−1)λ
2
2
− b 2
= π b2
+
nλ 2
4
+ bnλ − b2
− π b2
+
(n−1)λ 2
4
+ b n − 1 λ − b2
= π
nλ 2
4
+ bnλ − π
(n − 1)λ 2
4
+ b n − 1 λ
= π nλ +
λ2
4
2n − 1
= πbλ

14. THE DISTANCE OF THE POINT
FROM THE HALF PERIOD
ZONE:
Theaveragedistanceofnth
halfperiodzonefrompointP,
=
b+
nλ
2
++b+(n−1)
λ
2
2
=b+(2n−1)
λ
4

15. THE AMPLITUDE OF THE
DISTURBANCE AT P DUE TO
AN INDIVIDUAL ZONE :
The amplitude of the disturbance due to a given zone is
(i) Directly proportional to the area of the zone because number
of point sources, from each of which a secondary wavelet
starts, in a zone are proportional to the area,
(ii) Inversely proportional to the distance of the point P from the
given zone.
(iii) Directly proportional to the obliquity factor (1+cos 𝜃) whose
𝜃is the angle between the normal to the zone and the line
joining the zone to point P.

16. Thus amplitude of the disturbance at P due to 𝑛𝑡ℎ
zone is,
𝑅𝑛 𝛼
𝜋 𝑏𝜆 +
𝜆2
2𝑛 − 1
4
𝑏 +
2𝑛 − 1 𝜆
4
1 − 𝑐𝑜𝑠𝜃𝑛
𝑅𝑛 𝛼 𝜋𝜆 1 − 𝑐𝑜𝑠𝜃𝑛
As n increases, 𝜃𝑛 increases and cos 𝜃𝑛 decreases. Thus the amplitude of
the disturbance at P due to a given zone decreases as the order of the zone
increases. This means that the amplitude of the disturbance due to first
half period zone is maximum and it decreases regularly as we pass from
the inner zone to the next outer.

17. Let 𝑅1,𝑅2, 𝑅3,…..𝑅𝑛 betheamplitudesofthedisturbancesatP,duetothe
first second, third...., nth half period zones respectively. The magnitudes of
𝑅1,𝑅2 etc are of continuously in decreasing order. As the path difference
between the wave reaching P from any two consecutive half-period zones
is 𝜆/2, the waves from two consecutive zones reach P in the opposite
phase.

18. Therefore if amplitude due to first zone is positive, that due to second
zone is negative, that due to third zone is positive and so on, i e 𝑅1, 𝑅3,
…..𝑅 𝑛−1 etc are positive and 𝑅2, 𝑅4, …..𝑅 𝑛 etc, are negative Hence the
resultant amplitude at P due to the entire wave front is
𝑅 = 𝑅1 − 𝑅2 + 𝑅3,… . (−1)n−1
𝑅 𝑛
As the magnitudes of successive terms 𝑅1, 𝑅2, 𝑅3, …..𝑅 𝑛 decrease
gradually, 𝑅2slightly less than 𝑅1 and greater than 𝑅3 so that we may
write,
𝑅2 =
𝑅1 + 𝑅3
2
𝑅3 =
𝑅2 + 𝑅5
2
And so on.

19. Now equation may be written in the form
𝑅 =
𝑅1
2
+
𝑅1
2
− 𝑅2 +
𝑅3
2
+
𝑅3
2
− 𝑅 +
𝑅5
2
+………
𝑅 𝑛
2
if n is odd.
And
𝑅 =
𝑅1
2
+
𝑅1
2
− 𝑅2 +
𝑅3
2
+
𝑅3
2
− 𝑅3 +
𝑅5
2
+………
𝑅 𝑛−1
2
–𝑅 𝑛
if n is even.

20. In above relations the quantities in the bracket is very nearly equal to zero
hence we can write
𝑅 =
𝑅1
2
+
𝑅𝑛
2
𝑖𝑓 𝑛 𝑖𝑠 𝑜𝑑𝑑
𝑅 =
𝑅1
2
+
𝑅𝑛
2
𝑖𝑓 𝑛 𝑖𝑠 𝑒𝑣𝑒𝑛
But usually n is large, hence we may write 𝑅𝑛−1 (appro).then
𝑅𝑛−1
2
− 𝑅𝑛 = −
𝑅𝑛
2

21. So that above two equations may be represented by a single
equation as
𝑅 =
𝑅1
2
±
𝑅 𝑛
2
The plus and minus sign being taken accordingly as n is odd or
even. For large wave front, n is very large, hence Rn vanishes; so
that we can have
𝑅 =
𝑅1
2
Thus the amplitude due to a large wave front at a point in front of
it is half that due to the first half period zone acting alone. The
intensity at any point is proportional to the square of the
amplitude, therefore the resultant Intensity at P
𝐼𝛼
𝑅 𝑛
4
This means the intensity at appoint is one forth of intensity due to
the first half period zone alone.

22. EXPLANATION OF RECTILINEAR
PROPAGATION OF LIGHT:
 Let a plane wave-front of monochromatic light be
incident normally on a rectangular aperture
ABCD shown in figure. Let a screen be placed
parallel to the rectangular aperture at some
distance from it. Let A'B'C'D' (full line rectangle
on the screen) be the geometrical projection of
ABCD on the screen. If the law of rectilinear
propagation were strictly true, we would obtain
uniform illumination inside the full line rectangle
and uniform darkness outside it.

24.  Let us consider four typical points P1, P2, P3, P4 on the screen.
The corresponding poles are O1 O2, O3, &O4 respectively. The
point P1 is well inside the full rectangle. Its pole O1 is at large
distance from the edge of the aperture as compared with the
wavelength of light. Therefore if we draw half period zones with
O1, as centre, a large number of zones can be drawn before the
edge of the aperture is reached. Thus all the effective zones are
open and hence the resultant amplitude at is equal to half the
amplitude due to first half period zone. As the area of these half
period zones is extremely small, we can conclude that light from
O1 has traveled to P1 along a straight line. The points in the
neighborhood of P1 are similarly and uniformly illuminated.

25.  The point P2 is well inside the geometrical
shadow. Its pole is O2. If we draw half period
zones around O2, all the effective zones are
totally blocked and hence the resultant
amplitude at P2 is zero. Thus there is
complete darkness at P2.The point P3 Is
near the edge and inside the geometrical
projection. Its pole 01,is near the edge AD of
the aperture. If half period zones are drawn
around O3, they are partly cut off and the
areas of the zones change too rapidly so that
the above theory cannot be applied. Similarly
for point P4 which is near the edge and
outside the geometrical projection, the
intensity cannot be decided.

26.  Thus there is uniform illumination at all
points inside the inner dotted rectangle and
complete darkness at all points outside the
outer dotted rectangle. P1 points lying
between the two dotted rectangles, this
elementary theory gives no information. It
is certain that at these points here is
neither nether illumination nor complete
darkness. As the wavelength of light is very
small, the two dotted rectangles lie very
close to the full line rectangle. Thus
Fresnel’s wave theory accounts for
approximate rectilinear propagation of light

27. THE END