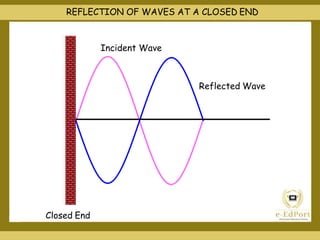
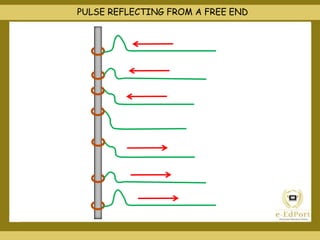
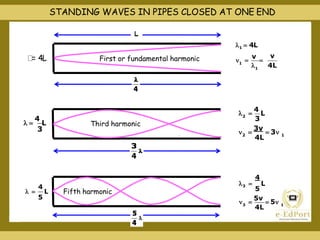
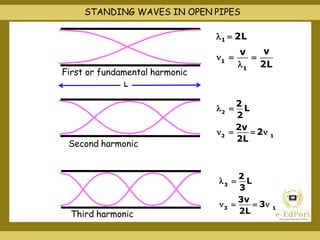
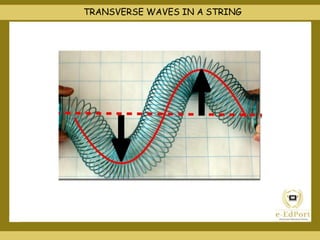
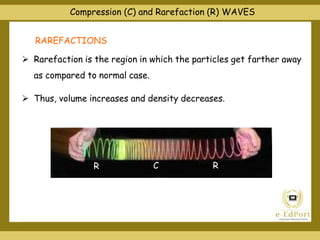
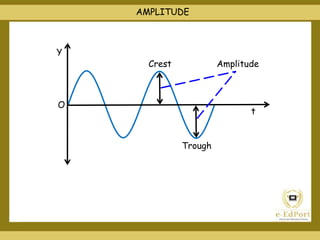
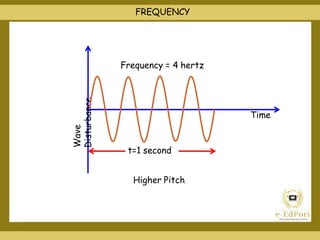
This document covers various topics related to waves including different types of waves, wave properties such as amplitude and wavelength, and concepts such as superposition, reflection, and standing waves. It discusses transverse and longitudinal waves, the displacement relation for progressive waves, and formulas for the speed of sound and waves on strings. Reflection at closed and open boundaries is examined, showing how the



























![SPEED OF A TRANSVERSE WAVE ON STRETCHED STRING
The speed of a transverse wave on stretched string depends
upon:
(i) Linear mass density of the string,
(ii) Tension T in the string
The dimension of is [ML-1].
The dimension of T is that of force that is [MLT-2].
-2
The ratio of
T
has the dimension
[MLT ]
= [L
2
T-2
]
μ [ML-1
]
So, if v depends only on T and μ the relation between
them must be v = C
So, v =
T
μ
It is observed that C = 1
T
μ](https://image.slidesharecdn.com/ch15waves-200716115423/85/Ch-15-waves-32-320.jpg)
![ It has been explained on the basis of Bulk Modulus B and
SPEED OF A LONGITUDINAL WAVE
density .
The dimension of Bulk modulus is [ML-1T-2] and that of
density is [ML-3].
On the basis of dimensional analysis, the expression for the
speed of Longitudinal Wave is
v = C
B
ρ
C is a dimensionless constant.
Thus, the speed of the longitudinal wave is
v =
B
ρ
(Since, C=1)](https://image.slidesharecdn.com/ch15waves-200716115423/85/Ch-15-waves-33-320.jpg)