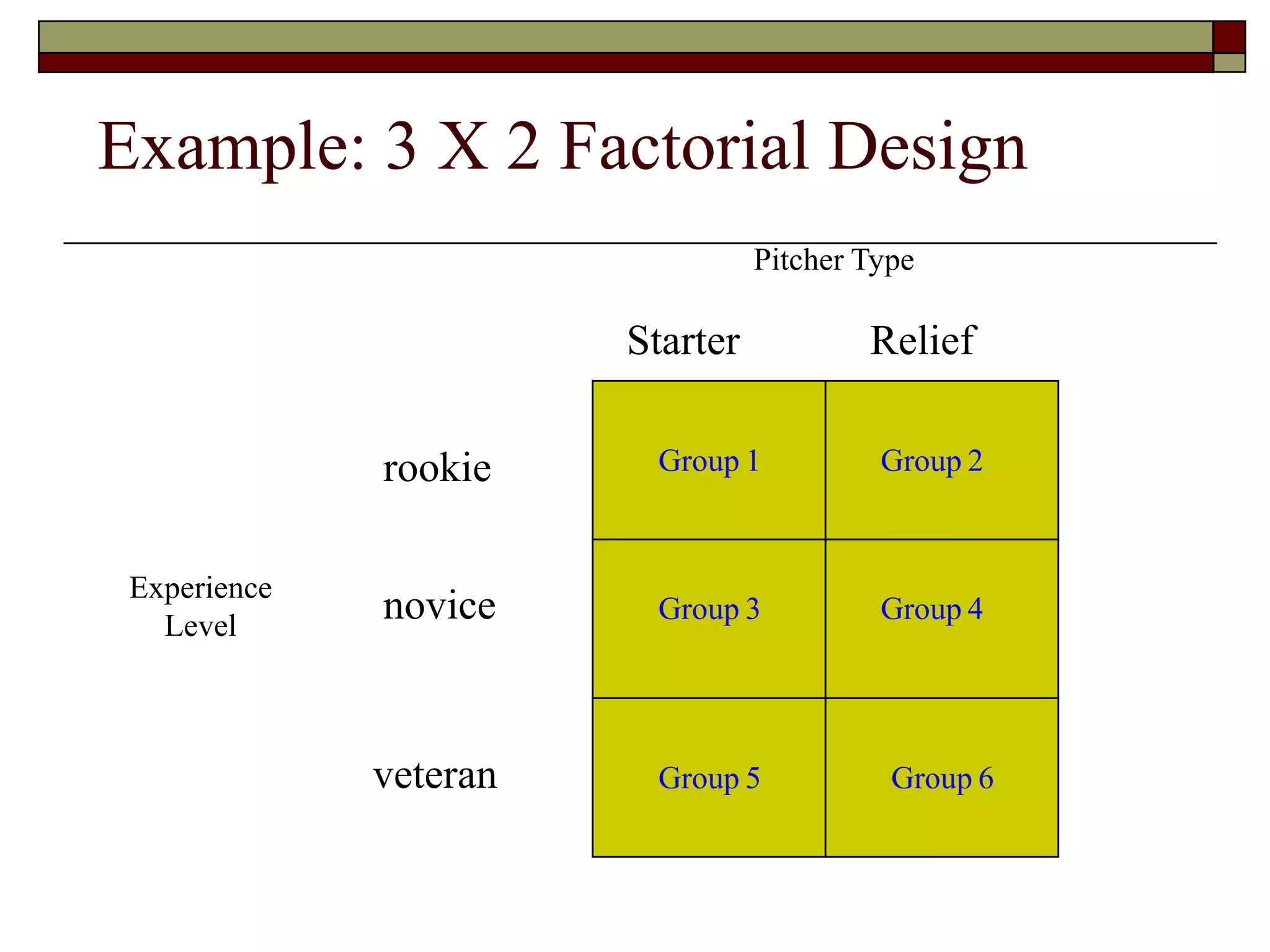
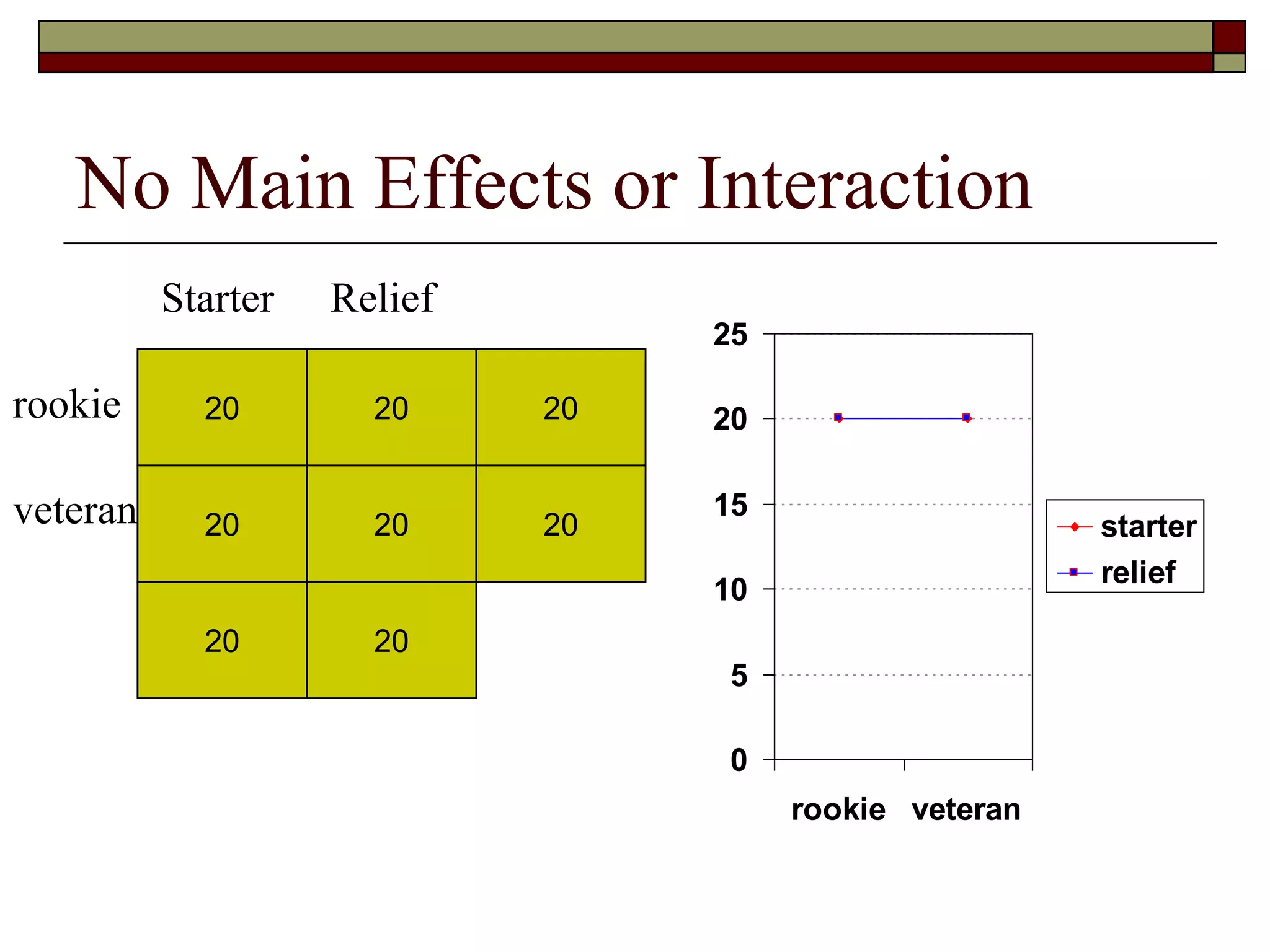
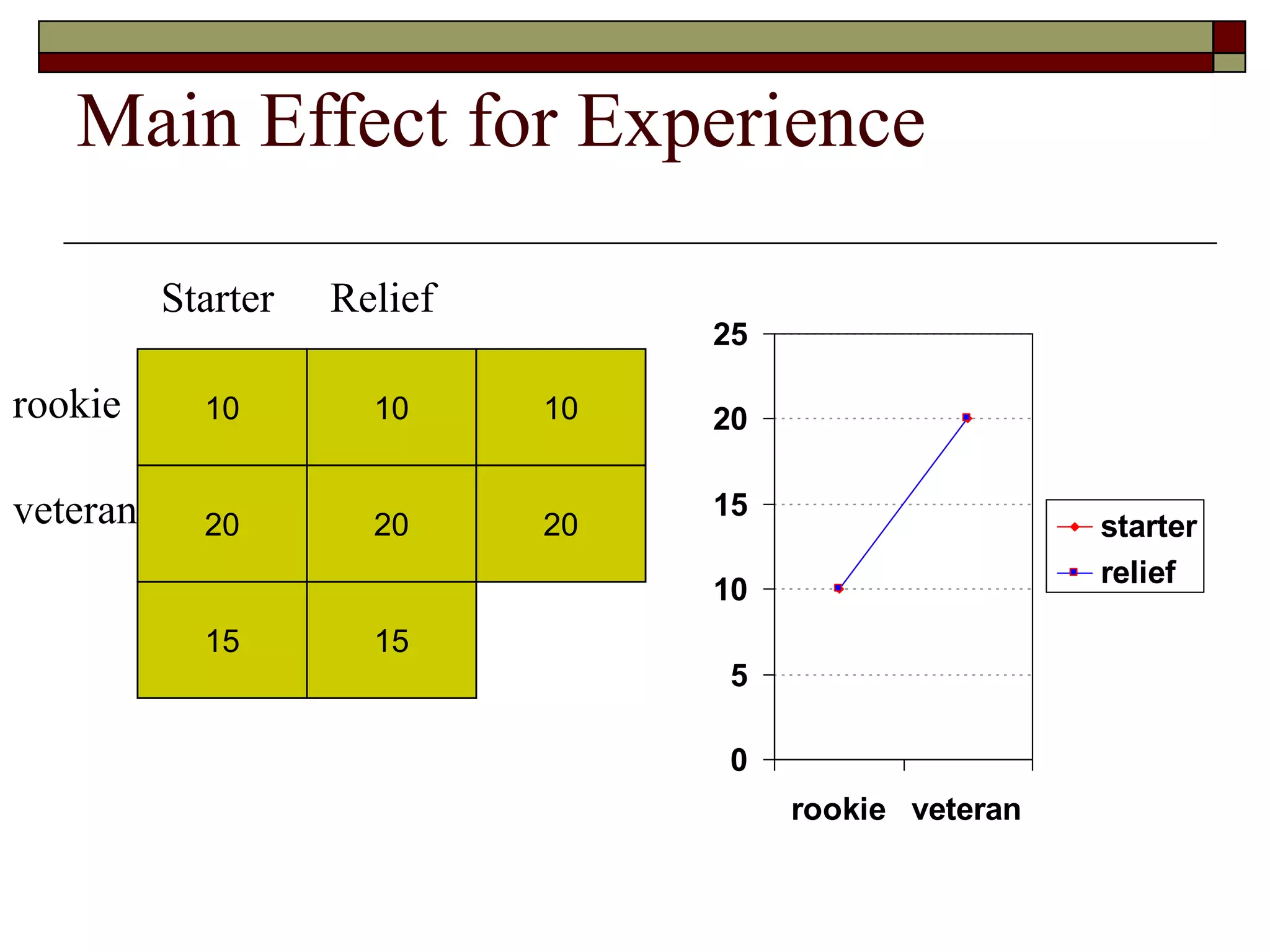
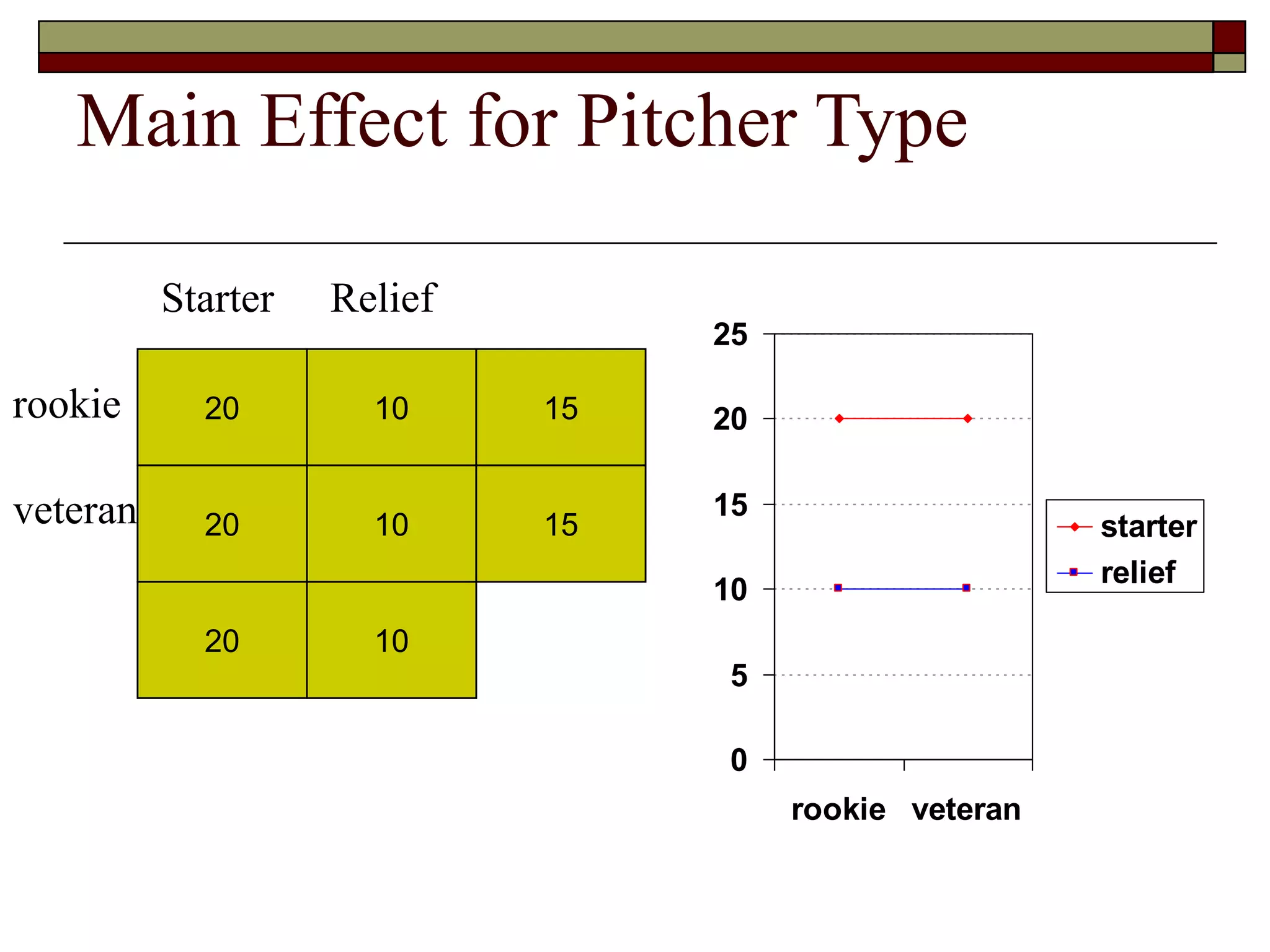
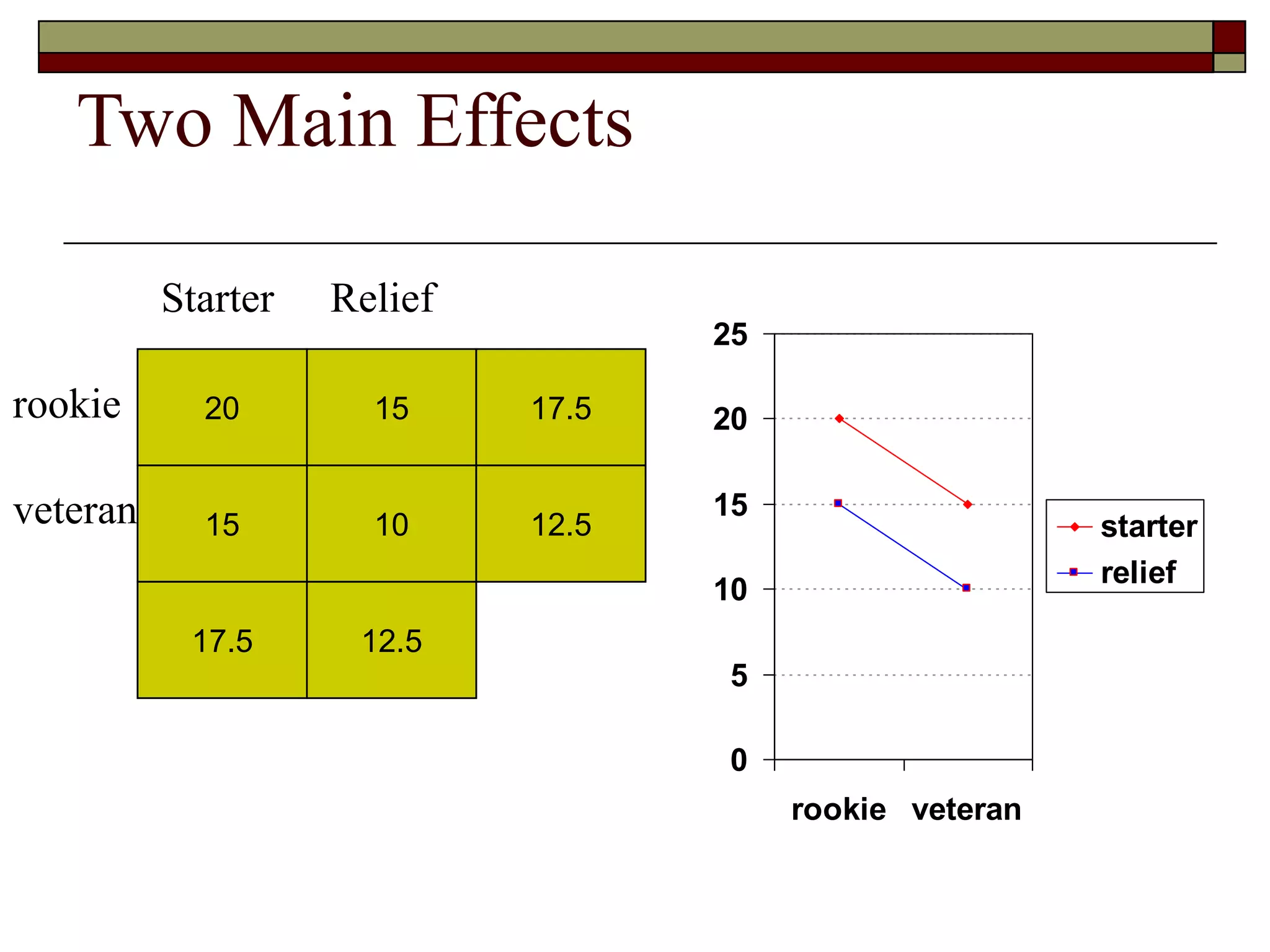
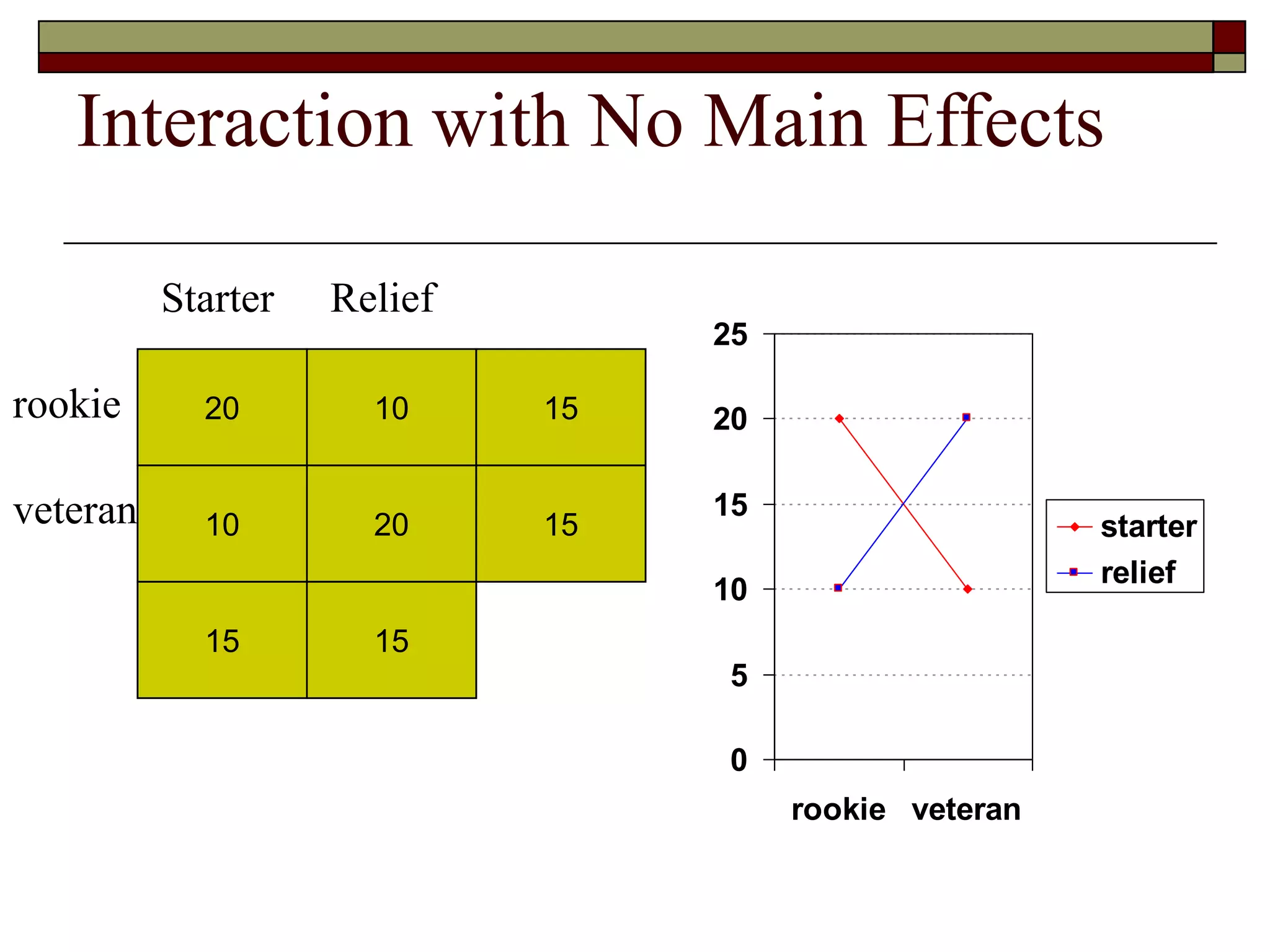
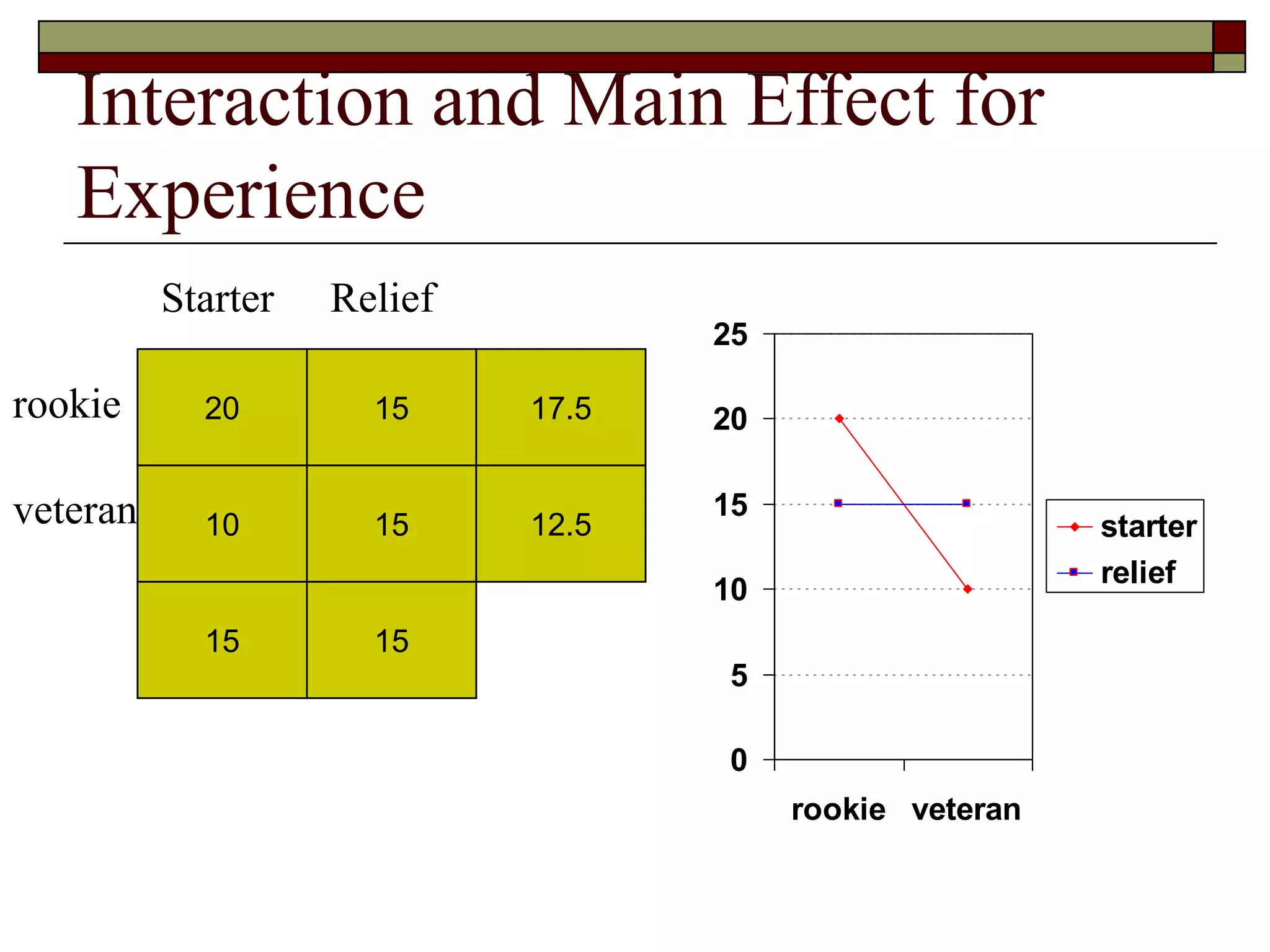
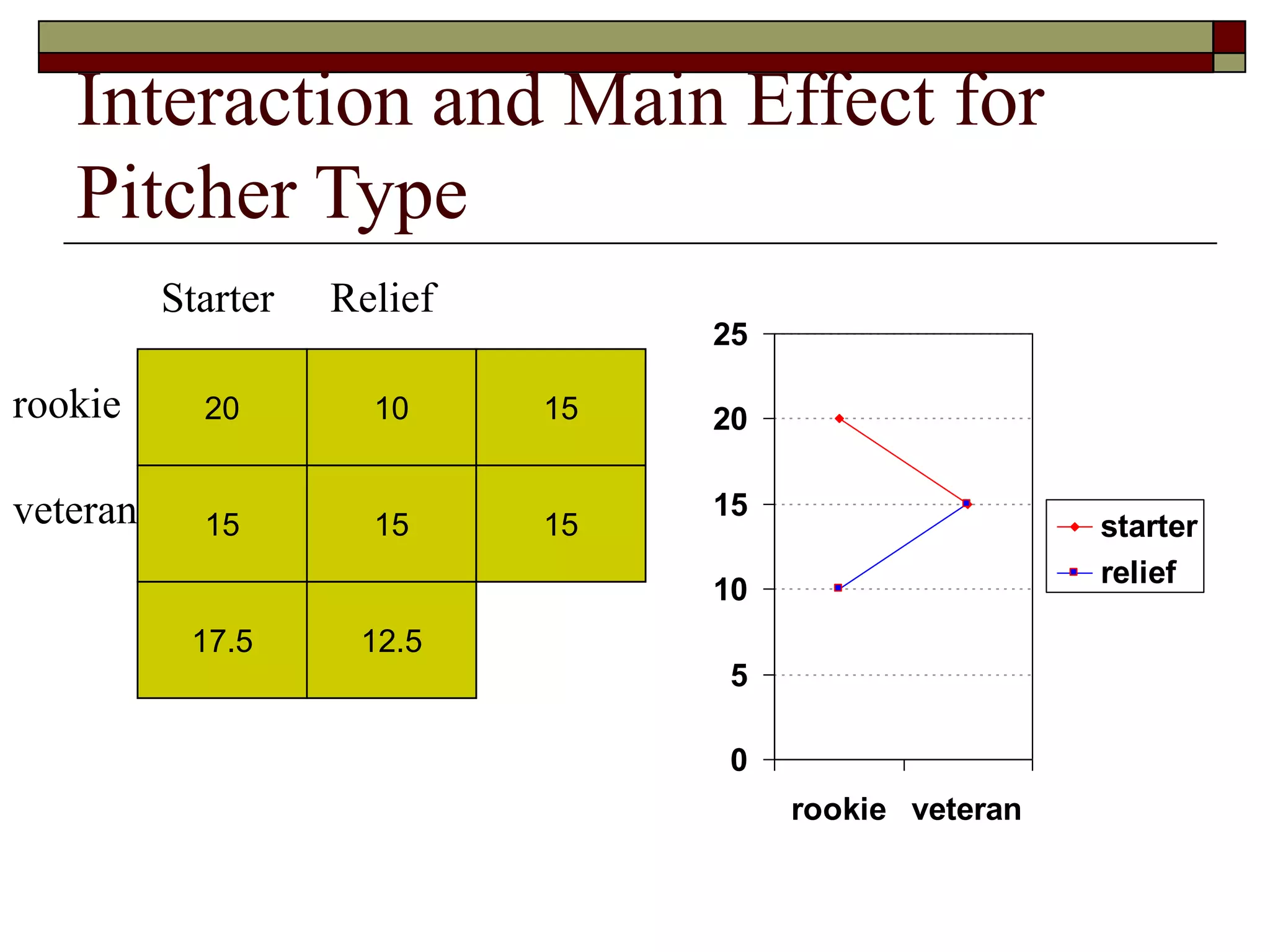
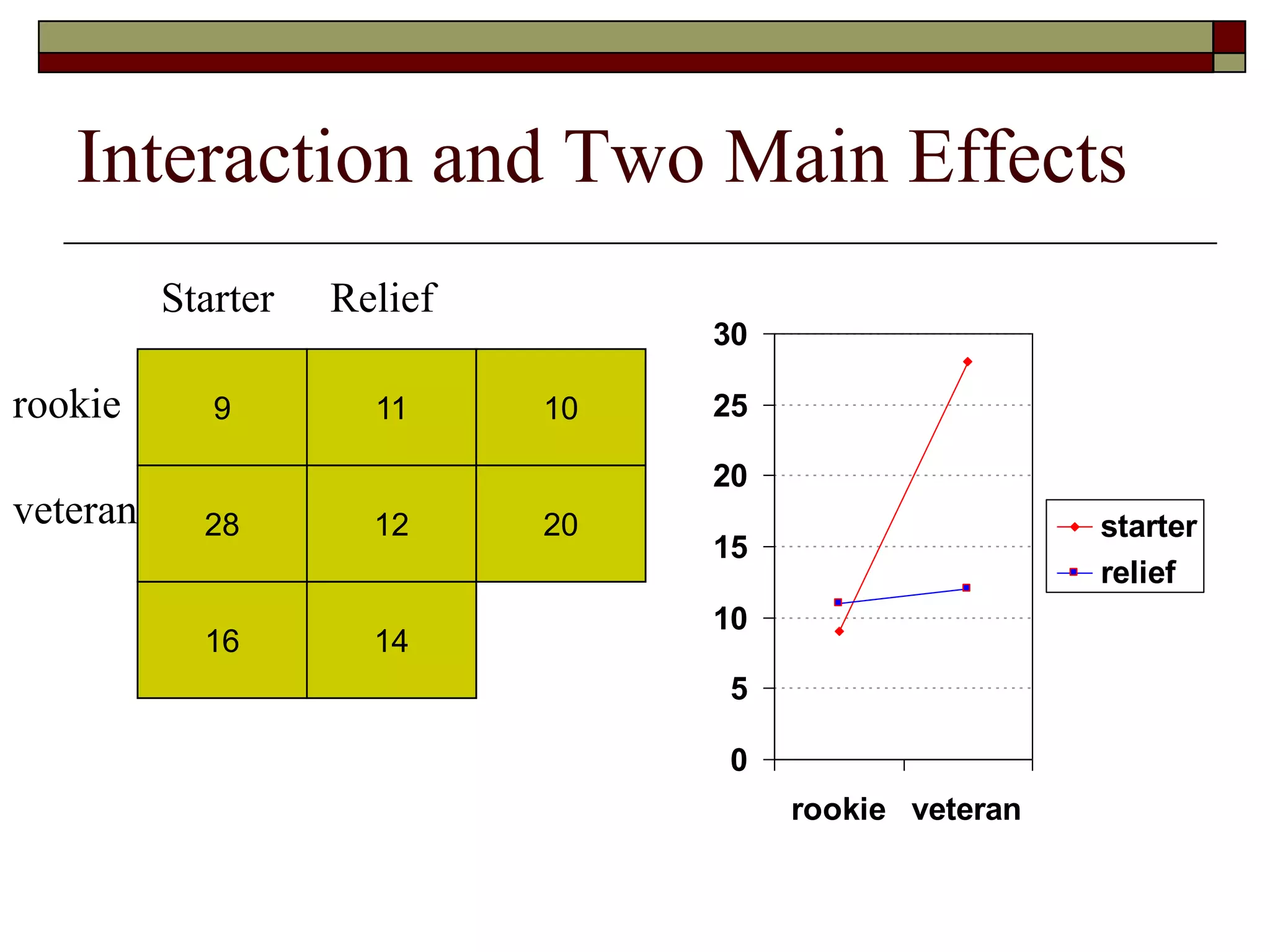
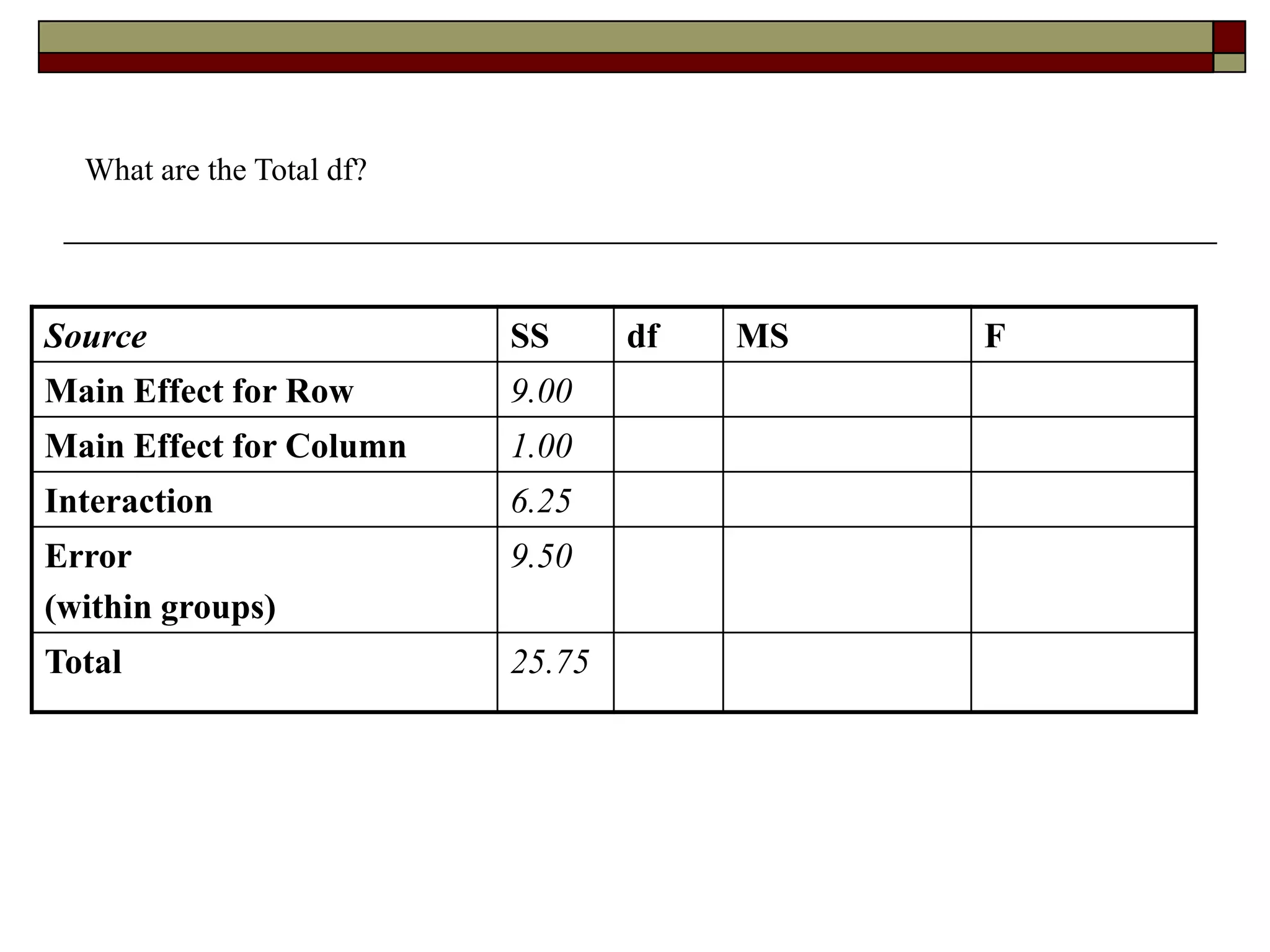
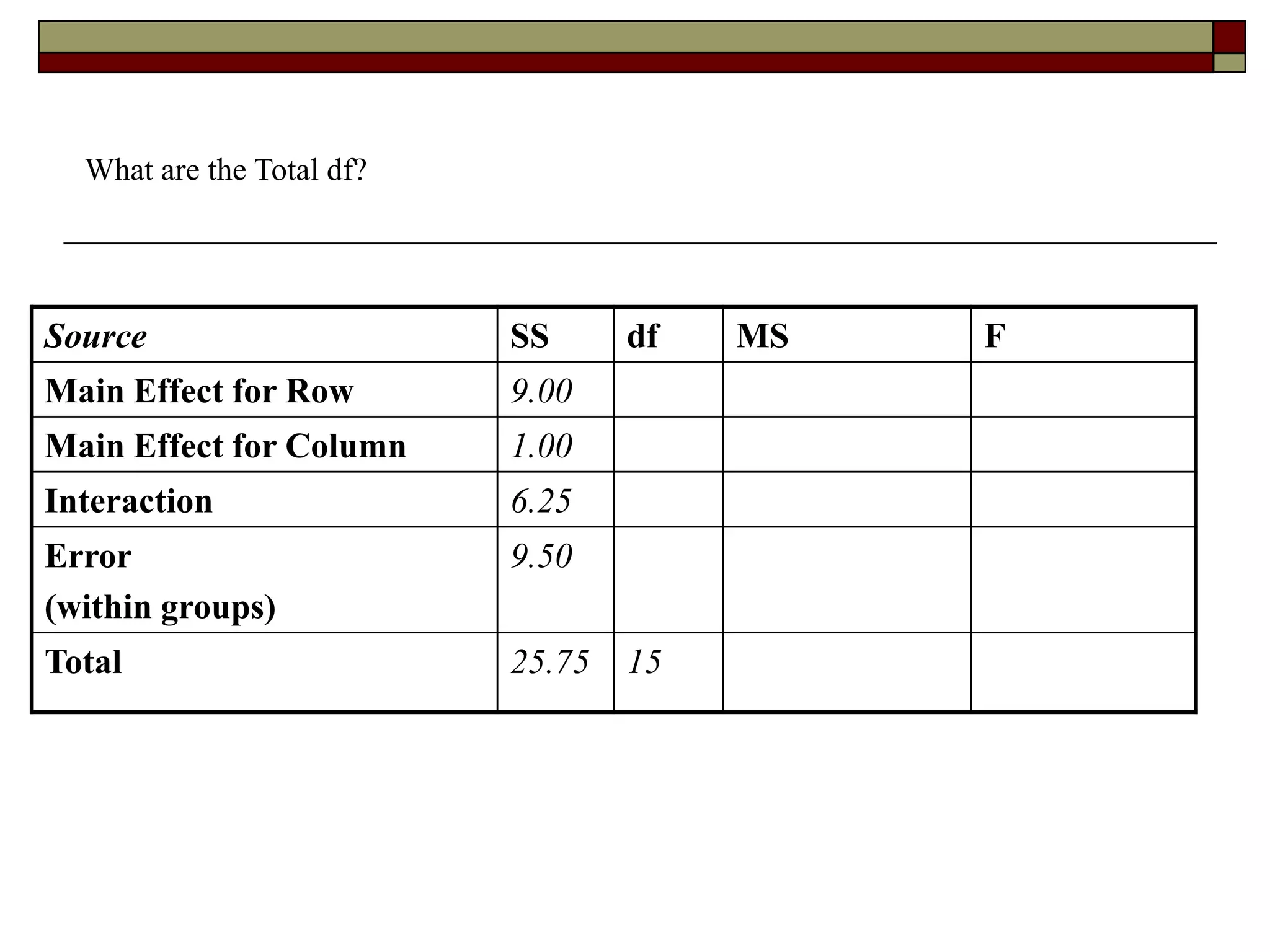
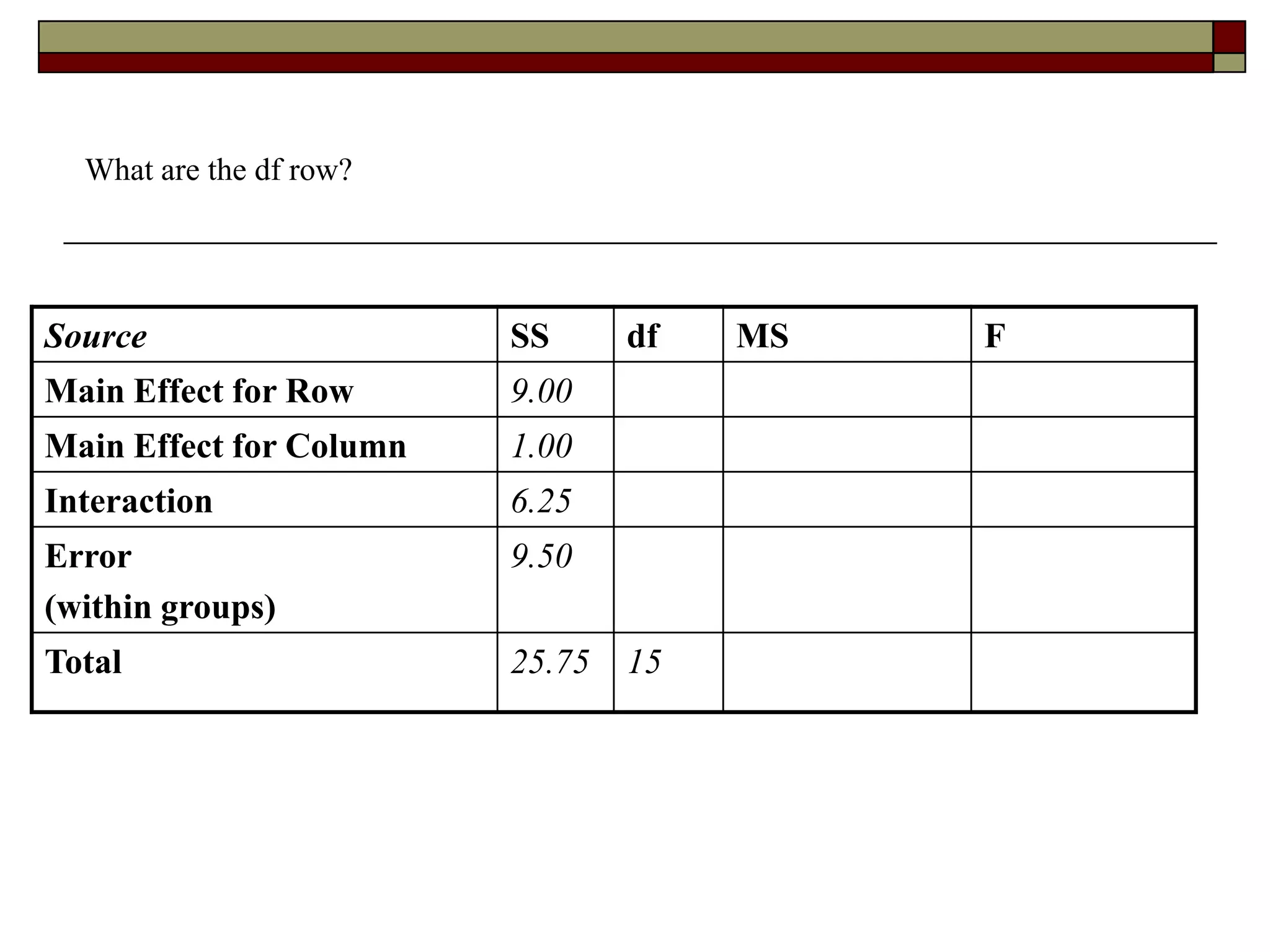
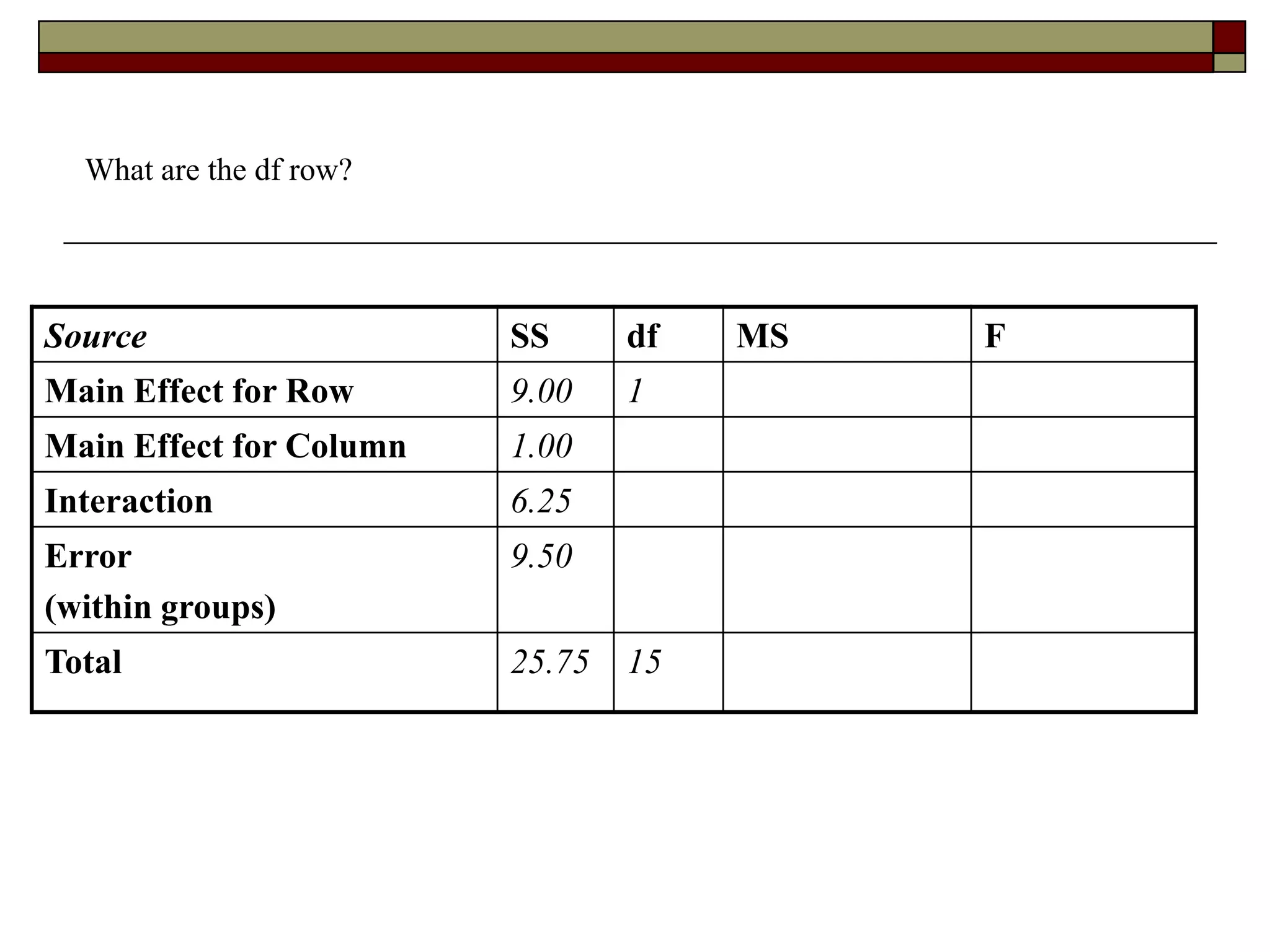
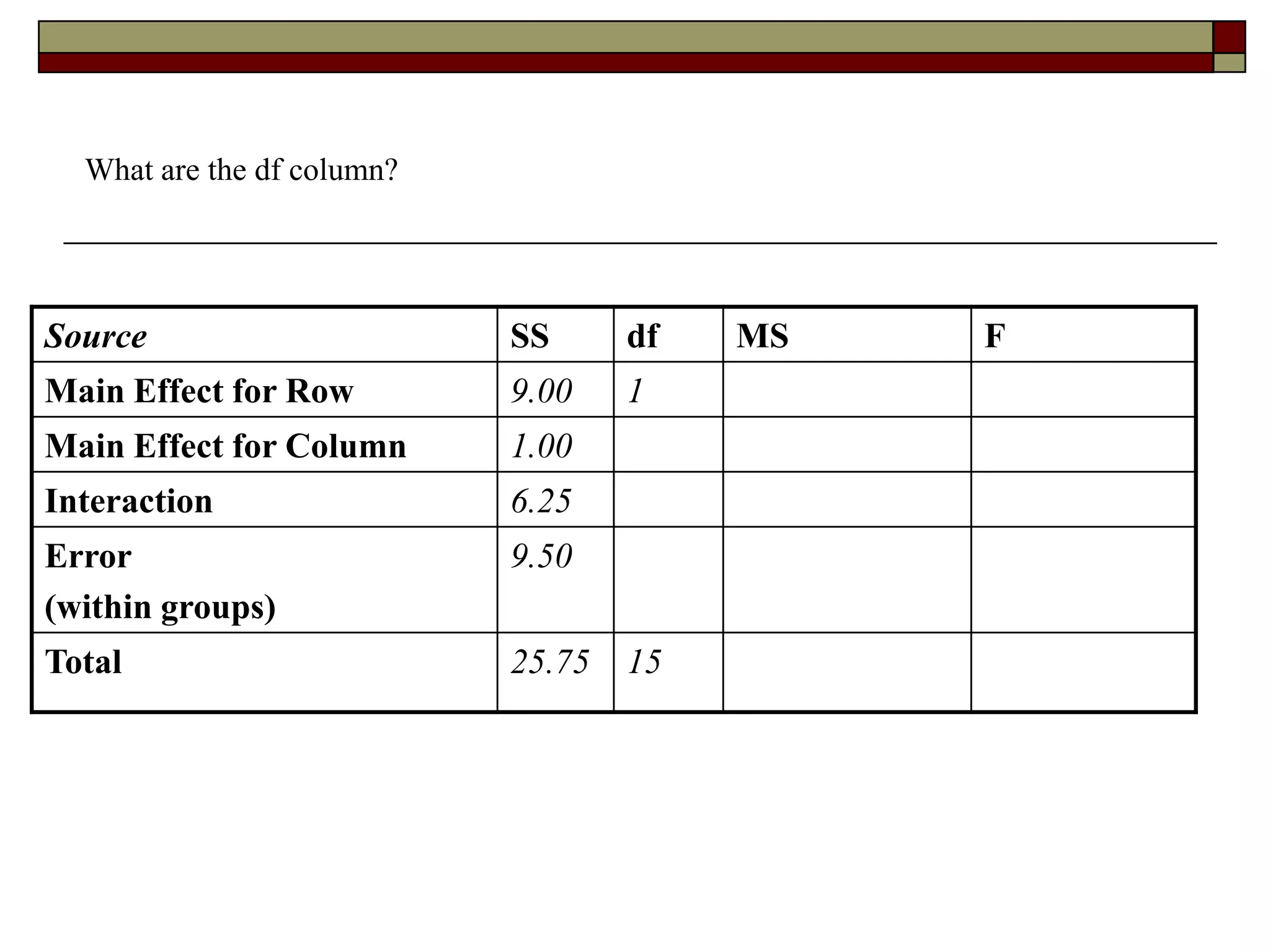
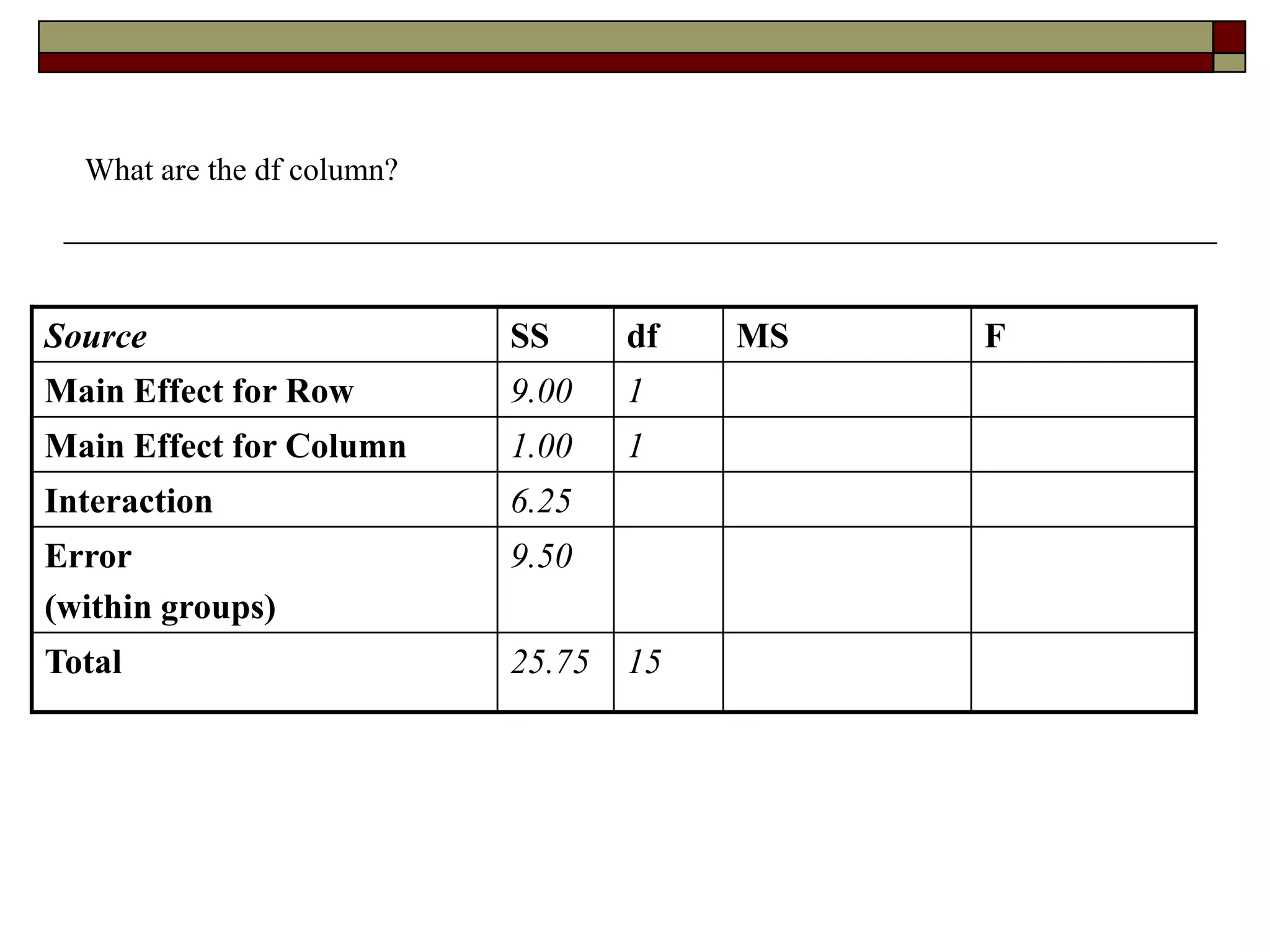
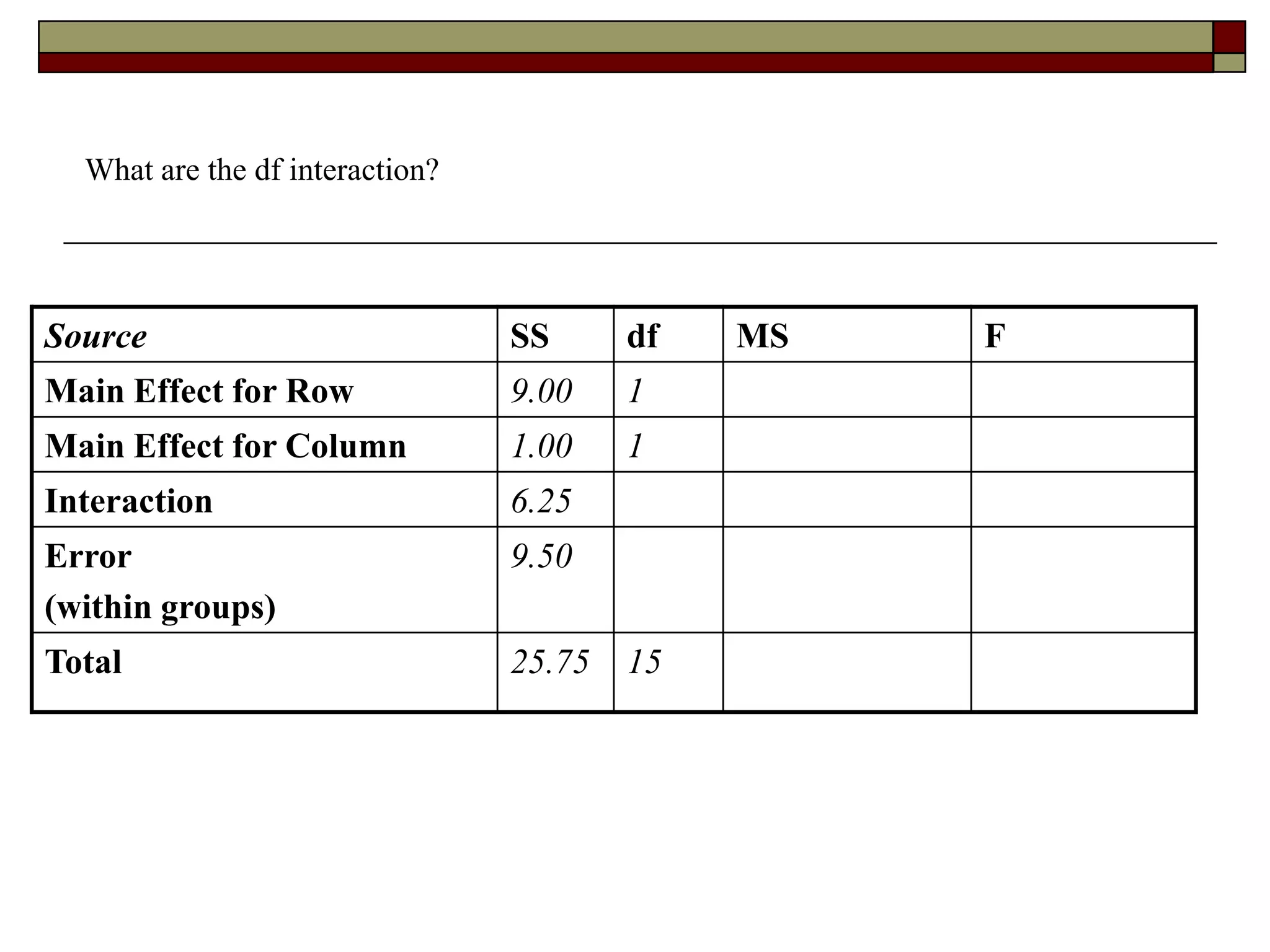
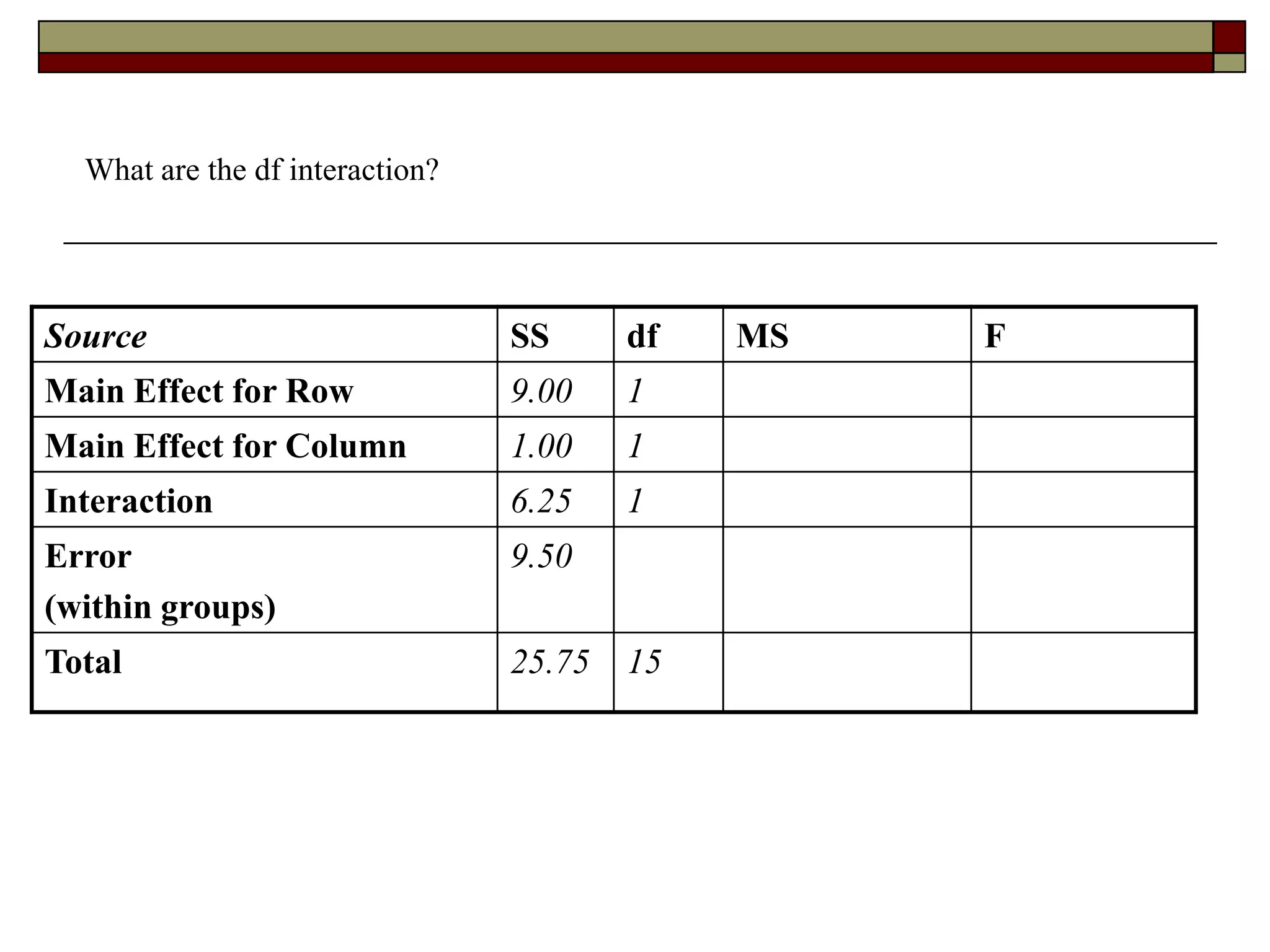
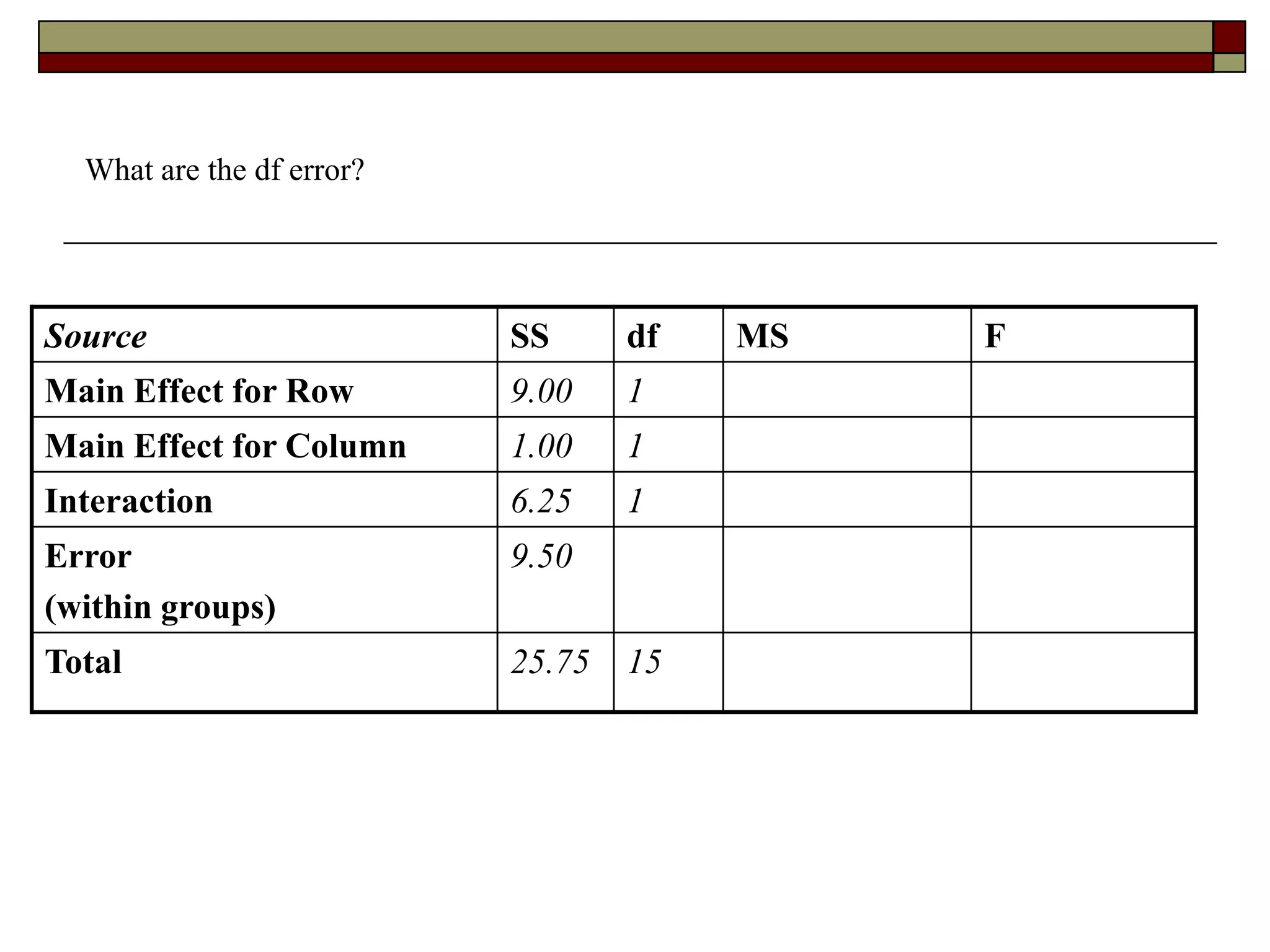
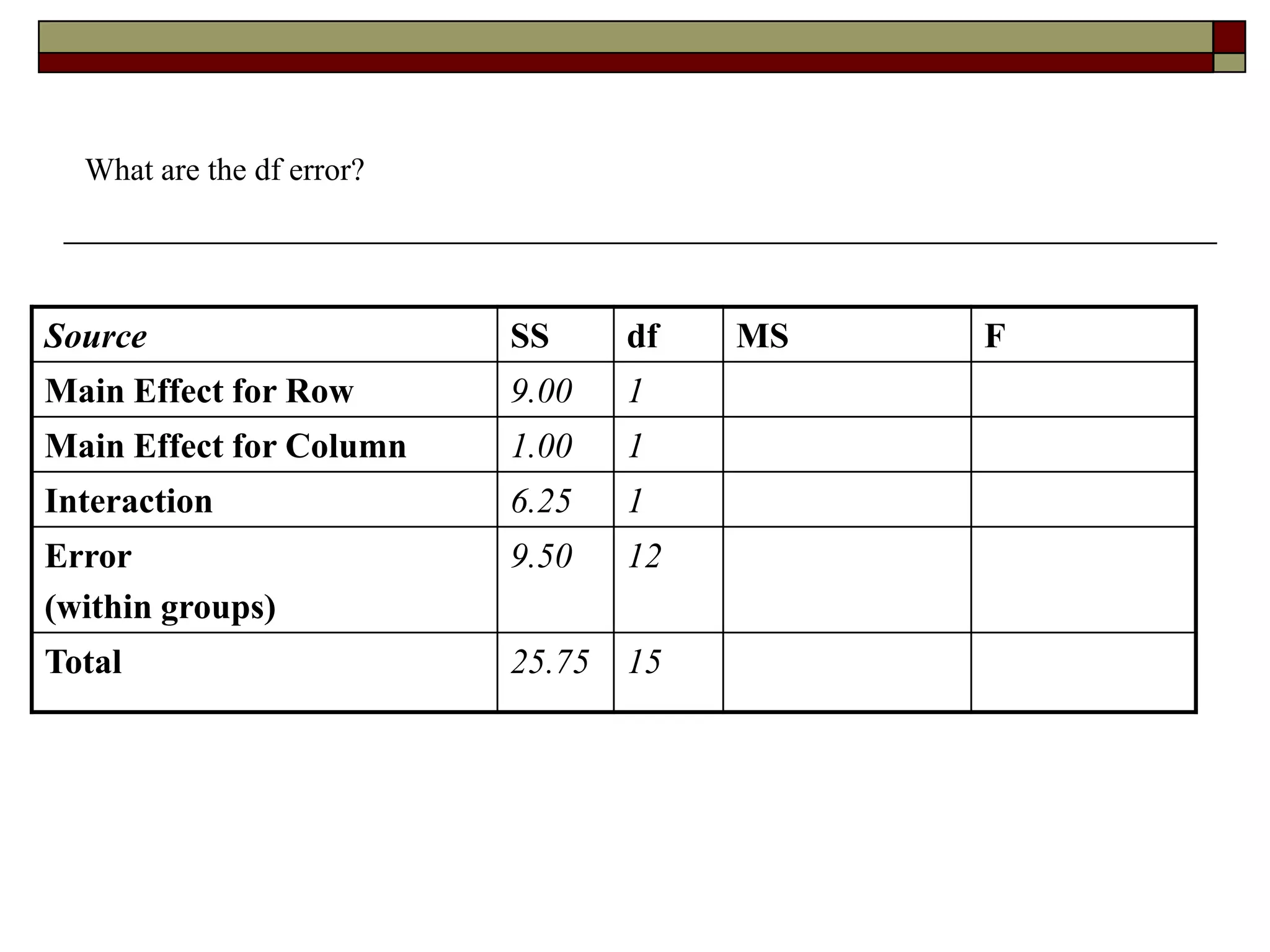
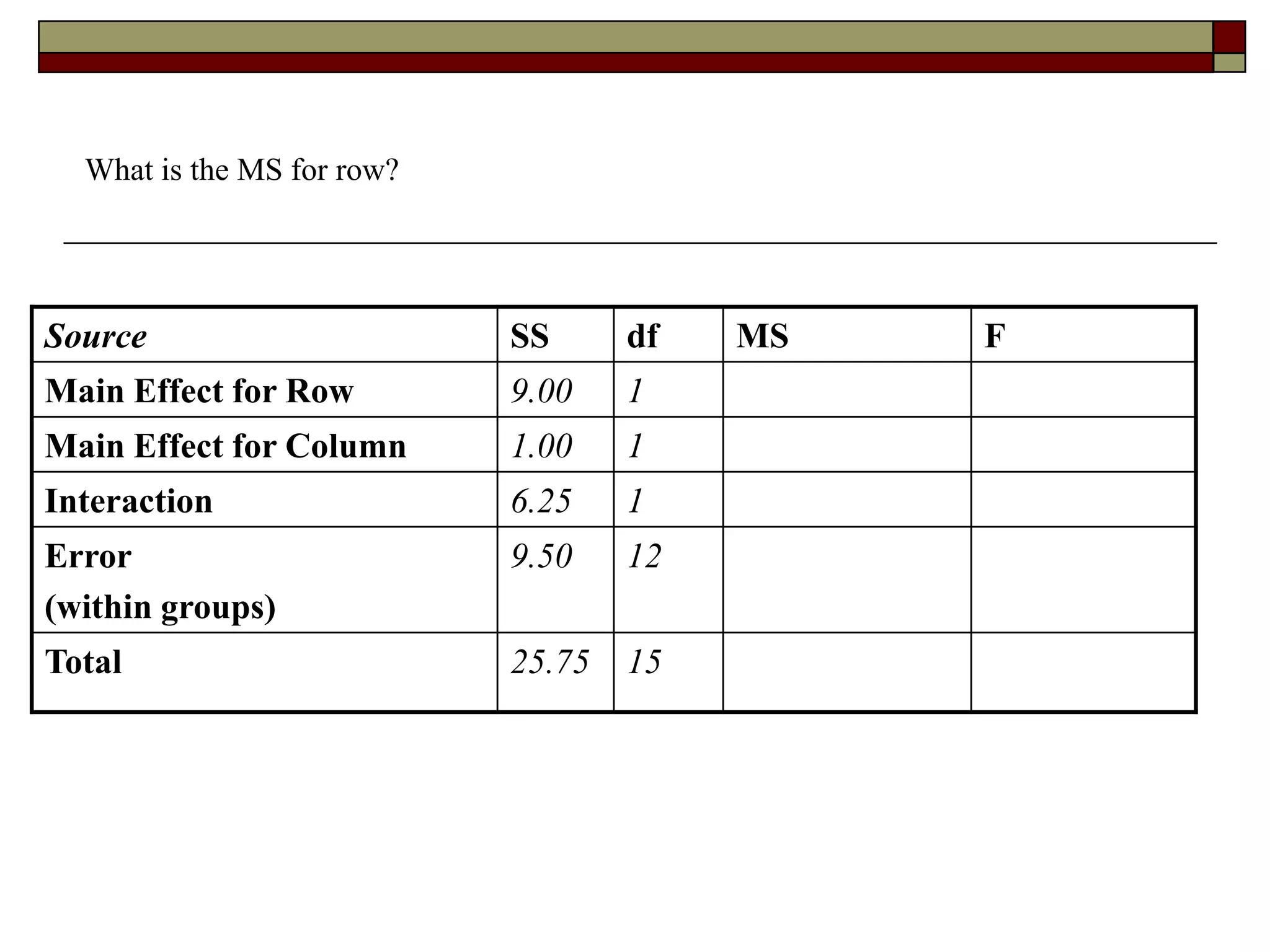
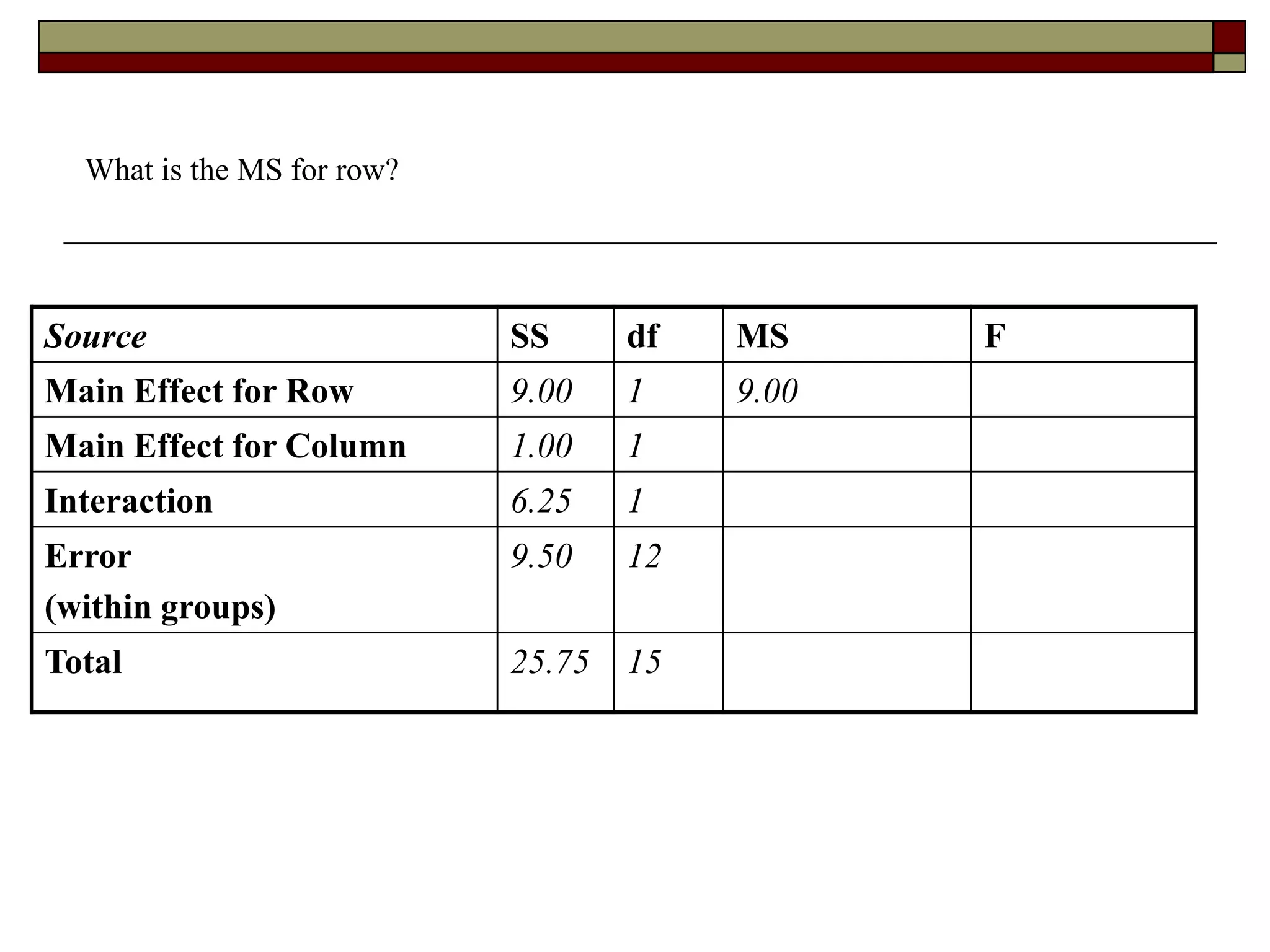
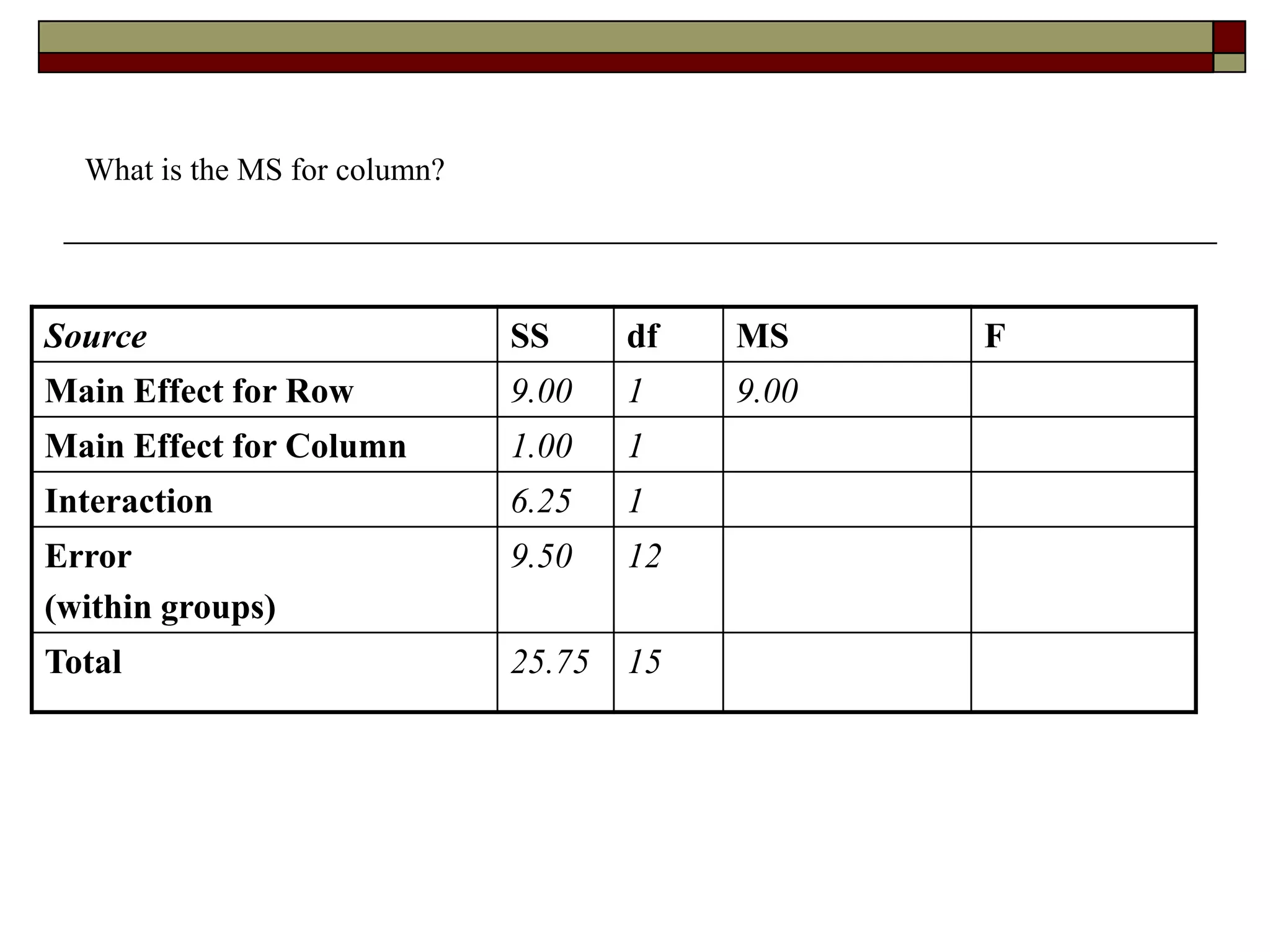
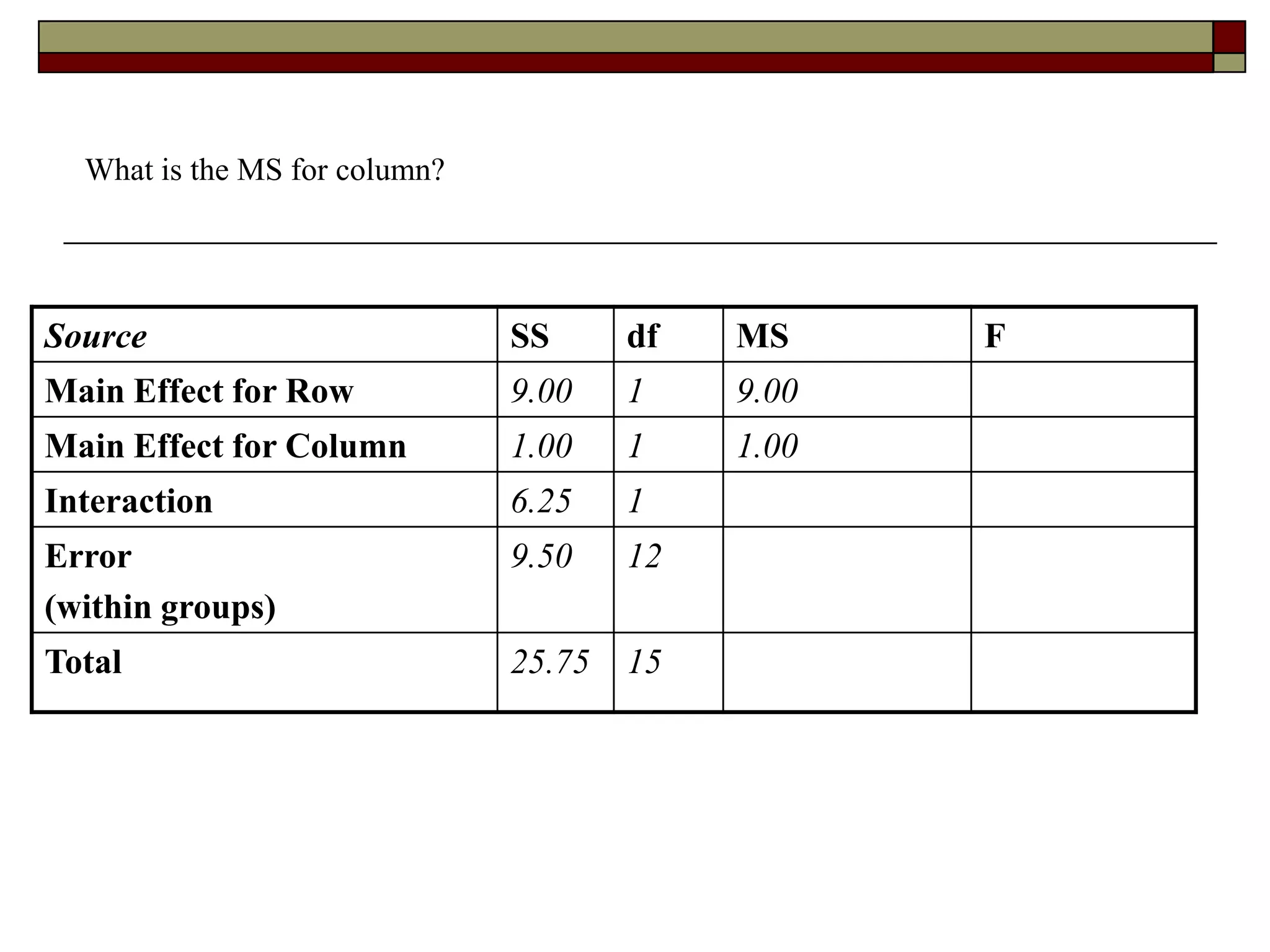
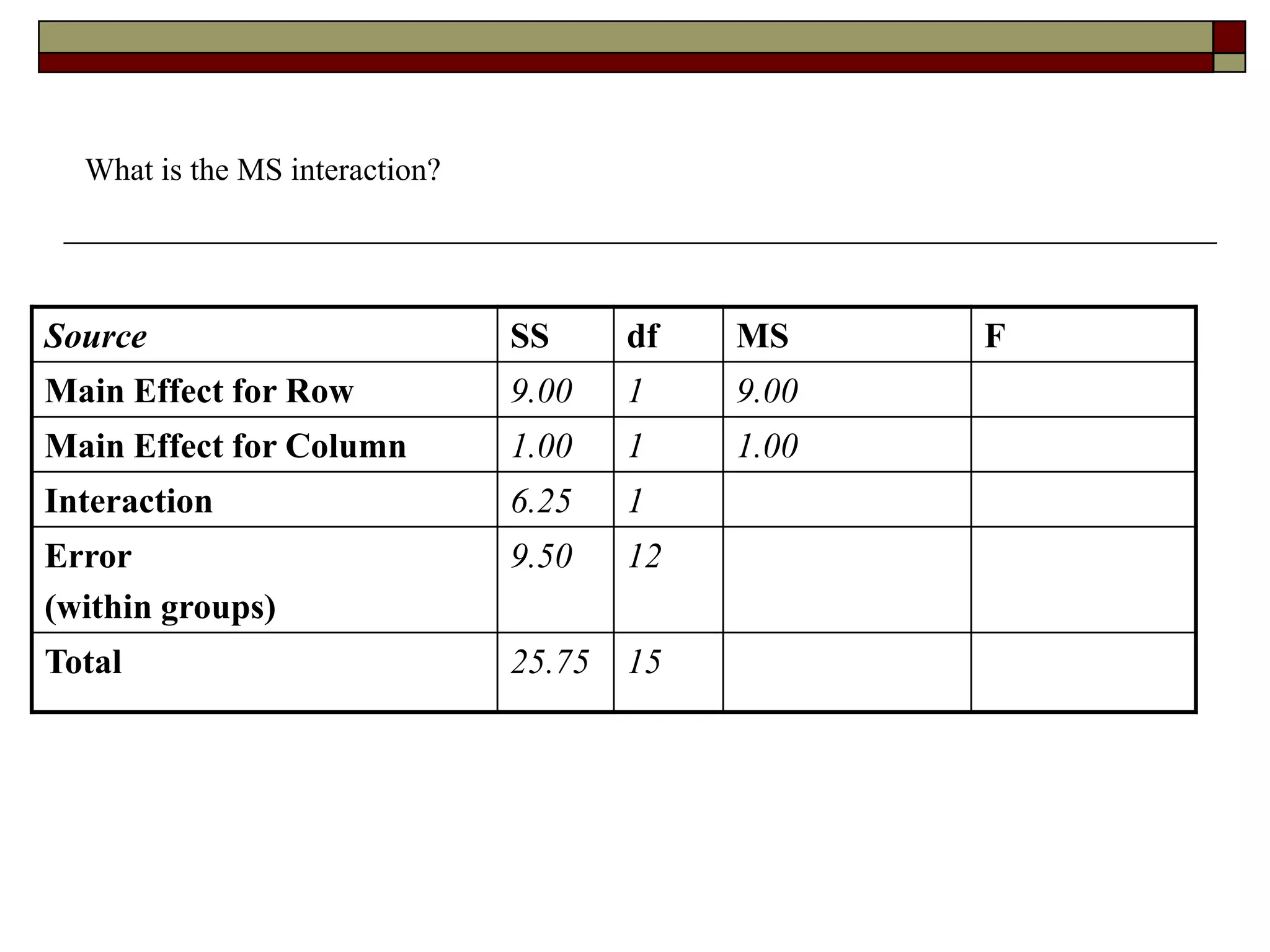
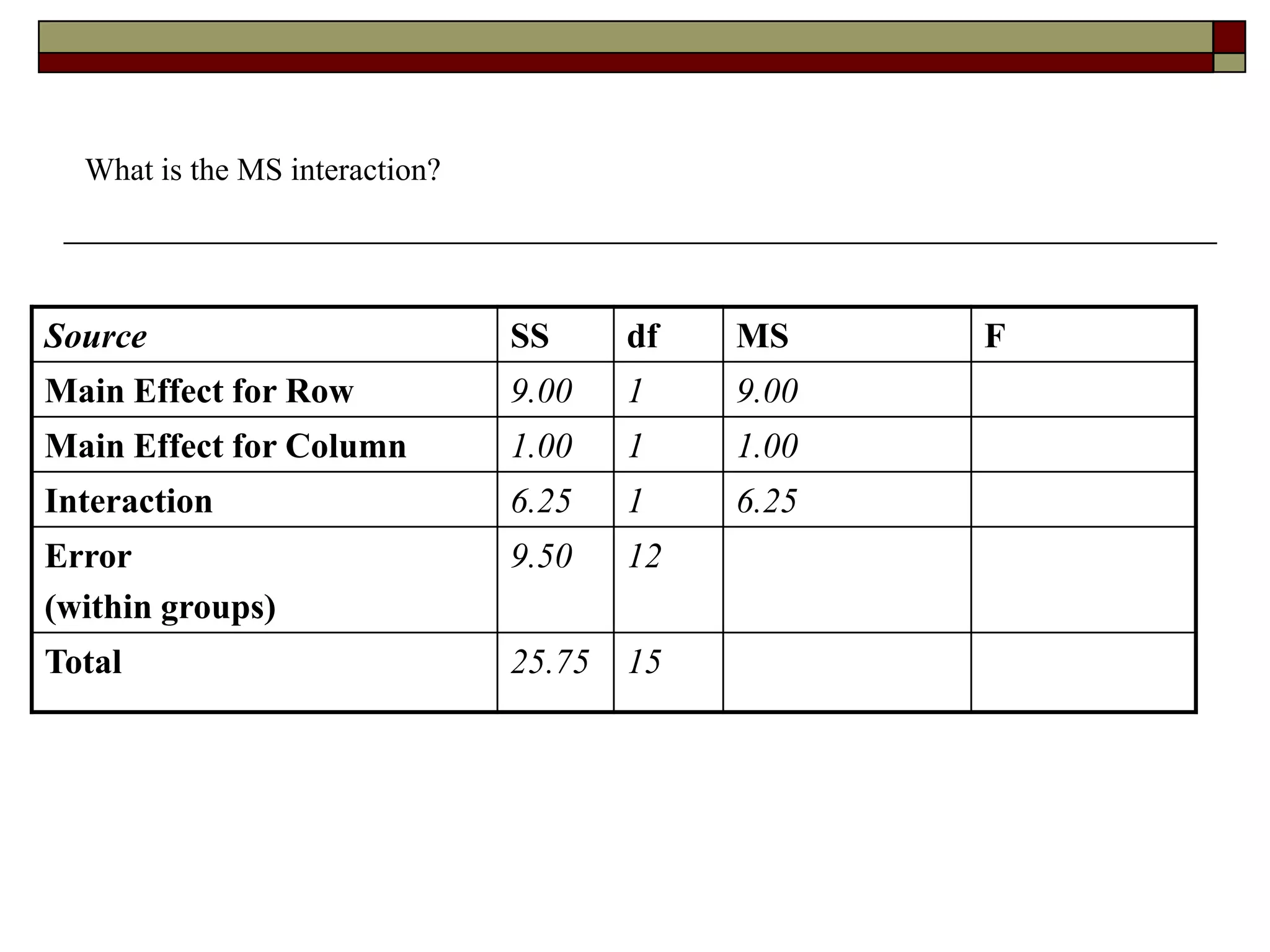
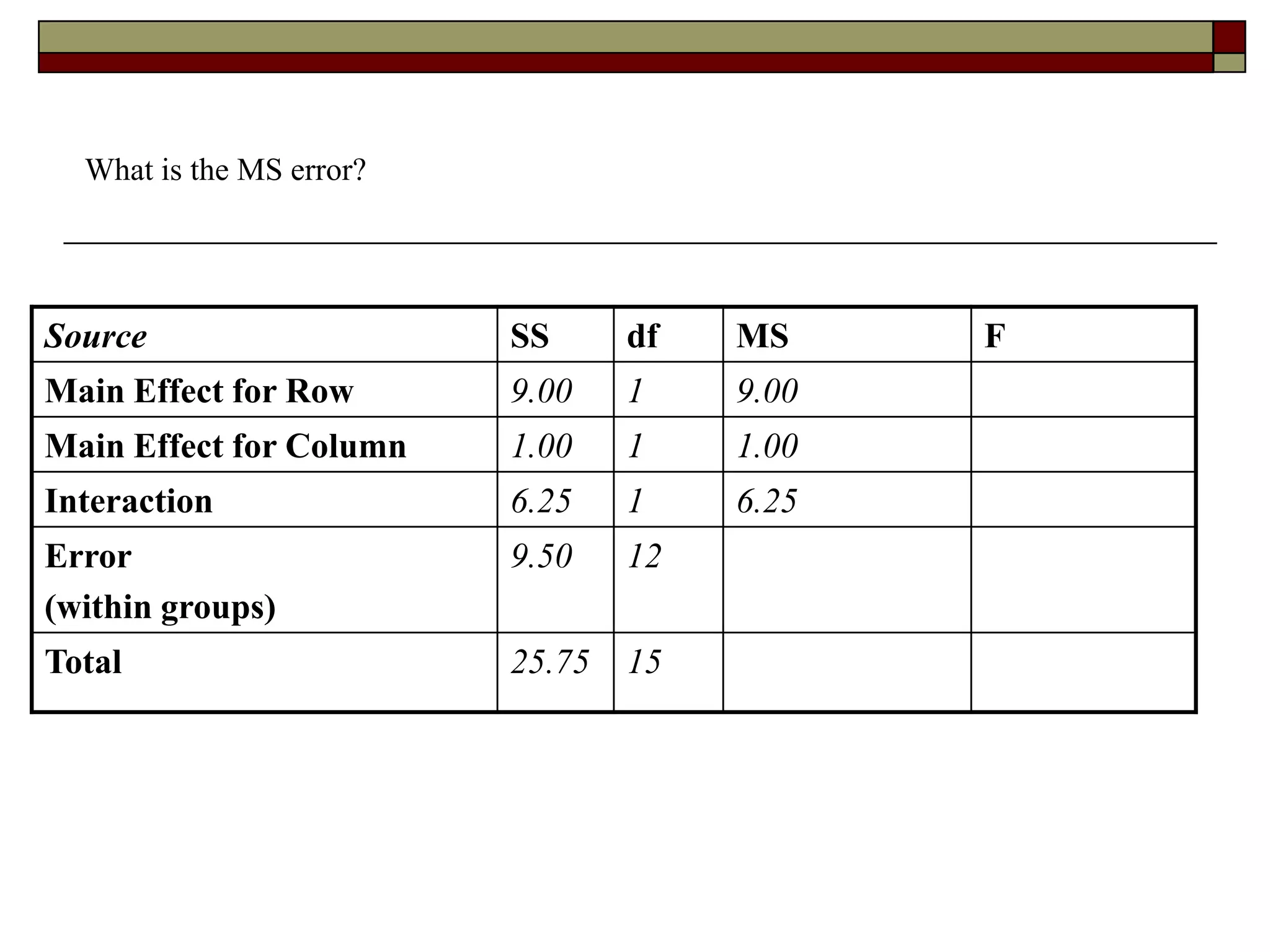
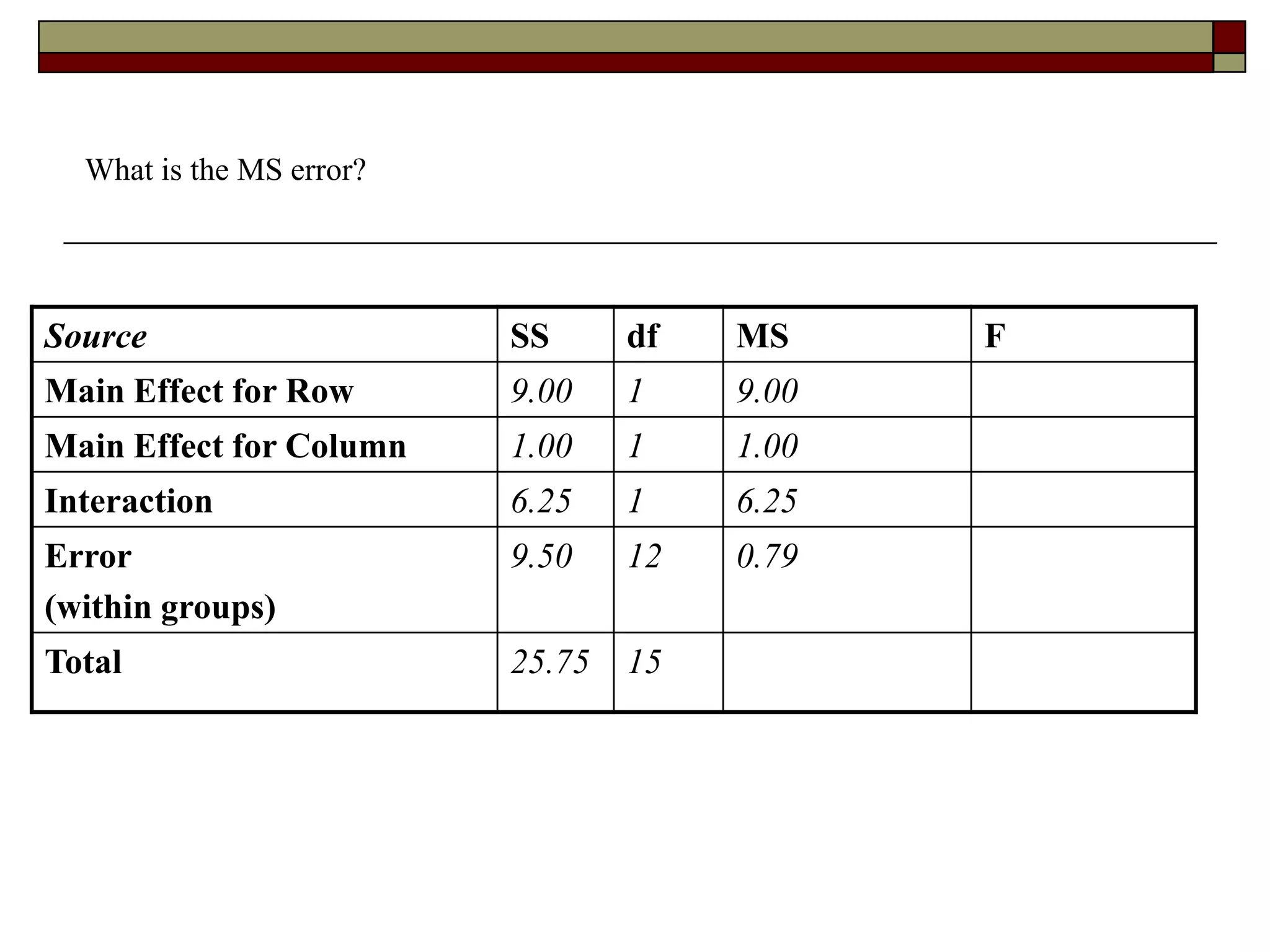
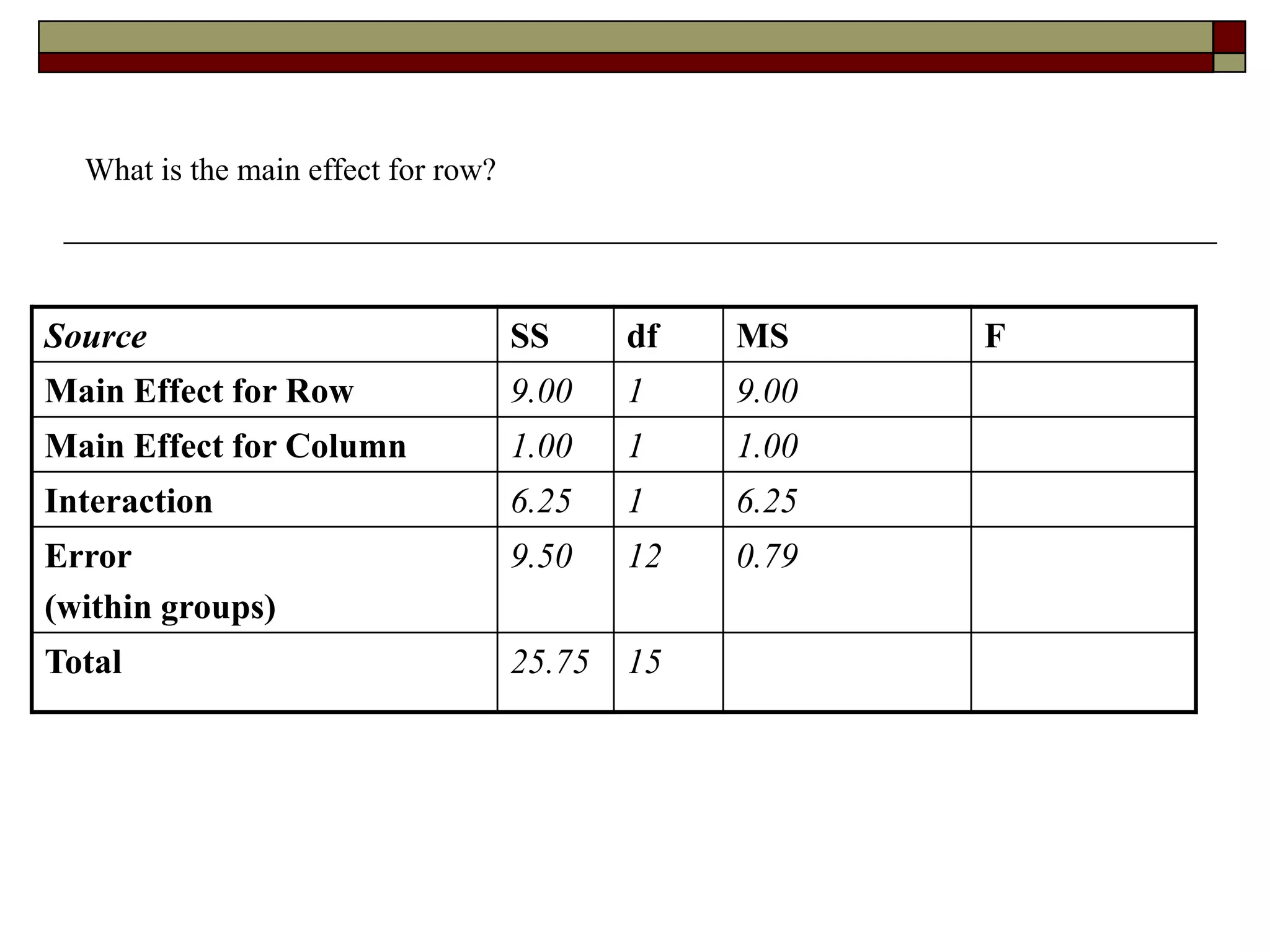
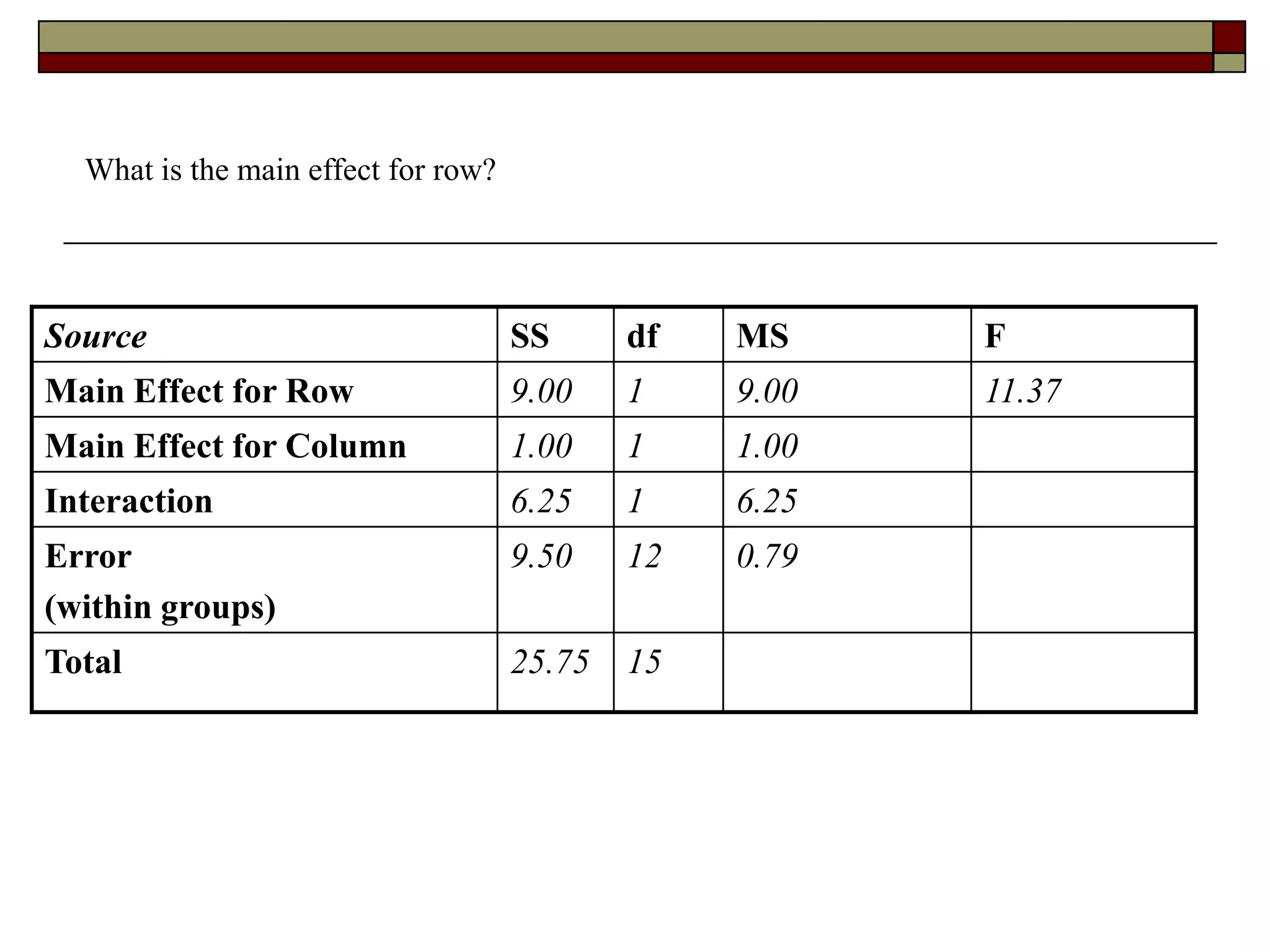
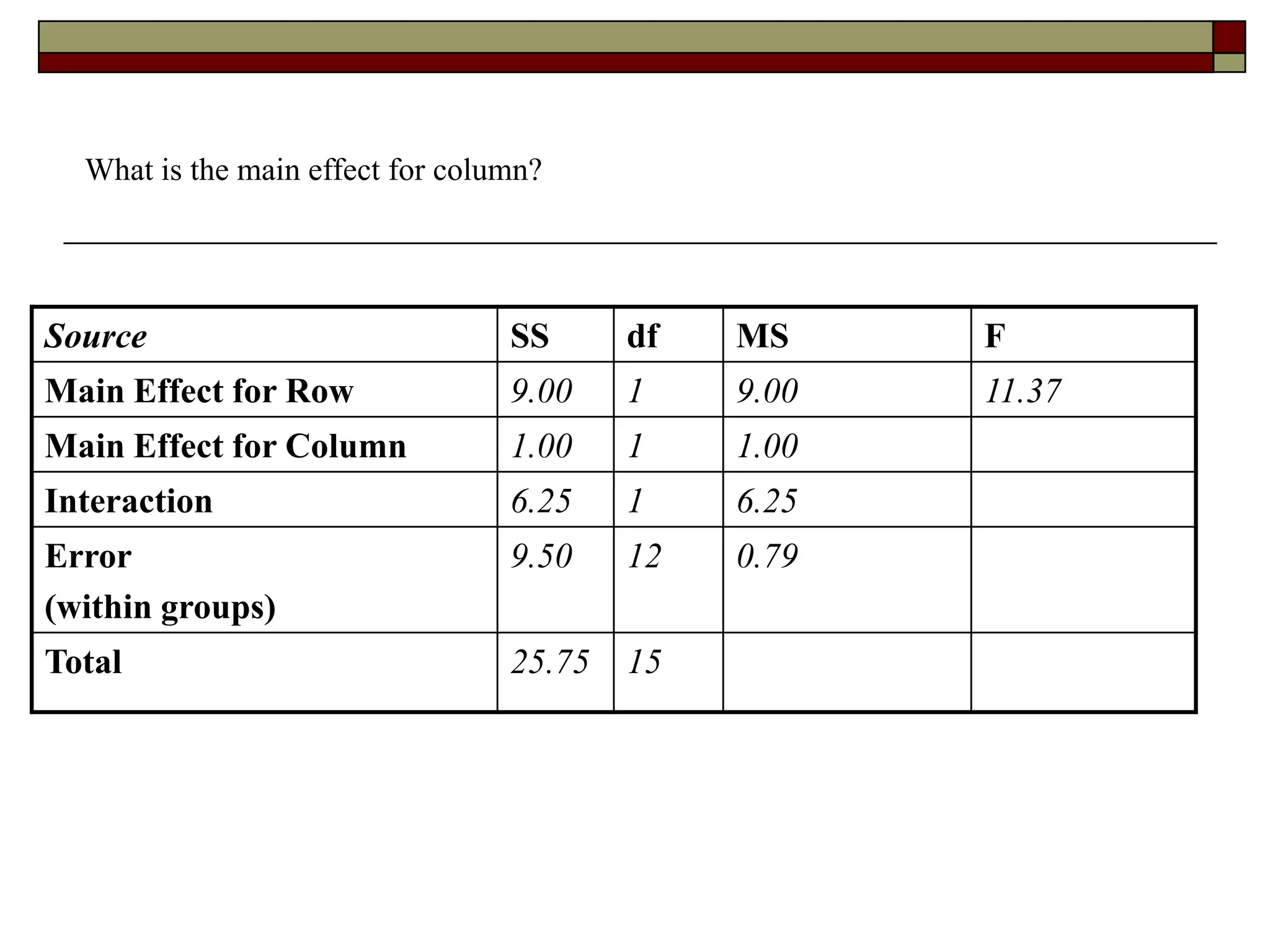
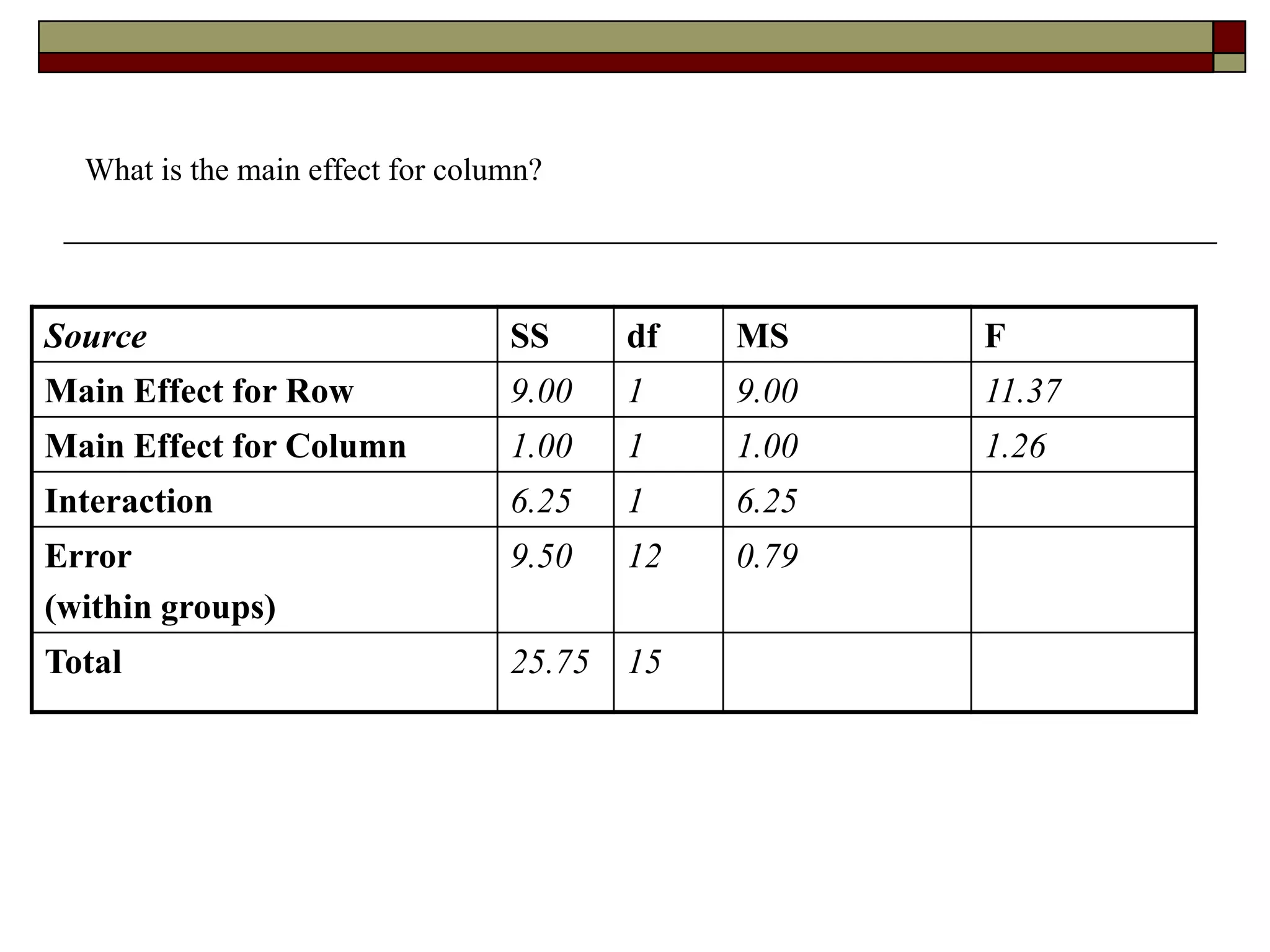
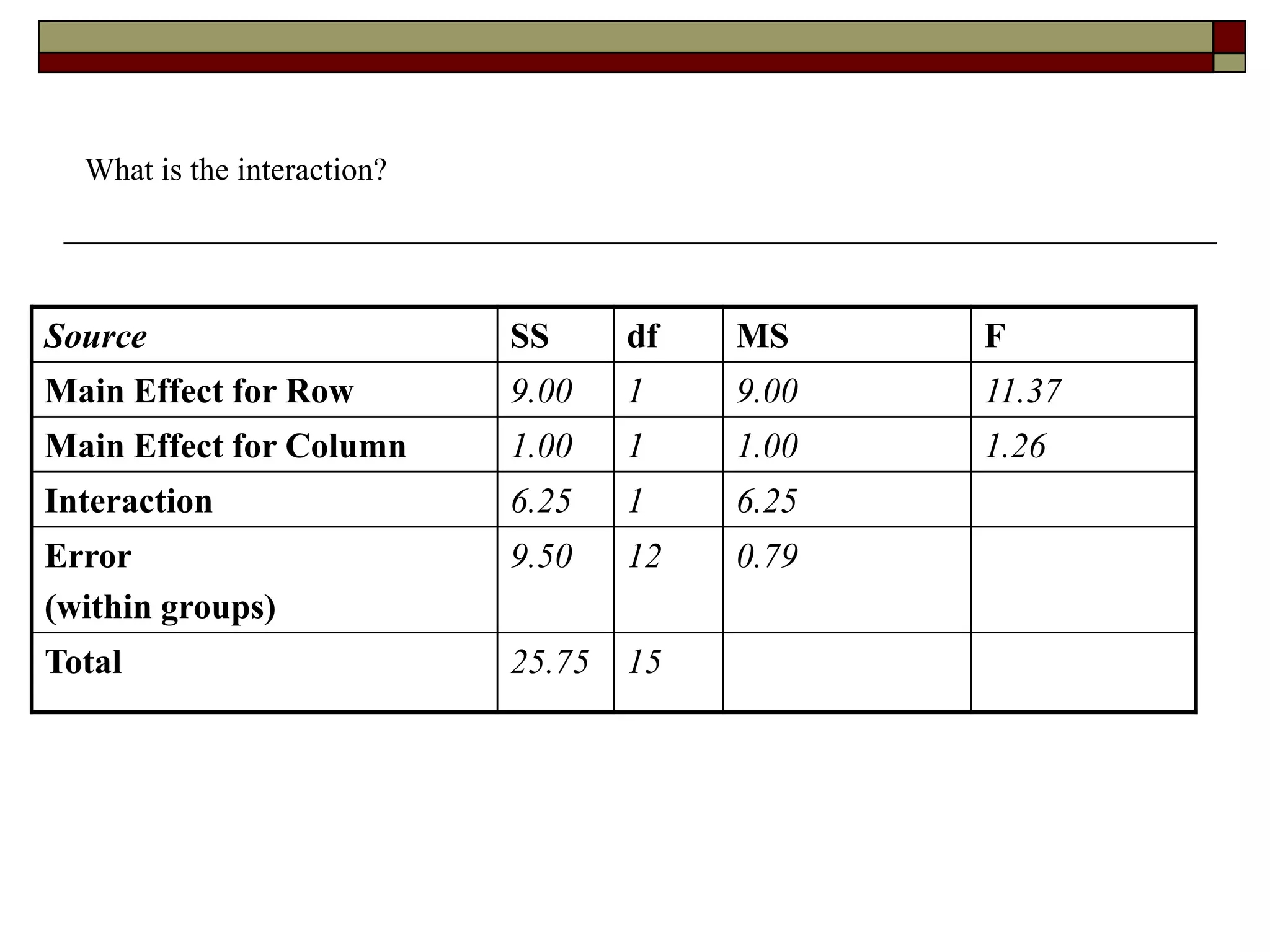
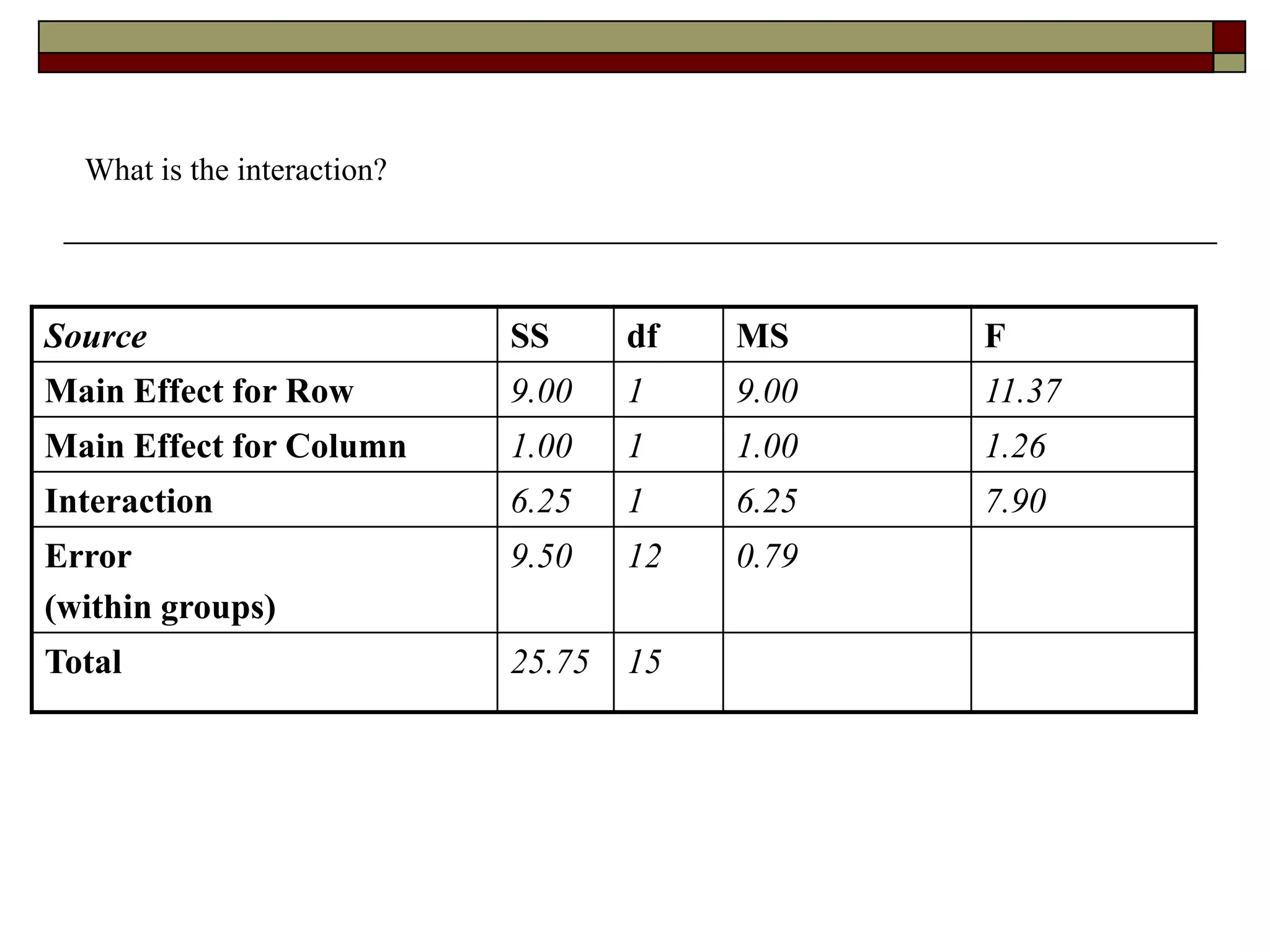
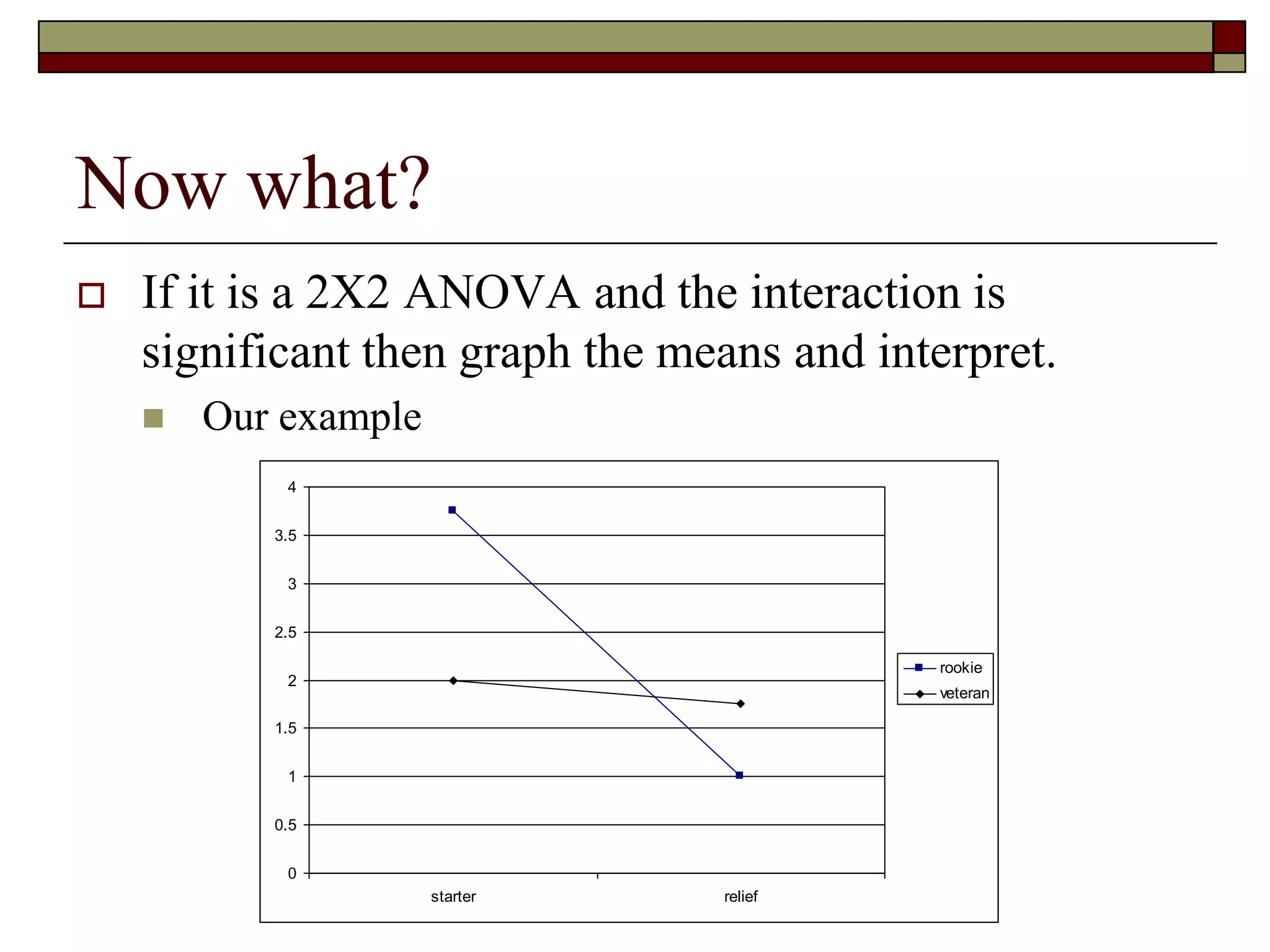
This document provides an overview of two-way between-subjects ANOVA. It describes two-way ANOVA as having two or more independent variables that are between-subjects factors. Main effects and interactions are computed. Main effects examine the effect of each independent variable collapsed across the other variable. Interactions occur when the effect of one variable depends on the level of the other variable. Examples of different patterns in data that could indicate main effects and interactions are presented in tables and graphs.

1. Two-way Between-
Subjects ANOVA

2. Two-way ANOVA
 Two-way ANOVA is one type of Factorial
ANOVA.
 Factorial ANOVAs are designs with two or
more between-subjects independent variables
 If there are within-subjects IVs, then they are
often called Mixed ANOVAs

3. Two-way ANOVA
 Grouping factors (IVs)
 Example
 IV: experience with three levels - rookie, novice, and veteran
 IV: pitcher type with two levels - starter and relief
 DV: physical stamina
 3 X 2 factorial design
 Computes a separate F ratio for each independent variable
(called main effects) and the interaction between the variables
 F for experience
 F for pitcher type
 F for experience*pitch interaction

4. Example: 3 X 2 Factorial Design
Group 1 Group 2
Group 3 Group 4
Starter Relief
Group 5 Group 6
rookie
novice
veteran
Experience
Level
Pitcher Type

5. Practice
 A 3 X 3 design
 How many independent variables?
1. 1
2. 2
3. 3
4. 4

6. Practice
 A 3 X 3 design
 How many levels of the first independent
variable listed?
1. 1
2. 2
3. 3
4. 4

7. Practice
 A 3 X 3 design
 How many conditions?
1. 2
2. 3
3. 6
4. 9

8. Practice
 A researcher tests male and female doctors
for manual dexterity . She tests dexterity for
different tools: scalpel, scissors, scope, and
probe.
 How many independent variables?
1. 1
2. 2
3. 3
4. 4

9. Practice
 A researcher tests male and female doctors for
manual dexterity . She tests dexterity for different
tools: scalpel, scissors, scope, and probe.
 How many levels of the second independent variable
(tools)?
1. 1
2. 2
3. 3
4. 4

10. Practice
 A researcher tests male and female doctors
for manual dexterity . She tests dexterity for
different tools: scalpel, scissors, scope, and
probe.
 How many conditions?
1. 2
2. 4
3. 6
4. 8

11. Practice
 You are studying factors that are associated with problem-
solving skills. You place subjects into groups according to the
following: student involvement with extracurricular activities
(involved vs. not involved), student university type (public
vs. private), and student self-reported procrastination (high,
medium, and low). You then test the students’ problem-
solving ability with a test.
 What is the design?
1. 1 X 2 X 2 X 3
2. 2 X 2 X 3
3. 3 X 2 X 6
4. 4 X 3

12. Practice
 You are studying factors that are associated with problem-
solving skills. You place subjects into groups according to the
following: student involvement with extracurricular activities
(involved vs. not involved), student university type (public
vs. private), and student self-reported procrastination (high,
medium, and low). You then test the students’ problem-
solving ability with a test.
 How many independent variables?
1. 1
2. 2
3. 3
4. 4

13. Practice
 You are studying factors that are associated with problem-
solving skills. You place subjects into groups according to the
following: student involvement with extracurricular activities
(involved vs. not involved), student university type (public
vs. private), and student self-reported procrastination (high,
medium, and low). You then test the students’ problem-
solving ability with a test.
 How many cells?
1. 3
2. 8
3. 12
4. 24

14. Two-way ANOVA
 Main Effects
 Think of them as one-way ANOVAs for each
independent variable.
 If you have 2 IVs, then you have two possible
main effects
 Example
 A main effect for experience would look at the
three levels ignoring (collapsed across) pitcher type
 A main effect for pitcher type looks at starters vs.
relief pitchers regardless of (collapsed across)
experience

15. Group 1 Group 2
Group 3 Group 4
Starter Relief
Group 5 Group 6
rookie
novice
veteran
Experience
Level
Pitcher Type
Marginal Mean
For Rookie
Marginal Mean
For Novice
Marginal Mean
For Veteran
Marginal Mean
For Starter
Marginal Mean
For Relief

16. Two-way ANOVA
 Interaction
 For a two-way ANOVA there is one possible interaction
 Interactions occur if the effects of one IV are different
under different levels of the other IV
 Example
 Something about being an expert makes you behave differently if
you are a starter as opposed to being a relief pitcher.
 As the number of factors increases, the number of
possible interaction increases

17. Practice
 You are studying factors that are associated with problem-
solving skills. You place subjects into groups according to the
following: student involvement with extracurricular activities
(involved vs. not involved), student university type (public
vs. private), and student self-reported procrastination (high,
medium, and low). You then test the students’ problem-
solving ability with a test.
 How many main effects are possible?
1. 1
2. 2
3. 3
4. 4

18. Practice
 You are studying factors that are associated with problem-
solving skills. You place subjects into groups according to the
following: student involvement with extracurricular activities
(involved vs. not involved), student university type (public
vs. private), and student self-reported procrastination (high,
medium, and low). You then test the students’ problem-
solving ability with a test.
 How many interactions are possible?
1. 1
2. 2
3. 3
4. 4

19. Two-way ANOVA
 Identifying main effects and interactions
 First test for significance (will discuss how that is done
later)
 Then use either table or graph to see the relationship that
exists between variables
 For instructional purposes we will assume the tests for
significance have been done and that the main effects and
interactions identified are significant
 Remember if not significant than no exploration of that
particular main effect or interaction.

20. Group 1 Group 2
Group 3 Group 4
Starter Relief
rookie
veteranExperience
Level
Pitcher Type
Marginal Mean
For Rookie
Marginal Mean
For Veteran
Marginal Mean
For Starter
Marginal Mean
For Relief

21. No Main Effects or Interaction
20 20
Starter Relief
rookie
veteran
20
20 20 20
20 20
0
5
10
15
20
25
rookie veteran
starter
relief

22. Main Effect for Experience
10 10
Starter Relief
rookie
veteran
10
20 20 20
15 15
0
5
10
15
20
25
rookie veteran
starter
relief

23. Main Effect for Pitcher Type
20 10
Starter Relief
rookie
veteran
15
20 10 15
20 10
0
5
10
15
20
25
rookie veteran
starter
relief

24. Two Main Effects
20 15
Starter Relief
rookie
veteran
17.5
15 10 12.5
17.5 12.5
0
5
10
15
20
25
rookie veteran
starter
relief

25. Interaction with No Main Effects
20 10
Starter Relief
rookie
veteran
15
10 20 15
15 15
0
5
10
15
20
25
rookie veteran
starter
relief

26. Interaction and Main Effect for
Experience
20 15
Starter Relief
rookie
veteran
17.5
10 15 12.5
15 15
0
5
10
15
20
25
rookie veteran
starter
relief

27. Interaction and Main Effect for
Pitcher Type
20 10
Starter Relief
rookie
veteran
15
15 15 15
17.5 12.5
0
5
10
15
20
25
rookie veteran
starter
relief

28. Interaction and Two Main Effects
9 11
Starter Relief
rookie
veteran
10
28 12 20
16 14
0
5
10
15
20
25
30
rookie veteran
starter
relief

29. Assumptions of Between
Factor ANOVAs
 DV data are interval or ratio level
 Data are normally distributed
 Variances are equivalent
(homogeneity of variance)
 Independence of observations
 Same statistical ratio
ANOVA =
Treatment Variance
Error Variance

30. Stating Hypotheses
 Two levels of hypotheses
 Main effects
 Hypothesis for each IV
 Hypothesis for Main Effect A (also sometimes called
Main Effect Row)
 Ho: μ1 = μ2 …
 Ha: not all of the μi are equal.
 Hypothesis for Main Effect B (also sometimes called
Main Effect Column)
 Ho: μ1 = μ2 …
 Ha: not all of the μi are equal.

31. Stating Hypotheses
 Hypothesis for Interaction (sometimes written
A*B or Row*Column)
 Hypothesis for each combination of IVs
 Ho: There is no interaction between factors A and
B. All differences are explained by main effects.
 Ha: There is an interaction. The mean difference
between treatments are not what would be
predicted from main effects only

32. Partitioning
 One-Way Subjects
 SSbetween
 SSwithin
 Two-Way Subjects
 SSbetween (divided up)
 SSrow
 SScolumn
 SSrow*column
 SSwithin

33. Computation
N
G
X
2
2
)()()(
222222
N
G
n
T
N
G
n
T
N
G
n
T
column
column
row
row
SStotal
formula df
N - 1
SSrow
SScolumn
SSrow*column
N
G
n
T
row
row
22
SSwithin SStotal – SSrow – SScolumn – SS row*column
a – 1
Where a is
number of rows
b – 1
Where b is
number of columns
(a – 1)(b – 1)
(a)(b)(n-1)
N
G
n
T
column
column
22

34. Example
Starter Relief
Rookie 4
3
3
5
1
0
2
1
Veteran 3
2
1
2
2
3
1
1
Calculate the means for each of
these cells
Rookie/Starter 3.75
Rookie/Relief 1
Veteran/Starter 2
Veteran/Relief 1.75

35. What are the Total df?
Source SS df MS F
Main Effect for Row 9.00
Main Effect for Column 1.00
Interaction 6.25
Error
(within groups)
9.50
Total 25.75

36. What are the Total df?
Source SS df MS F
Main Effect for Row 9.00
Main Effect for Column 1.00
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

37. What are the df row?
Source SS df MS F
Main Effect for Row 9.00
Main Effect for Column 1.00
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

38. What are the df row?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

39. What are the df column?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

40. What are the df column?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

41. What are the df interaction?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25
Error
(within groups)
9.50
Total 25.75 15

42. What are the df interaction?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50
Total 25.75 15

43. What are the df error?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50
Total 25.75 15

44. What are the df error?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

45. What is the MS for row?
Source SS df MS F
Main Effect for Row 9.00 1
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

46. What is the MS for row?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

47. What is the MS for column?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

48. What is the MS for column?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

49. What is the MS interaction?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1
Error
(within groups)
9.50 12
Total 25.75 15

50. What is the MS interaction?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12
Total 25.75 15

51. What is the MS error?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12
Total 25.75 15

52. What is the MS error?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

53. What is the main effect for row?
Source SS df MS F
Main Effect for Row 9.00 1 9.00
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

54. What is the main effect for row?
Source SS df MS F
Main Effect for Row 9.00 1 9.00 11.37
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

55. What is the main effect for column?
Source SS df MS F
Main Effect for Row 9.00 1 9.00 11.37
Main Effect for Column 1.00 1 1.00
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

56. What is the main effect for column?
Source SS df MS F
Main Effect for Row 9.00 1 9.00 11.37
Main Effect for Column 1.00 1 1.00 1.26
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

57. What is the interaction?
Source SS df MS F
Main Effect for Row 9.00 1 9.00 11.37
Main Effect for Column 1.00 1 1.00 1.26
Interaction 6.25 1 6.25
Error
(within groups)
9.50 12 0.79
Total 25.75 15

58. What is the interaction?
Source SS df MS F
Main Effect for Row 9.00 1 9.00 11.37
Main Effect for Column 1.00 1 1.00 1.26
Interaction 6.25 1 6.25 7.90
Error
(within groups)
9.50 12 0.79
Total 25.75 15

59. Example
 Critical Value
 For each test use the df associated with it.
 Is not necessarily the same for all three tests
although in our example it is.
 4.747
 Evaluate each effect separately

60.  Is Main Effect row sig?
 Yes
 No

61.  Is Main Effect column sig?
 Yes
 No

62.  Is Interaction sig?
 Yes
 No

63. Now what?
 If you have no significant interaction, then
you can talk about what main effects are
significant in the same way that you evaluated
one-way ANOVAs.
 If the interaction is significant you must be
careful interpreting main effects. The main
effect could be present simply because of the
interaction. So concentrate on the interaction
interpretation.

64. Now what?
 If it is a 2X2 ANOVA and the interaction is
significant then graph the means and interpret.
 Our example
0
0.5
1
1.5
2
2.5
3
3.5
4
starter relief
rookie
veteran

65. Now what?
 If interaction is significant
 Plot interaction
 Interpret interaction
 Level of one IV is influenced by level of a
second IV
 If Main Effects are significant
 Conduct Post Hoc tests
 Report results
 Effect sizes
• Use omega squared to report effect size