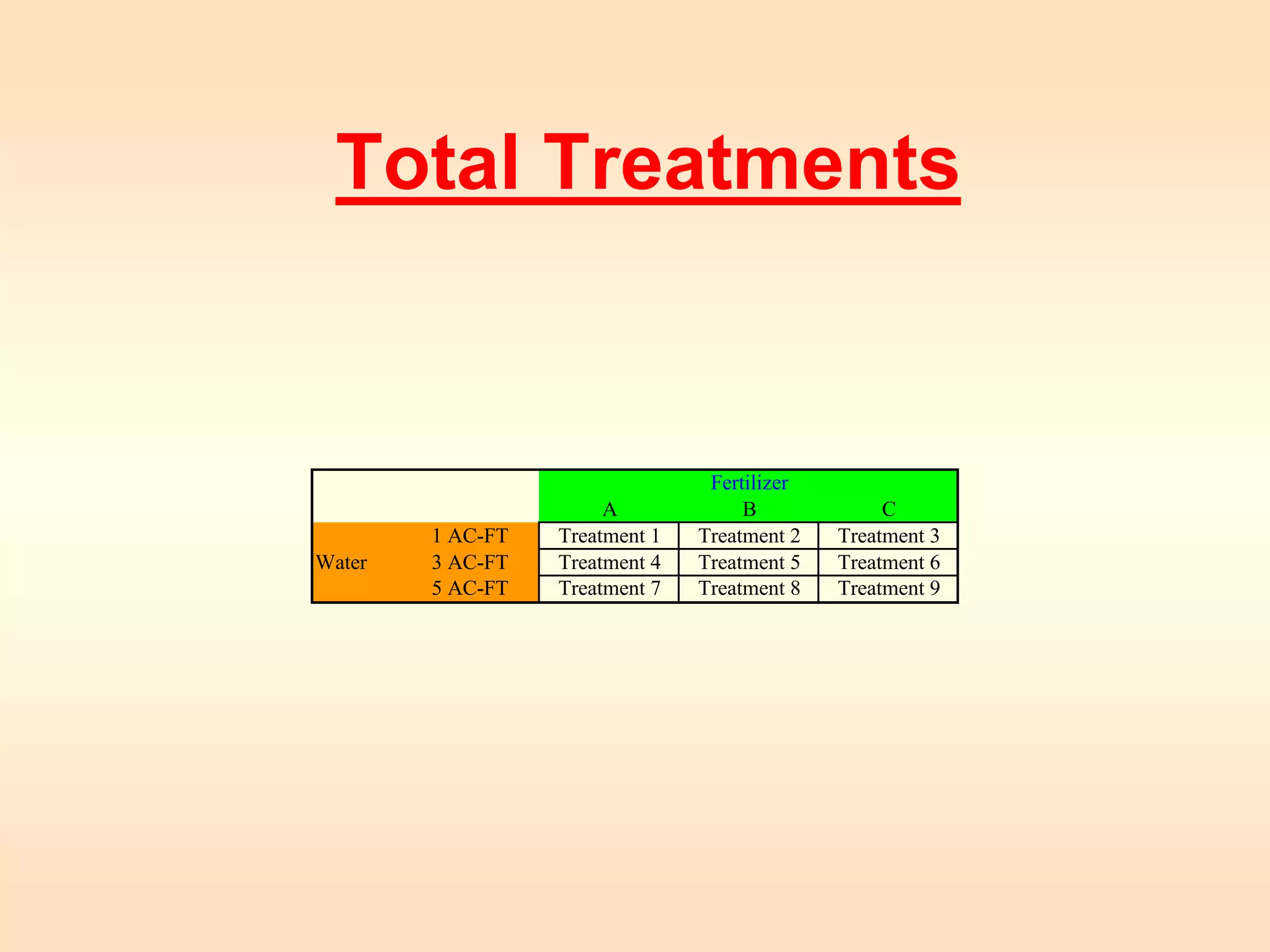
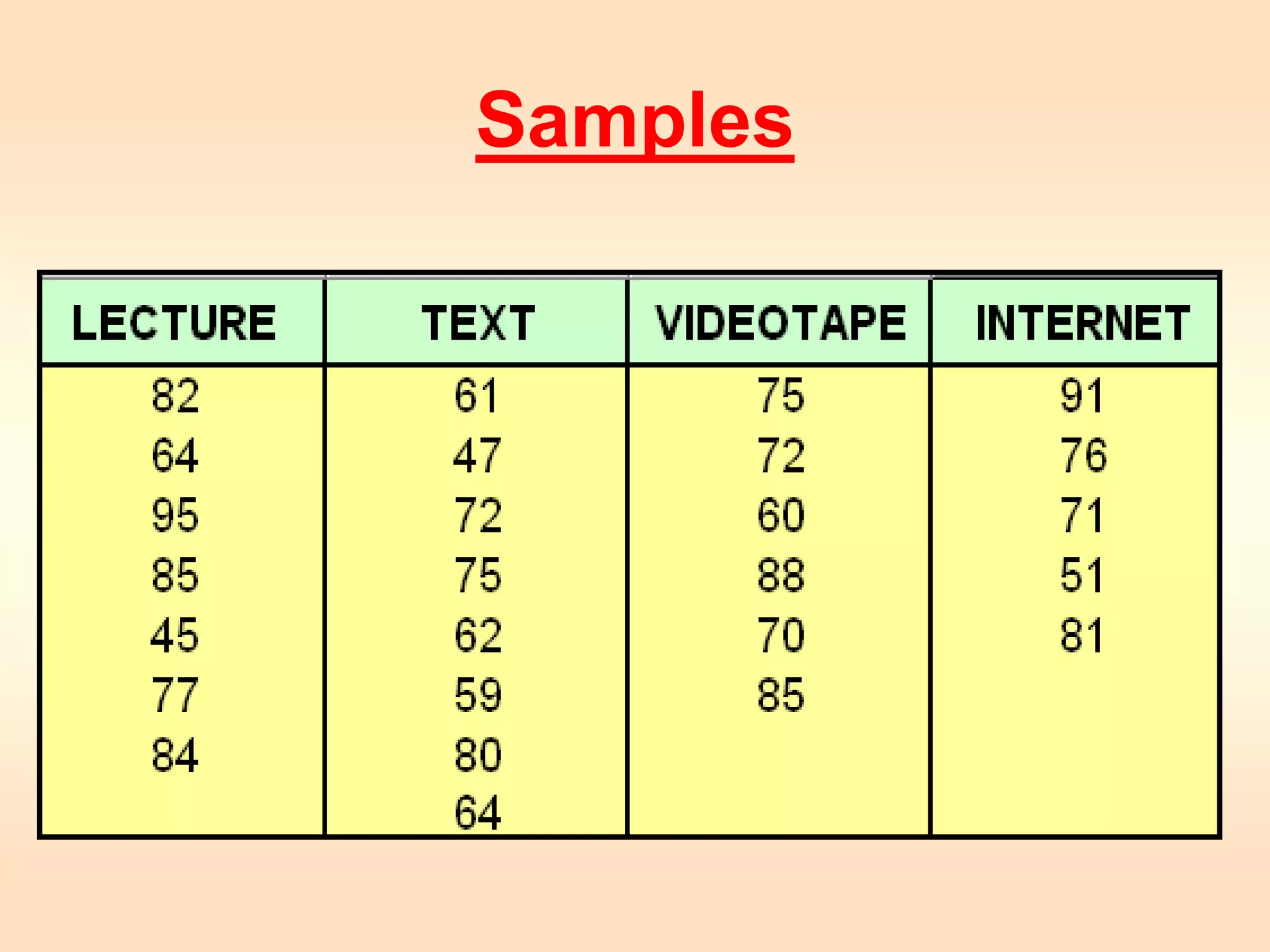
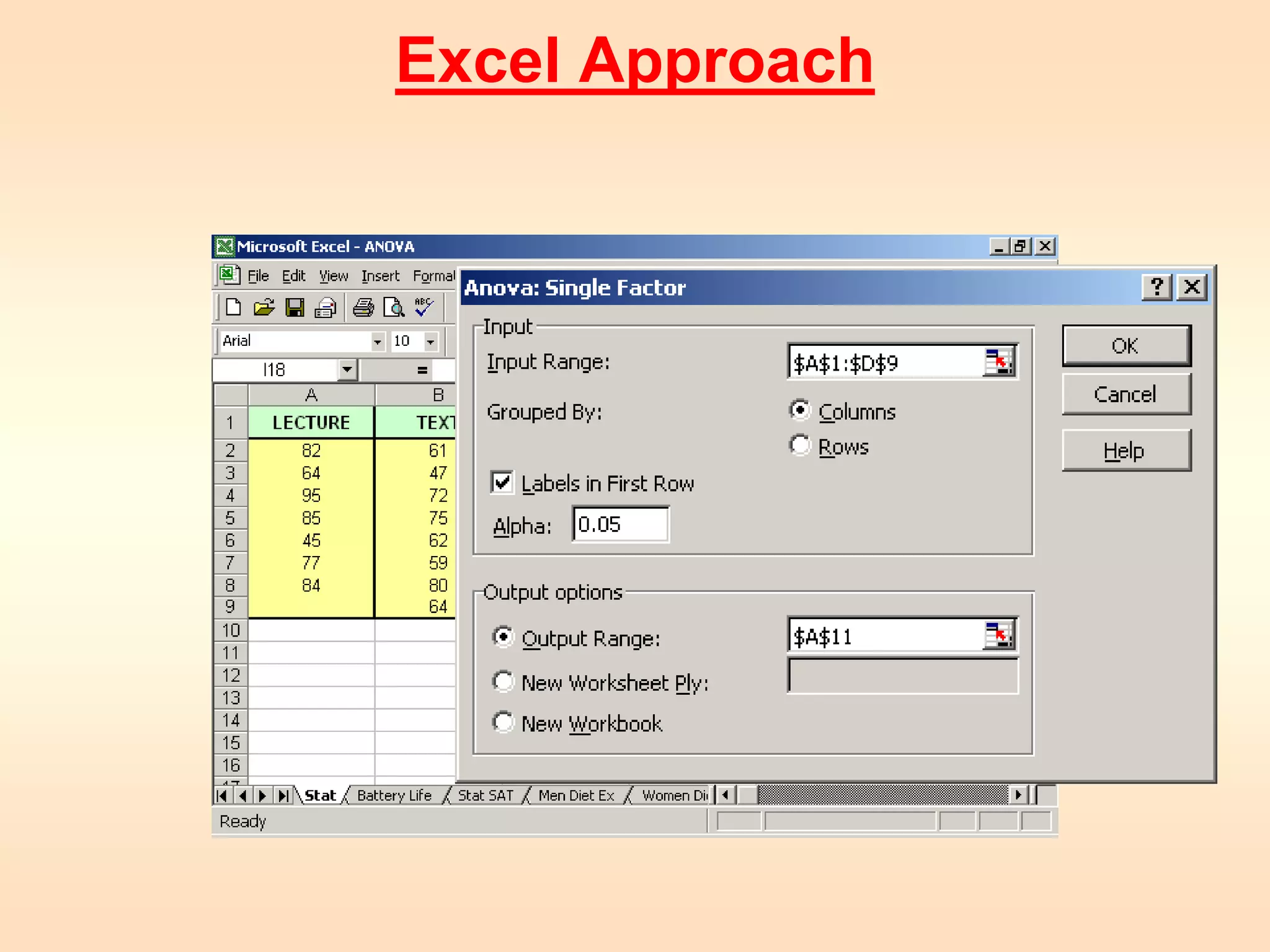
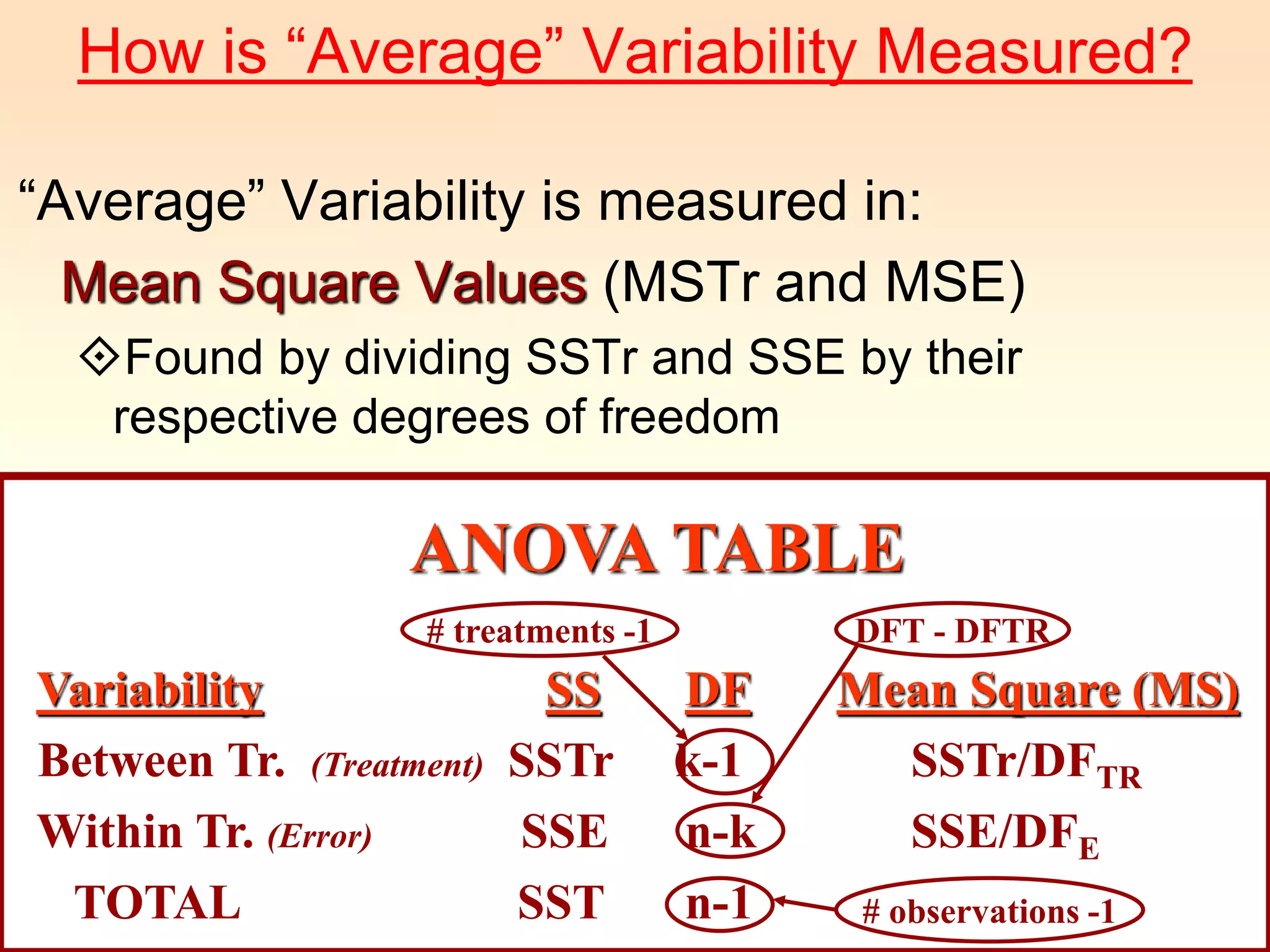
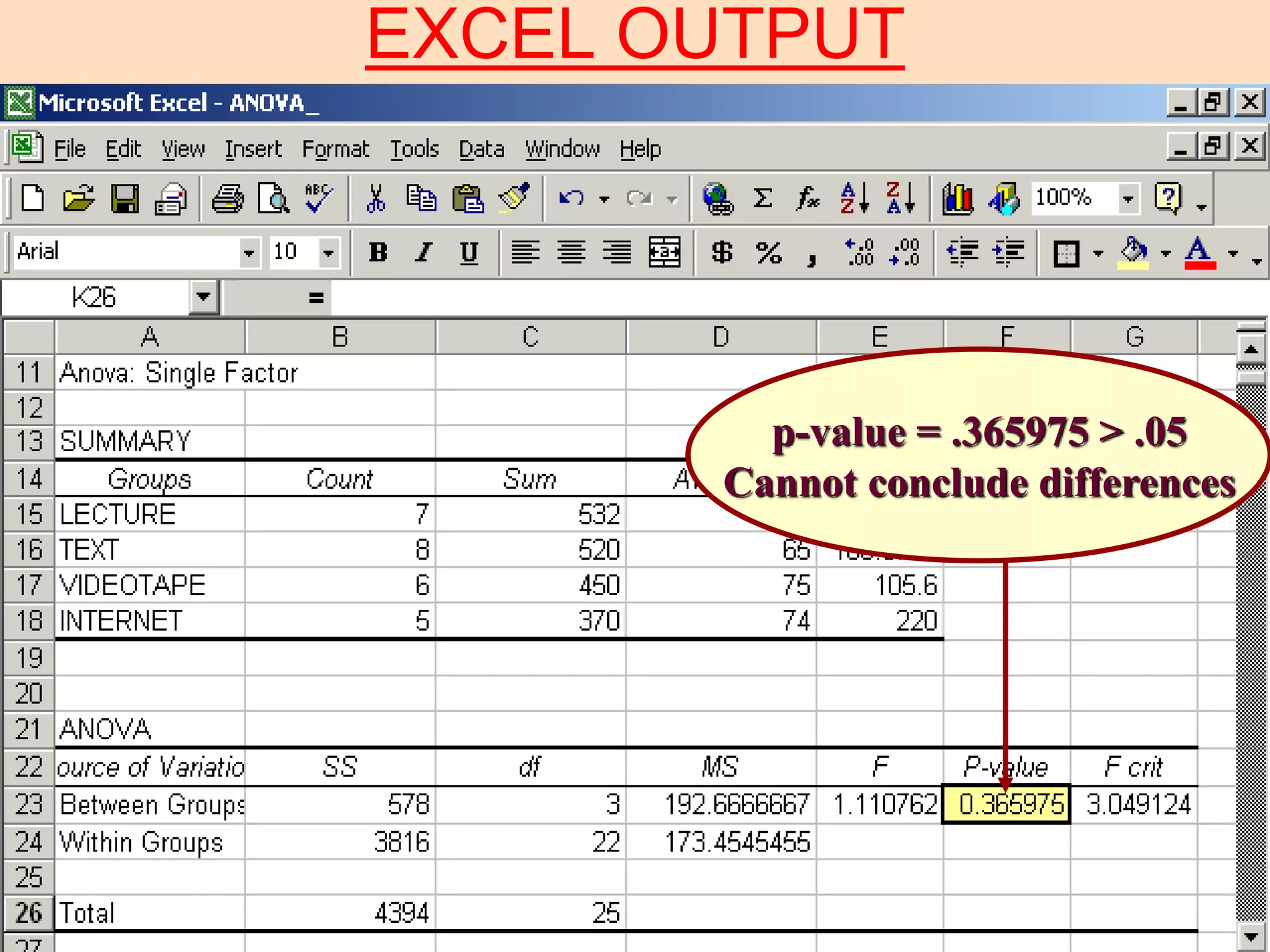
1) ANOVA is used to compare the means of more than two populations and determine if observed differences are due to chance or actual differences in the population means. 2) The document provides an example of using a one-way single factor ANOVA to analyze the effects of different teaching formats on student exam scores. 3) The ANOVA compares the between-treatment variability to the within-treatment variability using an F-test. If the between-treatment variability is significantly larger, it suggests the population means differ. In this example, the F-test showed no significant difference between the teaching formats.

1. ANOVA
One way Single Factor Models
KARAN DESAI-11BIE001
DHRUV PATEL-11BIE024
VISHAL DERASHRI -11BIE030
HARDIK MEHTA-11BIE037
MALAV BHATT-11BIE056

2. DEFINITION
Analysis of variance (ANOVA) is a collection of
statistical models used to analyze the differences
between group means and their associated procedures
(such as "variation" among and between groups),
developed by R.A.Fisher .In the ANOVA setting, the
observed variance in a particular variable is partitioned
into components attributable to different sources of
variation
2

3. -Sir Ronald
Aylmer Fisher
FRS was an English statistician,
evolutionary biologist, geneticist, and
3

4. Why ANOVA
• Compare the mean of more than two
population?
• Compare populations each containing
several subgroups or levels?
4

5. Problem with multiple T test
• One problem with this approach is the increasing
number of tests as the number of groups
increases
• The probability of making a Type I error increases
as the number of tests increase.
• If the probability of a Type I error for the analysis
is set at 0.05 and 10 t-tests are done, the overall
probability of a Type I error for the set of tests = 1
– (0.95)10 = 0.40* instead of 0.05
5

6. In its simplest form, ANOVA provides a statistical test of
whether or not the means of several groups are equal,
and therefore generalizes the t-test to more than two
groups. As doing multiple two-sample t-tests would result
in an increased chance of committing a statistical type-I
error, ANOVAs are useful in comparing (testing) three or
more means (groups or variables) for statistical
significance.
6

7. • Another way to describe the multiple comparisons
problem is to think about the meaning of an alpha
level = 0.05
• Alpha of 0.05 implies that, by chance, there will be
one Type I error in every 20 tests: 1/20 = 0.05.
• This means that, by chance the null hypothesis
will be incorrectly rejected once in every 20 tests
• As the number of tests increases, the probability
of finding a ‘significant’ result by chance increases.
7

8. Importance of ANOVA
• The ANOVA is an important test because
it enables us to see for example how
effective two different types of treatment
are and how durable they are.
• Effectively a ANOVA can tell us how well a
treatment work, how long it lasts and how
budget friendly it will be an
8

9. CLASSIFICATION OF ANOVA
MODEL
1. Fixed-effects models:
The fixed-effects model of analysis of
variance applies to situations in which the experimenter
applies one or more treatments to the subjects of the
experiment to see if the response variable values
change. This allows the experimenter to estimate the
ranges of response variable values that the treatment
would generate in the population as a whole.
9

10. 2. Random-effects model:
Random effects models are used
when the treatments are not fixed. This occurs when the
various factor levels are sampled from a larger
population. Because the levels themselves are random
variables , some assumptions and the method of
contrasting the treatments (a multi-variable
generalization of simple differences) differ from the fixed-effects
model.
10

11. 3.Mixed-effects models
A mixed-effects model contains experimental
factors of both fixed and random-effects types, with appropriately
different interpretations and analysis for the two types.
Example: Teaching experiments could be performed by a
university department to find a good introductory textbook, with
each text considered a treatment. The fixed-effects model would
compare a list of candidate texts. The random-effects model
would determine whether important differences exist among a
list of randomly selected texts. The mixed-effects model would
compare the (fixed) incumbent texts to randomly selected
alternatives.
11

12. ASSUMPTION
Normal distribution
Variances of dependent variable are equal in all
populations
Random samples; independent scores
12

13. One way Single factor ANOVA
13

14. ONE-WAY ANOVA
One factor (manipulated variable)
One response variable
Two or more groups to compare
14

15. USEFULLNESS
Similar to t-test
More versatile than t-test
Compare one parameter (response variable)
between two or more groups
15

16. Remember that…
Standard deviation (s)
n
s = √[(Σ (xi – X)2)/(n-1)]
i = 1
In this case: Degrees of freedom (df)
df = Number of observations or groups
16

17. ANOVA
ANOVA (ANalysis Of VAriance) is a natural extension used to
compare the means more than 2 populations.
Basic Question: Even if the true means of n populations were
equal (i.e. m1 = m2 = m3 = m4) we cannot expect the sample
means (x1, x2, x3, x4 ) to be equal. So when we get
different values for the x’s,
How much is due to randomness?
How much is due to the fact that we are sampling from
different populations with possibly different mj’s.

18. ANOVA TERMINOLOGY
Response Variable (y)
What we are measuring
Experimental Units
The individual unit that we will measure
Factors
Independent variables whose values can change to affect
the outcome of the response variable, y
Levels of Factors
Values of the factors
Treatments
The combination of the levels of the factors applied to an
experimental unit

19. Example
We want to know how combinations of different
amounts of water (1 ac-ft, 3 ac-ft, 5 ac-ft) and
different fertilizers (A, B, C) affect crop yields
Response variable
– crop yield (bushels/acre)
Experimental unit
Each acre that receives a treatment
Factors (2)
Water and fertilizer
Levels (3 for Water; 3 for Fertilizer)
Water: 1, 3, 5; Fertilizer: A, B, C
Treatments (9 = 3x3)
1A, 3A, 5A, 1B, 3B, 5B, 1C, 3C, 5C

20. Total Treatments
Fertilizer
A B C
1 AC-FT Treatment 1 Treatment 2 Treatment 3
Water 3 AC-FT Treatment 4 Treatment 5 Treatment 6
5 AC-FT Treatment 7 Treatment 8 Treatment 9

21. Single Factor ANOVA
Basic Assumptions
 If we focus on only one factor (e.g. fertilizer type in the
previous example), this is called single factor ANOVA.
 In this case, levels and treatments are the same thing since
there are no combinations between factors.
 Assumptions for Single Factor ANOVA
1. The distribution of each population in the comparison has a
normal distribution
2. The standard deviations of each population (although
unknown) are assumed to be equal (i.e. s1 = s2 = s3 = s4)
3. Sampling is:
Random
Independent

22. Example
The university would like to know if the delivery mode of the
introductory statistics class affects the performance in the
class as measured by the scores on the final exam.
The class is given in four different formats:
Lecture
Text Reading
Videotape
Internet
The final exam scores from random samples of students from
each of the four teaching formats was recorded.

23. Samples

24. Summary
There is a single factor under observation – teaching format
There are k = 4 different treatments (or levels of teaching
formats)
The number of observations (experimental units) are n1 = 7,
n2 = 8, n3 = 6, n4 = 5 total number of
observations, n = 26
Treatment Means : x1 = 76, x2 = 65, x3 = 75, x4 =
74
Grand mean (of all 26 observations) : x =
72

25. Why aren’t all thex’s the same?
There is variability due to the different treatments --
Between Treatment Variability (Treatment)
There is variability due to randomness within each
treatment -- Within Treatment Variability (Error)
BASIC CONCEPT
If the average Between Treatment Variability is “large”
compared to the average Within Treatment Variability,
we can reasonably conclude that there really are
differences among the population means (i.e. at least
one μj differs from the others).

26. Basic Questions
Given this basic concept, the natural questions are:
What is “variability” due to treatment and due to error
and how are they measured?
What is “average variability” due to treatment and due
to error and how are they measured?
What is “large”?
How much larger than the observed average
variability due to error does the observed average
variability due to treatment have to be before we
are convinced that there are differences in the true
population means (the μ’s)?

27. How Is “Total” Variability
Measured?
Variability is defined as the Sum of Square Deviations (from the
grand mean). So,
SST (Total Sum of Squares)
 Sum of Squared Deviations of all observations from the
grand mean. (McClave uses SSTotal)
SSTr (Between Treatment Sum of Squares)
Sum of Square Deviations Due to Different Treatments.
(McClave uses SST)
SSE (Within Treatment Sum of Squares)
Sum of Square Deviations Due to Error
SST = SSTr + SSE

28. How is “Average” Variability Measured?
“Average” Variability is measured in:
Mean Square Values (MSTr and MSE)
Found by dividing SSTr and SSE by their
respective degrees of freedom
ANOVA TABLE
# treatments -1 DFT - DFTR
Variability SS DF Mean Square (MS)
Between Tr. (Treatment) SSTr k-1 SSTr/DFTR
Within Tr. (Error) SSE n-k SSE/DFE
TOTAL SST n-1
# observations -1

29. Formula for Calculating
SST
Calculating SST
Just like the
numerator of the
variance
assuming all (26)
entries come
from one
population
= 
SST (x x)
ij
2 2
2
82 72) ... (81 72) 4394
=     =

30. Formula for Calculating
SSTr
Calculating SSTr
Between Treatment
Variability
Replace all entries within
each treatment by its
mean – now all the
variability is between (not
within) treatments
76
76
76
76
76
76
76
= 
SSTr n (x x)
2
j j
75
75
75
75
75
75
65
65
65
65
65
65
65
65
2 2 2 2
=        =
7(76 72) 8(65 72) 6(75 72) 5(74 72) 578
74
74
74
74
74

31. Formula for Calculating
SSE
Calculating SSE (Within Treatment Variability)
The difference between the SST and SSTr ---
SSE SST - SSTr
= =
4394 - 578 =
3816

32. Can we Conclude a Difference Among
the 4 Teaching Formats?
We conclude that at least one population mean differs
from the others if the average between treatment
variability is large compared to the average within
treatment variability, that is if MSTr/MSE is “large”.
The ratio of the two measures of variability for these
normally distributed random variables has an F
distribution and the F-statistic (=MSTr/MSE) is
compared to a critical F-value from an F distribution
with:
Numerator degrees of freedom = DFTr
Denominator degrees of freedom = DFE
If the ratio of MSTr to MSE (the F-statistic) exceeds
the critical F-value, we can conclude that at least one
population mean differs from the others.

33. Can We Conclude Different Teaching
Formats Affect Final Exam Scores?
The F-test
H0: m1 = m2 = m3 = m4
HA: At least one mj differs from the others
Select α = .05.
Reject H0 (Accept HA) if:
F =  α,DFTr,DFE = .05,3,22 =
F F 3.05
MSTr
MSE

34. Hand Calculations for the F-test
173.45
578
= = =
3816
22
SSTr
SSE
DFE
MSE
192.67
3
DFTr
MSTr
= = =
1.11
192.67
= =
173.45
1.11 3.05
F

Cannot conclude there is a difference among the μj’s

35. Excel Approach

36. EXCEL OUTPUT
p-value = .365975 > .05
Cannot conclude differences

37. REVIEW
ANOVA Situation and Terminology
Response variable, Experimental Units, Factors,
Levels, Treatments, Error
Basic Concept
If the “average variability” between treatments is “a
lot” greater than the “average variability” due to error –
conclude that at least one mean differs from the
others.
Single Factor Analysis
By Hand
By Excel