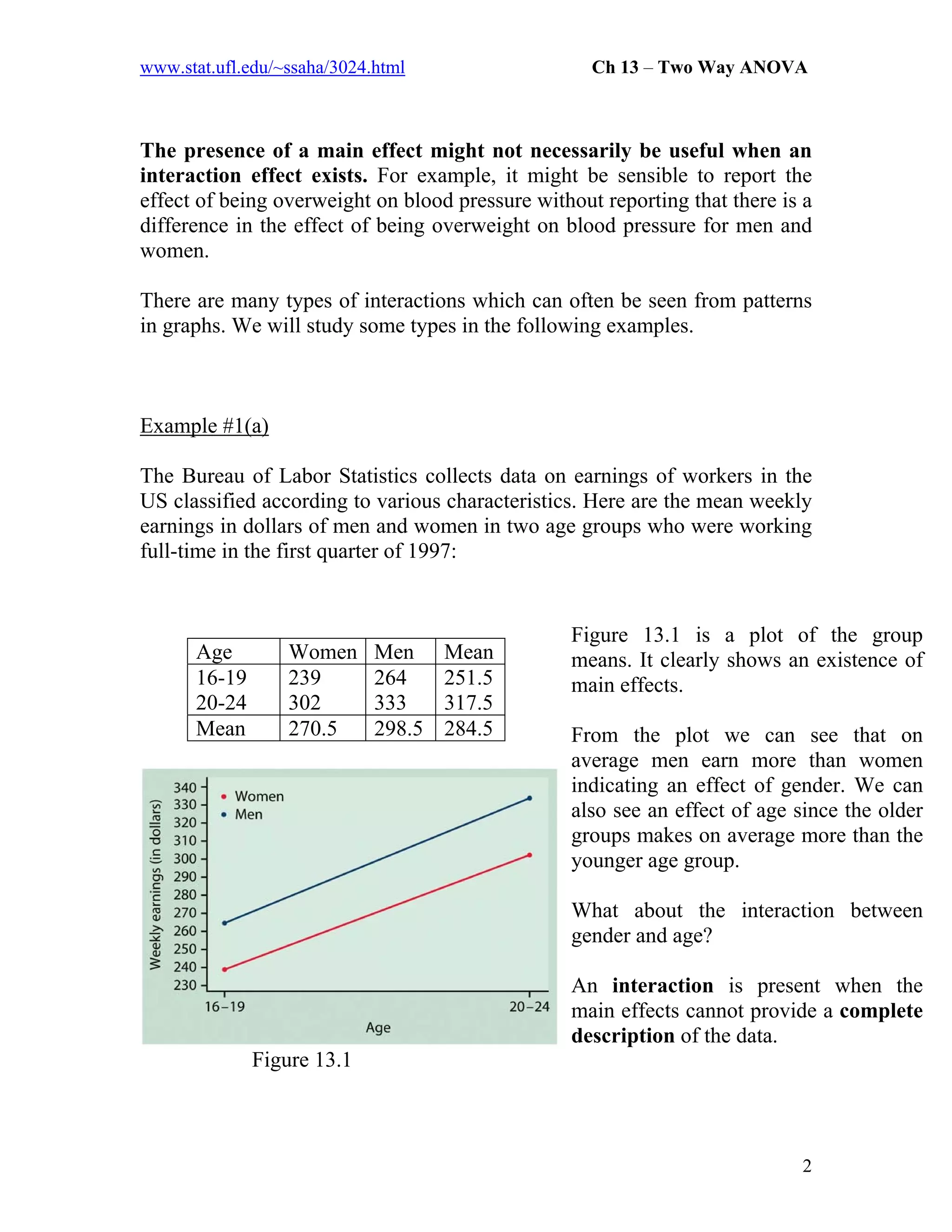
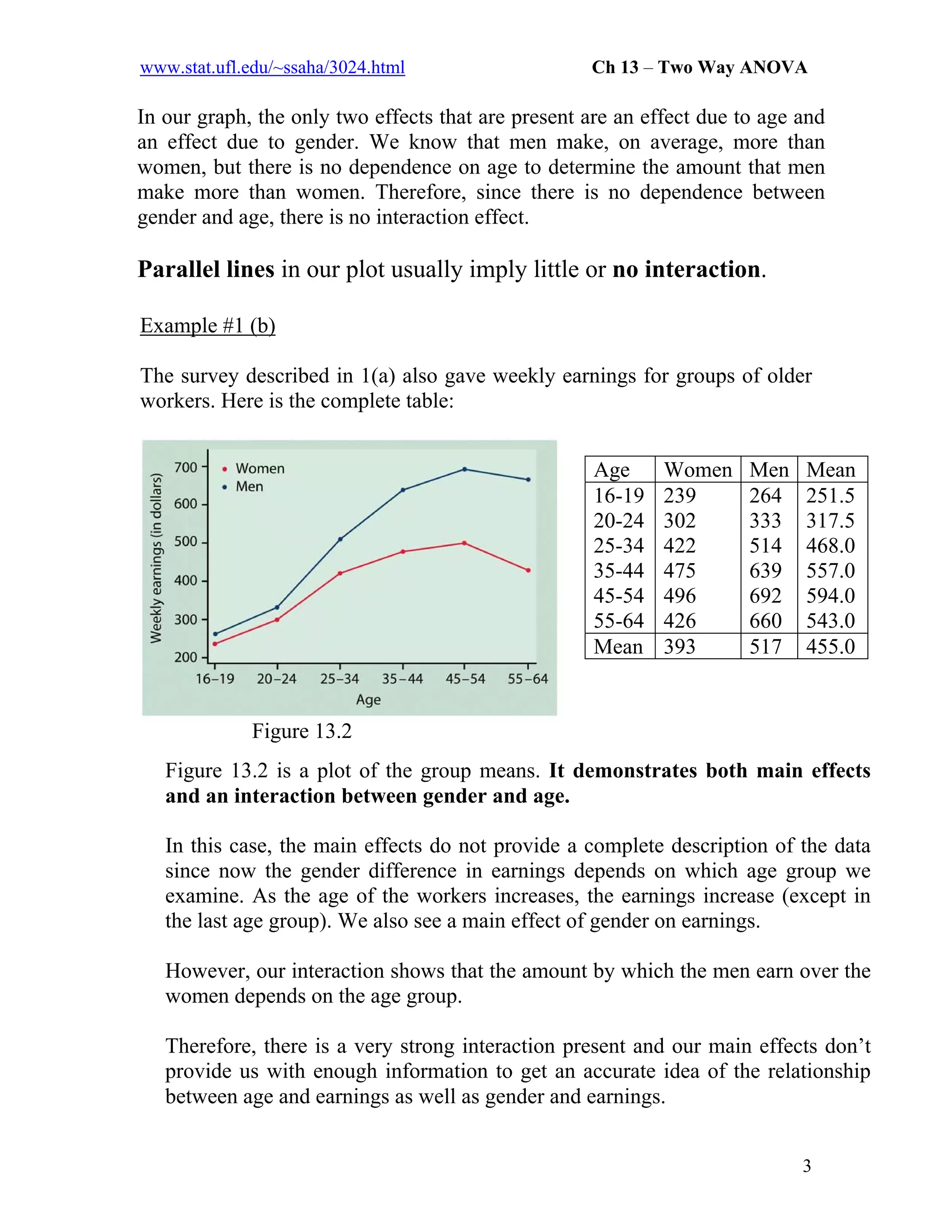
The document explains two-way analysis of variance (ANOVA), highlighting its efficiency in examining the effects and interactions of two factors in a dataset. It emphasizes the terms main effect and interaction and provides several examples, illustrating how to interpret and analyze data collected from studies. Additionally, it includes details on model formulation, parameter estimation, and the necessary hypotheses for testing main effects and interactions.