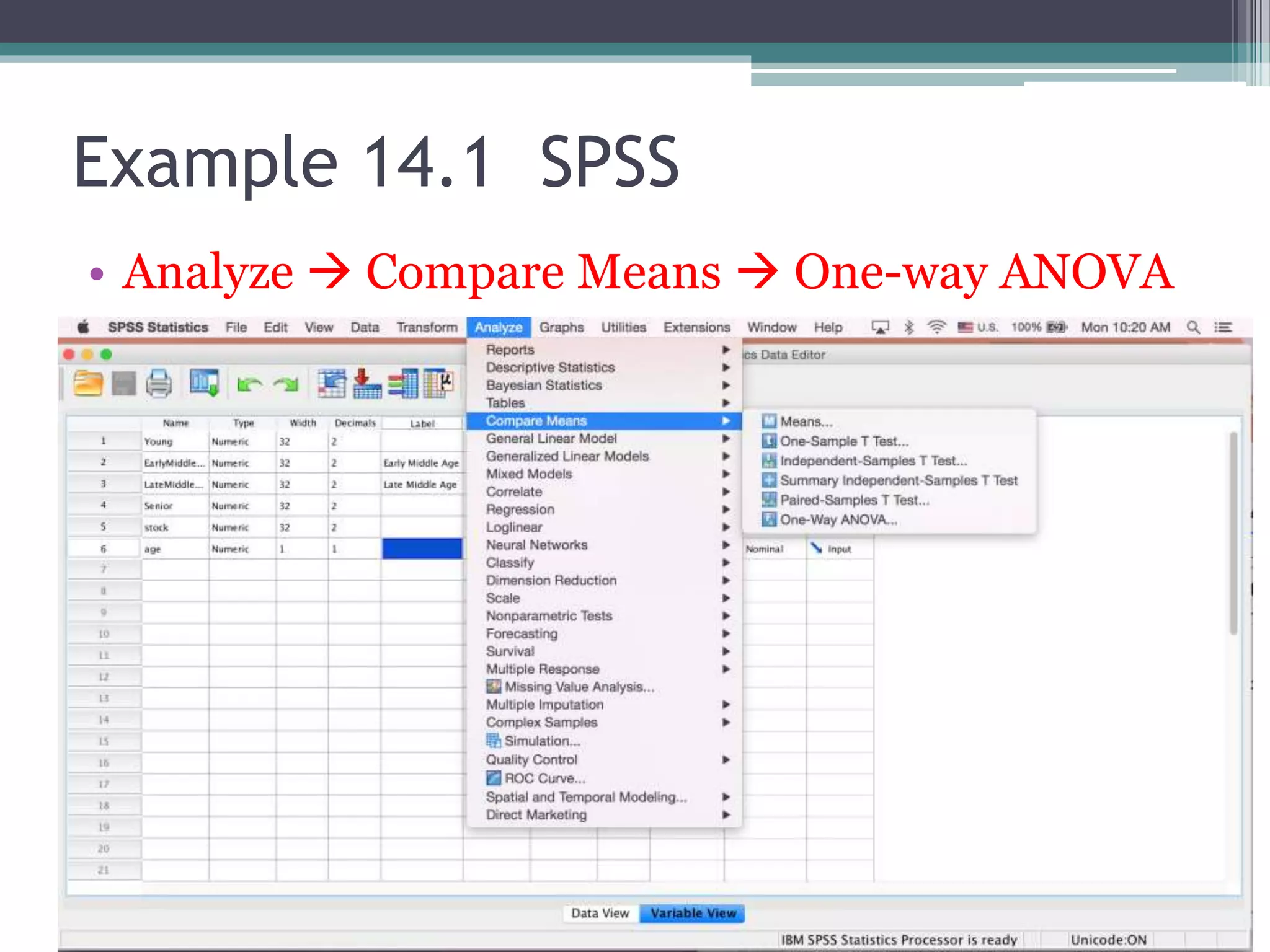
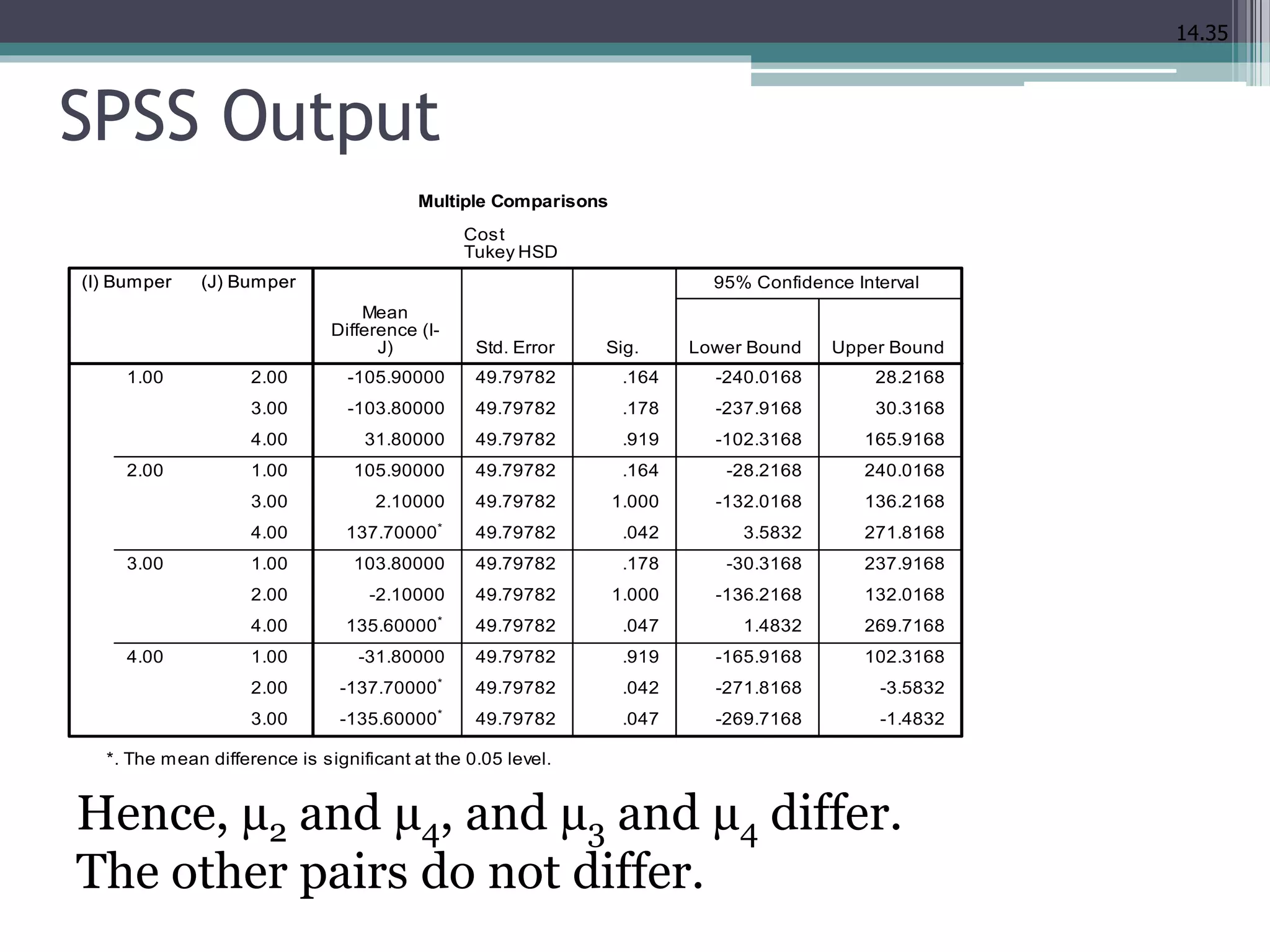
This document discusses quantitative research methods and analysis of variance (ANOVA). It covers one-way ANOVA, which allows comparison of three or more groups, and examples comparing differences between age groups and types of bumpers. Requirements for ANOVA like normality and independence are addressed. Post-hoc tests for identifying specific group differences are also introduced.