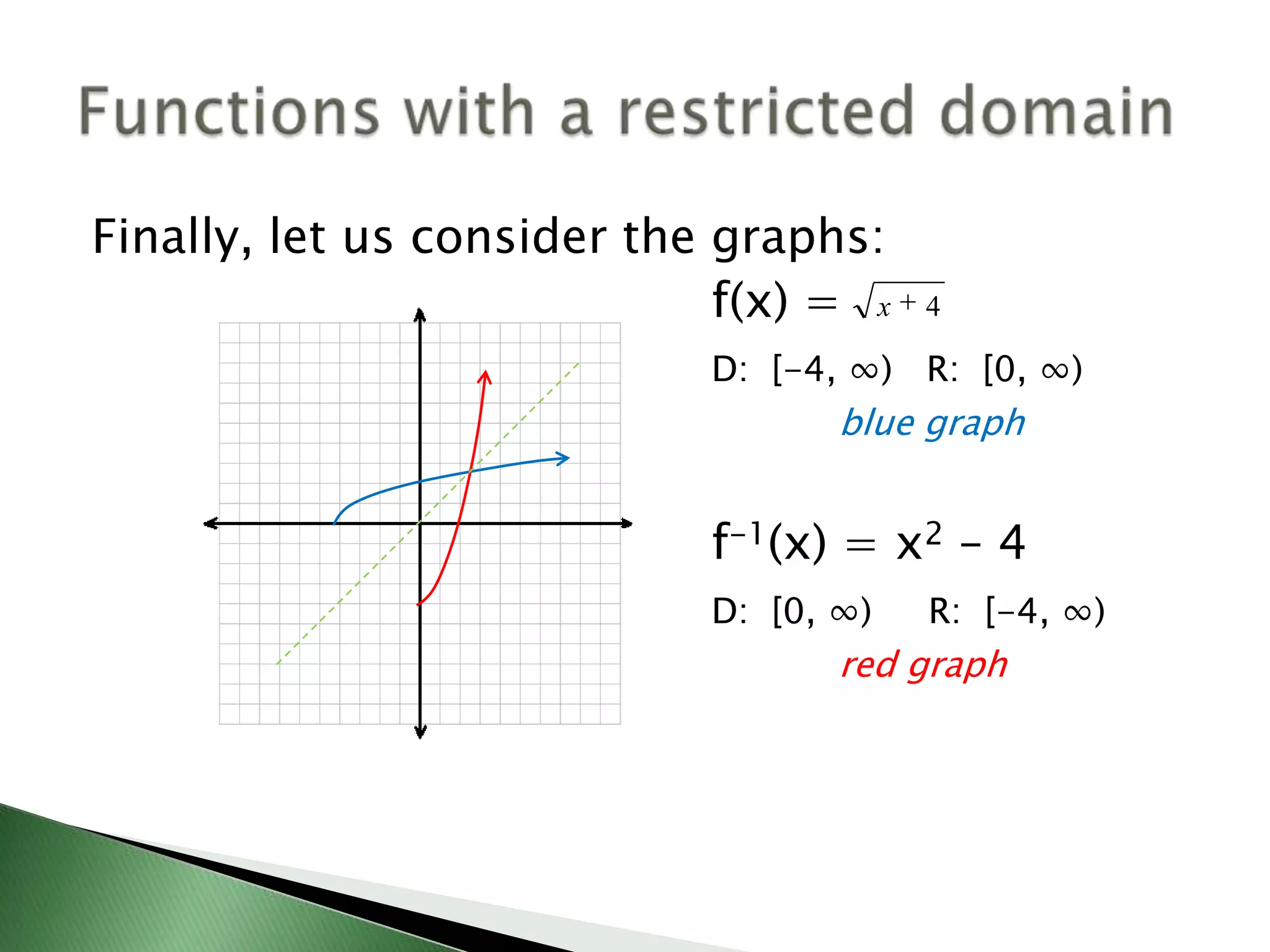
1) The document discusses finding the inverse of functions by interchanging the x and y variables and solving for y. It provides examples of finding the inverses of f(x)=3x-7 and g(x)=2x^3+1. 2) It also discusses verifying inverses by checking if the composition of a function and its inverse equals x. And finding inverses of functions with restricted domains, including an example of f(x)=sqrt(x+4). 3) Finally, it discusses the relationship between a function being one-to-one and having an inverse function, both algebraically and graphically.

1. Inverse FunctionsFinding the Inverse

2. 1st example, begin with your function f(x) = 3x – 7 replace f(x) with y y = 3x - 7Interchange x and y to find the inverse x = 3y – 7 now solve for y x + 7 = 3y = y f-1(x) = replace y with f-1(x)Finding the inverse

3. 2nd example g(x) = 2x3 + 1 replace g(x) with y y = 2x3 + 1Interchange x and y to find the inverse x = 2y3 + 1 now solve for y x - 1 = 2y3 = y3= y g-1(x) = replace y with g-1(x)Finding the inverse

4. Recall, to verify you have found the inverse you check that composition of the function with the inverse, in both orders, equals xUsing specific ordered pairs can illustrate how the inverse works, but does not verify that it is the inverse.Verifying inverses

5. Consider f(x) =What is the domain? x + 4 > 0 x > -4 or the interval [-4, ∞)What is the range? y > 0 or the interval [0, ∞)Function with a restricted domain

6. Now find the inverse: f(x) = D: [-4, ∞) R: [0, ∞) y =Interchange x and y x = x2 = y + 4 x2 – 4 = y f-1(x) = x2 – 4 D: [0, ∞) R: [-4, ∞)Function with a restricted domain

7. Finally, let us consider the graphs: f(x) =D: [-4, ∞) R: [0, ∞) blue graph f-1(x) = x2 – 4 D: [0, ∞) R: [-4, ∞) red graphFunctions with a restricted domain

8. 2nd exampleConsider g(x) = 5 - x2 D: [0, ∞)What is the range? Make a very quick sketch of the graph R: (-∞, 5]Function with a restricted domain

9. Now find the inverse: g(x) = 5 - x2 D: [0, ∞) R: (-∞, 5] y = 5 - x2Interchange x and y x = 5 - y2 x – 5 = -y2 5 – x = y2 = ybut do we want the + or – square root? g-1(x) = D: (-∞, 5] R: [0, ∞) Function with a restricted domain

10. And, now the graphs: g(x) = 5 - x2 D: [0, ∞) R: (-∞, 5] blue graph g-1(x) = D: (-∞, 5] R: [0, ∞) red graphFunctions with a restricted domain

11. A function is one-to-one if each x and y-value is uniqueAlgebraically it means if f(a)=f(b), then a=b.On a graph it means the graph passes the vertical and the horizontal line tests.If a function is one-to-one it has an inverse function.One-to-one