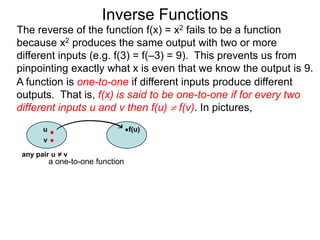
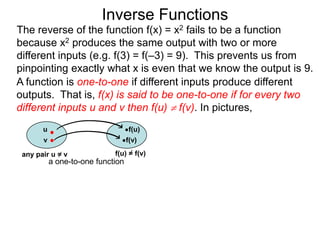
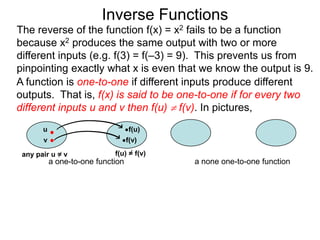
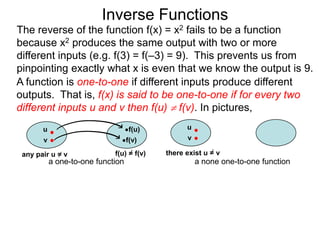
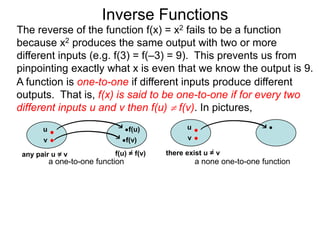
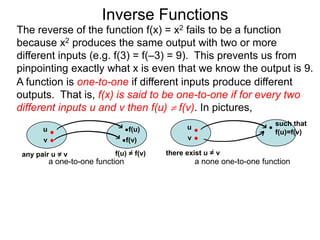
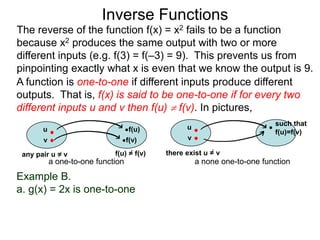
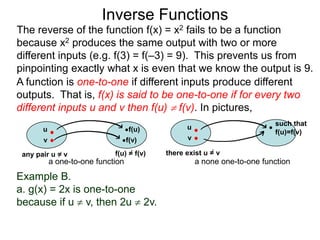
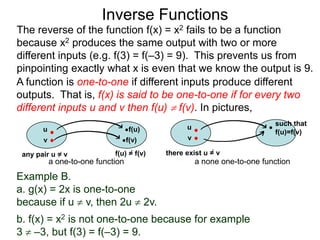
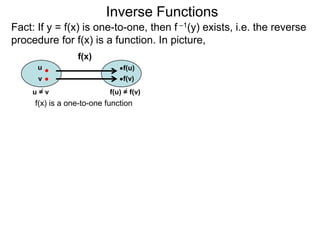
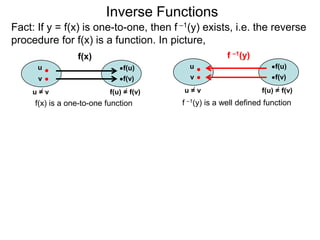
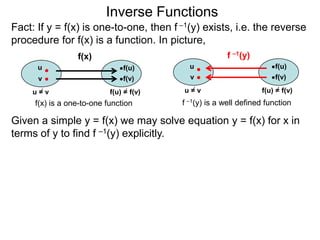
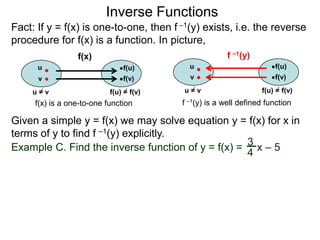
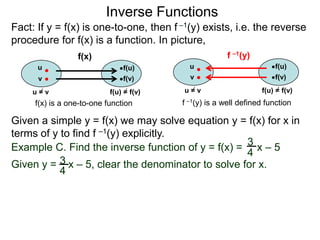
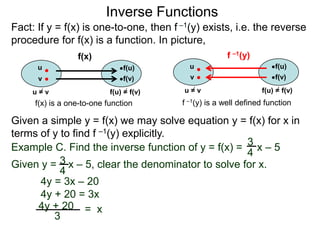
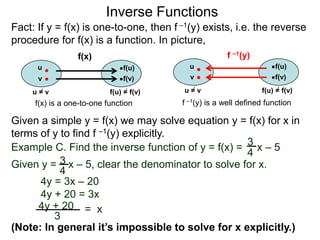
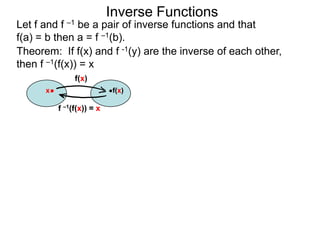
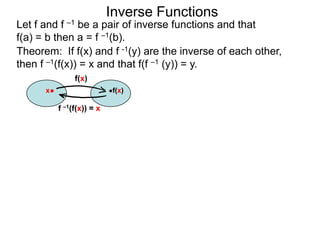
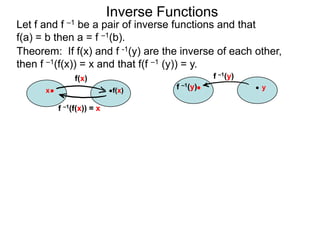
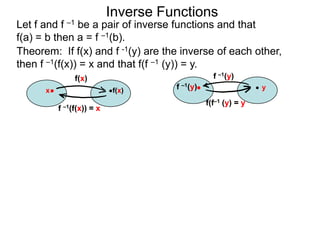
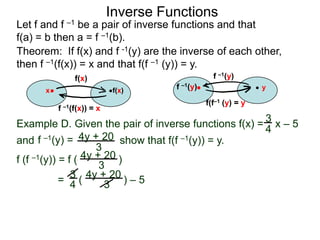
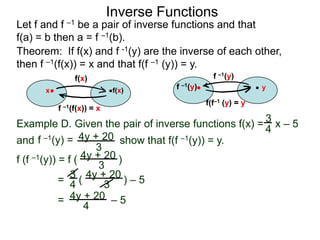
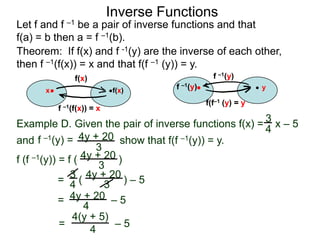
The document discusses inverse functions. An inverse function f-1(y) takes an output y of a function f(x) and returns the corresponding input(s) x. For a function f(x) to have an inverse function, it must be one-to-one, meaning that different inputs map to different outputs. The inverse of the function f(x) = x2 is not a function because x2 is not one-to-one - it maps both 3 and -3 to the same output of 9. A function g(x) = 2x is one-to-one and would have an inverse function, because different inputs always map to different outputs under multiplication by 2. If a function







































![Inverse Functions
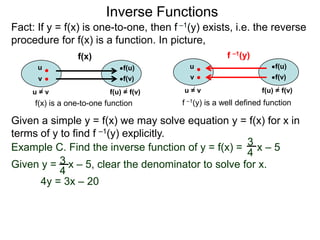
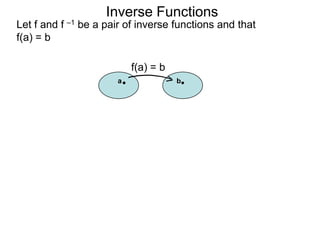
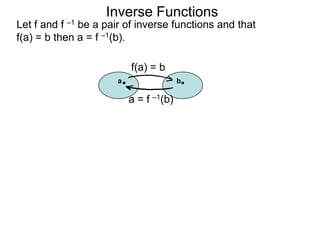
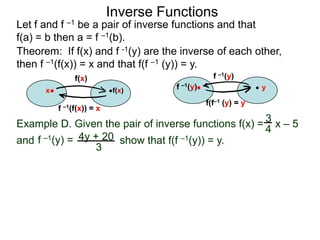
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2–x
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x+1 clear denominator
[( 2 – x ) + 1 ] (2 – x)](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-71-320.jpg)
![Inverse Functions
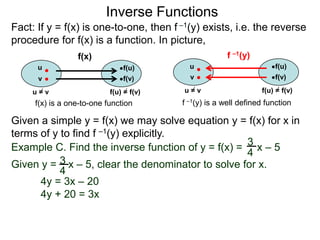
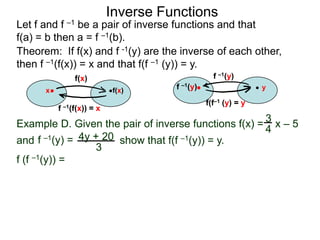
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2–x
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x+1 clear denominator
[( 2 – x ) + 1 ] (2 – x)](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-72-320.jpg)
![Inverse Functions
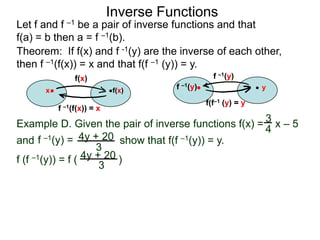
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2 – x (2 – x)
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x + 1 (2 – x) clear denominator
[( 2 – x ) + 1 ] (2 – x)](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-73-320.jpg)
![Inverse Functions
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2 – x (2 – x)
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x + 1 (2 – x) clear denominator
[( 2 – x ) + 1 ] (2 – x)
2(x + 1) – (2 – x)
=
(x + 1) + (2 – x)](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-74-320.jpg)
![Inverse Functions
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2 – x (2 – x)
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x + 1 (2 – x) clear denominator
[( 2 – x ) + 1 ] (2 – x)
2(x + 1) – (2 – x)
=
(x + 1) + (2 – x)
2x + 2 – 2 + x
= x+1+2–x](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-75-320.jpg)
![Inverse Functions
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2 – x (2 – x)
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x + 1 (2 – x) clear denominator
[( 2 – x ) + 1 ] (2 – x)
2(x + 1) – (2 – x)
=
(x + 1) + (2 – x)
2x + 2 – 2 + x
= x+1+2–x
= 3x = x
3](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-76-320.jpg)
![Inverse Functions
b. Show that f(f –1(x)) = x.
We have f (x) = 2x – 1 and that f–1(x) = 2 – x
x+1
x+1
Hence that f(f –1(x)) = f( x + 1 )
2 – x (2 – x)
x + 1)
[ 2(2 – x – 1 ] (2 – x)
= x + 1 (2 – x) clear denominator
[( 2 – x ) + 1 ] (2 – x)
2(x + 1) – (2 – x)
=
(x + 1) + (2 – x)
2x + 2 – 2 + x
= x+1+2–x
= 3x = x
3
Your turn: verify that f–1 (f (x)) = x.](https://image.slidesharecdn.com/3inversefunctionoptional-130123192559-phpapp02/85/53-inverse-function-optional-77-320.jpg)