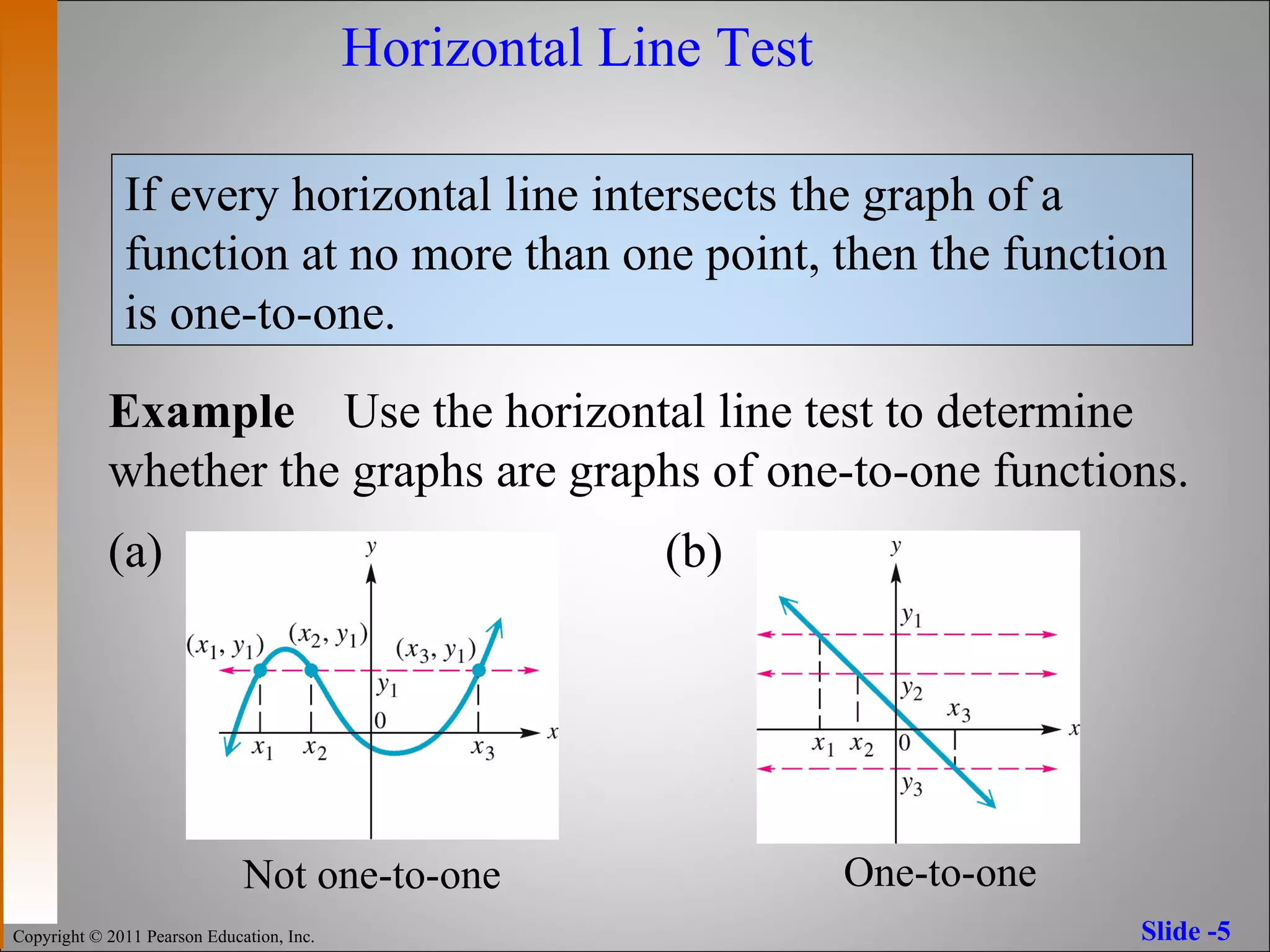
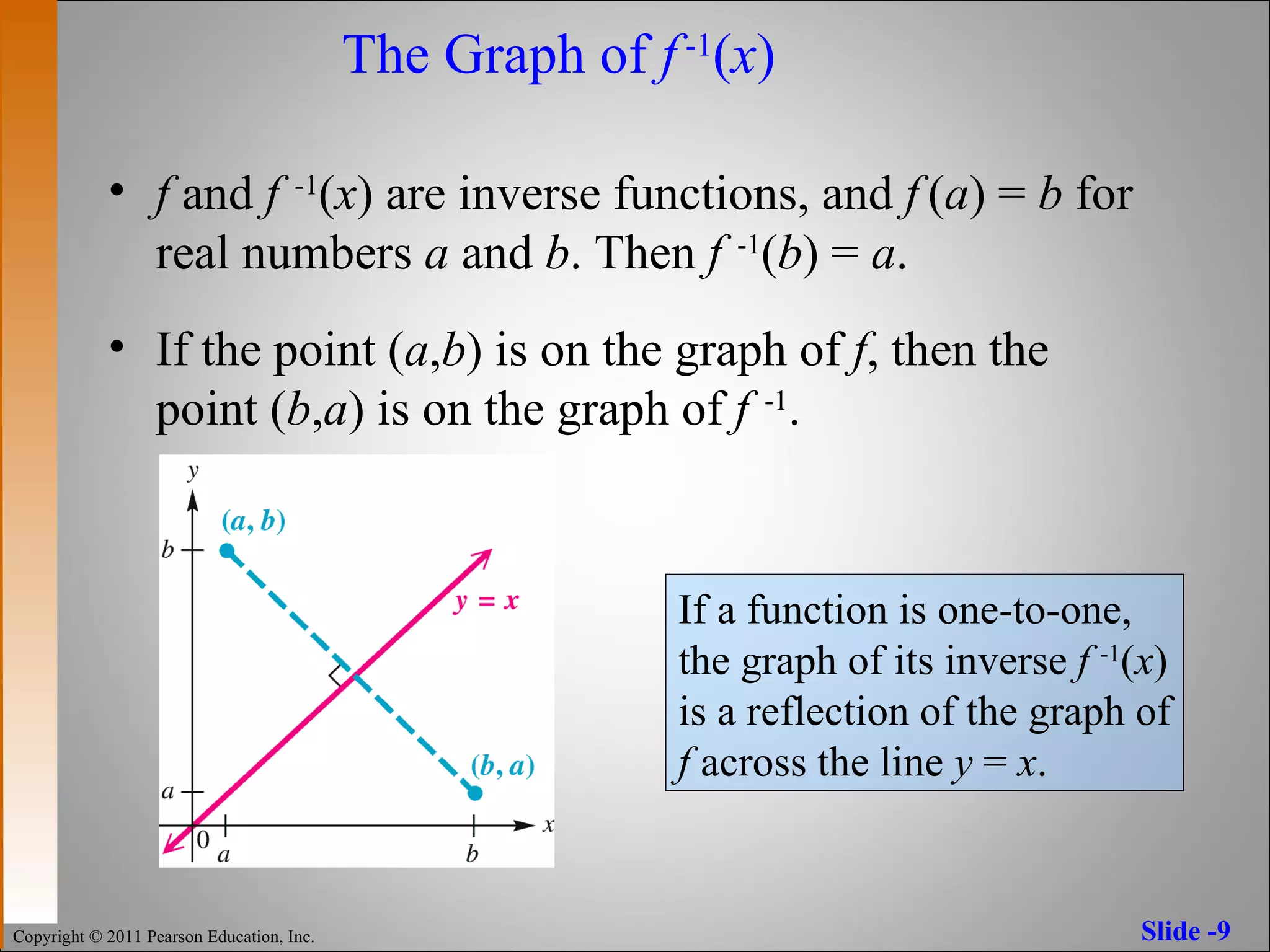
The document discusses inverse functions and one-to-one functions. It provides examples of inverse functions, explains how to determine if a function is one-to-one, and how to find the inverse of a one-to-one function. It also describes properties of inverse functions, including that the domain of a function is the range of its inverse and their graphs are reflections across the line y=x.

1. CHAPTER 6 INVERSES & ONE-to-ONE Functions

2. Inverse Functions Example Also, f [ g (12)] = 12. For these functions, it can be shown that for any value of x . These functions are inverse functions of each other.

3. Only functions that are one-to-one have inverses. One-to-One Functions A function f is a one-to-one function if, for elements a and b from the domain of f , a  b implies f ( a )  f ( b ).

4. One-to-One Functions Example Decide whether each function is one-to-one. (a) (b) Solution (a) For this function, two different x -values produce two different y -values. (b) If we choose a = 3 and b = –3, then 3  –3, but

5. Horizontal Line Test Example Use the horizontal line test to determine whether the graphs are graphs of one-to-one functions. (a) (b) If every horizontal line intersects the graph of a function at no more than one point, then the function is one-to-one. Not one-to-one One-to-one

6. Inverse Functions Example are inverse functions of each other. Let f be a one-to-one function. Then, g is the inverse function of f and f is the inverse of g if

7. Finding an Equation for the Inverse Function . Finding the Equation of the Inverse of y = f ( x ) For a one-to-one function f defined by an equation y = f ( x ) , find the defining equation of the inverse as follows. ( Any restrictions on x and y should be considered.) 1. Interchange x and y. 2. Solve for y. 3 . Replace y with f -1 ( x ).

8. Example of Finding f -1 ( x ) Example Find the inverse, if it exists, of Solution Write f ( x ) = y . Interchange x and y . Solve for y . Replace y with f -1 ( x ).

9. The Graph of f -1 ( x ) f and f -1 ( x ) are inverse functions, and f ( a ) = b for real numbers a and b . Then f -1 ( b ) = a . If the point ( a , b ) is on the graph of f , then the point ( b , a ) is on the graph of f -1 . If a function is one-to-one, the graph of its inverse f -1 ( x ) is a reflection of the graph of f across the line y = x .

10. Finding the Inverse of a Function with a Restricted Domain Example Let Solution Notice that the domain of f is restricted to [ – 5,  ), and its range is [0,  ). It is one-to-one and thus has an inverse. The range of f is the domain of f -1 , so its inverse is

11. Important Facts About Inverses If f is one-to-one, then f -1 exists. The domain of f is the range of f -1 , and the range of f is the domain of f -1 . If the point ( a , b ) is on the graph of f , then the point ( b , a ) is on the graph of f -1 , so the graphs of f and f -1 are reflections of each other across the line y = x .

12. Application of Inverse Functions Example Use the one-to-one function f ( x ) = 3 x + 1 and the numerical values in the table to code the message BE VERY CAREFUL. A 1 F 6 K 11 P 16 U 21 B 2 G 7 L 12 Q 17 V 22 C 3 H 8 M 13 R 18 W 23 D 4 I 9 N 14 S 19 X 24 E 5 J 10 O 15 T 20 Y 25 Z 26 Solution BE VERY CAREFUL would be encoded as 7 16 67 16 55 76 10 4 55 16 19 64 37 because B corresponds to 2, and f (2) = 3(2) + 1 = 7, and so on.