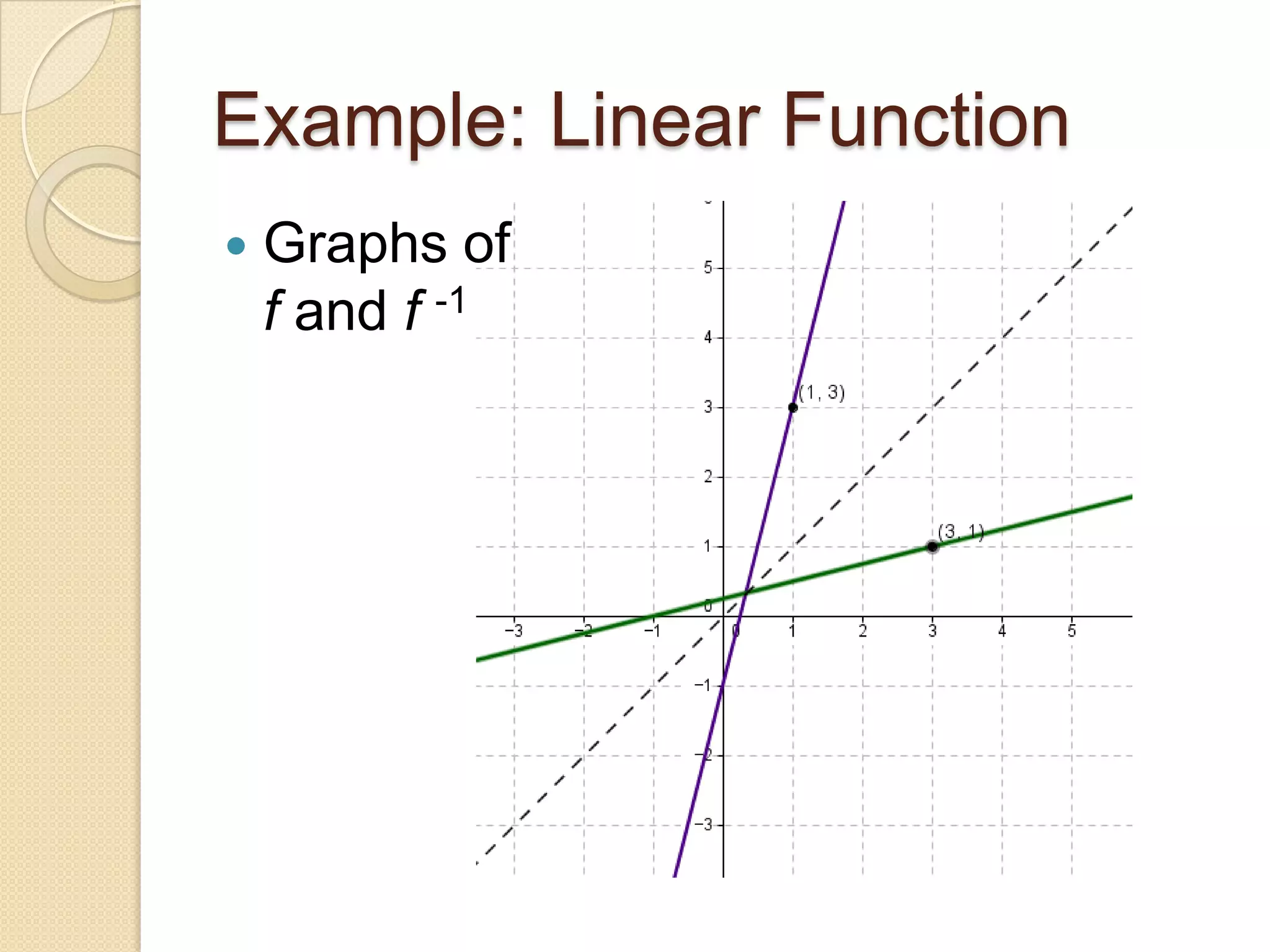
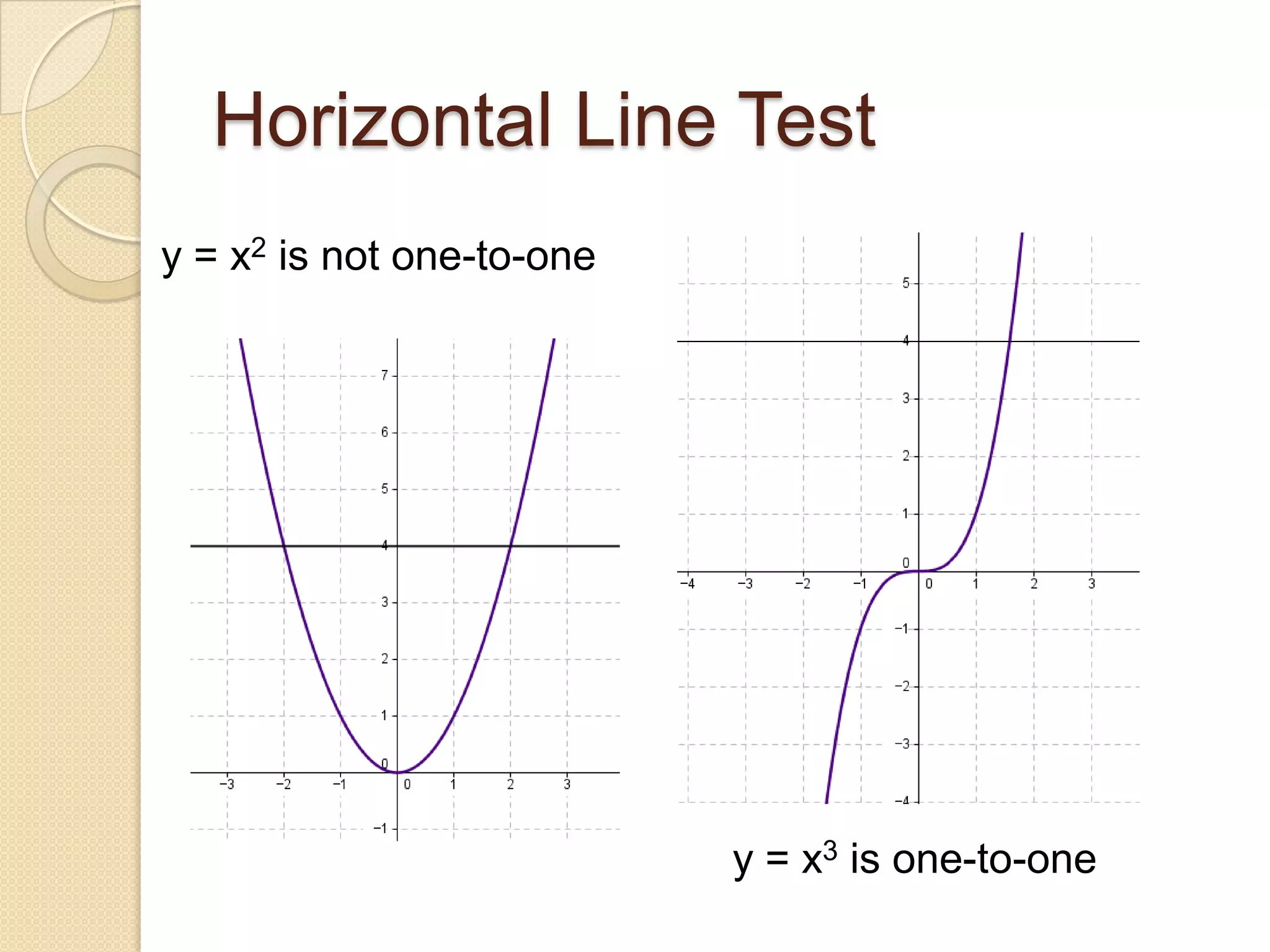
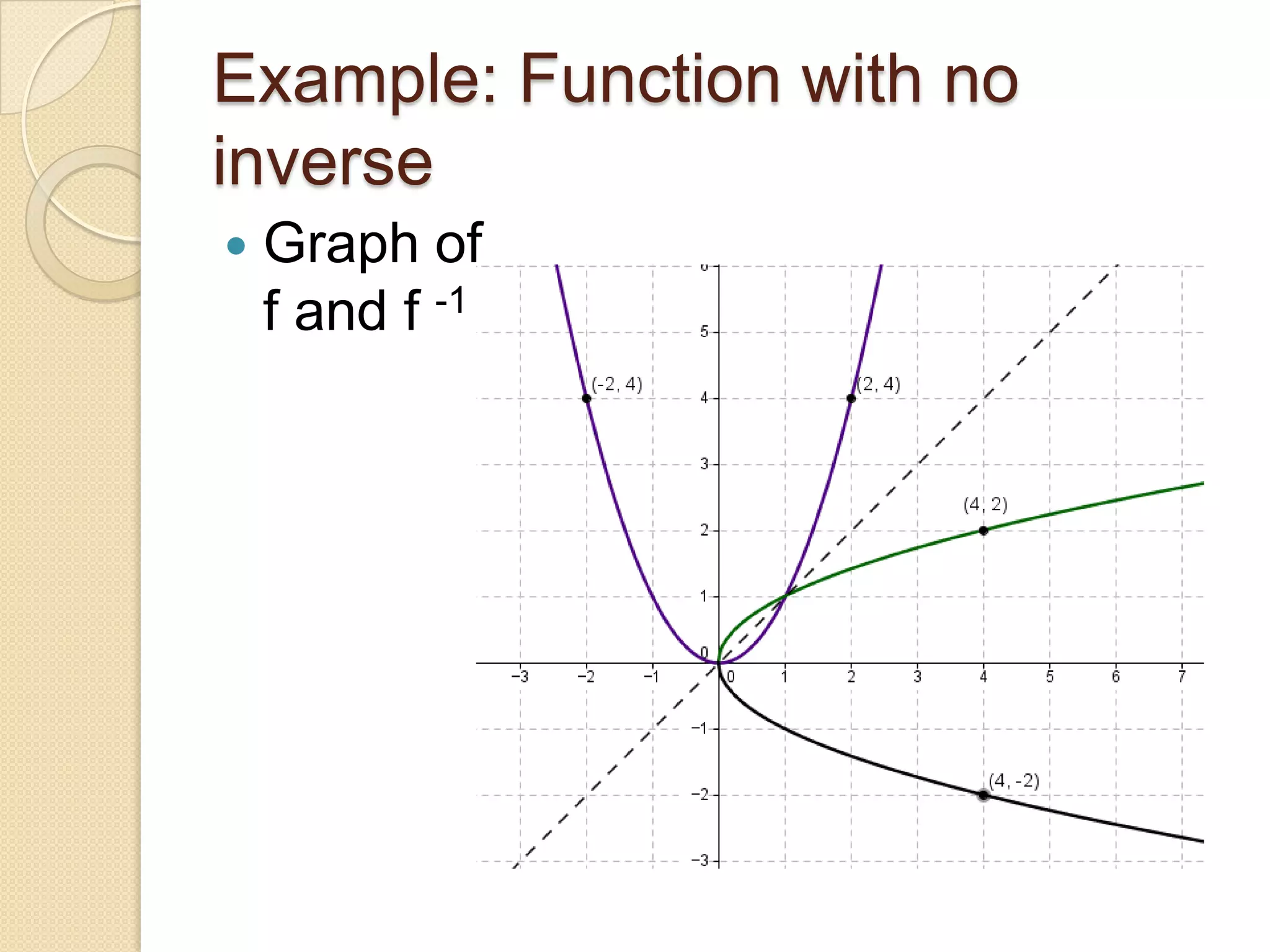
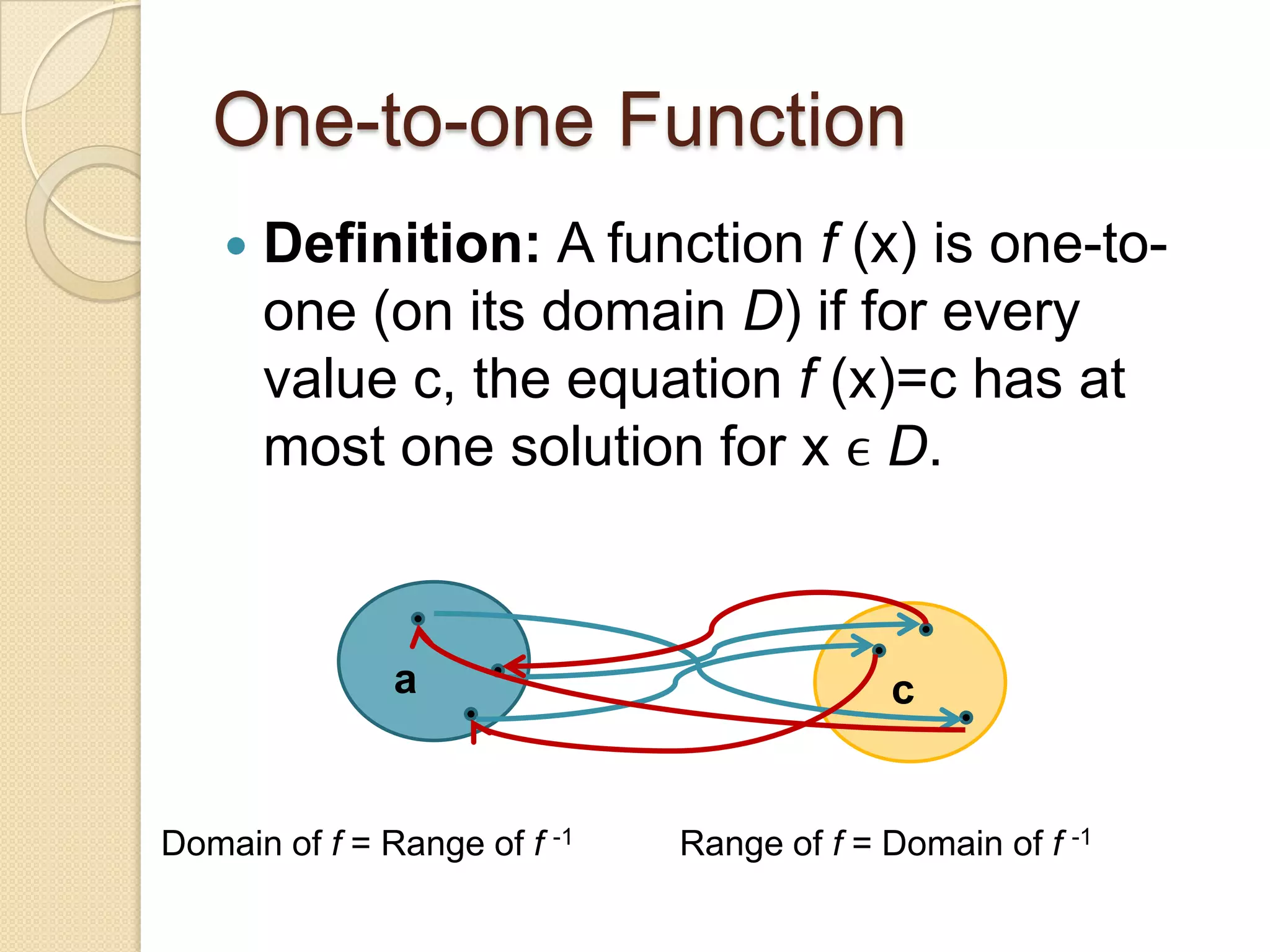
The document defines inverse functions and provides examples. An inverse function f-1(x) undoes the original function f(x) so that f-1(f(x)) = x. For a function to have an inverse, it must be one-to-one meaning each output of f(x) corresponds to only one input x. The document gives examples of linear functions that are invertible and the function y=x2 that is not invertible because it is not one-to-one. It also states that if a function f(x) is one-to-one on its domain, then it has an inverse function and the domain of f(x) is equal to the range of the

1. Inverse Functions
AP Calculus

2. Definition
 Let f (x) have domain D and range R.
The inverse function f -1 (x) (if it exists)
is the function with domain R such that
 f -1 (f (x)) = x for x ϵ D
 f (f -1 (x)) = x for x ϵ R
 If f -1 exists then f is called invertible.

3. Example: Linear Function
 Let f (x) = 4x – 1. Find f -1 (x) and show
that
f (x) is invertible.
 f -1 (x) = ¼ (x + 1)
x f (x) x f -1 (x)
0 -1 -1 0
2 7 7 2
-2 -9 -9 -2
3 11 11 3
171 683 683 171

4. Example: Linear Function
 Graphs of
f and f -1

5. Horizontal Line Test
y = x2 is not one-to-one
y = x3 is one-to-one

6. Example: Function with no
Inverse
 y = x2
 Is y = √x the inverse??
 Is y = ±√x the inverse?
x y = x2 x y = √x x y = ±√x
-2 4 4 2 4 ±2
-1 1 1 1 1 ±1
0 0 0 0 0 0
1 1 1 1 1 ±1
2 4 4 2 4 ±2

7. Example: Function with no
inverse
 Graph of
f and f -1

8. One-to-one Function
 Definition: A function f (x) is one-to-
one (on its domain D) if for every
value c, the equation f (x)=c has at
most one solution for x ϵ D.
a c
Domain of f = Range of f -1 Range of f = Domain of f -1

9. Theorem 1: Existence of
Inverses
 If f (x) is one-to-one on its domain D
then f is invertible.
 Domain of f = range of f -1
 Range of f = domain of f -1

10. Derivative of the Inverse
 Assume f (x) is invertible and one-to-
one with the inverse
g (x) = f -1 (x). If b belongs to the
domain of g (x) and f ’ (g (b)) ≠ 0 then
g ’ (b) exists and: