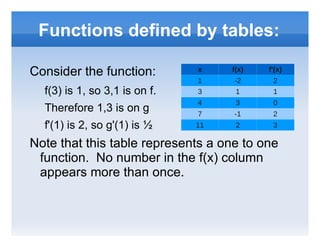
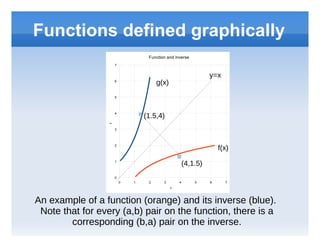
The document discusses derivatives of functions and inverse functions. It defines a function and inverse function, and explains that a function must be one-to-one to have an inverse. It also states that the slope of the tangent line to the inverse function at a point (a,b) is the inverse of the slope of the tangent line to the original function at the same point (b,a).

1. Derivatives of Functions and Inverse Functions E. Alexander Burt Potomac School

2. Review of Functions A function is a rule which maps one set of numbers (the domain) to another set of numbers (the range) The function may take the form of an equation:

3. y=f(x)

4. The function may also take the form of a set of equations

5. The function may also take the form of a table of values.

6. One to One functions In math-speak, for every value c, the function has at most one solution f(x) = c In plain English: if y=f(x) the function never produces the same y value twice. As examples, try graphing the following functions

7. y=3 x

8. y=5x-2

9. Functions which are not One to One Many functions are not one to one functions. For example, graph the following:

10. y=x 2 for -2<x<2

11. y=sin(x) for - p <x< p

12. These functions can be made into one to one functions by restricting the domain.